配送算法9 A GRASP algorithm for the Meal Delivery Routing Problem
A GRASP algorithm for the Meal Delivery Routing Problem论文学习
这篇论文聚焦哥伦比亚外卖平台的“最后一公里”配送,提出基于 GRASP 的 MDRP 求解框架:动态整合骑手可用性、订单需求与地理位置,实现订单分配与路线优化。真实数据实验表明,GRASP 在解质量与计算速度间取得有利折中,较现有仿真优化方法在订单完成率和路径效率上均具竞争。
背景
• 疫情推动外卖需求激增,哥伦比亚 Domicilios.com 2019–2020 订单量增长 50.6%,骑手数量增 62.5% 至约 19.5 万。
• 外卖 App 作为撮合平台:连接餐厅、骑手、顾客,抽佣 8–27%,负责派单、结算与路线指派。
痛点
• 末公里配送(MDRP)需实时考虑骑手容量、餐厅出餐时间、交通方式、天气等多变量;
• 骑手收入不稳、无社保,事故风险高;需求波动、路况差进一步加剧满意度难题。
本文将 MDRP 视为动态车辆路径问题(DVRP),提出 GRASP 元启发式算法;用哥伦比亚外卖平台真实一天实例验证,算法在解质量与计算时间间取得良好平衡。
问题定位
Meal Delivery Routing Problem (MDRP) 被归到 Dynamic Vehicle Routing Problem with Pickups & Deliveries(DVRP-PD)门类,其核心是“同日达”(Same-Day Delivery, SDDRP):订单当天生成、客户未知、时间窗紧张,目标是最小化未履约单量并决定所需车辆及实时路径。

求解思路
• 动态规划:理论上精确,但随状态空间爆炸陷入维度灾难。
• Rolling Horizon:周期性滚动重优化,可处理时间依赖数据,实现实时更新。
• 强化学习/多智能体:
– 以 MDP 建模订单-骑手交互,利用 RL 为每位骑手生成个性化推荐策略;
– 深度 RL 结合启发式,用于车队+无人机混合配送,无人机 FIFO 优先,车辆按插入成本派单。
关键现实约束
• 出餐时间随机:文献普遍将其视为随机变量,并用图论+数学规划+仿真一体化处理。
• 骑手冲突:多骑手抢同一订单、位置实时变化,导致决策空间连续收缩。
• 骑手福利:现有分配算法常忽视骑手自主权,最新研究呼吁在优化目标中加入“骑手自由度”指标。
计算框架
一套 Python-Docker-SimPy-OSRM 的模块化平台被提出:
① 载入真实数据校准仿真;② 定义主体交互与 KPI;③ 调用优化/路由服务输出策略。
结论:SDDRP 从早期滚动时域+启发式,正快速转向“强化学习-推荐 + 多模态运力 + 骑手福祉”的综合研究方向。
数据
• 用户 U:每个用户 u∈U 有收货地点 lu,下单时间 αo,并期望在承诺时间窗内收到餐品。
• 餐厅 R:每个餐厅 r∈R 有取货地点 lr,餐品就绪时间 eo,取餐服务时间 sr。
• 订单 O:每单 o∈O 唯一对应 (餐厅 ro, 用户 uo),并携带上述时间参数及用户收货服务时间 su。
• 骑手 C:每位骑手 c∈C 有上线时间 ec、下线时间 lc(lc>ec)、初始位置 lc(上线地点)。骑手最大同时携带订单数 ≤3。
• 酬劳:骑手每单收入由固定基价+与接单用时相关的浮动金额组成。
决策任务
任务一:订单指派
– 为每单 o∈O 选择一名骑手 co∈C,或留空(未指派)。
– 指派需实时完成,订单信息仅在骑手点击“接单”时才对其可见。
任务二:路线构建
– 对每位被指派的骑手,生成一条或多条“取-送”路线。
– 路线必须满足:
· 容量:骑手在任何时刻携带订单数 ≤3;
· 同一餐厅的多单可一次取货,形成 bundle(路线 s∈S,|餐厅|=1,|用户|≥1);
· 时间窗:取货 ≥ 餐品就绪时间 eo,送达 ≤ 承诺时间窗;
· 顺序:先取后送,单内不可交叉。

动态元素
• 平台根据实时需求滚动调整服务半径,保证用户可下单。
• 骑手位置、订单池、餐品就绪时间每秒都可能变化,需实时重算。
性能指标
• 履约单数(已指派且按时完成)。
• 平均/总送达时长(用户下单至收货)。
• 骑手利用率与收入。
求解目标
在满足容量、时间窗及实时信息更新条件下,最大化履约单量并最小化平均/总送达时长。
GRASP(Greedy Randomized Adaptive Search Procedure)完整方法
• 两阶段循环:
① Construction:随机-贪心生成初始派单方案;
② Local Search:交换订单在两骑手间的归属,缩短总行驶时间。
• 关键超参数:α(随机度)、iterations(总迭代次数)。
构造阶段(Algorithm 1)
输入:骑手集合、订单集合、α
步骤:
- 维护待派单队列 orders_pending 与可用骑手队列 couriers_available。
- 对每个骑手-订单对计算行驶时间 time_travel = 距离 / 骑手速度。
- 按 time_travel 升序排序,生成候选列表 RCL = 前 α·|列表| 个最小值。
- 从 RCL 随机选一对(骑手,订单);若骑手首次被选中,记录对应餐厅;把订单加入该骑手路线,并从待派单队列删除。
- 循环直至所有订单被指派。
输出:initial_assign(每位骑手携带的订单序列)。
局部改进阶段(Algorithm 2)
输入:initial_assign
步骤:
- 计算当前方案总行驶时间 total_time。
- 对所有不同骑手对 (c₁, c₂) 遍历:
– 对 c₁ 除首单外的任一订单 o₁,与 c₂ 除首单外的任一订单 o₂,尝试交换。
– 生成新方案 new_assign,重新计算 total_time_new。
– 若 total_time_new < total_time,则接受并更新最优方案。 - 穷尽所有可行交换后返回 better_assign。
主循环(Algorithm 3)
重复 iterations 次:
• 运行构造阶段 → 局部改进阶段 → 计算当前成本。
• 若优于历史最佳,则更新 best_solution 与 best_cost。
最终输出全局最优派单-路线方案。
运行约束(Delivery Assumptions)
• 每单有固定准备+取送时间窗,超时即视为未履约。
• 骑手最多同时携带 3 单且必须来自同一餐厅。
• 车型速度:摩托 20 km/h > 汽车 15 km/h > 自行车 12 km/h > 步行 5 km/h。
• 骑手送完最后一单后返回原地等待新任务。
实验结果
数据与平台
• 22 组真实哥伦比亚外卖日数据(订单 295–56 420 单,骑手 396–16 710 名)。
• 平台现行策略:每 2 min 重新跑派单/路径算法,目标减少排队、提高履约。

GRASP 调参
• α 0–1 步长 0.1,迭代 500–2000。
• 最优 α ≥ 0.7,迭代 ≈ 2000 时目标值最佳,但耗时 > 5 min;
• 折中选择 α = 0.7、迭代 1000:目标值仅低 2%,但耗时 < 2 min,满足业务窗口。

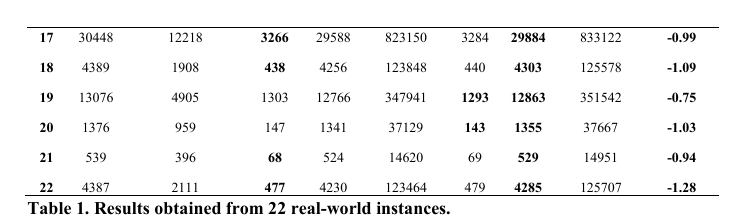
与基准对比
• GRASP 在 22 例中 21 例完成单量 ≥ 仿真优化,平均提升 0.97%,最高 1.54%。
• 路由时间略增(≤1.28%),因 GRASP 利用更多骑手(平均多用 1–3 名),换取更高履约率。
• 关键发现:GRASP 在高单量、高骑手场景下依旧稳定,展示良好可扩展性。

局限与展望
• 当前目标侧重订单完成率与行驶时间,未来需:
– 引入多目标模型,显式最大化骑手福利(收入、自由度、安全);
– 实现“配送民主化”,确保“用户-商家-骑手”三方长期可持续共赢。
