当前位置：首页 > news >正文

leetcode-hot-100 (技巧)

news 2025/8/8 6:23:59

1 . 只出现一次的数字

题目链接：只出现一次的数字
题目描述：给你一个非空整数数组 nums ，除了某个元素只出现一次以外，其余每个元素均出现两次。找出那个只出现了一次的元素。

你必须设计并实现线性时间复杂度的算法来解决此问题，且该算法只使用常量额外空间。

解答

方法一：哈希映射

直接对数组进行一次遍历，使用哈希表，对数组中的元素进行计数统计，然后再次遍历，找到计数为1（也就是只出现一次）的元素，直接返回即可。于是代码编写如下：

class Solution {
public:int singleNumber(vector<int>& nums) {unordered_map<int, int> hash;for (int num : nums) {hash[num]++;}for (int num : nums) {if (hash[num] == 1)return num;}return -1;}
};

方法二：位运算

这才是真正这道题目想要考察的知识点，可以我还是不咋会，感觉就是为了这点醋才包的这盘饺子。
对于这道题，可使用异或运算 $\oplus$ 。异或运算有以下三个性质。

$1$ .任何数和 $0$ 做异或运算，结果仍然是原来的数，即 $a \oplus 0 = a$ 。
$2$ .任何数和其自身做异或运算，结果是 0，即 $a \oplus a = 0$ 。
$3$ .异或运算满足交换律和结合律，即 $a \oplus b \oplus a = b \oplus a \oplus a = b \oplus (a \oplus a) = b \oplus 0 = b$ 。

上述位运算的数学性质知道了，这道题目就非常的简单了。代码编写如下：

class Solution
{
public:int singleNumber(vector<int> &nums){int m = 0;for (int i : nums){m = m ^ i;}return m;}
};

2 . 多数元素

题目链接：多数元素
题目描述：给定一个大小为 n 的数组 nums ，返回其中的多数元素。多数元素是指在数组中出现次数大于 $⌊ n /2 ⌋$ 的元素。

你可以假设数组是非空的，并且给定的数组总是存在多数元素。

解答

方法一：排序

直接调用 $sor t$ , 然后由于多数元素数量肯定大于 $⌊ n /2 ⌋$ ，因此直接取排序后中间位置的数字即可。

class Solution
{
public:int majorityElement(vector<int> &nums){sort(nums.begin(), nums.end()); // 排序原数组return nums[nums.size() / 2];  // 取中间的位置}
};

方法二：哈希表

使用哈希映射（ $H a s h M a p$ ）来存储每个元素以及出现的次数。对于哈希映射中的每个键值对，键表示一个元素，值表示该元素出现的次数。然后找到哈希表中最大的那个值对应的数字即可。

class Solution {
public:int majorityElement(vector<int>& nums) {unordered_map<int, int> counts;int majority = 0, cnt = 0;for (int num: nums) {++counts[num];if (counts[num] > cnt) {majority = num;cnt = counts[num];}}return majority; // 返回出现次数最多的那个值}
};

方法三：Boyer-Moore 投票算法

把众数（对应该题目的多数元素）记为 +1，把其他数记为 −1，将它们全部加起来，显然和大于 0，从结果本身也可以看出众数比其他数多。

class Solution {
public:int majorityElement(vector<int>& nums) {int x = 0, votes = 0;for (int num : nums){if (votes == 0) x = num; // 重新选择众数，保证 votes 非负votes += num == x ? 1 : -1; // 等于 x ，认为是众数，直接票数直接加 1 ，其它的数字都减 1 。}return x;}
};

还有一些其他的方法，如分治，随机化等，详细解释过程参见：官方解答

3 . 颜色分类

题目链接：颜色分类
题目描述：给定一个包含红色、白色和蓝色、共 n 个元素的数组 nums ，原地对它们进行排序，使得相同颜色的元素相邻，并按照红色、白色、蓝色顺序排列。

我们使用整数 0、 1 和 2 分别表示红色、白色和蓝色。

必须在不使用库内置的 sort 函数的情况下解决这个问题。

解答

方法一：三指针法

可以使用三个指针来维护数组的四个区域

[0, low)     →   所有 0（红色）
[low, mid)   →   所有 1（白色）
[mid, high]  →   待处理区域
(high, n-1]  →   所有 2（蓝色）

上述：

$l o w$ ：下一个 0 应该放的位置（初始为 $0$ ）
$mi d$ ：当前正在处理的元素（初始为 $0$ ）
$hi g h$ ：下一个 2 应该放的位置（初始为 $n - 1$ ）
用 $mi d$ 遍历数组，根据 $n u m s [mi d]$ 的值进行交换和指针移动。

class Solution {
public:void sortColors(vector<int>& nums) {int low = 0;        // 0 的右边界int mid = 0;        // 当前处理位置int high = nums.size() - 1;  // 2 的左边界while (mid <= high) {if (nums[mid] == 0) {swap(nums[low], nums[mid]);low++;mid++;  // 此处 mid 可以++，因为 nums[low] 原来是 1 或刚处理过}else if (nums[mid] == 1) {mid++;}else { // nums[mid] == 2swap(nums[mid], nums[high]);high--;// mid 不++，因为从 high 换过来的数还没检查}}}
};

方法二：双指针 + 主扫描指针

CORE IDEA：维护两个边界指针 ptr_begin 和 ptr_end，分别表示 0 区的右边界和 2 区的左边界。用一个主循环指针 i 从左到右扫描数组，遇到 2 就交换到右边，遇到 0 就交换到左边。

class Solution
{
public:void sortColors(vector<int> &nums){int n = nums.size();int ptr_begin = 0, ptr_end = n - 1;for (int i = 0; i <= ptr_end; i++){while (i <= ptr_end && nums[i] == 2){swap(nums[i], nums[ptr_end]);ptr_end--;}if (nums[i] == 0){swap(nums[i], nums[ptr_begin]);ptr_begin++;}}}
};

上述代码的细节说明：
1、为什么 2 要用 while 循环？
因为当你把 nums[i] == 2 和 nums[ptr_end] 交换后，换回来的 nums[i] 可能还是 2（比如 ptr_end 原来也是 2），所以必须继续检查，直到 nums[i] != 2。
如果只用 if，可能会漏掉新换回来的 2。

2、为什么 0 只用 if？
因为 i 是从左往右走的，ptr_begin <= i，所以 nums[ptr_begin] 要么是 1，要么是刚处理过的 0。

当把 nums[i] == 0 和 nums[ptr_begin] 交换后：

如果 nums[ptr_begin] 是 1，换回来的是 1，i 继续前进没问题。
如果 nums[ptr_begin] 是 0，那说明 ptr_begin == i，交换后不变。

所以换回来的值不会是 2，也不需要再检查，i++ 即可。

3、为什么循环条件是 i <= ptr_end？
因为 ptr_end 是 2 区的左边界，ptr_end 右边已经全是 2 了，不需要再处理。

当 i > ptr_end 时，说明所有非 2 的元素已经处理完了。

上述两种方法区别不是很大：

特性	方法二	方法一（low/mid/high）
指针数量	3 个（`i`, `ptr_begin`, `ptr_end`）	3 个（`low`, `mid`, `high`）
处理 `2` 的方式	`while` 循环确保 `nums[i]!=2`	交换后 `mid` 不++，下次再处理
处理 `0` 的方式	`if` 判断后交换	交换后 `low++`, `mid++`
代码风格	主循环 `i++`，`2` 用 `while` 控制	`mid` 控制循环，条件分支控制移动
时间复杂度	O(n)	O(n)
空间复杂度	O(1)	O(1)

4 . 下一个排列

题目链接：下一个排列
题目描述：
给你一个整数数组 nums ，找出 nums 的下一个排列。

必须原地修改，只允许使用额外常数空间。

解答

例子：

输入：[1,2,3] → 输出：[1,3,2]
输入：[3,2,1] → 输出：[1,2,3]
输入：[1,1,5] → 输出：[1,5,1]

🧮涉及的数学知识

1. 排列（Permutation）

排列是从一组元素中按一定顺序选出所有元素的可能方式。对于 n 个不同元素，共有 n! 个排列。

例如：[1,2,3] 的所有排列为：

[1,2,3]
[1,3,2]
[2,1,3]
[2,3,1]
[3,1,2]
[3,2,1]

这些排列是按字典序（lexicographical order）排列的。

✅ 字典序：就像单词在字典中排序一样，从左到右逐位比较大小。

2. 字典序与排列的“下一个”

我们希望找到比当前排列刚好大一点的那个排列。这就需要理解：

如何判断一个排列是否是“最大的”？→ 降序排列（如 [3,2,1]）
如何生成下一个字典序排列？

🔍核心数学思想：如何找到“下一个排列”？

我们不能暴力生成所有排列，那样时间复杂度太高（O(n!)）。我们需要一个高效的构造性算法。

✅ 算法思路（基于组合数学中的“字典序生成法”）

这个算法源自 Narayana Pandita 在14世纪提出的“下一个字典序排列”算法，步骤如下：

📌 步骤详解：

假设数组为 nums，长度为 n

Step 1：从右往左找第一个“可上升”的位置 `i`

找最大的索引 i，使得 nums[i] < nums[i+1]
换句话说：从右往左找第一个“左边小于右边”的相邻对。

如果找不到这样的 i，说明整个数组是降序的，已经是最大排列 → 直接反转成最小排列（升序）即可。
否则，说明从 i 开始可以“变大”。

✅ 数学意义：i 是可以被“替换”以生成更大排列的最右位置。

Step 2：从右往左找第一个大于 `nums[i]` 的元素 `nums[j]`

找最大的索引 j，使得 j > i 且 nums[j] > nums[i]

因为从 i+1 到末尾是降序的（由 Step 1 的选择决定），所以从右往左第一个大于 nums[i] 的就是最小的、比 nums[i] 大的数。

✅ 数学意义：选择“刚好比 nums[i] 大”的数来替换，确保变化最小。

Step 3：交换 `nums[i]` 和 `nums[j]`

这一步让排列变大了，但还不够“下一个”，我们需要让后面的尽可能小。

Step 4：反转 `i+1` 到末尾的子数组

交换后，i+1 到末尾仍然是降序的。
反转它，变成升序，这样后缀最小，整体排列就是“下一个”字典序排列。

✅ 数学意义：固定前缀 0..i 后，最小的后缀排列是升序。

🧩举个例子

以 nums = [1,3,2] 为例：

从右往左找 i，使得 nums[i] < nums[i+1]
- nums[1]=3, nums[2]=2 → 3 > 2 ❌
- nums[0]=1, nums[1]=3 → 1 < 3 ✅ → i = 0
从右往左找 j，使得 nums[j] > nums[i]（即 >1）
- nums[2]=2 > 1 ✅ → j = 2
交换 nums[0] 和 nums[2] → [2,3,1]
反转 i+1 到末尾（即索引 1 到 2）：[3,1] → 反转后 [1,3]
最终结果：[2,1,3]

✅ 正确！因为 [1,3,2] 的下一个是 [2,1,3]

✅ 算法实现（Python）

def nextPermutation(nums):n = len(nums)# Step 1: 从右往左找第一个 nums[i] < nums[i+1]i = -1for idx in range(n - 2, -1, -1):if nums[idx] < nums[idx + 1]:i = idxbreak# 如果没有找到，说明是最大排列，直接反转if i == -1:nums.reverse()return# Step 2: 从右往左找第一个 nums[j] > nums[i]j = -1for idx in range(n - 1, i, -1):if nums[idx] > nums[i]:j = idxbreak# Step 3: 交换nums[i], nums[j] = nums[j], nums[i]# Step 4: 反转 i+1 到末尾left, right = i + 1, n - 1while left < right:nums[left], nums[right] = nums[right], nums[left]left += 1right -= 1

⏱️ 时间复杂度分析

Step 1: $O (n)$
Step 2: $O (n)$
Step 3: $O (1)$
Step 4: $O (n)$

✅ 总体时间复杂度： $O (n)$
✅ 空间复杂度： $O (1)$ （原地修改）

📚总结：涉及的数学知识

数学概念	在题目中的作用
排列（Permutation）	理解所有可能的顺序组合
字典序（Lexicographic Order）	定义“下一个”的标准
单调性分析	从右往左找上升点，利用后缀的降序性质
贪心思想	找最小增量的下一个排列
组合生成算法	使用 Narayana Pandita 的经典构造法

根据上述相关思路，可以写出C++代码如下：

class Solution {
public:void nextPermutation(vector<int>& nums) {int i = nums.size() - 2;while (i >= 0 && nums[i] >= nums[i + 1]) {i--;}if (i >= 0) {int j = nums.size() - 1;while (j >= 0 && nums[i] >= nums[j]) {j--;}swap(nums[i], nums[j]);}reverse(nums.begin() + i + 1, nums.end());}
};

拓展

全排列生成（利用 $n e x tP er m u t a t i o n$ 生成全排列

）
使用“下一个排列”算法可以很方便地生成给定数组的所有排列。基本思路是从最小的排列（即升序排列）开始，不断调用“下一个排列”算法，直到返回到初始排列为止。

步骤如下：

初始化：首先对数组进行排序，得到字典序中最小的排列。
循环调用：然后进入一个循环，在每次迭代中调用“下一个排列”算法，并打印或保存当前排列，直到回到初始排列（对于某些实现来说，这可能意味着再次达到最大排列后重新回到最小排列，具体取决于你的处理逻辑）。

void generateAllPermutations(std::vector<int> nums) {std::sort(nums.begin(), nums.end());// 得到字典序列中最小的排列std::vector<int> start = nums; // 设置生成排列的终止条件do {// 打印当前排列for (int num : nums) {std::cout << num << " ";}std::cout << std::endl;nextPermutation(nums);// 当再次达到起始排列时停止（说明已经循环完）} while (nums != start);
}

上一个排列

思路和 下一个排列 相似，但是比较的方向是相反的。

从右向左找第一个降序对：找到最大的索引 $i$ 使得 $n u m s [i] > n u m s [i + 1]$ 。
从右向左找第一个小于 $n u m s [i]$ 的元素：找到最大的索引 $j$ 使得 $j > i$ 并且 $n u m s [j] < n u m s [i]$ 。
交换：交换 $n u m s [i]$ 和 $n u m s [j]$ 。
反转：将 $i + 1$ 到末尾的部分反序以获得最小的字典序排列。

void prevPermutation(std::vector<int>& nums) {int n = nums.size();int i = -1;// Step 1: 从右往左找第一个 nums[i] > nums[i+1]for (int idx = n - 2; idx >= 0; idx--) {if (nums[idx] > nums[idx + 1]) {i = idx;break;}}// 如果没有找到，说明是最小排列，直接反转成最大排列if (i == -1) {std::reverse(nums.begin(), nums.end());return;}// Step 2: 从右往左找第一个 nums[j] < nums[i]int j = -1;for (int idx = n - 1; idx > i; idx--) {if (nums[idx] < nums[i]) {j = idx;break;}}// Step 3: 交换std::swap(nums[i], nums[j]);// Step 4: 反转 i+1 到末尾std::reverse(nums.begin() + i + 1, nums.end());
}

也可以使用 C++ 中提供的两个函数

#include <algorithm>
#include <vector>
#include <iostream>// 生成所有排列（推荐方式）
void generateAllPermutationsSTL(std::vector<int> nums) {std::sort(nums.begin(), nums.end());do {for (int num : nums) {std::cout << num << " ";}std::cout << std::endl;} while (std::next_permutation(nums.begin(), nums.end()));
}// 获取上一个排列（STL）
void usePrevPermutationSTL(std::vector<int>& nums) {std::prev_permutation(nums.begin(), nums.end());
}// 获取下一个排列（STL）
void usenextPermutationSTL(std::vector<int>& nums) {std::next_permutation(nums.begin(), nums.end());
}

5 . 寻找重复数

题目链接：寻找重复数
题目描述：
给定一个包含 n + 1 个整数的数组 nums ，其数字都在 [1, n] 范围内（包括 1 和 n），可知至少存在一个重复的整数。

假设 nums 只有一个重复的整数，返回这个重复的数。

你设计的解决方案必须不修改数组 nums 且只用常量级 O(1) 的额外空间。

解答

解答一：使用 C++ 中的 unordered_map 进行求解。

看到这道题目，我的第一个想法就是使用哈希映射进行求解，对于每次出现的数字，对其进行计数，判断出现的次数即可，于是这里就使用到了 C++ 中提供的 unordered_map 这个 STL 容器。代码编写如下：

class Solution {
public:int findDuplicate(vector<int>& nums) {unordered_map<int, int> count;for (int num : nums) {count[num]++;if (count[num] > 1)return num;}return -1;}
};

解答二：使用 C++ 中的 unordered_set 进行求解。

解答一中使用到的 unordered_map 在判断 “出现几次” 中有很好的作用，但是此题实际上只需要判断是否存在即可，因为要是存在，再加上当前 for 循环扫描到的位置的这个是，于是可以判断当前位置的数字就是我们需要找寻的重复数了。而 C++ 中提供的 unordered_set 就可以只判断 “是否存在” 。基于此，代码可修改如下：

class Solution {
public:int findDuplicate(vector<int>& nums) {unordered_set<int> seen;for (int num : nums) {if (seen.find(num) != seen.end()) {return num;}seen.insert(num);}return -1;}
};

下面的三种方法是官方给的标准解答，这里也详细描述一下：

官解一：二分查找 + 计数思想（抽屉原理）

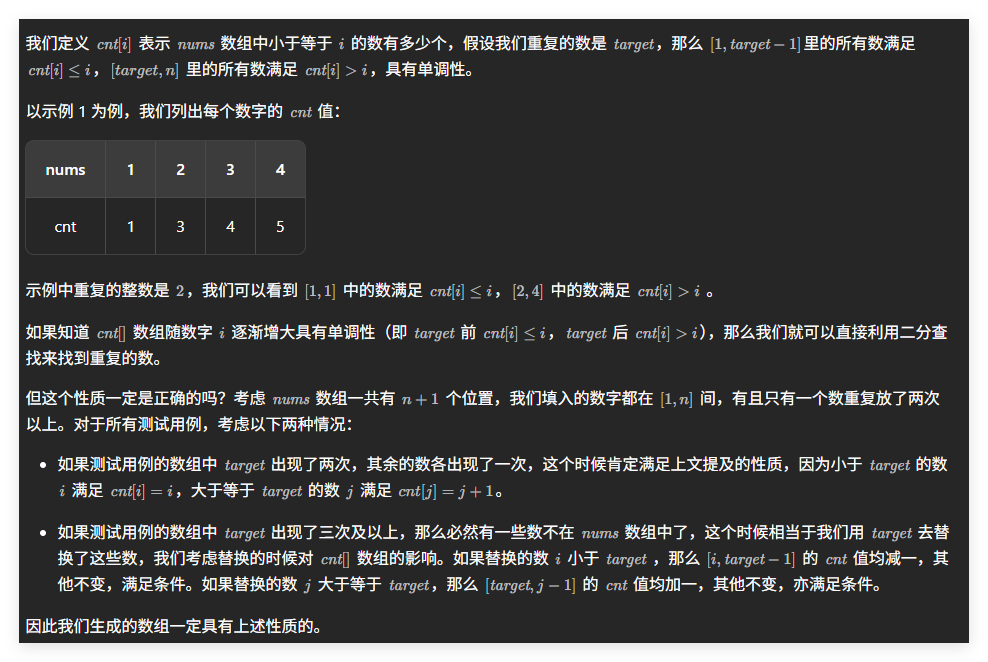
在这里插入图片描述

class Solution {
public:int findDuplicate(vector<int>& nums) {int len = nums.size();           // 数组长度为 n+1，数字范围是 [1, n]int l = 1, r = len - 1;          // 二分查找的范围：所有可能的数字 [1, n]int ans = -1;                    // 用于记录最终答案（重复的数）// 开始二分查找：我们不是在数组下标上二分，而是在【数值范围】上二分while (l <= r) {int mid = (l + r) >> 1;      // 等价于 (l + r) / 2，取中间值作为“猜测”的目标数// 我们要判断：重复的数是否 <= mid？int cnt = 0;                 // 计数器：统计数组中 <= mid 的数字个数// 遍历整个数组，统计有多少个数 <= midfor (int i = 0; i < len; i++) {if (nums[i] <= mid) {    // 如果当前数在 [1, mid] 范围内cnt++;               // 就计入总数}// 等价写法：cnt += (nums[i] <= mid);}/** 核心思想：抽屉原理（Pigeonhole Principle）** 数字范围是 [1, n]，共有 n+1 个数，至少一个重复。** 假设没有重复：*   - [1, mid] 应该恰好有 mid 个不同的数*   - 所以数组中 <= mid 的数应该正好是 mid 个** 但现在有重复：*   - 如果 cnt > mid：说明在 [1, mid] 范围内的数出现了超过 mid 次*     → 必然有重复的数落在 [1, mid] 中*   - 如果 cnt <= mid：说明 [1, mid] 范围内的数没有“超额”，重复的数一定在 (mid, n] 中*/if (cnt <= mid) {// [1, mid] 范围内的数没有超额，重复数不在这里// 所以答案在右半部分：(mid, r]l = mid + 1;} else {// [1, mid] 范围内的数“太多”了（超过 mid 个）// 说明重复的数一定在 [1, mid] 中r = mid - 1;ans = mid;  // 更新答案：mid 是一个可能的重复数（但我们还要继续缩小范围）// 注意：这里 ans = mid 只是记录当前满足条件的值// 最终 ans 会收敛到最小的那个满足 cnt > mid 的 mid 值，// 也就是重复的数。}}return ans;  // 返回最终找到的重复数字}
};

官解二：快慢指针

详细的解释看官方解答

我这里只是大致的描述一下其算法流程：

第一阶段用 “两倍速度” → 得到一个相遇点
然后用数学推导 → 得到一个重要等式 $a = k L - b$
第二阶段不管速度了，只靠这个等式 → 让两个同速指针在入口相遇

阶段	速度设置	目的	是否使用“两倍关系”
$P ha se 1$	快=2×慢	找到相遇点，推导 $a = k L - b$	✅ 是（用于推导）
$P ha se 2$	快=慢=1步	利用 $a = k L - b$ 找入口	❌ 否（只用结论，不用速度）

详细的过程还是需要参考官解。主要是需要了解一下 $Fl oy d$ 判圈算法。

class Solution {
public:int findDuplicate(vector<int>& nums) {int slow = 0, fast = 0;// Phase 1: 找到快慢指针相遇点（证明环存在）do {slow = nums[slow];        // 慢指针走一步：slow → nums[slow]fast = nums[nums[fast]];  // 快指针走两步：fast → nums[nums[fast]]} while (slow != fast);       // 直到两者相遇// 此时 slow == fast，位于环中某一点（不一定是入口）// Phase 2: 找环的入口（即重复的数）slow = 0;  // 将慢指针重新放回起点 0while (slow != fast) {slow = nums[slow];  // 两个指针都每次走一步fast = nums[fast];}// 当它们再次相遇时，就是环的入口！return slow;  // 返回入口节点的值（注意：此时 slow 是索引，但它的“含义”是答案）}
};