C语言(08)——整数浮点数在内存中的存储
在详细认识整型在内存中的存储方式前,可以在下文中阅读他们的底层逻辑:
C语言(07)——原码 补码 反码 (超绝详细解释)_c语言 求补码-CSDN博客
摘要:本文详细介绍了C语言中整型和浮点数在内存中的存储方式。整型采用补码形式存储,分为原码、反码和补码三种表示方法。内存存储涉及大小端字节序问题,大端模式将高位存储在低地址,小端模式相反。浮点数按IEEE754标准存储,由符号位(S)、指数位(E)和有效数字(M)组成,其中指数E采用偏移值存储。文章还详细说明了不同情况下E的取值规则,包括正常情况、全0和全1时的特殊处理。这些底层存储机制直接影响程序的数据处理和跨平台兼容性。
目录
1. 整数的内存存储
1.1 大小端字节序存储
2. 浮点数的内存存储
2.1 浮点数定义
2.2 浮点数的存储
2.2.1 指数E在内存中的存取
1. 整数的内存存储
整数的二进制表现方式有三种:原码、反码、补码;
在计算器中,整数的数据存放是以补码的形式进行存储的;
有符号的整数,三种表示方法均有符号位和数值位两部分,符号位都是用0表示“正”,用1表示“负”,最高位的一位是被当做符号位,剩余的都是数值位。
注:正整数的原、反、补码都相同;负整数的三种表示方法各不相同。
三种表示方法他们之间的转换如下图所示:
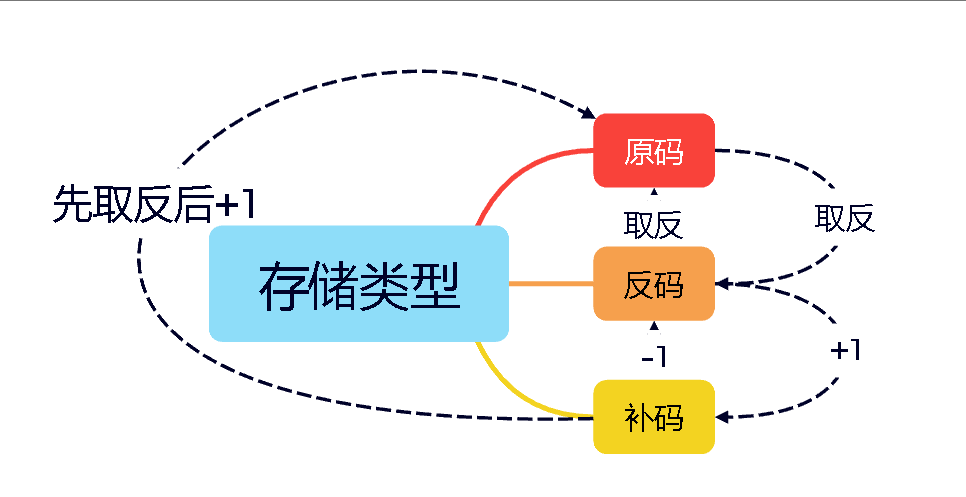
1.1 大小端字节序存储
我们思考这么一个问题:一个整型在内存中需要使用4个字节,那么这四个字节里的内容分别是怎么分布的呢?以下图为例,VS编译器对整型a(0x11223344)的数据内容是如何存放的呢?11223344?44332211?还是其他更为复杂的方式如22113344?
在对超过一个字节的数据进行内存存储时,就会出现如上所示的存储顺序的问题,按照不同的存储顺序,我们可以分为大端字节序存储和小端字节序存储,下面是具体的概念:
大端(存储)模式:
是指数据的低位字节内容保存在内存的高地址处,而数据的高位字节内容,保存在内存的低地址处;
小端(存储)模式:
是指数据的低位字节内容保存在内存的低地址处,而数据的高位字节内容,保存在内存的高地址处。
数据中的低位和高位类似于十进制中“高位数字”和“低位数字”的含义(如十进制数1234中,1是高位,4是低位),高位和低位可以用不同进制中的权重来理解。
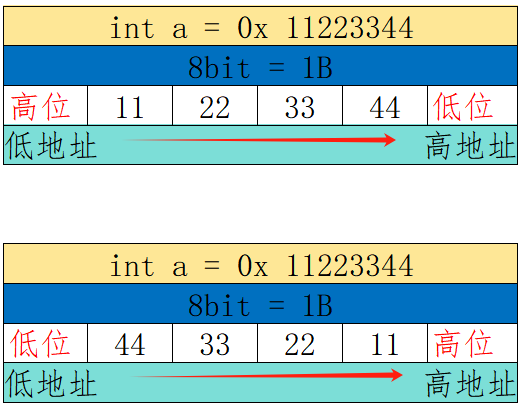
注:字节序是计算机系统中对多字节数据的通用存储规则,与内存区域(栈、堆、全局区等)无关,只要涉及多字节数据的存储或传输,就会受到字节序的影响。
大小端字节序的选择主要取决于处理器(CPU)的架构设计
2. 浮点数的内存存储
2.1 浮点数定义
常见的浮点数有:3.14、2E12等,浮点数家族包括:float、double、long double类型,浮点数表示的范围在float.h定义,在C语言中输入的浮点数会默认识别为double类型,如需声明float,则需在数字后加上f。
2.2 浮点数的存储
根据国际标准IEEE(电气和电子工程协会)754,任意一个二进制浮点数V可表示成下面的形式:
V = (-1)* S M * 2E
(-1)*S表示符号位,当S=0时,V为正数;当S=1,V为负数;
M表示有效数字,M值大于等于1,小于2(根据这个特性,知道M的整数为恒为1,故内存中对M的存储均为小数点数据);
2^E表示指数位。
举例来说:
浮点数121.36转换为科学计数法的形式为1.2136E2,那么按照上面的形式我们可以得到:S=1,M=1.2136,E=2。
IEEE 754 规定:
对于32位的浮点数,最高的1位存储符号位S,接着的8位存储指数E,剩下的23位存储有效数字M
对于64位的浮点数,最高的1位存储符号位S,接着的11位存储指数E,剩下的52位存储有效数字M

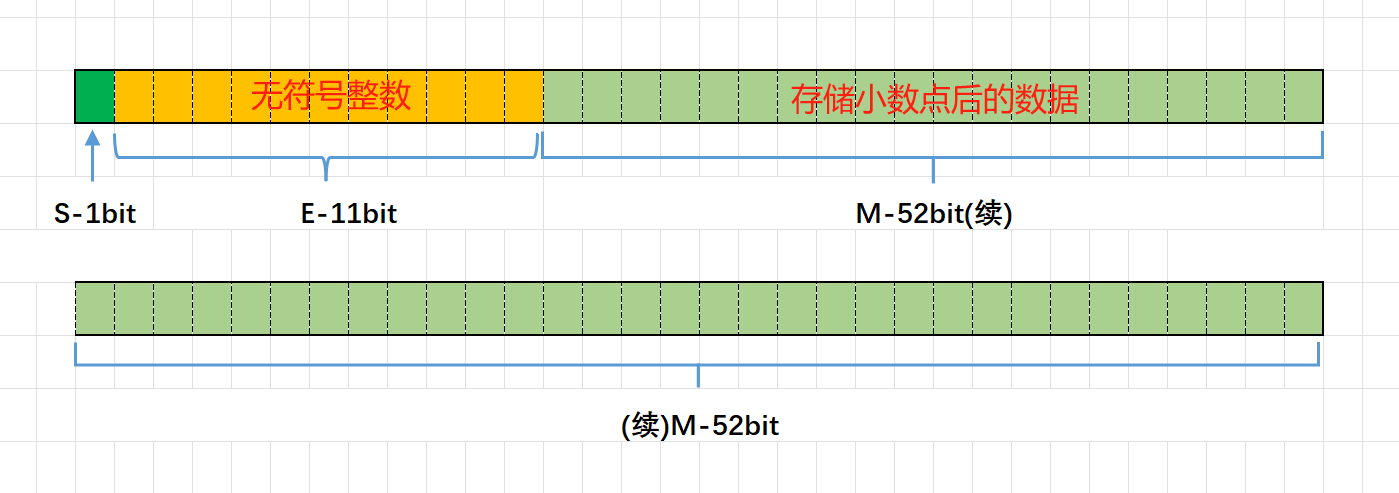
2.2.1 指数E在内存中的存取
指数E为一个无符号整数(unsigned int)
当E为8位时,他的取值范围为0~255;E为11位时,他的取值范围为0~2047。
在科学计数法中我们知道E是存在负数的情况,因此IEEE 754规定,存入内存时E的真实值必须再加上一个中间数,对于8位的E,中间数为127;对于11位的E,中间数为1023。如,1.2136E2中的E为2,那么在保存为32为浮点数时,E需变成2+127=129,即1000 0001。
指数E从内存中取出时分为三种情况:
E不全为0或不全为1(正常情况):
在这种情况下,E遵循上述的规则,只需把他的计算值-127(或-1023)即可,同时不要忘记在求得的M值前加上1.
E全为0:
当所有位都为0时,其真实指数是固定值,单精度浮点数的真实指数为1-127=-126,双精度浮点数的真实指数为1-1023=-1022(为非格式化数),此时有效数字M不再加上第一位的1.,而是还原成0.xxxxxx的小数。这样做是为了表示±0,以及接近于0的很小的数字。
E全为1:
IEEE 754规定,如果此时M为0,则表示±无穷大(正负位取决于S)。
如果M不为0,此时不是无穷大,而是非数NaN,用来表示无效运算结果。
