当前位置：首页 > news >正文

KMP-next数组详解

news 2025/8/9 23:28:03

KMP核心

核心是next数组，其本质上是基于模式串的可见性，操作模式串得出的

举一个简单例子：

序号/下标	1	2	3	4	5	...
主串	a	b	a	b	？	...
模式串	a	b	a	b	c	...
next[i]	0	1	1	2	3	...

可以看到，在下标5的位置失配，肉眼可见，模式串应该从3的位置开始和主串的5位置开始比较

因为前面两个ab元素能够匹配上，无需再次验证

这便是next数组需要做的：提前标明哪个位置失配时，模式串指针应该从哪个位置开始和主串比较

整个过程，主串的指针是不回溯的，也就是不会返回，一直向前，这也是不同于朴素算法的关键

next数组

我们肉眼当然能很快知道失配时应该从哪个位置重新开始，但计算机不知道，所以需要设计next[]数组

对 next[i] 理解可以有以下两种：

当模式串中第 i 位置(i=1除外)的字符失配时，模式串指针应该回到哪个位置继续和主串原失配位置比较
next[i]表示的值为：长度为i-1的子串的最长公共前后缀+1

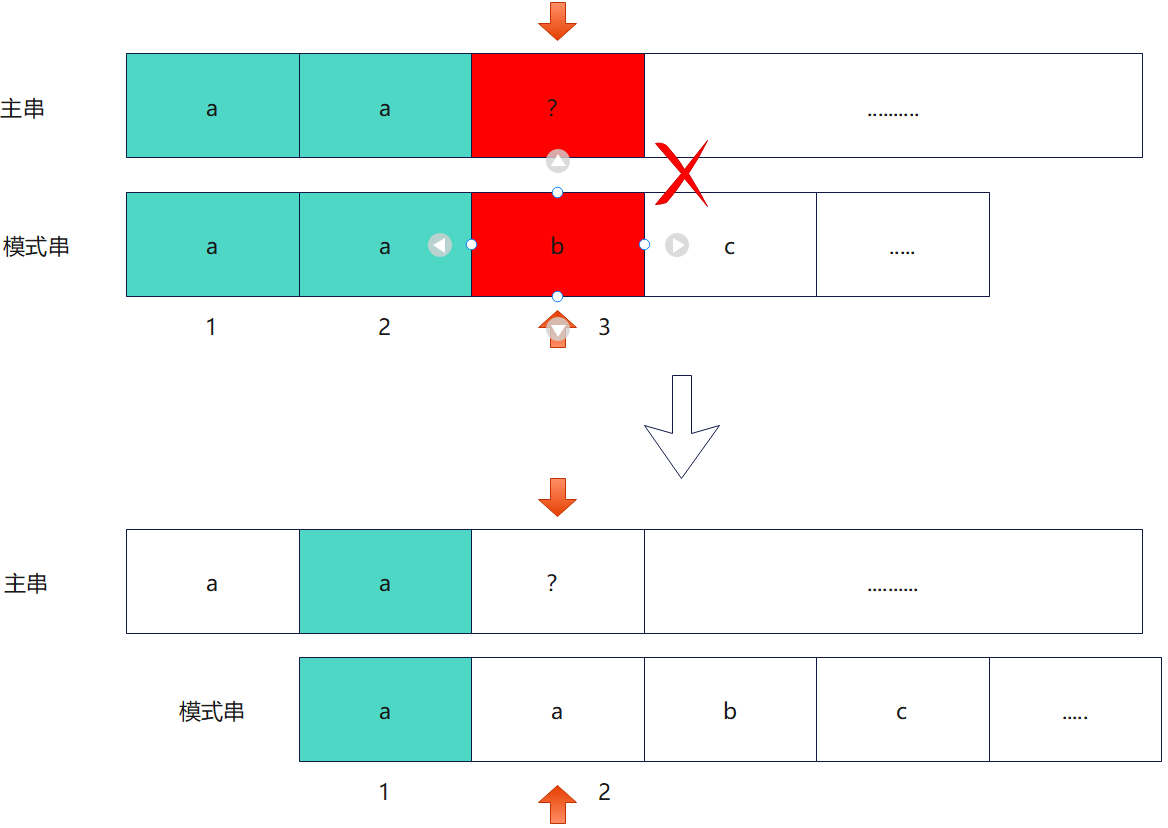
对于第二种理解：结合第一种理解，以"b"为例，b元素前的子串为"aa"，可以知道，最长公共前后缀为1，当"b"失配时，指针指向的是2，也就是next[2] = 2；即跳过了最长公共前后缀的部分(1+1)，因为那是已知的、最长的、无需再次匹配的有效子串

序号/下标	1	2	3	4	5	6	7	8
模式串	a	a	b	c	a	a	a	a
next[i]	0	1	2	1	1	2	3	3

根据以上的例子，我们分别以两种方式来解释一下：

next[1]=0：特殊情况，固定值，模式串在第1个元素就失配，主串跟模式串的指针都要++

next[2]=1：特殊情况，固定值，模式串在第2个元素失配，模式串指针回到第一个位置重配

next[3]=2：在第3个元素失配，模式串指针回到第2个元素重配；子串"aa"的最长公共前后缀为1

next[4]=1：第4个元素失配，模式串指针回到第1个元素重配，子串"aab"最长公共前后缀为0

next[5]=1：第5个元素失配，模式串指针回到第1个元素重配，子串"aabc"最长公共前后缀为0

next[6]=2：第6个元素失配，模式串指针回到第2个元素重配，子串"aabca"最长公共前后缀为1

next[7]=3：第7个元素失配，模式串指针回到第3个元素重配，子串"aabcaa"最长公共前后缀为2

next[8]=3：第8个元素失配，模式串指针回到第3个元素重配，子串"aabcaaa"最长公共前后缀为2

可以看到，next[i]的值总是比它的子串的最长公共前后缀+1，印证了上面的理解

光说不练假把式，上面只是我们人眼推算出来的，代码应该如何实现

void kmp_next(Substr *substr, int *next)
{if(substr == NULL || next == NULL){return;}int i = 1;int j = 0;next[1] = 0;while(i < substr->len){if(j == 0 || substr->str[i] == substr->str[j]){i++;j++;next[i] = j;}else{j = next[j];}}
}

i 指向当前处理的元素，j 指针表示长度为 i 的子串的最长前后缀+1

分析代码：

代码的处理就是上面理解的具象化，所求的值就是：i+1 位置前的长度为 i 的子串的最长公共前后缀+1

代码中可以看到，先让i++，再将j++的值赋给next[i]，求得：next[i+1] = j + 1

一个一个来看：

序号/下标	1	2	3	4	5	6	7	8
模式串	a	a	b	c	a	a	a	a
next[i]	0	1	2	1	1	2	3	3

next[1]：特殊情况，next[1]固定为0；表示模式串第一个元素就和主串的i位置元素失配

next[2]：特殊情况，next[2]固定为1；分析：进入循环后判断：发现 j 为0，则子串"a"最长公共前后缀为0，i 和 j 同时++，next[2] = j = 1；

next[3]：i = 2；j = 1，发现str[1] == str[2]，即子串"aa"最长公共前后缀为1，next[3] = j++ = 2；

next[4]：i = 3；j = 2；发现str[2] != str[3]，即a != b，aa != ab，进入else分支，j = next[2]=1，再次循环判断，发现str[1] != str[3]，即a != b，再次进入else分支，j = next[1] = 0；到这说明"aab"的最长公共前后缀为0；next[4] = j++ = 1；至于这个回退规则，相信花点时间能理解，我就不画蛇添足了；

next[5]：i = 4；j = 1；说明"aab"最长公共前后缀为0，现在要求"aabc"的最长公共前后缀，str[1] != str[4]，进入else分支，j = next[1] = 0；到这说明"aabc"的最长公共前后缀为0；next[5] = j++ = 1；

next[6]：i = 5；j = 1；说明"aabc"最长公共前后缀为0，现在要求"aabca"的最长公共前后缀，str[1] == str[5]，进入if分支，即next[6] = 2；

next[7]：i = 6；j = 2；说明"aabca"最长公共前后缀为1，现在要求"aabcaa"的最长公共前后缀，str[2] == str[6]，进入if分支，即next[7] = 3；

next[8]：i = 7；j = 3；说明"aabcaa"最长公共前后缀为2，现在要求"aabcaaa"的最长公共前后缀，str[3] != str[7]，进入else分支，j = next[3] = 2；str[2] == str[7]；进入if分支，即next[8] = j++ = 3