当前位置： 首页 > news >正文

《算法导论》第 6 章 - 堆排序

news 2025/8/8 12:57:44

引言

        堆排序（Heapsort）是一种高效的排序算法，它利用堆这种数据结构的特性来实现排序。堆排序具有原地排序的特点，且时间复杂度为O(n log n)，这使得它在实际应用中非常受欢迎。此外，堆结构还被广泛应用于实现优先队列，这是一种在许多算法（如 Dijkstra 最短路径算法、Prim 最小生成树算法）中不可或缺的数据结构。

        本章将详细讲解堆的定义、堆的维护、建堆过程、堆排序算法以及优先队列的实现，并提供完整的 C++ 代码示例，帮助大家深入理解并动手实践。

思维导图

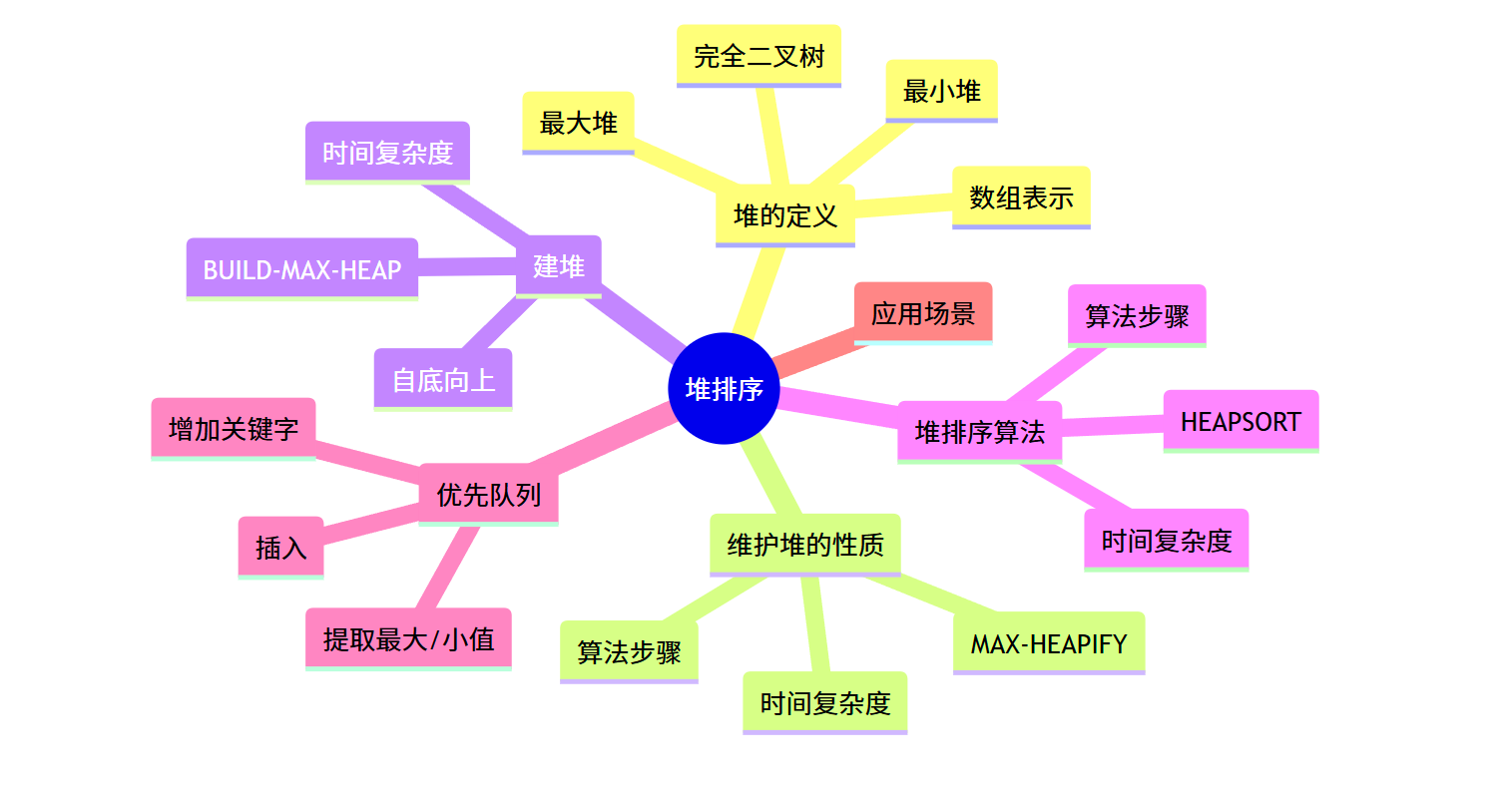
6.1 堆

堆的定义

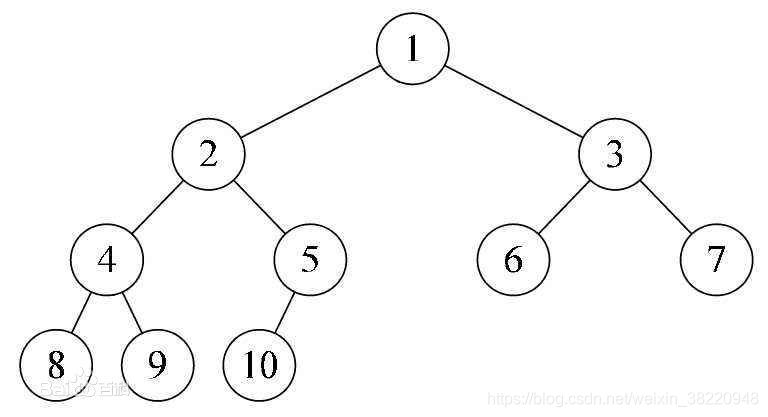
堆（Heap）是一种完全二叉树结构，它具有以下特性：

  • 结构性：堆是一棵完全二叉树，即除了最后一层外，每一层都是满的，且最后一层的节点都靠左排列。
  • 堆序性：对于最大堆，每个节点的值都大于或等于其左右子节点的值；对于最小堆，每个节点的值都小于或等于其左右子节点的值。

        在实际实现中，堆通常用数组来表示，这是因为完全二叉树的结构可以很方便地用数组索引来表示节点之间的关系。

堆的数组表示

对于一个以数组A表示的堆：

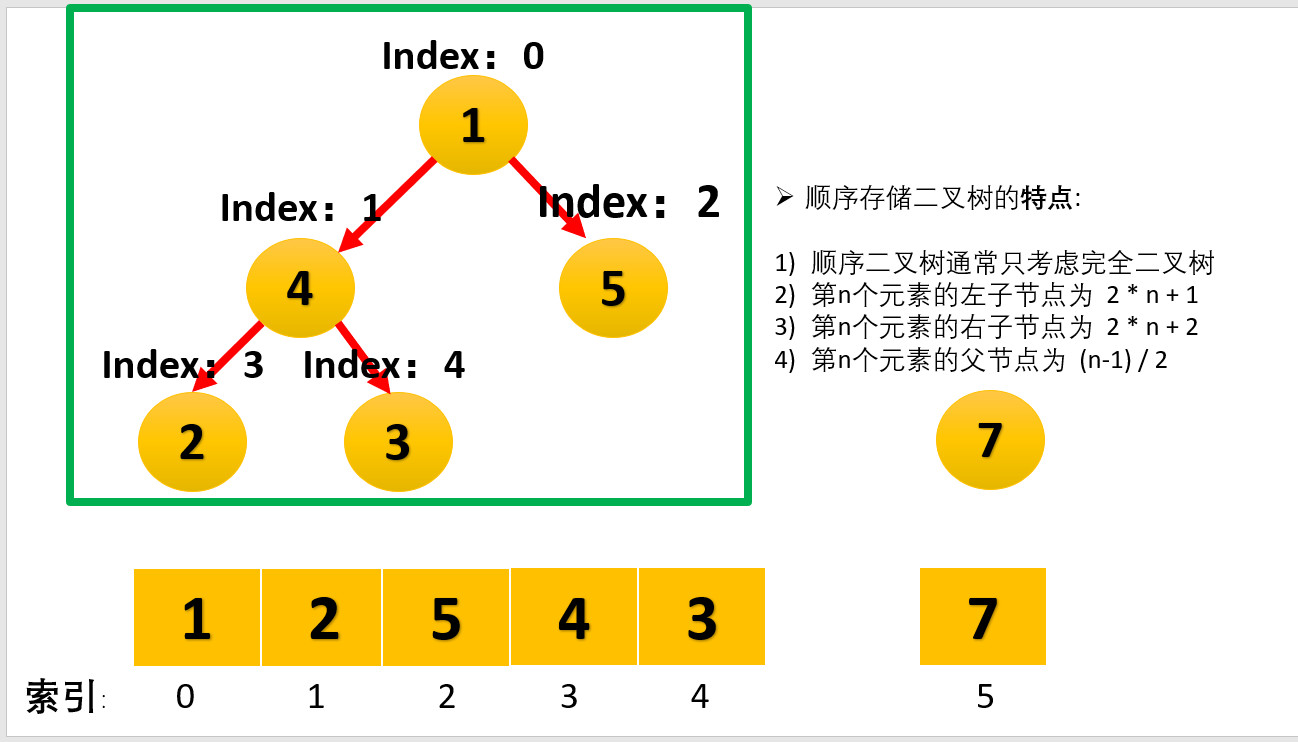
  • 根节点为A[0]（注：《算法导论》中通常以 1 为起始索引，本文为符合 C++ 习惯，使用 0-based 索引）
  • 对于节点i：
    • 父节点为(i - 1) / 2
    • 左子节点为2 * i + 1
    • 右子节点为2 * i + 2

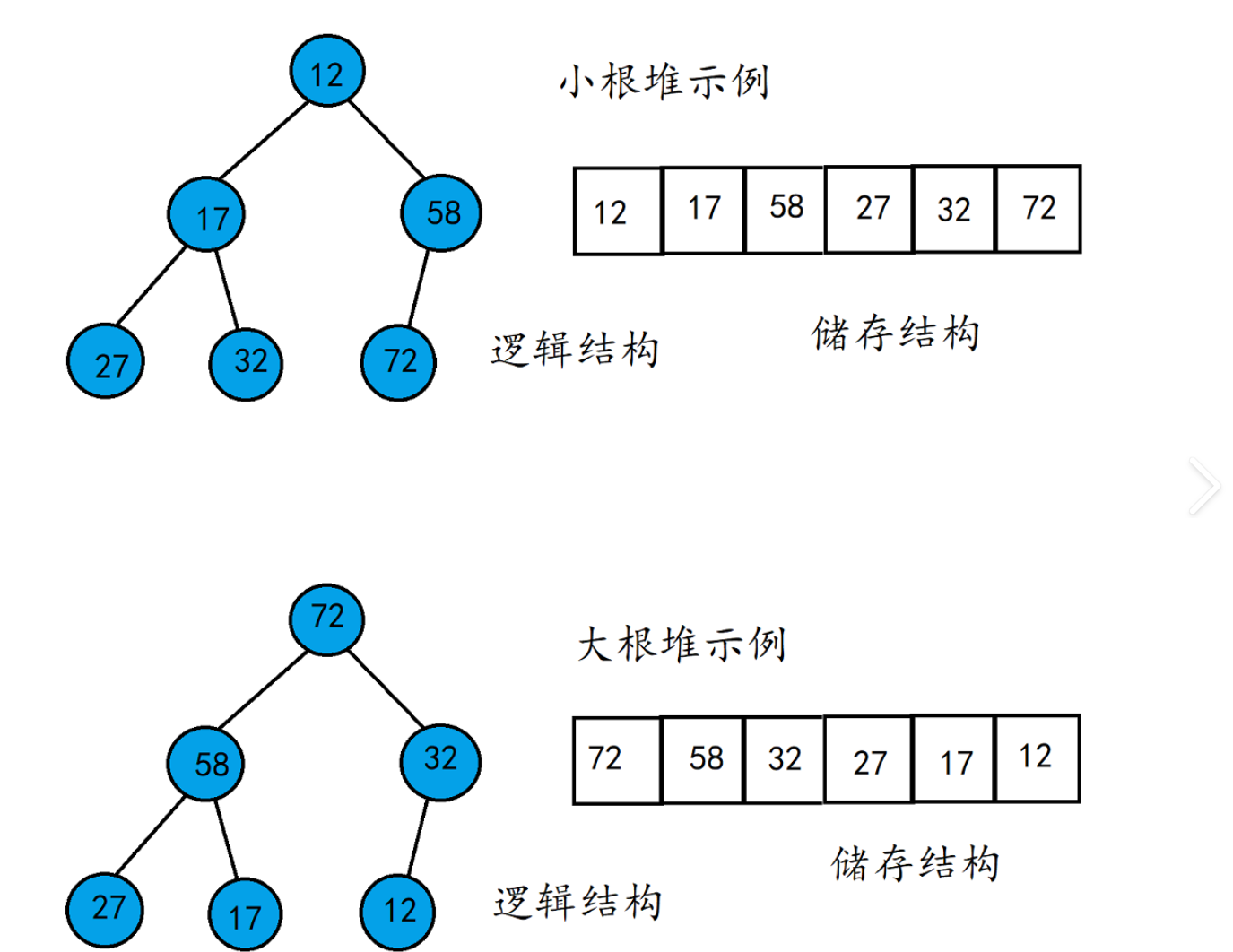
堆的图示

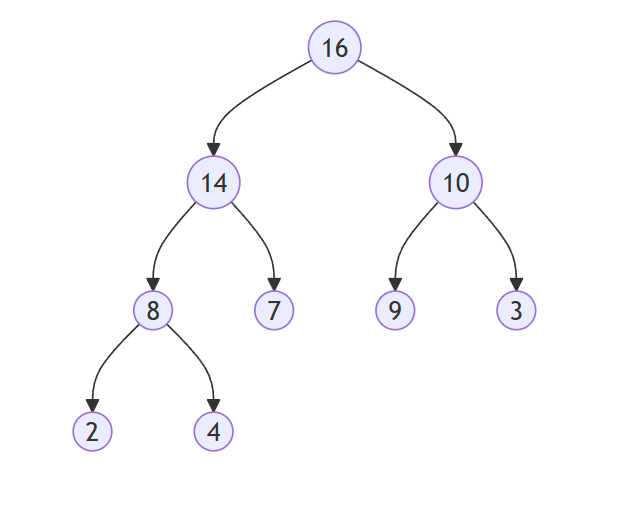
        上图是一个最大堆的示例，对应的数组表示为：[16, 14, 10, 8, 7, 9, 3, 2, 4]

6.2 维护堆的性质

        维护堆的性质是堆操作的核心，对于最大堆而言，这个操作称为MAX-HEAPIFY（最大堆化）。其目的是：当某个节点的值小于其子女的值时，通过交换将该节点 "下沉"，以维护最大堆的性质。

MAX-HEAPIFY 算法步骤

  1. 找到当前节点i、左子节点left、右子节点right中的最大值，记为largest。
  2. 如果largest不是当前节点i，则交换A[i]和A[largest]。
  3. 对largest位置递归执行 MAX-HEAPIFY，直到整棵子树满足最大堆性质。

代码实现

/*** 最大堆化操作* @param A 存储堆的数组* @param n 堆的大小* @param i 需要进行堆化的节点索引*/
void maxHeapify(vector<int>& A, int n, int i) {int largest = i;         // 初始化largest为当前节点int left = 2 * i + 1;    // 左子节点索引int right = 2 * i + 2;   // 右子节点索引// 如果左子节点存在且大于当前节点，更新largestif (left < n && A[left] > A[largest]) {largest = left;}// 如果右子节点存在且大于当前largest，更新largestif (right < n && A[right] > A[largest]) {largest = right;}// 如果largest不是当前节点，需要交换并递归堆化if (largest != i) {swap(A[i], A[largest]);// 递归对交换后的子节点进行堆化maxHeapify(A, n, largest);}
}

示例

        假设我们有一个堆：[16, 4, 10, 14, 7, 9, 3, 2, 8]，其中节点 1（值为 4）违反了最大堆性质。

执行maxHeapify(A, 9, 1)后：

  1. 比较 4、14、7，最大值为 14（右子节点）
  2. 交换 4 和 14，数组变为[16, 14, 10, 4, 7, 9, 3, 2, 8]
  3. 对节点 3（原 14 的位置）继续堆化，比较 4、2、8，最大值为 8
  4. 交换 4 和 8，数组变为[16, 14, 10, 8, 7, 9, 3, 2, 4]
  5. 此时节点 7（原 4 的位置）没有子节点，堆化完成

6.3 建堆

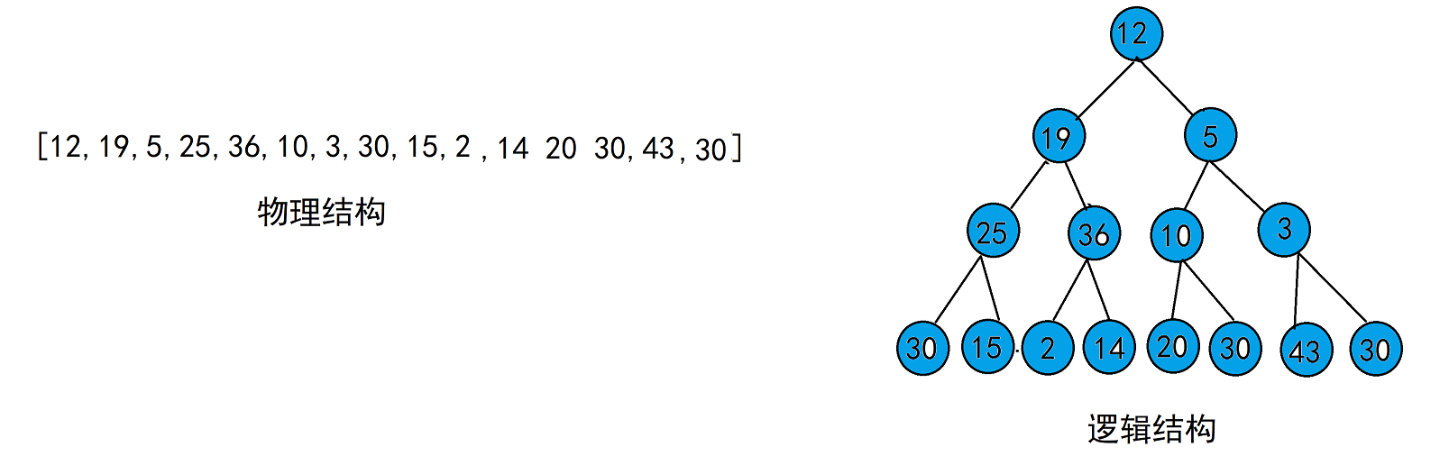
        建堆（BUILD-MAX-HEAP）是将一个无序数组转换为最大堆的过程。其核心思想是：从最后一个非叶子节点开始，自底向上地对每个节点执行 MAX-HEAPIFY 操作。

建堆的原理

  • 完全二叉树中，最后一个非叶子节点的索引为n/2 - 1（0-based）
  • 从该节点开始，向前遍历到根节点，对每个节点执行 MAX-HEAPIFY
  • 这样可以保证每个子树都是最大堆，最终整个树成为最大堆

代码实现

/*** 构建最大堆* @param A 待构建堆的数组* @param n 数组大小*/
void buildMaxHeap(vector<int>& A, int n) {// 从最后一个非叶子节点开始，自底向上进行堆化for (int i = n / 2 - 1; i >= 0; i--) {maxHeapify(A, n, i);}
}

示例

对无序数组[4, 1, 3, 2, 16, 9, 10, 14, 8, 7]建堆：

  1. 最后一个非叶子节点索引为10/2 - 1 = 4（值为 16）
  2. 从 i=4 开始向前遍历：
    • i=4：节点 16 已经是最大堆
    • i=3：节点 2，执行 maxHeapify 后变为 14
    • i=2：节点 3，执行 maxHeapify 后变为 10
    • i=1：节点 1，执行 maxHeapify 后变为 16
    • i=0：节点 4，执行 maxHeapify 后变为 16
  3. 最终得到最大堆：[16, 14, 10, 8, 7, 9, 3, 2, 4, 1]

6.4 堆排序算法

堆排序（Heapsort）利用了最大堆的特性来实现排序，其基本思想是：

  1. 将待排序数组构建成一个最大堆
  2. 不断将堆顶元素（最大值）与堆的最后一个元素交换
  3. 缩小堆的大小，对新的堆顶执行 MAX-HEAPIFY
  4. 重复步骤 2-3，直到整个数组有序

堆排序步骤

  1. 调用 BUILD-MAX-HEAP 将数组构建为最大堆
  2. 从数组末尾开始，循环至第二个元素：
    • 交换堆顶元素（A [0]）和当前堆的最后一个元素（A [i]）
    • 堆的大小减 1（i--）
    • 对新的堆顶执行 MAX-HEAPIFY
  3. 数组已按升序排列

代码实现

/*** 堆排序算法* @param A 待排序的数组* @param n 数组大小*/
void heapSort(vector<int>& A, int n) {// 构建最大堆buildMaxHeap(A, n);// 从最后一个元素开始，逐步将最大值放到正确位置for (int i = n - 1; i > 0; i--) {// 交换堆顶（最大值）和当前堆的最后一个元素swap(A[0], A[i]);// 对剩余的元素执行堆化，注意此时堆的大小为imaxHeapify(A, i, 0);}
}

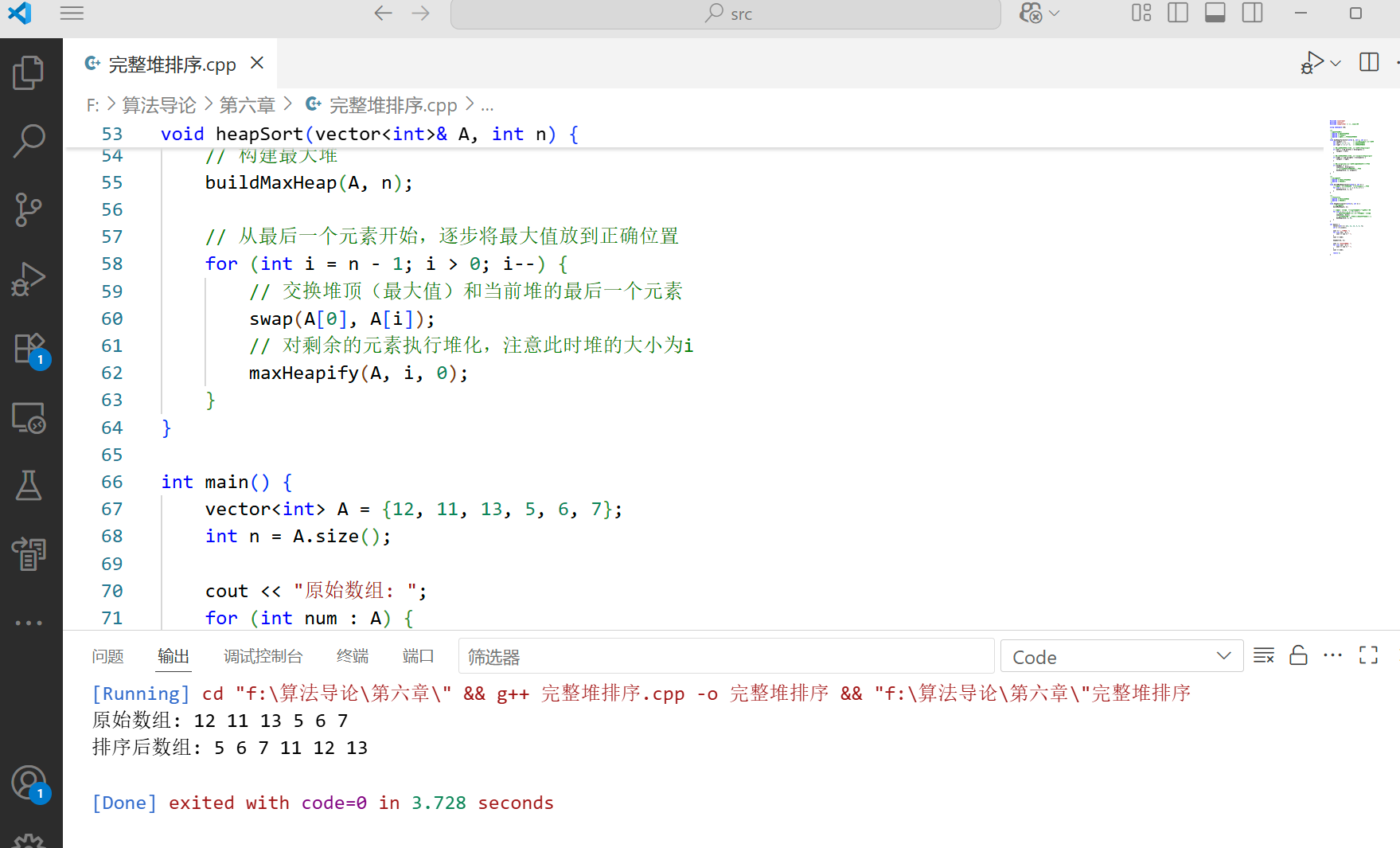
完整堆排序示例

#include <iostream>
#include <vector>
#include <algorithm> // 用于swap函数using namespace std;/*** 最大堆化操作* @param A 存储堆的数组* @param n 堆的大小* @param i 需要进行堆化的节点索引*/
void maxHeapify(vector<int>& A, int n, int i) {int largest = i;         // 初始化largest为当前节点int left = 2 * i + 1;    // 左子节点索引int right = 2 * i + 2;   // 右子节点索引// 如果左子节点存在且大于当前节点，更新largestif (left < n && A[left] > A[largest]) {largest = left;}// 如果右子节点存在且大于当前largest，更新largestif (right < n && A[right] > A[largest]) {largest = right;}// 如果largest不是当前节点，需要交换并递归堆化if (largest != i) {swap(A[i], A[largest]);// 递归对交换后的子节点进行堆化maxHeapify(A, n, largest);}
}/*** 构建最大堆* @param A 待构建堆的数组* @param n 数组大小*/
void buildMaxHeap(vector<int>& A, int n) {// 从最后一个非叶子节点开始，自底向上进行堆化for (int i = n / 2 - 1; i >= 0; i--) {maxHeapify(A, n, i);}
}/*** 堆排序算法* @param A 待排序的数组* @param n 数组大小*/
void heapSort(vector<int>& A, int n) {// 构建最大堆buildMaxHeap(A, n);// 从最后一个元素开始，逐步将最大值放到正确位置for (int i = n - 1; i > 0; i--) {// 交换堆顶（最大值）和当前堆的最后一个元素swap(A[0], A[i]);// 对剩余的元素执行堆化，注意此时堆的大小为imaxHeapify(A, i, 0);}
}int main() {vector<int> A = {12, 11, 13, 5, 6, 7};int n = A.size();cout << "原始数组: ";for (int num : A) {cout << num << " ";}cout << endl;heapSort(A, n);cout << "排序后数组: ";for (int num : A) {cout << num << " ";}cout << endl;return 0;
}

运行结果：

6.5 优先队列

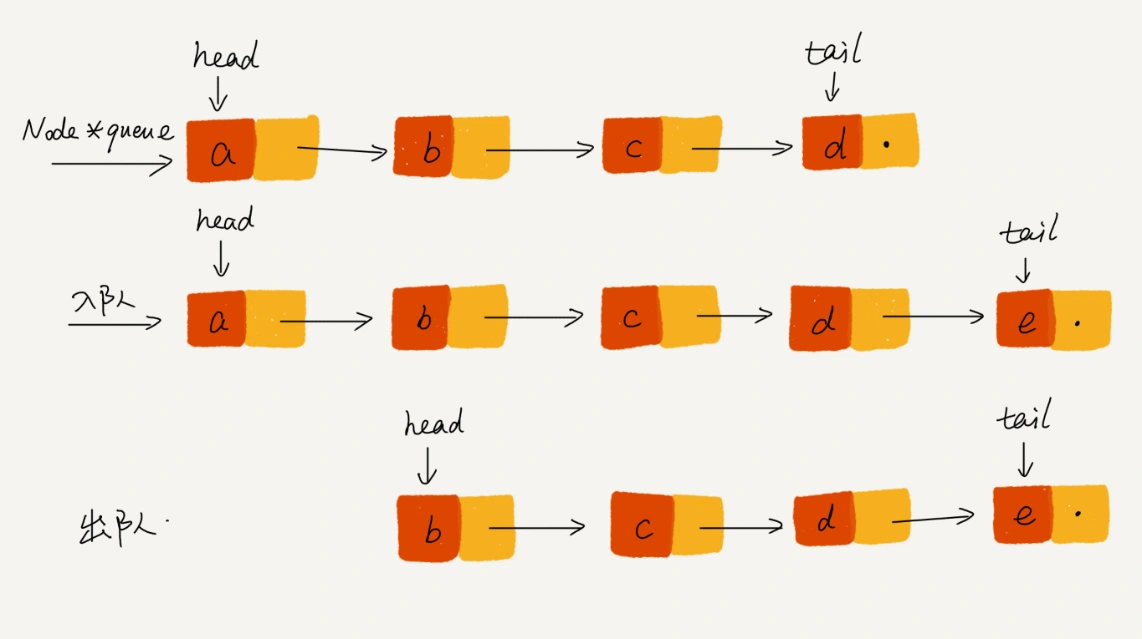
        优先队列（Priority Queue）是一种抽象数据类型，它支持插入元素和提取具有最高优先级元素的操作。堆是实现优先队列的理想数据结构。

优先队列的操作

  • 插入元素（INSERT）：将元素插入到优先队列中
  • 提取最大元素（EXTRACT-MAX）：移除并返回队列中优先级最高的元素
  • 查看最大元素（MAXIMUM）：返回队列中优先级最高的元素，但不移除它
  • 增加关键字（INCREASE-KEY）：增加队列中某个元素的优先级

优先队列的实现

/*** 返回最大堆中的最大值（堆顶元素）* @param A 最大堆数组* @return 最大值*/
int maximum(const vector<int>& A) {return A[0];
}/*** 提取并返回最大堆中的最大值* @param A 最大堆数组* @param n 堆的大小（会被更新）* @return 最大值*/
int extractMax(vector<int>& A, int& n) {if (n < 1) {cerr << "堆下溢" << endl;return -1; // 假设-1不是有效的元素值}int maxVal = A[0];A[0] = A[n - 1]; // 将最后一个元素移到堆顶n--; // 堆大小减1maxHeapify(A, n, 0); // 对新的堆顶执行堆化return maxVal;
}/*** 增加指定元素的关键字值* @param A 最大堆数组* @param i 要增加关键字的元素索引* @param key 新的关键字值（必须大于等于当前值）*/
void increaseKey(vector<int>& A, int i, int key) {if (key < A[i]) {cerr << "新关键字小于当前关键字" << endl;return;}A[i] = key;// 向上调整，确保满足最大堆性质while (i > 0 && A[(i - 1) / 2] < A[i]) {swap(A[i], A[(i - 1) / 2]);i = (i - 1) / 2; // 移动到父节点}
}/*** 向最大堆中插入一个新元素* @param A 最大堆数组* @param n 堆的大小（会被更新）* @param key 新元素的值*/
void insert(vector<int>& A, int& n, int key) {n++; // 堆大小加1A.push_back(INT_MIN); // 在末尾插入一个最小值increaseKey(A, n - 1, key); // 将新插入的元素增加到key值
}

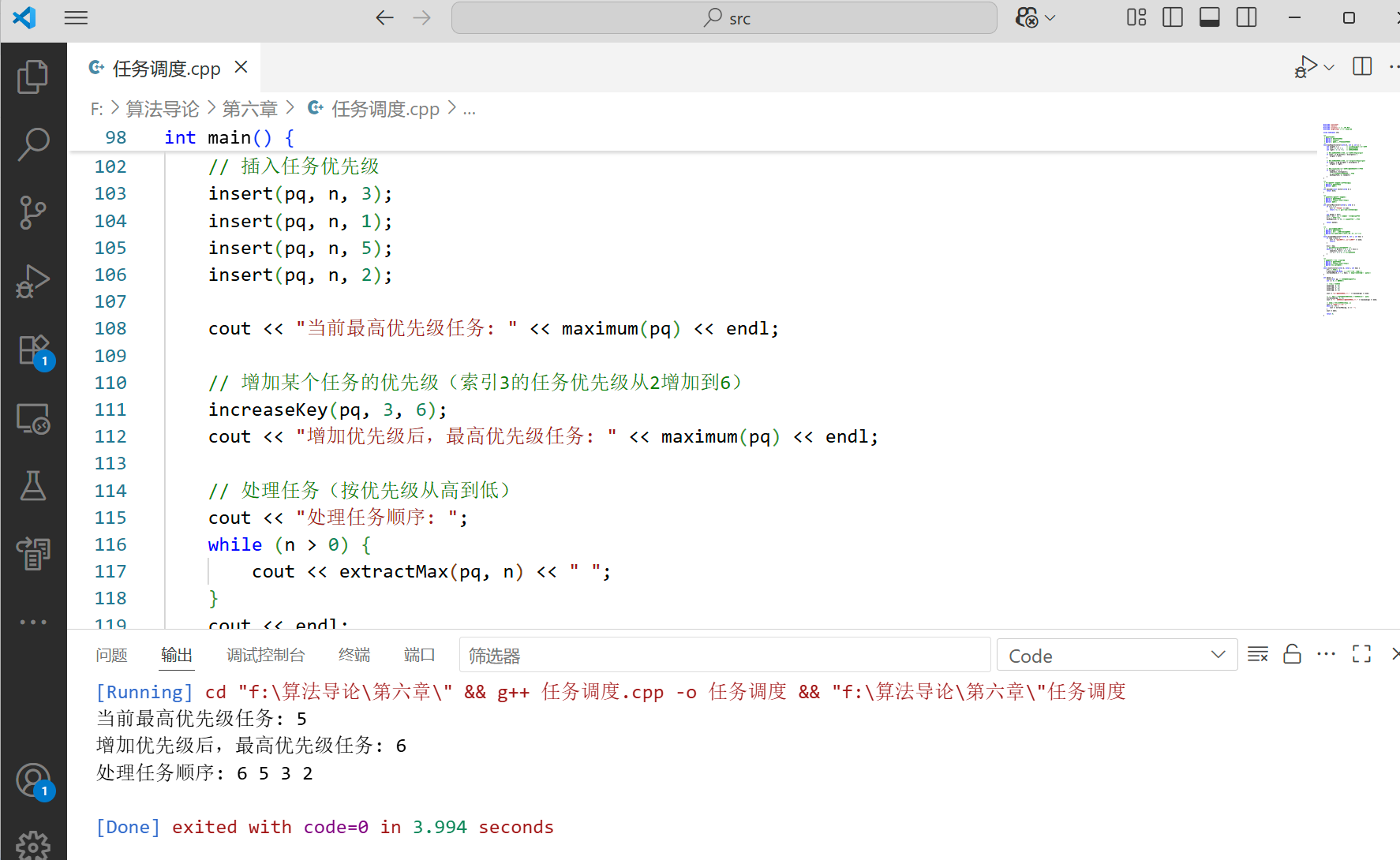
优先队列应用示例：任务调度

#include <iostream>
#include <vector>
#include <climits> // 用于INT_MIN
#include <algorithm> // 用于swap函数using namespace std;/*** 最大堆化操作* @param A 存储堆的数组* @param n 堆的大小* @param i 需要进行堆化的节点索引*/
void maxHeapify(vector<int>& A, int n, int i) {int largest = i;         // 初始化largest为当前节点int left = 2 * i + 1;    // 左子节点索引int right = 2 * i + 2;   // 右子节点索引// 如果左子节点存在且大于当前节点，更新largestif (left < n && A[left] > A[largest]) {largest = left;}// 如果右子节点存在且大于当前largest，更新largestif (right < n && A[right] > A[largest]) {largest = right;}// 如果largest不是当前节点，需要交换并递归堆化if (largest != i) {swap(A[i], A[largest]);// 递归对交换后的子节点进行堆化maxHeapify(A, n, largest);}
}/*** 返回最大堆中的最大值（堆顶元素）* @param A 最大堆数组* @return 最大值*/
int maximum(const vector<int>& A) {return A[0];
}/*** 提取并返回最大堆中的最大值* @param A 最大堆数组* @param n 堆的大小（会被更新）* @return 最大值*/
int extractMax(vector<int>& A, int& n) {if (n < 1) {cerr << "堆下溢" << endl;return -1; // 假设-1不是有效的元素值}int maxVal = A[0];A[0] = A[n - 1]; // 将最后一个元素移到堆顶n--; // 堆大小减1maxHeapify(A, n, 0); // 对新的堆顶执行堆化return maxVal;
}/*** 增加指定元素的关键字值* @param A 最大堆数组* @param i 要增加关键字的元素索引* @param key 新的关键字值（必须大于等于当前值）*/
void increaseKey(vector<int>& A, int i, int key) {if (key < A[i]) {cerr << "新关键字小于当前关键字" << endl;return;}A[i] = key;// 向上调整，确保满足最大堆性质while (i > 0 && A[(i - 1) / 2] < A[i]) {swap(A[i], A[(i - 1) / 2]);i = (i - 1) / 2; // 移动到父节点}
}/*** 向最大堆中插入一个新元素* @param A 最大堆数组* @param n 堆的大小（会被更新）* @param key 新元素的值*/
void insert(vector<int>& A, int& n, int key) {n++; // 堆大小加1A.push_back(INT_MIN); // 在末尾插入一个最小值increaseKey(A, n - 1, key); // 将新插入的元素增加到key值
}int main() {vector<int> pq; // 优先队列（最大堆）int n = 0; // 队列大小// 插入任务优先级insert(pq, n, 3);insert(pq, n, 1);insert(pq, n, 5);insert(pq, n, 2);cout << "当前最高优先级任务: " << maximum(pq) << endl;// 增加某个任务的优先级（索引3的任务优先级从2增加到6）increaseKey(pq, 3, 6);cout << "增加优先级后，最高优先级任务: " << maximum(pq) << endl;// 处理任务（按优先级从高到低）cout << "处理任务顺序: ";while (n > 0) {cout << extractMax(pq, n) << " ";}cout << endl;return 0;
}

运行结果：

思考题

  1. 证明：在一个有 n 个元素的堆中，至多有⌈n/2^(h+1)⌉个高度为 h 的节点。

  2. 说明在最坏情况下，BUILD-MAX-HEAP 的时间复杂度是 O (n)。

  3. 设计一个算法，使用堆来实现选择第 k 小的元素，时间复杂度为 O (n + k log n)。

  4. 如何实现一个最小堆？请修改 MAX-HEAPIFY、BUILD-MAX-HEAP 等函数，实现最小堆及其相关操作。

  5. 设计一个支持合并操作的优先队列（即能将两个优先队列合并为一个），并分析其时间复杂度。

本章注记

  • 堆排序算法是由J. W. J. Williams在 1964 年发明的，同时他也提出了堆这种数据结构。
  • 堆排序的优势在于它是原地排序（只需要 O (1) 的额外空间），且最坏情况下的时间复杂度仍然是 O (n log n)，这一点优于快速排序。
  • 然而，在实际应用中，快速排序通常比堆排序更快，这是因为堆排序的缓存性能较差（访问元素的模式不如快速排序局部化）。
  • 优先队列在许多算法中都有重要应用，如 Dijkstra 最短路径算法、Prim 最小生成树算法、Huffman 编码等。
  • 除了二叉堆，还有其他类型的堆结构，如斐波那契堆（Fibonacci heap）、二项堆（Binomial heap）等，它们在某些操作上具有更好的时间复杂度，但实现更为复杂。

        堆作为一种高效的数据结构，不仅用于排序，还在很多算法和应用中扮演着重要角色。掌握堆的原理和操作，对于提升算法设计能力和解决实际问题都具有重要意义。

        希望本文能帮助你更好地理解堆排序和优先队列，如果有任何疑问或建议，欢迎在评论区留言讨论！

http://www.dtcms.com/a/317803.html

相关文章：

  • MCP-PromptX AI小说创作使用教程
  • Linux（17）——Linux进程信号
  • C++ STL--＞ vector的模拟实现！
  • smart-water表设计方案
  • jdk-24的安装及环境变量配置
  • LazyLLM教程 | 第3讲：大模型怎么玩：用LazyLLM带你理解调用逻辑与Prompt魔法！
  • 【前端开发】四. JS内置函数
  • 芯片封装（DIP、SOP、QFP、QFN、BGA、LGA、PGA）
  • C++音视频流媒体开发面试题：音视频基础
  • OceanBase DBA实战营2期--自动分区分裂学习笔记
  • 机器翻译：语料库的定义与获取，及语料预处理
  • 安宝特方案丨工业AR+AI质检方案：致力于提升检测精度与流程效率
  • 无人机航拍数据集|第6期 无人机垃圾目标检测YOLO数据集772张yolov11/yolov8/yolov5可训练
  • LeetCode 分类刷题：611. 有效三角形的个数
  • 阿里云 Flink
  • 稀土新贵醋酸镥：高纯度材料的科技密码
  • 机器人定位装配的精度革命：迁移科技如何重塑工业生产价值
  • [特殊字符]企业游学 | 探秘字节，解锁AI科技新密码
  • 智慧养老破局：科技如何让“老有所养”变成“老有优养”？
  • 加载量化模型
  • 7.3 I/O方式 (答案见原书 P315)
  • HashMap 与 ConcurrentHashMap 深度解析
  • Java Stream (二)
  • 【模电笔记】—— 直流稳压电源——稳压电路
  • 从“T+1”到“T+0”：基于SQL构建MES到数据仓库的数据采集通道
  • 嵌入式学习---在 Linux 下的 C 语言学习 Day9
  • 时隔六年！OpenAI 首发 GPT-OSS 120B / 20B 开源模型：性能、安全与授权细节全解
  • PDW分选如何展示到界面上
  • MCU控制ADAU1701，用System Workbench for STM32导入工程
  • 力扣137:只出现一次的数字Ⅱ