机器学习之KNN、贝叶斯与决策树算法
本文章所介绍的机器学习算法在演示过程中使用的API都基于sklearn库
一、KNN算法
K-近邻算法(K-Nearest Neighbors,简称KNN),根据K个邻居样本的类别来判断当前样本的类别,即KNN是一种用于分类的算法
1.算法原理
KNN算法主要是计算当前样本与训练集中每一个样本的特征空间距离,然后在距离最近的k个样本中,选择最多数量的类别作为目标样本的类别。
输入:一个待预测样本和一个已知类别的训练集;
处理:在训练集中找到与该样本距离最近的 k 个样本;
输出:将这 k 个邻居中出现频率最高的类别,作为预测结果。
2.KNN常用距离公式
1. 欧式距离(Euclidean Distance)
d(x,y)=∑i=1n(xi−yi)2 d(\mathbf{x}, \mathbf{y}) = \sqrt{\sum_{i=1}^{n} (x_i - y_i)^2} d(x,y)=i=1∑n(xi−yi)2
适用于数值连续特征,衡量两点之间的“直线距离”。
2. 曼哈顿距离(Manhattan Distance)
d(x,y)=∑i=1n∣xi−yi∣ d(\mathbf{x}, \mathbf{y}) = \sum_{i=1}^{n} |x_i - y_i| d(x,y)=i=1∑n∣xi−yi∣
也叫“城市街区距离”,像棋盘格路径,适合稀疏数据或特征值离散的情况。
3. 闵可夫斯基距离(Minkowski Distance)
d(x,y)=(∑i=1n∣xi−yi∣p)1/p d(\mathbf{x}, \mathbf{y}) = \left( \sum_{i=1}^{n} |x_i - y_i|^p \right)^{1/p} d(x,y)=(i=1∑n∣xi−yi∣p)1/p
是欧式与曼哈顿的泛化形式:
- 当 p=1p = 1p=1,为曼哈顿距离;
- 当 p=2p = 2p=2,为欧式距离;
- ppp 越大,对较大维度差异越敏感。
4. 切比雪夫距离(Chebyshev Distance)
d(x,y)=maxi∣xi−yi∣ d(\mathbf{x}, \mathbf{y}) = \max_{i} |x_i - y_i| d(x,y)=imax∣xi−yi∣
度量所有维度中最大差值的距离,适合棋盘类场景(如国际象棋中的国王移动)。
5. 余弦相似度(Cosine Similarity)→ 常转化为“余弦距离”
cos(x,y)=∑i=1nxiyi∑i=1nxi2⋅∑i=1nyi2 \cos(\mathbf{x}, \mathbf{y}) = \frac{\sum_{i=1}^n x_i y_i}{\sqrt{\sum_{i=1}^n x_i^2} \cdot \sqrt{\sum_{i=1}^n y_i^2}} cos(x,y)=∑i=1nxi2⋅∑i=1nyi2∑i=1nxiyi
余弦距离为:
dcosine(x,y)=1−cos(x,y)
d_{\text{cosine}}(\mathbf{x}, \mathbf{y}) = 1 - \cos(\mathbf{x}, \mathbf{y})
dcosine(x,y)=1−cos(x,y)
用于文本或高维稀疏向量之间的角度相似度比较。
3.API
from sklearn.neighbors import KNeighborsClassifier# 创建对象
model = KNeighborsClassifier(n_neighbors=5,mertic='euclidean')
# 训练数据
model.fit(x_train, y_train)
n_neighbors:近邻数,与样本距离最短的样本个数,默认为5。
mertic:计算距离的方法
'euclidean':欧式距离(默认)'manhattan':曼哈顿距离'minkowski':闵可夫斯基距离'chebyshev':切比雪夫距离'cosine':余弦距离
根据不同数据选用不同距离计算方法:
| 数据特点 | 推荐距离 |
|---|---|
| 数值型、连续型特征 | 欧式距离(默认) |
| 特征稀疏或有离散值 | 曼哈顿距离 |
| 对异常值不敏感需求 | 曼哈顿 or 切比雪夫 |
| 文本/高维稀疏向量 | 余弦相似度 |
| 想调节对差异的敏感程度 | 闵可夫斯基(调 p) |
4.缺点
KNN算法因其在预测过程中需要对特征距离进行运算,所以其主要特点是训练快,预测慢。
并且,当数据维度过高,即特征过多,但样本之间某些特征差异不大或者毫无差异,计算其距离量的意义不大。
在关于k值得选取上,还需要花费时间进行调整,因为在实际运用中要保证高的准确率和最快的时间;并且当k取1或者取与测试样本数时,这个算法就变得没有价值。(为1时就取距离最近的值,容易被噪声数据干扰;为测试样本数时则直接取样本中数量最多的那一类作为预测值)
二、朴素贝叶斯算法
1.算法原理
朴素贝叶斯算法也是一种分类算法,他是基于数学概率论中的贝叶斯公式,为避免概率为0的情况,算法通常会引入平滑处理(如拉普拉斯平滑),通过先验概率得到后验概率的一种算法。
该算法会计算出所有类别结果的概率,然后选取最大概率的类别作为预测结果。
朴素贝叶斯定理的数学公式:
P(a∣X)=P(x1∣a)P(x2∣a)...P(xn∣a)P(a)P(X)P(a|X) = \frac{P(x_1|a)P(x_2|a)...P(x_n|a)P(a)}{P(X)}P(a∣X)=P(X)P(x1∣a)P(x2∣a)...P(xn∣a)P(a)
X指的是样本中所有的特征向量,x1,x2…指的是单独特征向量,a表示结果。
拉普拉斯平滑处理:
假设我们想根据天气情况预测是否会出去玩:
| 天气(Weather) | 出去玩(Play) |
|---|---|
| sunny | no |
| sunny | no |
| overcast | yes |
| rain | yes |
| rain | yes |
| rain | no |
| overcast | yes |
| sunny | yes |
如果天气是 rain,是否出去玩?
总样本数 = 8
- 正类(yes):5
- 负类(no):3
所以:
- P(yes)=58=0.625P(no)=38=0.375 P(\text{yes}) = \frac{5}{8} = 0.625\\ P(\text{no}) = \frac{3}{8} = 0.375 P(yes)=85=0.625P(no)=83=0.375
如果某个天气没出现,比如 P(overcast∣no)
P(overcast∣no)=03=0
P(overcast∣no)= \frac{0}{3} = 0
P(overcast∣no)=30=0
会导致整个公式乘积为 0,模型无法正确处理。所以使用拉普拉斯平滑
离散特征“天气”的可能取值数 N=3:sunny、overcast、rain。
公式:
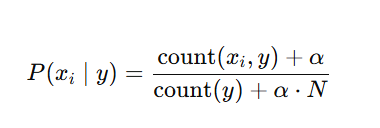
其中α\alphaα=1
计算:

2.API
from sklearn.navie import MultinomialNB()model = MultinomialNB()
model.fit(x_train, y_train)
3.示例
用朴素贝叶斯算法预测红酒种类
from sklearn.datasets import load_wine
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.naive_bayes import MultinomialNB# 获取数据
wine = load_wine()
x, y = wine.data, wine.target
print(wine.feature_names)
# print(x[0])# 数据集分割
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, random_state=12)# 训练
model = MultinomialNB()
model.fit(x_test, y_test)# 评估
y_predict = model.predict(x_test)
print(y_predict)
score = model.score(x_test, y_test)
print(score)# 预测
sample = [[13.05, # Alcohol2.12, # Malic acid2.25, # Ash16.0, # Alcalinity of ash100.0, # Magnesium2.8, # Total phenols3.1, # Flavanoids0.28, # Nonflavanoid phenols2.0, # Proanthocyanins5.0, # Color intensity1.04, # Hue3.0, # OD280/OD3151050.0 # Proline
]]res = model.predict(sample)
print(res)三、决策树
1.概念
决策树是一种分类算法,其结构基于数据结构中的树。下面介绍一些决策树中的概念。
-
决策节点:
将某个特征属性通过条件判断选择分支的节点。 -
叶子节点:
没有子节点的节点,表示最终的决策结果。 -
决策树深度:
节点的最大层次数。 -
优点:可视化,算力要求低。
-
缺点:深度过高会导致过拟合。
可视化的具体表现:
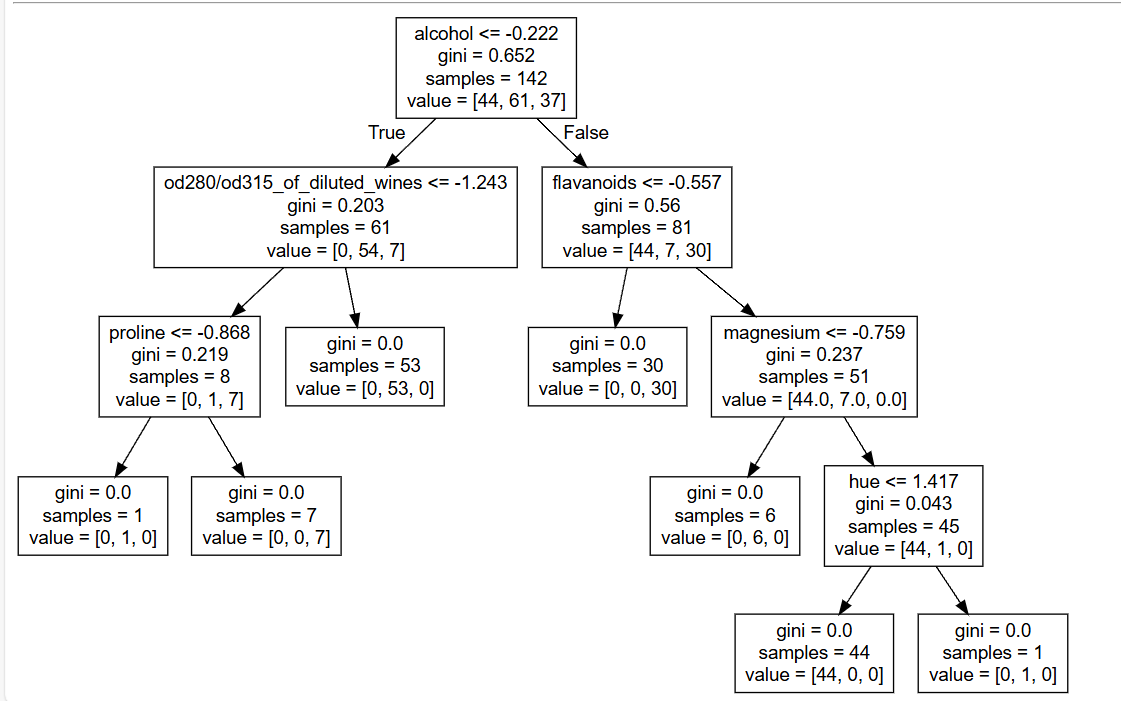
这是sklearn中葡萄酒数据集的决策树分类,最后的叶子节点就是最后所分的种类。即所有叶子节点中的value加起来就是根节点中的value。
那么如何建立决策树呢?选用什么特征作为决策节点呢?我们接下来介绍两种建立决策树的方法。
2.决策树的建立
1.基于信息增益的决策树
在介绍信息增益的概念前我们要先了解什么是信息熵。
信息熵:“熵”表示的是某种事物的混乱程度,那么信息熵就指的是信息的混乱程度——即某个变量的不确定性,熵越大,不确定性越大;熵越小,表示越“纯净”,更容易预测。
信息熵数学公式:
H(X)=−∑i=1npilog2pi
H(X) = -\sum_{i=1}^n p_i \log_2 p_i
H(X)=−i=1∑npilog2pi
-
H(X):表示随机变量 X 的熵
-
pi:表示事件 xi 发生的概率
举个例子:某样本中“是”和“否”的比例为:
- 是(yes):p=0.5p = 0.5p=0.5
- 否(no):p=0.5p = 0.5p=0.5
那么代入公式计算其信息熵$$
H = - (0.5 \log_2 0.5 + 0.5 \log_2 0.5) = - (0.5 \cdot (-1) + 0.5 \cdot (-1)) = 1
结果为1,为二分类(两种类别)中的最大熵值,故表示最大不确定性。
了解完信息熵后,接下来我们介绍信息增益。
信息增益:从原理上来说就是分类前的信息熵与分类后各类的信息熵的加权平均插值的差,即信息不确定性的减少量。
信息增益的数学公式:
Gain(D,A)=H(D)−∑i=1n∣Di∣∣D∣H(Di) \text{Gain}(D, A) = H(D) - \sum_{i=1}^n \frac{|D_i|}{|D|} H(D_i) Gain(D,A)=H(D)−i=1∑n∣D∣∣Di∣H(Di)
因为要将数据进行分类,即要最大程度的减少信息熵,所以在选择决策节点时,需要计算不同属性的信息增益,选择信息增益最大的属性作为决策节点,并且再选择下一决策节点时重复该操作(注意:是重复该操作,而不是基于第一次计算的信息增益去选择,因为在进行一次分类后,信息熵也发生了改变,信息增益也发生了变化)。
举一个简单的案例:
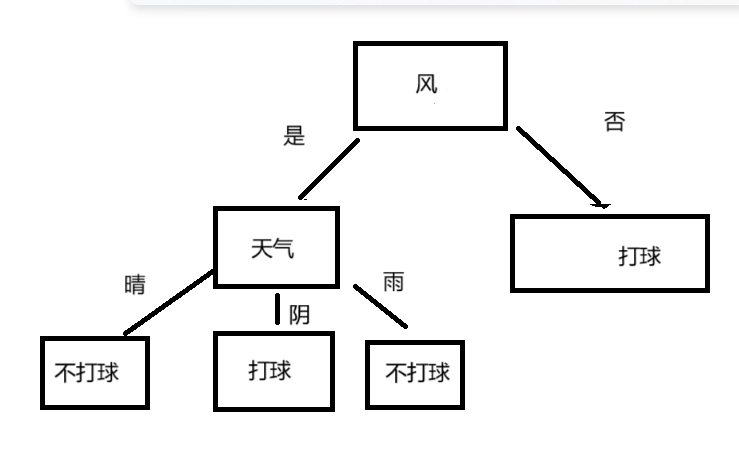
要根据天气是否「晴天」和「是否有风」来预测「是否打球」。
| 编号 | 天气 | 风 | 打球 |
|---|---|---|---|
| 1 | 晴 | 否 | 是 |
| 2 | 晴 | 是 | 否 |
| 3 | 阴 | 否 | 是 |
| 4 | 阴 | 是 | 是 |
| 5 | 雨 | 否 | 是 |
| 6 | 雨 | 是 | 否 |
1、首先,计算出数据集的信息熵:
H(D)=−46log246−26log226≈0.918
H(D) = -\frac{4}{6}\log_2\frac{4}{6} - \frac{2}{6}\log_2\frac{2}{6} ≈ 0.918
H(D)=−64log264−62log262≈0.918
2、用特征”天气“划分的信息增益:
加权平均熵:
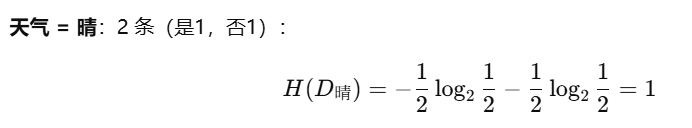
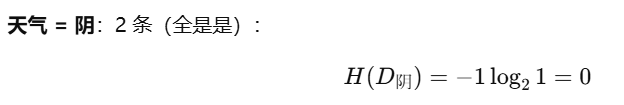
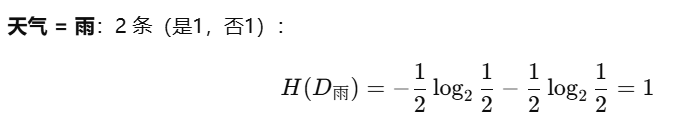
Hweather=26⋅H(D晴)+26⋅H(D阴)+26⋅H(D雨)=26⋅1+26⋅0+26⋅1=46
H_{\text{weather}} = \frac{2}{6} \cdot H(D_{\text{晴}}) + \frac{2}{6} \cdot H(D_{\text{阴}}) + \frac{2}{6} \cdot H(D_{\text{雨}})= \frac{2}{6} \cdot 1 + \frac{2}{6} \cdot 0 + \frac{2}{6} \cdot 1 = \frac{4}{6}
Hweather=62⋅H(D晴)+62⋅H(D阴)+62⋅H(D雨)=62⋅1+62⋅0+62⋅1=64
信息增益 = 0.918 - 0.667 ≈ 0.251
3、用特征“风”作为划分的信息增益:
加权平均熵:
对于 风 = 否,3 个样本全是“是”,所以熵为 0:
H(D风=否)=−1⋅log21=0
H(D_{风=否}) = -1 \cdot \log_2 1 = 0
H(D风=否)=−1⋅log21=0
对于 风 = 是,3 个样本中“是”有 1 个,“否”有 2 个:
H(D风=是)=−13log213−23log223≈0.918
H(D_{风=是}) = -\frac{1}{3}\log_2\frac{1}{3} - \frac{2}{3}\log_2\frac{2}{3} ≈0.918
H(D风=是)=−31log231−32log232≈0.918
Hwind=(3/6)∗0.0+(3/6)∗0.918≈0.459
H_{wind} = (3/6)*0.0 + (3/6)*0.918 ≈ 0.459
Hwind=(3/6)∗0.0+(3/6)∗0.918≈0.459
信息增益 = 0.918 - 0.459 = 0.459
4、比较两个特征的信息增益:
- Gain(D, 天气) = 0.251
- Gain(D, 风) = 0.459
选择“风”作为第一个划分特征,因为它的信息增益更高。
2.基于基尼指数的决策树
基尼指数是一种衡量数据集纯度(纯净度)的指标,用来衡量一个集合中样本的不纯度(即样本类别的混杂程度)。
基尼指数的公式定义为:
Gini(p)=1−∑k=1Kpk2
Gini(p) = 1 - \sum_{k=1}^{K} p_k^2
Gini(p)=1−k=1∑Kpk2
- 当一个节点的所有样本都属于同一类别时,基尼指数为 0,表示纯度最高。
- 当一个节点的样本均匀分布在所有类别时,基尼指数最大,表示纯度最低。
在构建决策树时,我们希望每个内部节点的子节点能更纯,即基尼指数更小。因此,选择分割特征和分割点的目标是使子节点的平均基尼指数最小化。
我们还是用上面那个案例,根据天气是否「晴天」和「是否有风」来预测「是否打球」。
| 编号 | 天气 | 风 | 打球 |
|---|---|---|---|
| 1 | 晴 | 否 | 是 |
| 2 | 晴 | 是 | 否 |
| 3 | 阴 | 否 | 是 |
| 4 | 阴 | 是 | 是 |
| 5 | 雨 | 否 | 是 |
| 6 | 雨 | 是 | 否 |
Gini(D,天气)=26∗(1−(12)2−(12)2)+26∗(1−12)+26∗(1−(12)2−(12)2)
Gini(D,天气) = \frac{2}{6}*(1-(\frac{1}{2})^2-(\frac{1}{2})^2)+\frac{2}{6}*(1-1^2)+\frac{2}{6}*(1-(\frac{1}{2})^2-(\frac{1}{2})^2)
Gini(D,天气)=62∗(1−(21)2−(21)2)+62∗(1−12)+62∗(1−(21)2−(21)2)
Gini(D,天气)=13≈0.333Gini(D,天气) = \frac{1}{3}≈0.333Gini(D,天气)=31≈0.333
Gini(D,风)=12∗(1−(13)2−(23)2)+12∗(1−12)=29
Gini(D,风) = \frac{1}{2}*(1-(\frac{1}{3})^2-(\frac{2}{3})^2)+ \frac{1}{2}*(1-1^2)=\frac{2}{9}
Gini(D,风)=21∗(1−(31)2−(32)2)+21∗(1−12)=92
Gini(D,风)=29≈0.222Gini(D,风) = \frac{2}{9}≈0.222Gini(D,风)=92≈0.222
比较两个属性的基尼指数,可见“风”的基尼指数更小,故选“风”作为第一个决策节点。
3.API
from sklearn.tree import DecisionTreeClassifiertree = DecisionTreeClassifier()
tree.fit(x_train, y_train)
DecisionTreeClassifier()参数:
criterion:“gini”(通过基尼指数构建决策树)、“entropy”(采用信息增益构建决策树),默认为"gini"max_depth:int -->树的最大深度,默认为Nonemin_samples_split:内部节点再划分所需的最小样本数。可以设为绝对数量或比例(如0.1表示10%)。min_samples_leaf:叶子节点所需的最小样本数,也可以设为比例。避免生成样本过少的叶子节点。
可视化决策树
from sklearn.tree import export_graphvizexport_graphviz(estimator, out_file, feature_names)
参数:
estimator:决策树预估器out_file:生成的文档feature_names:节点特征属性名
生成文档文件后,将文档内容复制并粘贴到"http://webgraphviz.com/"中,点击"generate Graph"会生成一个树型的决策树图
4.示例
from sklearn.datasets import load_wine
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.tree import DecisionTreeClassifier, export_graphviz# 获取数据集
wine = load_wine()
x, y = wine.data, wine.target
# 分割
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, random_state=21)
# 预处理
standar = StandardScaler()
x_train = standar.fit_transform(x_train)
x_test = standar.transform(x_test)
# 训练
tree = DecisionTreeClassifier()
tree.fit(x_train, y_train)
# 评估
score = tree.score(x_test, y_test)
y_predict = tree.predict(x_test)
print(y_predict)
print(score)
# 可视化
export_graphviz(tree, out_file="./tree.dot", feature_names=wine.feature_names)以上就是博主在学习机器学习时的一些总结,此文章为个人学习中所作笔记,如有任何错误请及时指正博主,感谢浏览~ovo
