Python-深度学习--2信息熵，条件熵（ID3决策树），KL散度

一、信息熵（Entropy）的计算与应用

信息熵用于衡量一个概率分布的不确定性，值越大表示分布越分散（不确定性越高）。

1. 数学定义

对于离散概率分布 P，信息熵公式为：

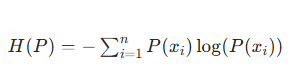
（通常以 2 为底单位是比特，以 e 为底单位是纳特，实际使用中可统一底数）

import numpy as np
from scipy.stats import entropy  # scipy内置熵计算函数def manual_entropy(p):"""手动计算信息熵（确保p是归一化的概率分布）"""# 过滤0概率（避免log(0)无意义）p = p[p > 0]return -np.sum(p * np.log(p))  # 以e为底，若需以2为底可改用np.log2# 示例1：均匀分布（不确定性最高）
p_uniform = np.array([0.25, 0.25, 0.25, 0.25])  # 4个事件等概率
print("均匀分布手动计算熵：", manual_entropy(p_uniform))  # 输出：1.386...（ln4）
print("均匀分布scipy计算熵：", entropy(p_uniform))  # 与手动计算一致# 示例2：极端分布（确定性最高）
p_deterministic = np.array([1.0, 0.0, 0.0, 0.0])  # 只有第一个事件有概率
print("极端分布熵：", entropy(p_deterministic))  # 输出：0.0（无不确定性）# 示例3：实际应用（文本字符分布的熵）
text = "hello world"
char_counts = np.array([text.count(c) for c in set(text)])
char_probs = char_counts / len(text)  # 字符概率分布
print("文本字符分布的熵：", entropy(char_probs))  # 衡量文本字符多样性

运行结果 ：

均匀分布手动计算熵： 1.3862943611198906
均匀分布scipy计算熵： 1.3862943611198906
极端分布熵： 0.0
文本字符分布的熵： 1.5607104090414068

2. Python 实现（手动计算 + 库函数）

import numpy as np
from scipy.stats import entropy  # scipy内置熵计算函数def manual_entropy(p):"""手动计算信息熵（确保p是归一化的概率分布）"""# 过滤0概率（避免log(0)无意义）p = p[p > 0]return -np.sum(p * np.log(p))  # 以e为底，若需以2为底可改用np.log2# 示例1：均匀分布（不确定性最高）
p_uniform = np.array([0.25, 0.25, 0.25, 0.25])  # 4个事件等概率
print("均匀分布手动计算熵：", manual_entropy(p_uniform))  # 输出：1.386...（ln4）
print("均匀分布scipy计算熵：", entropy(p_uniform))  # 与手动计算一致# 示例2：极端分布（确定性最高）
p_deterministic = np.array([1.0, 0.0, 0.0, 0.0])  # 只有第一个事件有概率
print("极端分布熵：", entropy(p_deterministic))  # 输出：0.0（无不确定性）# 示例3：实际应用（文本字符分布的熵）
text = "hello world"
char_counts = np.array([text.count(c) for c in set(text)])
char_probs = char_counts / len(text)  # 字符概率分布
print("文本字符分布的熵：", entropy(char_probs))  # 衡量文本字符多样性

3. 应用场景

• 特征选择：计算特征值的熵，熵越高表示特征越分散，可能包含更多信息。
• 决策树：ID3/C4.5 算法用信息熵计算 “信息增益”，选择最优分裂特征。
• 文本分析：通过字符 / 词频分布的熵衡量文本复杂度（熵越高，字符分布越均匀）。

补充：

步骤 1：计算数据集的总信息熵 H(D)

以经典的 “天气与是否打球” 数据集为例（共 14 条样本）：

编号	天气（A）	温度（B）	湿度（C）	风速（D）	是否打球（标签）
1	晴	hot	高	弱	否
2	晴	hot	高	强	否
3	阴	hot	高	弱	是
...	...	...	...	...	...
14	阴	cool	高	强	是

标签 “是否打球” 中，“是” 有 9 条，“否” 有 5 条，总熵：H(D)=−149​log2​(149​)−145​log2​(145​)≈0.940

步骤 2：对每个特征计算信息增益

以特征 “天气（A）” 为例，其取值为 “晴、阴、雨”：

• 晴（5 条）：2 条 “是”，3 条 “否” → 晴
• 阴（4 条）：4 条 “是”，0 条 “否” → 阴（确定无不确定性）
• 雨（5 条）：3 条 “是”，2 条 “否” → 雨

条件熵：H(D∣A)=145​×0.971+144​×0+145​×0.971≈0.693

信息增益：Gain(D,A)=H(D)−H(D∣A)=0.940−0.693=0.247

同理计算其他特征（温度、湿度、风速）的信息增益，假设结果为：

• 湿度（C）的信息增益最大（约 0.151），则 ID3 选择 “湿度” 作为根节点的分裂特征。

步骤 3：递归构建决策树

对每个特征取值的子集（如 “湿度 = 高”“湿度 = 正常”），重复步骤 1-2，计算子数据集的信息增益，选择下一个分裂特征，直到所有样本属于同一类别或无特征可分。

三、C4.5 算法步骤（改进 ID3 的信息增益比）

C4.5 的核心是用信息增益比替代信息增益，避免 ID3 偏向取值多的特征（如 “日期” 这类取值多的特征可能信息增益高，但无实际意义）。

步骤 1：计算信息增益（同 ID3）

沿用 ID3 中 “天气（A）” 的计算，Gain(D,A)=0.247。

步骤 2：计算特征的熵 HA​(D)

特征 “天气” 有 3 个取值，样本占比分别为 5/14,4/14,5/14：HA​(D)=−145​log2​145​−144​log2​144​−145​log2​145​≈1.577

步骤 3：计算信息增益比

Gain_ratio(D,A)=1.5770.247​≈0.156

对所有特征计算信息增益比，选择增益比最大的特征作为分裂节点（C4.5 通常先筛选信息增益高于平均的特征，再从中选增益比最大的，避免增益接近 0 的特征）。

四、Python 代码实现（ID3 算法示例）

以下用 Python 手动实现 ID3 算法，核心包括信息熵计算、信息增益计算和决策树构建：

import numpy as np
from math import log2   #导入对数函数，用于计算信息熵
import pprint           #导入格式化打印工具，使决策树更易读# 1. 计算信息熵（输入：标签列表，如 ['是', '否', '是', ...]）
def entropy(labels):"""计算标签列表的信息熵"""# 统计每个类别的数量   字典储存 ：键 = 标签， 值 = 出现次数label_counts = {}for label in labels:        #遍历所有标签#如果标签在字典中，次数+1，否则初始化为1label_counts[label] = label_counts.get(label, 0) + 1ent = 0.0                   #初始化信息熵为0total = len(labels)         #总样本数for count in label_counts.values():  #遍历每个类别的数量p = count / total                #计算该类别的概率ent -= p * log2(p)  # 信息熵公式return ent              # 返回计算好的信息熵#作用：衡量数据集的不确定性，值越大表示越混乱
#关键逻辑：用字典统计标签出现次数，带入熵公式计算# 2. 计算信息增益（输入：特征值列表、标签列表）
def information_gain(feature_values, labels):"""计算某一特征的信息增益"""total_ent = entropy(labels)  # 计算总熵total_samples = len(labels)  # 总样本数# 按特征值分组，统计每个取值对应的标签feature_groups = {}  # key: 特征值, value: 该取值对应的标签列表for f_val, label in zip(feature_values, labels):#同时遍历特征值和标签if f_val not in feature_groups:             #如果特征值未记录，初始化列表feature_groups[f_val] = []feature_groups[f_val].append(label)# 计算条件熵 H（D|A）：已知特征A的取值后，数据集的不确定性cond_ent = 0.0for group_labels in feature_groups.values():   # 遍历每个特征值对应的标签列表group_size = len(group_labels)             # 该特征值的样本数# 条件熵 = 求和（该组样本占比 * 该组信息熵）cond_ent += (group_size / total_samples) * entropy(group_labels)return total_ent - cond_ent  # 信息增益 = 总熵 - 条件熵# 3. 选择信息增益最大的特征（输入：特征列表、标签列表）
def choose_best_feature(features, labels):"""选择最佳分裂特征features: 特征列表，格式为 [[f1_val, f1_val, ...], [f2_val, ...], ...]每个子列表对应一个特征的所有取值labels: 标签列表"""best_gain = -1best_feature_idx = 0  # 最佳特征的索引# 遍历每个特征计算信息增益for i in range(len(features)):feature_values = features[i]gain = information_gain(feature_values, labels)if gain > best_gain:  #如果当前增益更大，更新最佳增益和索引。best_gain = gainbest_feature_idx = ireturn best_feature_idx, best_gain  #返回最佳的索引和对应的增益# 4. 递归构建ID3决策树
def build_tree(features, labels, feature_names, depth=0, max_depth=5):"""构建决策树features: 特征列表（格式同上）labels: 标签列表feature_names: 特征名称列表（用于树结构的可读性）"""# 终止条件1：所有标签相同，返回该类别if len(set(labels)) == 1:return labels[0]# 终止条件2：无特征可分或达到最大深度，返回多数类if len(features) == 0 or depth >= max_depth:# 统计多数类label_counts = {}for label in labels:label_counts[label] = label_counts.get(label, 0) + 1return max(label_counts, key=label_counts.get)  # 多数类标签# 选择最佳特征best_idx, _ = choose_best_feature(features, labels)best_feature_name = feature_names[best_idx]best_feature_values = features[best_idx]  # 最佳特征的所有取值# 初始化树结构：以最佳特征为根节点tree = {best_feature_name: {}}# 移除已选择的特征（剩余特征用于子树）remaining_features = [features[i] for i in range(len(features)) if i != best_idx]remaining_feature_names = [feature_names[i] for i in range(len(feature_names)) if i != best_idx]# 按最佳特征的取值分组，递归构建子树unique_values = set(best_feature_values)  # 最佳特征的所有 unique 取值for val in unique_values:# 筛选出该特征值对应的样本索引sample_indices = [i for i, f_val in enumerate(best_feature_values) if f_val == val]# 提取子样本的特征和标签sub_labels = [labels[i] for i in sample_indices]sub_features = []for f in remaining_features:  #遍历剩余特征#提取该特征在子样本中的取值sub_f = [f[i] for i in sample_indices]sub_features.append(sub_f)# 递归构建子树，深度+1 ，并将结果存入当前树结构tree[best_feature_name][val] = build_tree(sub_features, sub_labels, remaining_feature_names, depth + 1, max_depth)return tree# 5. 测试：用天气数据集构建决策树
if __name__ == "__main__":# 构造天气数据集（不依赖pandas，用列表存储）# 特征名称列表feature_names = ['天气', '温度', '湿度', '风速']# 特征值列表：每个子列表对应一个特征的所有取值features = [['晴', '晴', '阴', '雨', '雨', '雨', '阴', '晴', '晴', '雨', '晴', '阴', '阴', '雨'],  # 天气['hot', 'hot', 'hot', 'mild', 'cool', 'cool', 'cool', 'mild', 'cool', 'mild', 'mild', 'mild', 'hot', 'mild'],# 温度['高', '高', '高', '高', '正常', '正常', '正常', '高', '正常', '正常', '正常', '高', '正常', '高'],  # 湿度['弱', '强', '弱', '弱', '弱', '强', '强', '弱', '弱', '弱', '强', '强', '弱', '强']  # 风速]# 标签列表 （是否打球）labels = ['否', '否', '是', '是', '是', '否', '是', '否', '是', '是', '是', '是', '是', '否']  # 是否打球# 构建ID3决策树 （最大深度为3）id3_tree = build_tree(features, labels, feature_names, max_depth=3)# 打印决策树结构 （用pprint格式化输出，更易读）print("ID3决策树结构：")pprint.pprint(id3_tree)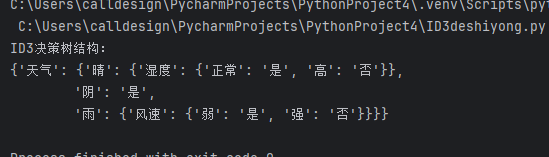

二、KL 散度（Kullback-Leibler Divergence）的计算与应用

KL 散度用于衡量两个概率分布的差异，值越小表示分布越接近（非对称度量）。

1. 数学定义

对于两个离散概率分布 P（真实分布）和 Q（近似分布），KL 散度公式为：

import numpy as np
from scipy.stats import kl_div  # scipy内置KL散度计算def manual_kl_divergence(p, q):"""手动计算KL散度（确保p和q是同维度的归一化概率分布）"""# 过滤0概率（避免log(0)和除以0）p = p[p > 0]q = q[p > 0]  # 只保留p有概率的位置q = np.clip(q, 1e-10, 1.0)  # 防止q为0导致除零错误return np.sum(p * np.log(p / q))# 示例1：两个相似分布的KL散度
p = np.array([0.4, 0.3, 0.3])
q_similar = np.array([0.35, 0.35, 0.3])
print("相似分布手动KL散度：", manual_kl_divergence(p, q_similar))  # 输出：0.014...
print("相似分布scipy KL散度：", np.sum(kl_div(p, q_similar)))  # 与手动计算一致（scipy返回每个元素的KL值，需求和）# 示例2：两个差异大的分布的KL散度
q_different = np.array([0.1, 0.1, 0.8])
print("差异分布KL散度：", np.sum(kl_div(p, q_different)))  # 输出：0.396...（值更大）# 示例3：KL散度的非对称性（P到Q与Q到P的散度不同）
print("D(P||Q)：", np.sum(kl_div(p, q_similar)))
print("D(Q||P)：", np.sum(kl_div(q_similar, p)))  # 结果不同，体现非对称性

3. 应用场景

• 模型评估：衡量预测分布与真实分布的差异（如生成模型中，评估生成数据分布与真实数据分布的差距）。
• 分布对齐：在迁移学习中，用 KL 散度最小化源域与目标域的分布差异。
• 变分自编码器（VAE）：用 KL 散度约束潜在变量分布接近标准正态分布。
• 正则化：在半监督学习中，用 KL 散度限制模型对未标记数据的预测分布熵（如一致性正则化）。