计算机基础速通--数据结构·栈与队列应用

如有问题大概率是我的理解比较片面，欢迎评论区或者私信指正。

强大的意志力的背面是持续的自我对抗，仅仅依靠意志力去学习，我认为这是一件对自己很残忍的事情，因为这样在学习的过程中会面临很多自我对抗，比如该不该玩手机等，最终的结果可能是明明感觉自己很努力了但却没有取得成果，获得消极反馈。以上是我最近学习的感悟，目前我正在尝试一种新的学习方法B=MAP；行为=动机·能力·提示，我理解为：

微笑、微小、适配、方便、习惯和正反馈。

一、基础概念与特性考察

1. 核心定义与操作

栈：强调 “后进先出（LIFO）” 特性，基础操作包括入栈（Push）、出栈（Pop）、取栈顶元素等。

面试可能问：“栈和队列的本质区别是什么？”（答案：栈仅允许在一端操作，队列允许在两端分别进行插入和删除）。

顺序栈和链栈实现

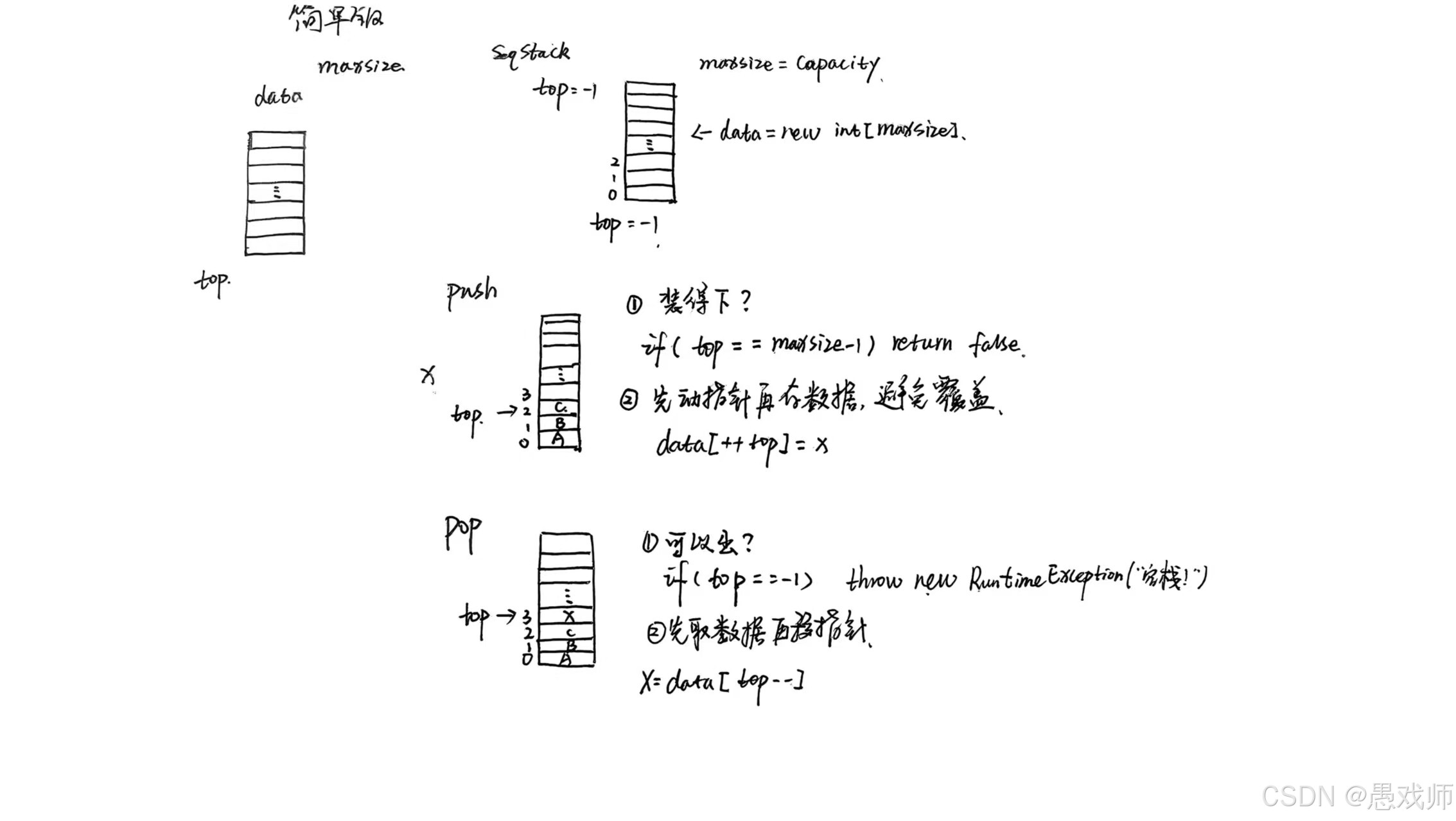
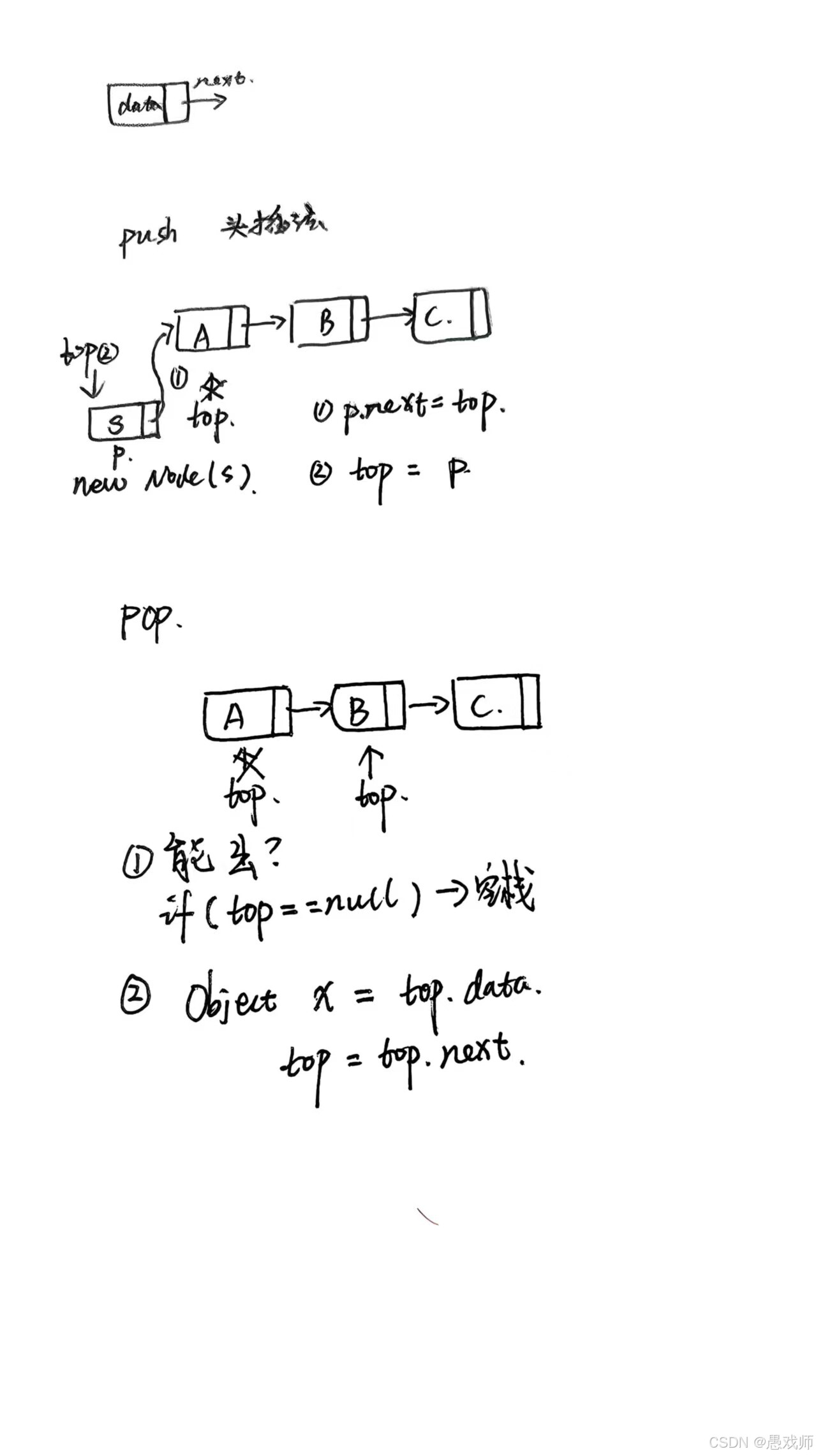
队列：强调 “先进先出（FIFO）” 特性，基础操作包括入队（EnQueue）、出队（DeQueue）、取队头元素等。

延伸考察循环队列的判空 / 判满条件（如牺牲一个空间时，队满条件为(rear+1)%MaxSize == front，队空条件为front == rear）。

在顺序实现中，如何解决假溢出问题，即使用循环队列。循环队列的判空和判满有多种方案：

• 方案一：牺牲一个存储单元（判满条件：(rear+1)%MaxSize == front；判空：front == rear）
• 方案二：增加一个size变量记录队列长度（判空：size==0；判满：size==MaxSize）
• 方案三：增加tag标志（插入操作后tag=1，删除操作后tag=0；判满：front==rear && tag==1；判空：front==rear && tag==0）

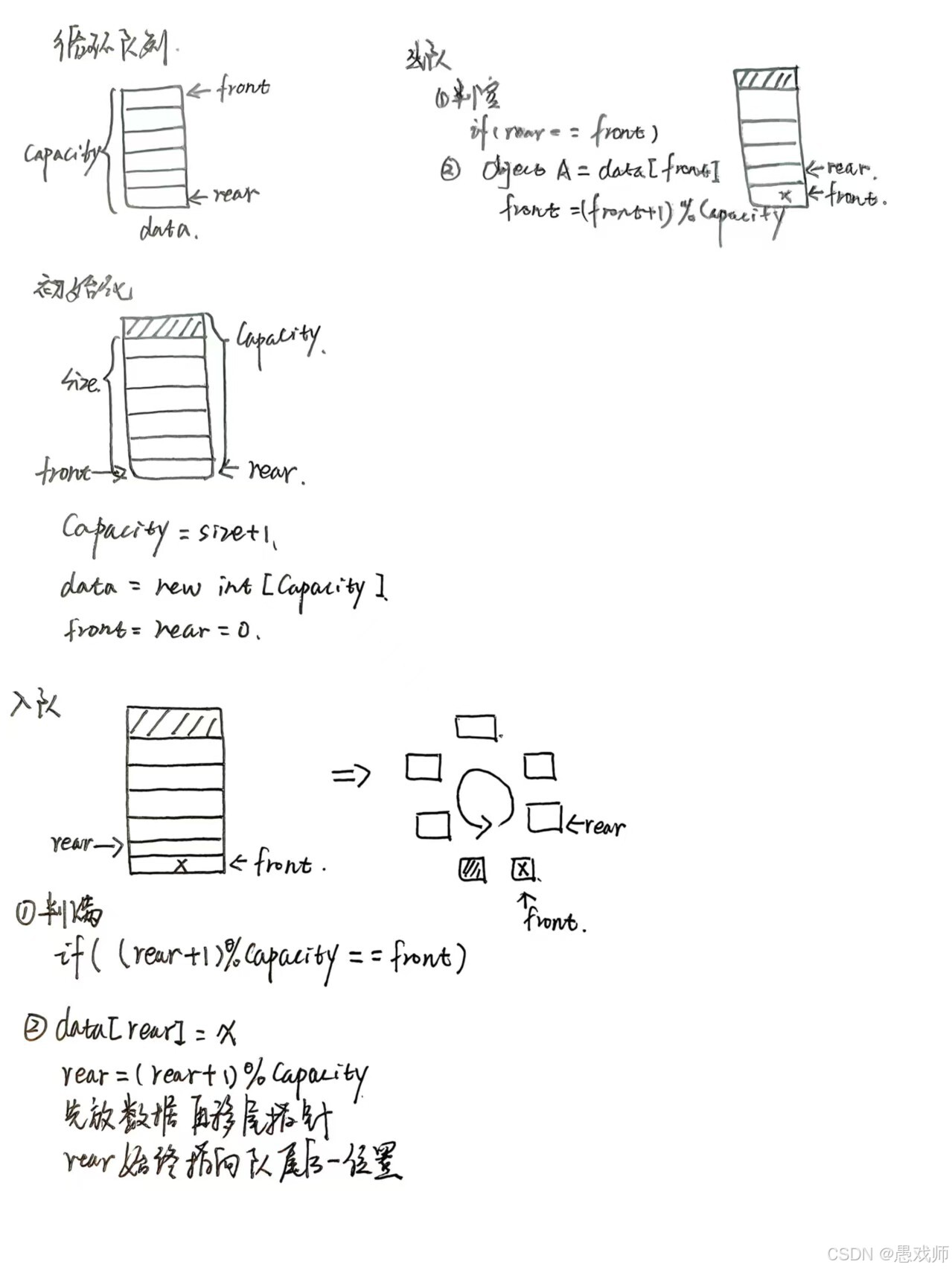
public class ArrayQueue {private final int[] data;private int front; // 队头指针private int rear;  // 队尾指针private final int capacity;// 初始化（牺牲一个存储单元判满）public ArrayQueue(int size) {capacity = size + 1; // 多分配一个空间data = new int[capacity];front = rear = 0;}// 入队操作public boolean enQueue(int x) {if (isFull()) return false;data[rear] = x;rear = (rear + 1) % capacity; // 循环移动return true;}// 出队操作public int deQueue() {if (isEmpty()) throw new RuntimeException("Empty Queue");int val = data[front];front = (front + 1) % capacity; // 循环移动return val;}// 判空：front == rearpublic boolean isEmpty() {return front == rear;}// 判满：(rear+1)%capacity == frontpublic boolean isFull() {return (rear + 1) % capacity == front;}
}

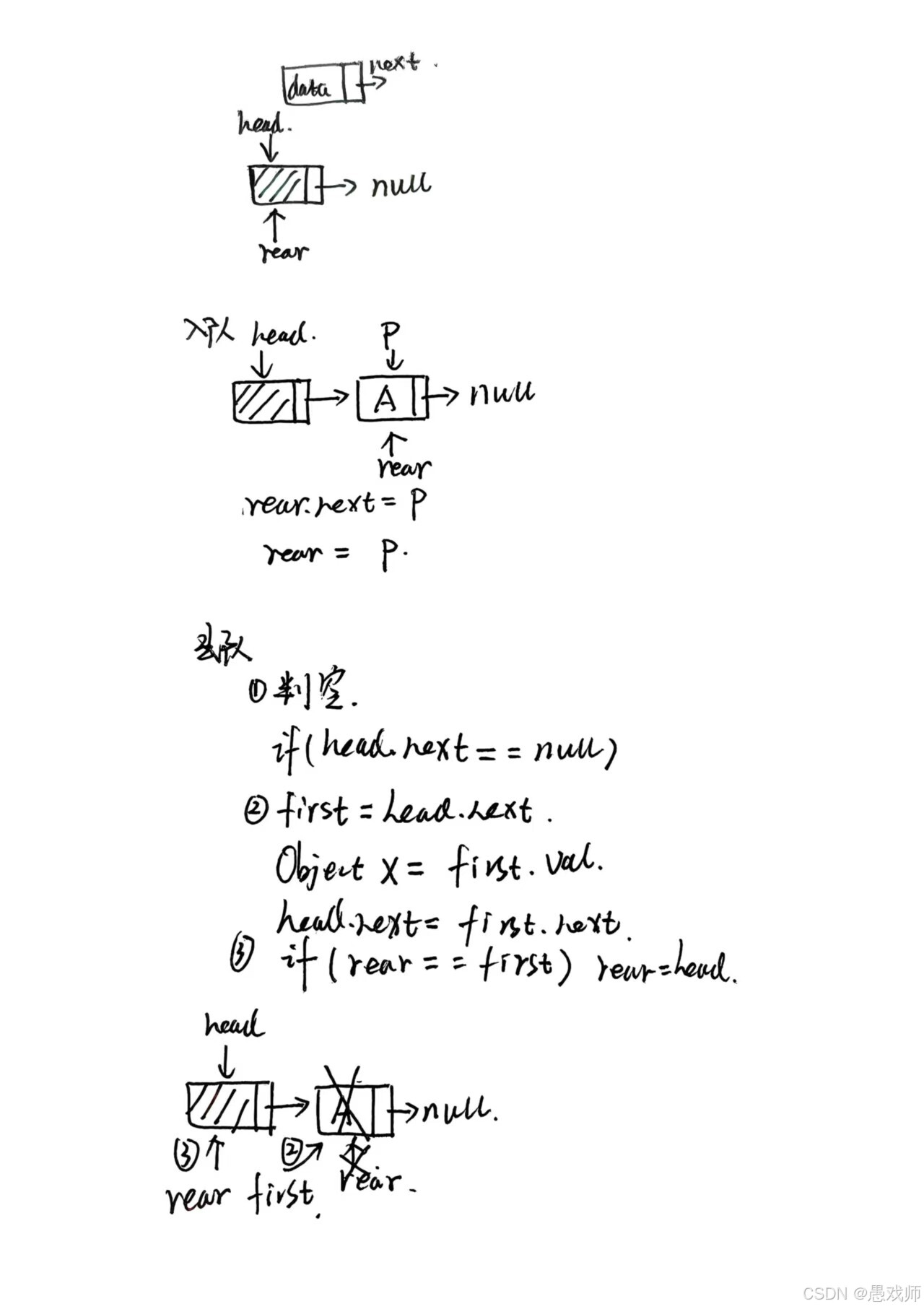
public class LinkedQueue {private static class Node {int val;Node next;Node(int val) { this.val = val; }}private final Node dummyHead = new Node(-1); // 头结点private Node rear = dummyHead;               // 队尾指针// 入队操作public void enQueue(int x) {Node newNode = new Node(x);rear.next = newNode;  // 新节点插入队尾rear = newNode;       // 更新队尾指针}// 出队操作public int deQueue() {if (isEmpty()) throw new RuntimeException("Empty Queue");Node first = dummyHead.next;dummyHead.next = first.next;if (rear == first) rear = dummyHead; // 最后一个节点出队时重置rearreturn first.val;}// 判空：头结点无后继public boolean isEmpty() {return dummyHead.next == null;}
}

数组：连续存储的线性结构，支持随机访问，涉及以下要点：

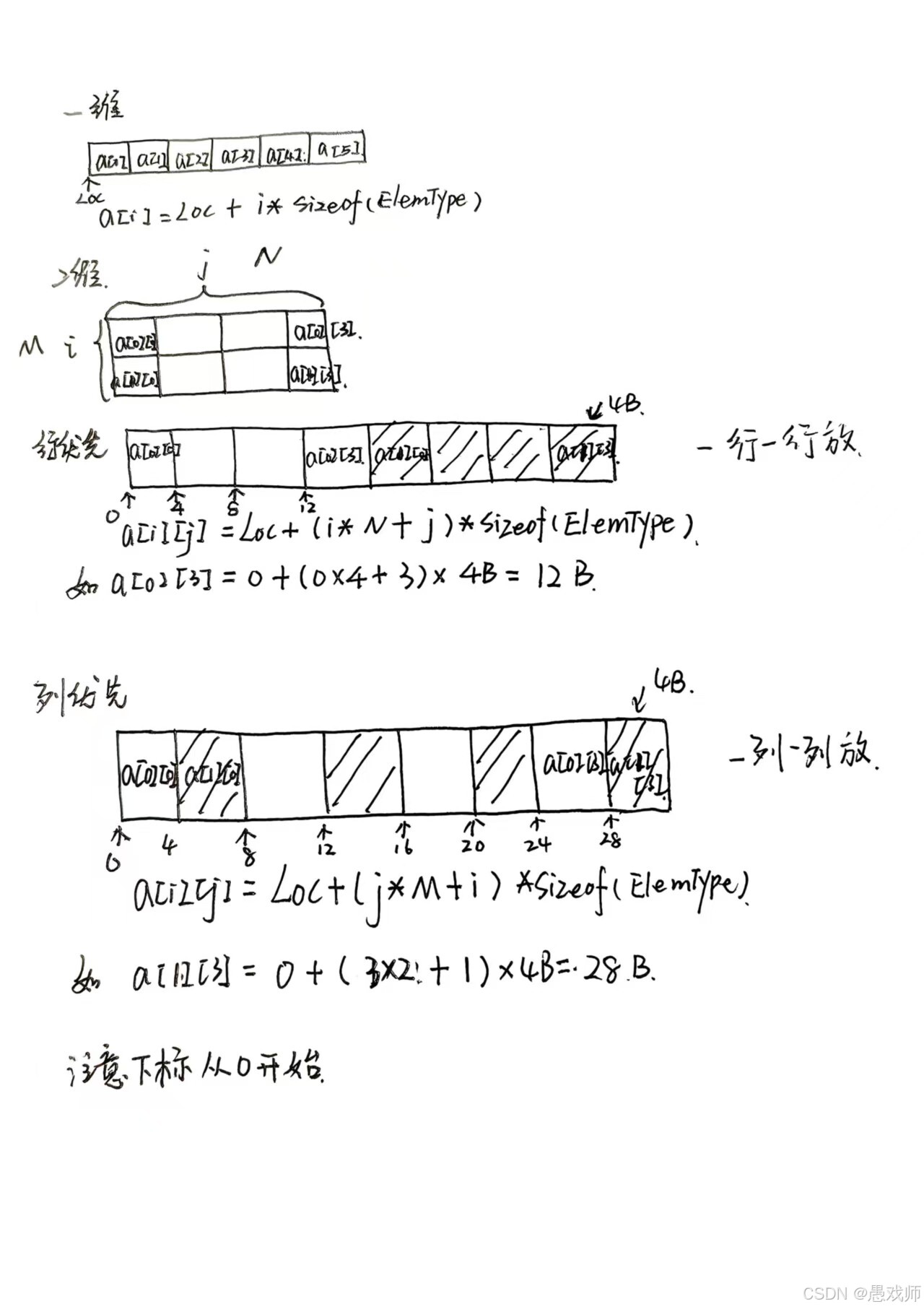
​​基础数组存储​​：一维数组的连续存储地址计算（LOC + i * sizeof(ElemType)）；二维数组的行优先与列优先存储策略及地址公式。

• 行优先存储​​：元素按行顺序连续存放。地址公式：LOC + (i * N + j) * sizeof(ElemType)（M行N列）。

• ​​列优先存储​​：元素按列顺序连续存放。地址公式：LOC + (j * M + i) * sizeof(ElemType)。

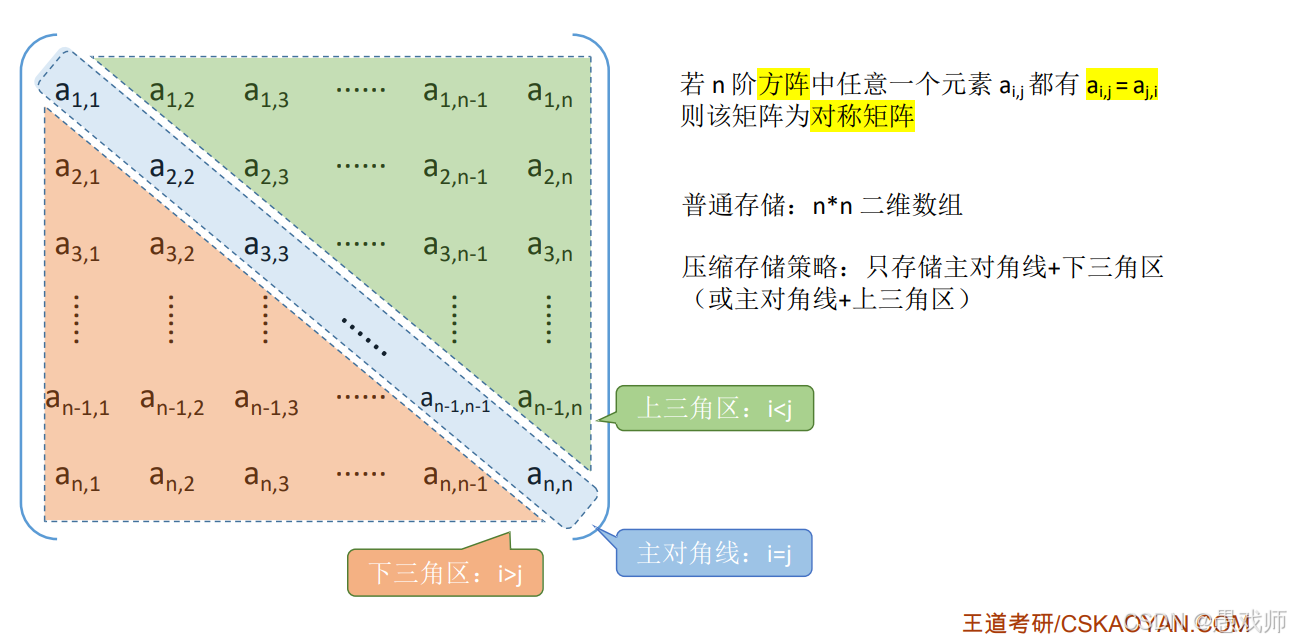
​​特殊矩阵压缩存储​​：针对对称矩阵、三角矩阵（上/下三角）、三对角矩阵（带状矩阵）和稀疏矩阵，通过只存储关键区域（如主对角线+三角区）减少冗余。

压缩存储目的

节省空间：对具有特殊规律（对称性、三角分布、带状分布）或大量零元素（稀疏矩阵）的矩阵，避免存储无效数据。

核心方法：将二维矩阵映射到一维数组，通过数学公式实现下标转换。

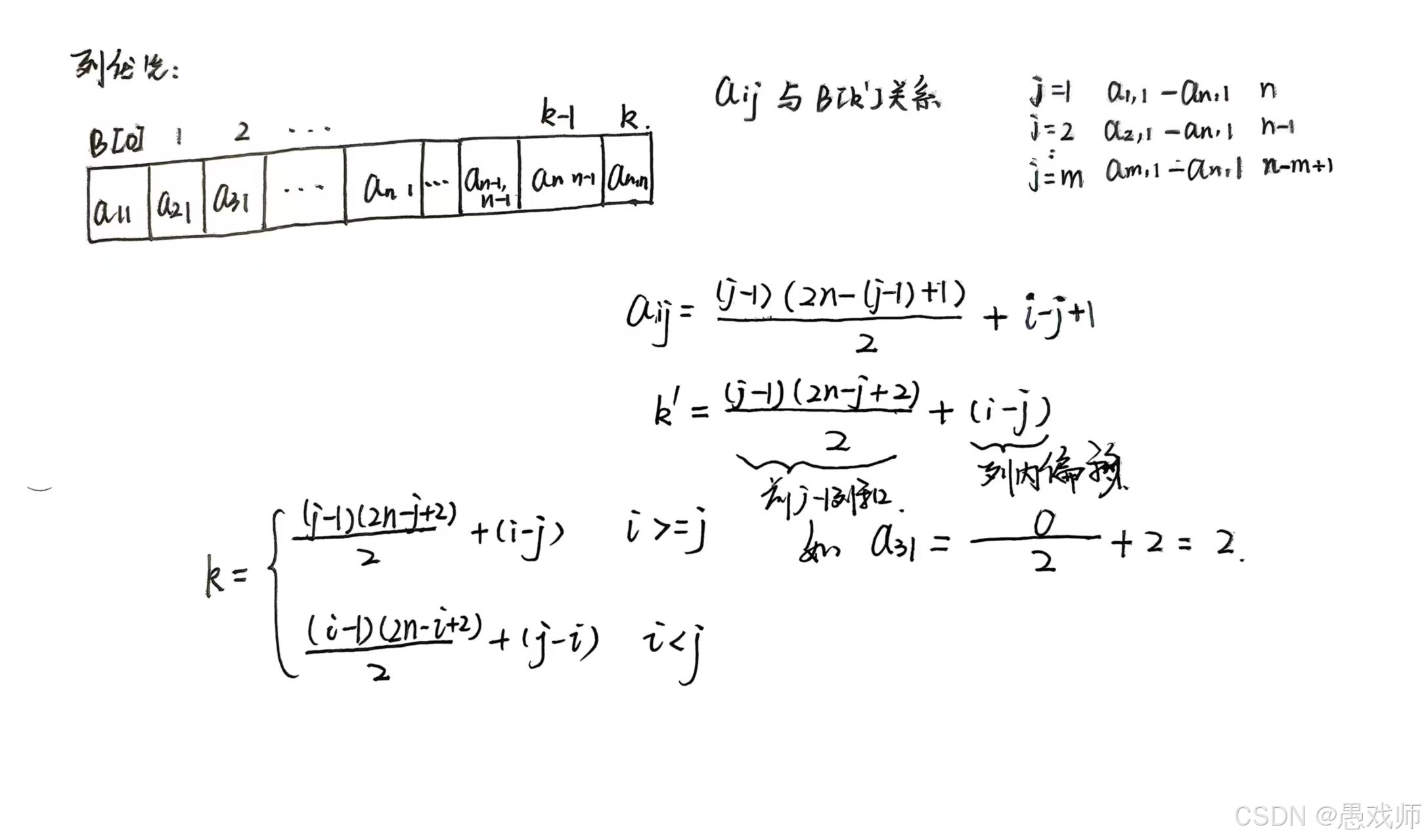
​​存储映射机制​​：为每个压缩策略提供矩阵下标到一维数组索引的映射函数，例如对称矩阵的 k = i(i-1)/2 + j - 1（i ≥ j）。

对称矩阵n*n，关键：

​

三角矩阵的定义​​

三角矩阵分为下三角矩阵和上三角矩阵，其特点是部分区域元素相同，可大幅压缩存储：

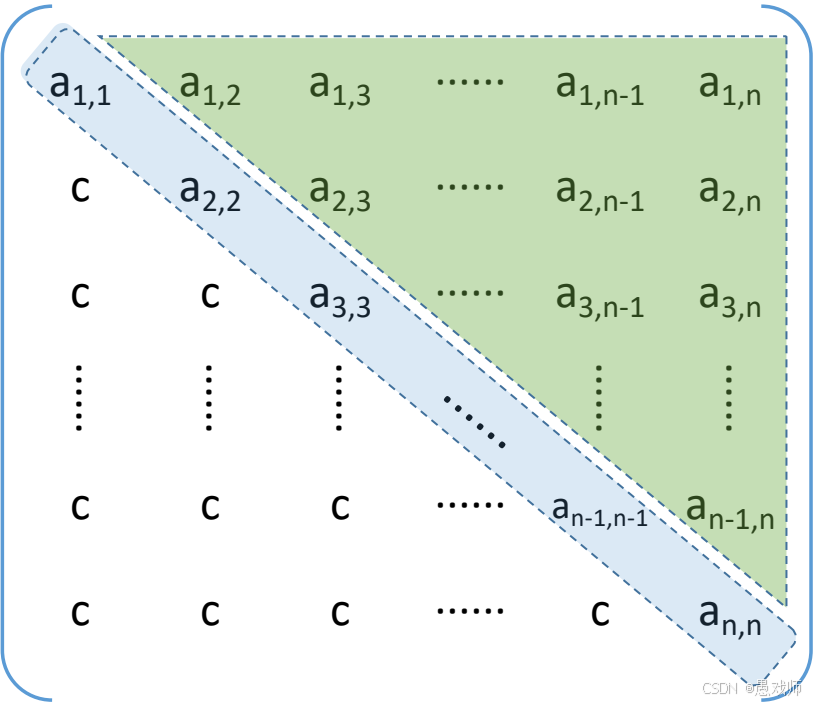
• ​​下三角矩阵​​：除主对角线和下三角区（即 i≥j的位置）外，其余上三角区元素全为相同常量（如常量 c）。

  

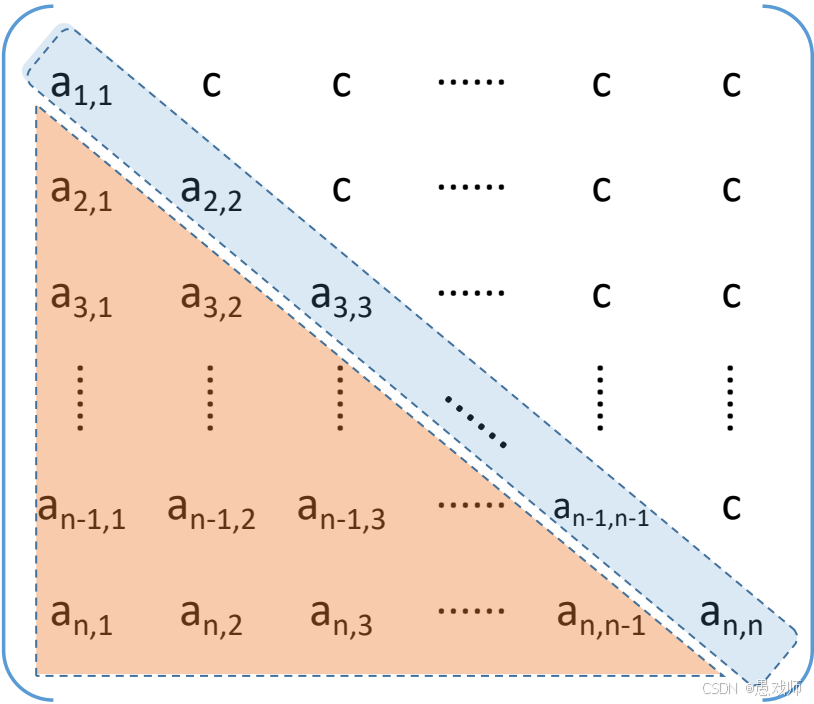
• ​​上三角矩阵​​：除主对角线和上三角区（即 i≤j的位置）外，其余下三角区元素全为相同常量（如常量 c）。

  

​​核心要点​​：

• 矩阵为 n×n方阵。

• 常量区域无需重复存储，仅需存储非常量区域（下三角区或上三角区）和一个常量值。

• ​​存储原则​​：按行优先顺序存入非常量区域元素，末尾追加常量 c。

• ​​下三角矩阵示例​​：

  • 存储元素：主对角线 + 下三角区（其中 i≥j）。

  • 一维数组结构：[a_{1,1}, a_{2,1}, a_{2,2}, a_{3,1}, ..., a_{n,n}, c]。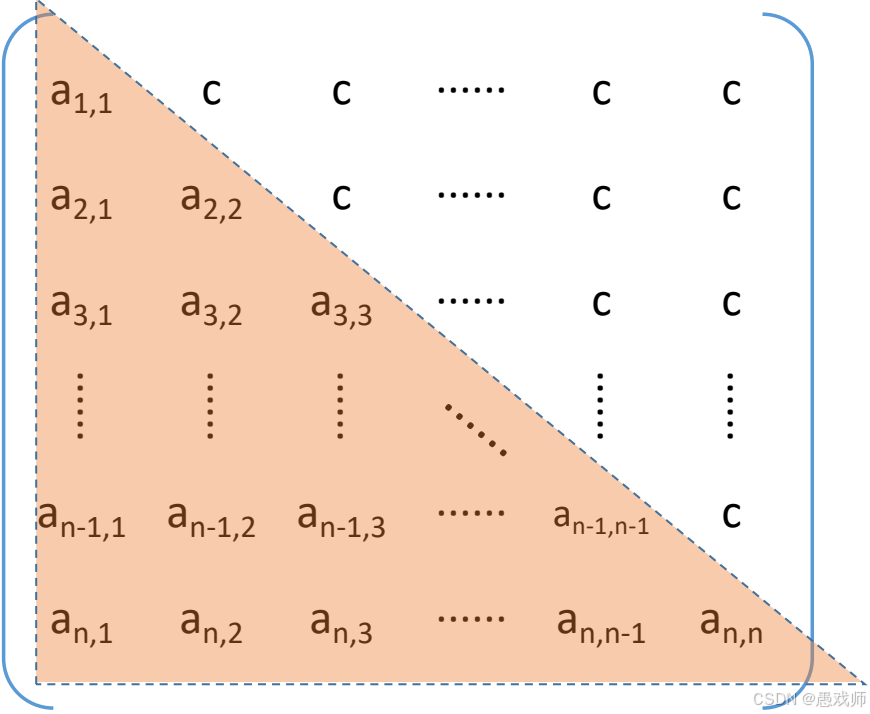

    

• ​​上三角矩阵示例​​：

  • 存储元素：主对角线 + 上三角区（ ai,j​其中 i≤j）。

  • 一维数组结构：[a_{1,1}, a_{1,2}, a_{1,3}, ..., a_{n,n}, c]。

• ​​数组大小​​：非常量元素数 + 1 = 。

下标映射公式​​

矩阵下标 (i,j)到一维数组下标 k的映射是关键操作。公式基于行优先原则：

• ​​下三角矩阵​​：

  • 当 i≥j（下三角区或主对角线）：

    

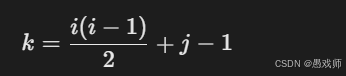
  • 当 i<j（上三角区，元素为常量 c）数组下标从0开始：

    

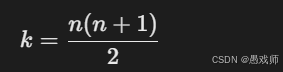
• ​​上三角矩阵​​：

  • 当 i≤j（上三角区或主对角线）：

    

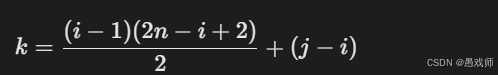
  • 当 i>j（下三角区，元素为常量 c）：

    

稀疏矩阵

核心特点是​​非零元素远少于零元素

核心目标：​​仅存储非零元素​​，忽略零值元素。两种主流策略如下：

​​(1) 顺序存储：三元组法​​

• ​​数据结构​​：每个非零元素表示为三元组 <行, 列, 值>

  • 行/列索引：记录元素位置（默认从1开始，需注意题目要求）

  • 值：元素实际值

• ​​存储结构​​：三元组按行优先顺序存入一维数组

  文档中的三元组表示例：

  i(行)	j(列)	v (值)
  1	3	4
  1	6	5
  ...	...	...

• ​​优点​​：结构简单，空间复杂度仅 O(s)（s为非零元素数）

• ​​缺点​​：插入/删除操作需移动大量元素

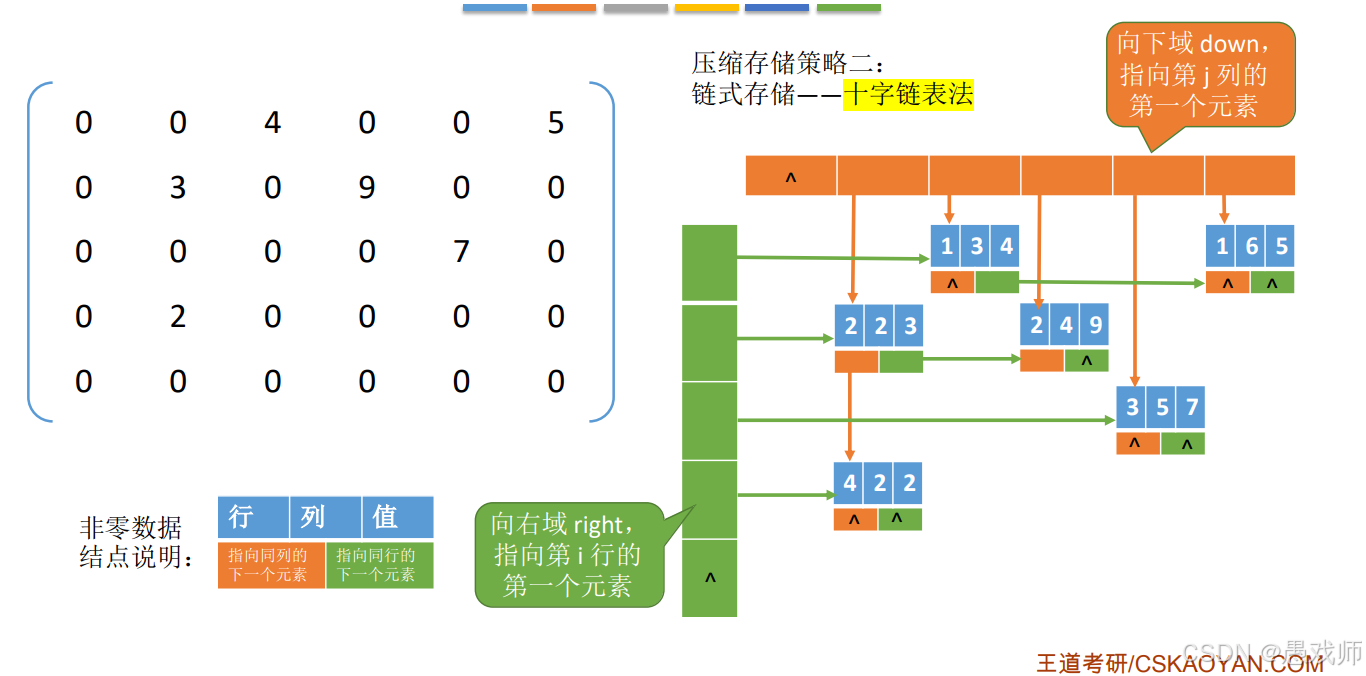
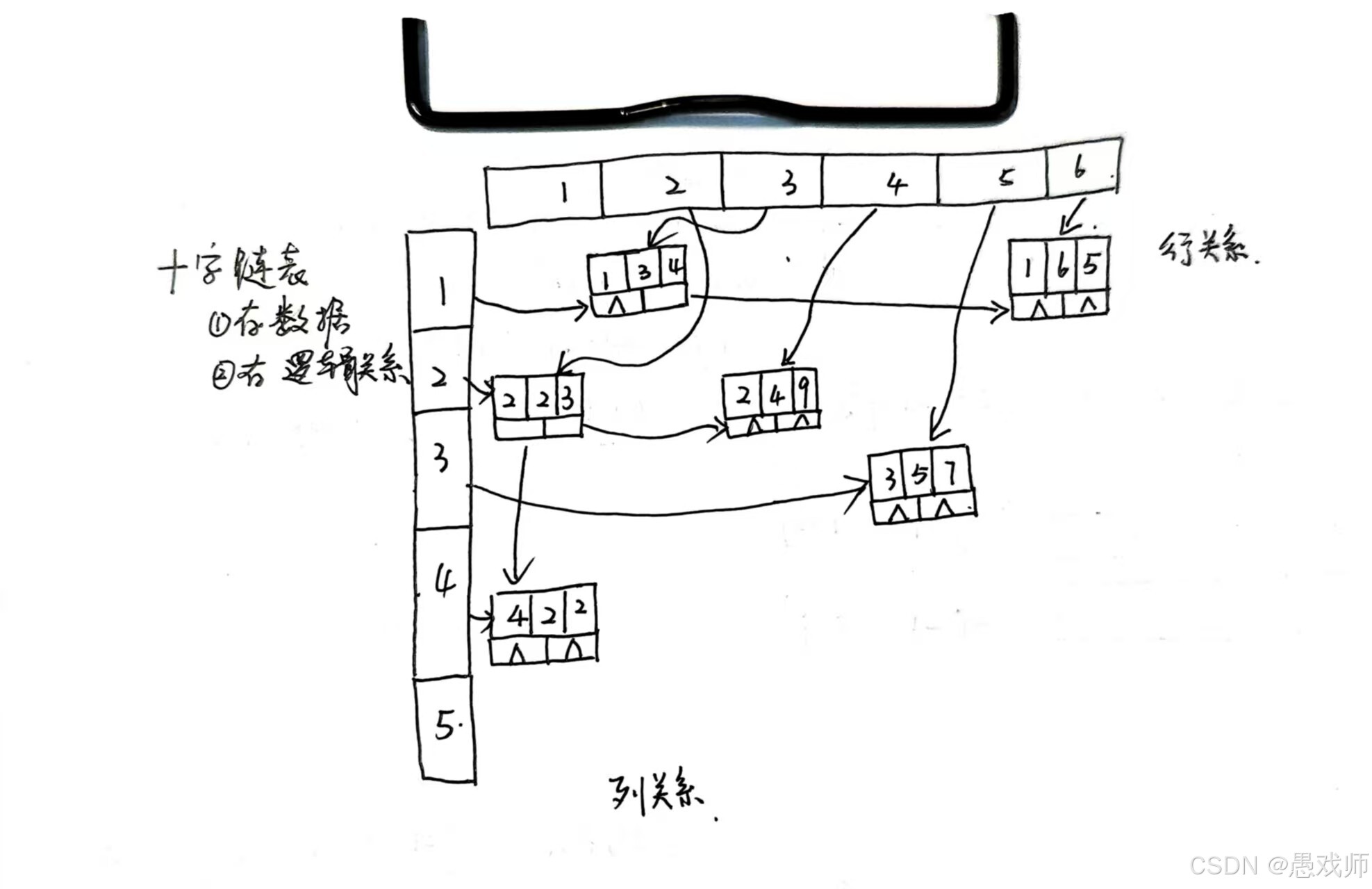
​​(2) 链式存储：十字链表法​​

• ​​数据结构​​：

  • 行指针数组：每行头节点指向该行首个非零元素

  • 列指针数组：每列头节点指向该列首个非零元素

  • 节点结构：<行, 列, 值, 行后继指针, 列后继指针>

• ​​优点​​：高效支持行列遍历，动态插入/删除无需移动元素

• ​​缺点​​：指针占用额外空间

应用场景​​：适用于大规模数据处理，如图像处理（稀疏矩阵）和科学计算（三对角矩阵），能显著降低存储开销。

2. 存储结构对比

栈和队列的顺序存储与链式存储的优缺点：

顺序栈 / 队列可能存在 “假溢出”（循环队列可解决），链式存储无固定容量限制但存在指针开销。

示例问题：“为什么循环队列需要牺牲一个存储空间？”（答案：区分队满和队空状态，避免front == rear时无法判断）。

二、算法设计与实现

1. 栈的经典应用

括号匹配：利用栈检测表达式中括号是否合法（如{[()]}合法，([)]不合法）。

示例：设计算法判断字符串"({})[]"是否有效。20. 有效的括号 - 力扣（LeetCode）

思路：遍历字符串，遇到左括号入栈，遇到右括号则弹出栈顶元素检查是否匹配，最终栈为空则合法。

public boolean isValid(String s) {// 1. 奇偶校验if (s.length() % 2 == 1) return false; // 2. 括号映射表Map<Character, Character> pairs = new HashMap<>() {{put(')', '(');put(']', '[');put('}', '{');}};// 3. 栈处理核心逻辑Deque<Character> stack = new LinkedList<>();for (char ch : s.toCharArray()) {if (pairs.containsKey(ch)) { // 当前是右括号// 3.1 栈空或栈顶不匹配 => 失败if (stack.isEmpty() || stack.peek() != pairs.get(ch)) return false;stack.pop(); // 匹配成功，弹出左括号} else { // 当前是左括号stack.push(ch); // 直接入栈}}return stack.isEmpty(); // 最终栈空校验
}

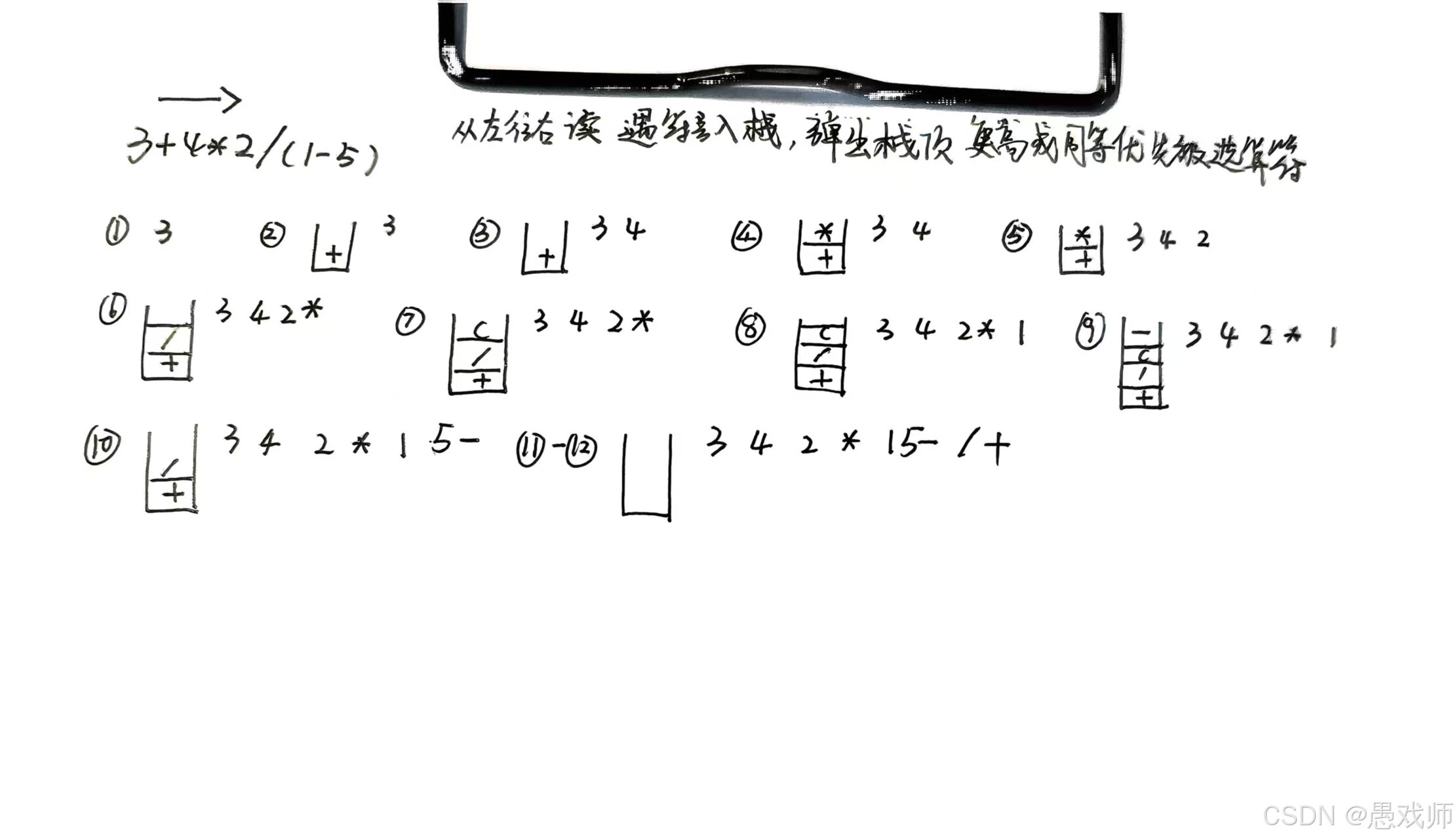
表达式求值：中缀表达式转后缀表达式（利用栈管理运算符优先级），再通过栈计算后缀表达式结果。

示例：将"3+4*2/(1-5)"转为后缀表达式"3 4 2 * 1 5 - / +"，并计算结果。

import java.util.*;public class InfixCalculator {// 运算符优先级映射private static final Map<String, Integer> PRECEDENCE = Map.of("+", 1,"-", 1,"*", 2,"/", 2);// 主计算方法public static double calculate(String infix) {List<String> tokens = tokenize(infix);List<String> postfix = infixToPostfix(tokens);return evalPostfix(postfix);}// 分词处理private static List<String> tokenize(String expression) {List<String> tokens = new ArrayList<>();StringBuilder number = new StringBuilder();for (char c : expression.toCharArray()) {if (Character.isDigit(c) || c == '.') {number.append(c);} else {if (number.length() > 0) {tokens.add(number.toString());number.setLength(0);}if (!Character.isWhitespace(c)) {tokens.add(String.valueOf(c));}}}if (number.length() > 0) {tokens.add(number.toString());}return tokens;}// 中缀转后缀private static List<String> infixToPostfix(List<String> tokens) {List<String> output = new ArrayList<>();Deque<String> stack = new ArrayDeque<>();for (String token : tokens) {if (isNumber(token)) {output.add(token);} else if ("(".equals(token)) {stack.push(token);} else if (")".equals(token)) {while (!stack.isEmpty() && !"(".equals(stack.peek())) {output.add(stack.pop());}if (!stack.isEmpty() && "(".equals(stack.peek())) {stack.pop();}} else if (isOperator(token)) {while (!stack.isEmpty() && !"(".equals(stack.peek()) && PRECEDENCE.getOrDefault(stack.peek(), 0) >= PRECEDENCE.get(token)) {output.add(stack.pop());}stack.push(token);}}while (!stack.isEmpty()) {output.add(stack.pop());}return output;}// 后缀表达式计算private static double evalPostfix(List<String> postfix) {Deque<Double> stack = new ArrayDeque<>();for (String token : postfix) {if (isNumber(token)) {stack.push(Double.parseDouble(token));} else if (isOperator(token)) {double b = stack.pop();double a = stack.pop();switch (token) {case "+": stack.push(a + b); break;case "-": stack.push(a - b); break;case "*": stack.push(a * b); break;case "/": if (b == 0) throw new ArithmeticException("Division by zero");stack.push(a / b); break;}}}return stack.pop();}// 辅助方法private static boolean isNumber(String token) {return token.matches("\\d+(\\.\\d+)?");}private static boolean isOperator(String token) {return PRECEDENCE.containsKey(token);}// 测试方法public static void main(String[] args) {String infix = "3+4 * 2/(1-5)";System.out.println("中缀表达式: " + infix);List<String> tokens = tokenize(infix);System.out.println("分词结果: " + tokens);List<String> postfix = infixToPostfix(tokens);System.out.println("后缀表达式: " + String.join(" ", postfix));double result = calculate(infix);System.out.println("计算结果: " + result);}
}

155. 最小栈 - 力扣（LeetCode）

核心思路：用主栈存数据，用辅助栈存对应的最小值，保持主、辅助栈压入和弹出的同步

class MinStack {Deque <Integer> minStack;Deque <Integer> fuZhuStack;public MinStack() {minStack=new ArrayDeque<Integer>();fuZhuStack=new ArrayDeque<Integer>();minStack.push(Integer.MAX_VALUE);}public void push(int val) {fuZhuStack.push(val);minStack.push(Math.min(minStack.peek(),val));}public void pop() {fuZhuStack.pop();minStack.pop();}public int top() {return fuZhuStack.peek();}public int getMin() {return minStack.peek();}
}

递归模拟：将递归算法转为非递归（如斐波那契数列、二叉树遍历），用栈保存中间状态。

2. 队列的经典应用

层次遍历：二叉树层次遍历需用队列暂存节点，按层输出。（在树和图）

滑动窗口：求数组中滑动窗口的最大值（用双端队列维护窗口内的最大值）。

239. 滑动窗口最大值 - 力扣（LeetCode）https://leetcode.cn/problems/sliding-window-maximum/description/?envType=study-plan-v2&envId=top-100-liked

使用双端队列（Deque）高效地维护滑动窗口内的最大值，核心思想是维护一个单调递减队列（从队头到队尾元素递减）。队列中存储数组元素的索引，确保队头元素始终是当前窗口的最大值。通过动态调整队列，算法在 O(n) 时间内解决问题。

初始化队列（处理前k个元素）：

• 遍历前 k 个元素（索引 0 到 k-1）。
• 对于每个元素，从队列尾部开始，移除所有小于当前元素的索引（因为这些元素不可能成为最大值）。
• 将当前元素索引加入队列尾部。
• 此时队头即为第一个窗口的最大值。

处理剩余元素（窗口向右移动）：

• 从第 k 个元素（索引 k）开始遍历。
• 移除尾部较小元素：从队列尾部移除所有小于当前元素的索引（保证队列单调递减）。
• 加入新元素索引：将当前元素索引加入队列尾部。
• 移除过期队头：检查队头索引是否超出窗口左边界（i - k），若超出则移除（保证队头在窗口内）。
• 记录当前窗口最大值：队头索引对应的元素即为当前窗口最大值。

class Solution {// 主方法：计算滑动窗口最大值public int[] maxSlidingWindow(int[] nums, int k) {// 获取输入数组长度int n = nums.length;// 创建双端队列（Deque接口，LinkedList实现）// 存储数组索引（非元素值），用于维护窗口内最大值Deque<Integer> deque = new LinkedList<Integer>();// 初始化第一个窗口 [0, k-1]for (int i = 0; i < k; ++i) {// 维护队列单调性：从队尾移除比当前元素小的索引// 语法：!deque.isEmpty() - 检查队列非空// nums[i] >= nums[deque.peekLast()] - 比较当前元素与队尾索引对应元素while (!deque.isEmpty() && nums[i] >= nums[deque.peekLast()]) {deque.pollLast(); // 移除队尾元素}deque.offerLast(i); // 当前索引入队尾}// 创建结果数组（窗口数量 = n-k+1）int[] ans = new int[n - k + 1];// 获取第一个窗口的最大值（队头索引对应元素）ans[0] = nums[deque.peekFirst()]; // 处理后续窗口 [k, n-1]for (int i = k; i < n; ++i) {// 维护单调性：移除队尾小于当前元素的索引while (!deque.isEmpty() && nums[i] >= nums[deque.peekLast()]) {deque.pollLast();}deque.offerLast(i); // 新索引入队尾// 移除过期索引（超出窗口左边界 i-k）// 语法：deque.peekFirst() - 查看队头不删除while (deque.peekFirst() <= i - k) {deque.pollFirst(); // 移除队头元素}// 存储当前窗口最大值（队头索引对应元素）// i-k+1 是结果数组的索引（从0开始递增）ans[i - k + 1] = nums[deque.peekFirst()];}return ans; // 返回结果数组}
}

实际复杂度分析：遍历一次nums,最坏情况下队列中入队，出队，获取第一个/最后一个元素的次数均不大于n次，所以时间复杂度为O(n)。

生产者 - 消费者模型：用队列缓冲数据，平衡生产和消费速度。（在操作系统篇）

3. 数组的操作

二分查找：在有序数组中高效查找元素

数组旋转：将数组向右旋转k位（如[1,2,3,4,5]旋转 2 位变为[4,5,1,2,3]），考察空间复杂度优化（原地旋转）。

原地旋转数组：三次反转法

算法思路 

通过三次反转实现数组的原地旋转，无需额外空间：

1. 反转整个数组

2. 反转前 k 个元素

3. 反转剩余元素

步骤详解（以 [1,2,3,4,5] 旋转 2 位为例）

1. 整体反转 → [5,4,3,2,1]

2. 反转前 k 个 → [4,5,3,2,1]

3. 反转剩余元素 → [4,5,1,2,3]

class Solution {public void rotate(int[] nums, int k) {int n = nums.length;k %= n; // 处理 k > n 的情况// 三步反转法reverse(nums, 0, n - 1); // 反转整个数组reverse(nums, 0, k - 1); // 反转前 k 个reverse(nums, k, n - 1); // 反转剩余元素}// 反转数组指定区间private void reverse(int[] nums, int start, int end) {while (start < end) {// 交换首尾元素int temp = nums[start];nums[start] = nums[end];nums[end] = temp;// 移动指针start++;end--;}}
}

二维数组寻址：给定行优先存储的二维数组A[m][n]，计算A[i][j]的内存地址（公式：LOC(i,j) = LOC(0,0) + (i*n + j)*L，L为元素大小）。

三、特殊结构与优化

1. 栈的变种

单调栈：解决 “下一个更大元素” 问题（如数组[2,1,2]中，每个元素的下一个更大元素为[-,2,-]）。

示例：设计算法找到数组中每个元素右侧第一个比它大的元素，要求时间复杂度O(n)。

单调栈解决“下一个更大元素”问题

算法思路

使用单调递减栈（栈中元素从栈底到栈顶递减），从前往后遍历数组：

1. 栈中存储尚未找到下一个更大元素的索引

2. 遍历每个元素时：

   • 若栈非空且当前元素 > 栈顶元素 → 当前元素即为栈顶元素的下一个更大元素

   • 记录结果并弹出栈顶，直至当前元素 ≤ 栈顶元素

3. 将当前元素索引入栈

关键特性

• 单调性维护：栈中索引对应的元素值保持递减

• 时间复杂度：O(n)（每个元素入栈、出栈各一次）

• 空间复杂度：O(n)（最坏情况栈存储所有元素）

import java.util.Deque;
import java.util.ArrayDeque;
import java.util.Arrays;class Solution {public int[] nextGreaterElement(int[] nums) {int n = nums.length;int[] res = new int[n];        // 结果数组Arrays.fill(res, -1);           // 初始化为-1（表示无更大元素）Deque<Integer> stack = new ArrayDeque<>(); // 单调栈（存储索引）for (int i = 0; i < n; i++) {// 当前元素 > 栈顶元素 → 找到栈顶元素的下一个更大元素while (!stack.isEmpty() && nums[stack.peek()] < nums[i]) {int idx = stack.pop();  // 弹出栈顶索引res[idx] = nums[i];     // 记录结果}stack.push(i); // 当前索引入栈}return res;}
}

共享栈：两个栈共享一块内存空间，栈顶相向增长，提高空间利用率。

2. 队列的变种

双端队列（Deque）：允许两端插入和删除，考察输入 / 输出受限的双端队列的出队序列合法性。

示例：输入序列[1,2,3,4]，判断输出序列[4,2,1,3]能否由输出受限的双端队列产生（答案：可以，通过特定插入顺序实现）。

循环队列：实现入队和出队操作，重点考察指针更新（rear = (rear+1)%MaxSize）。

四、常见应用

栈相关：

题目：用栈实现队列（LeetCode 232）。232. 用栈实现队列 - 力扣（LeetCode）

思路：用两个栈inStack和outStack，入队时压入inStack，出队时若outStack为空则将inStack元素全部弹出到outStack，再弹出outStack栈顶。

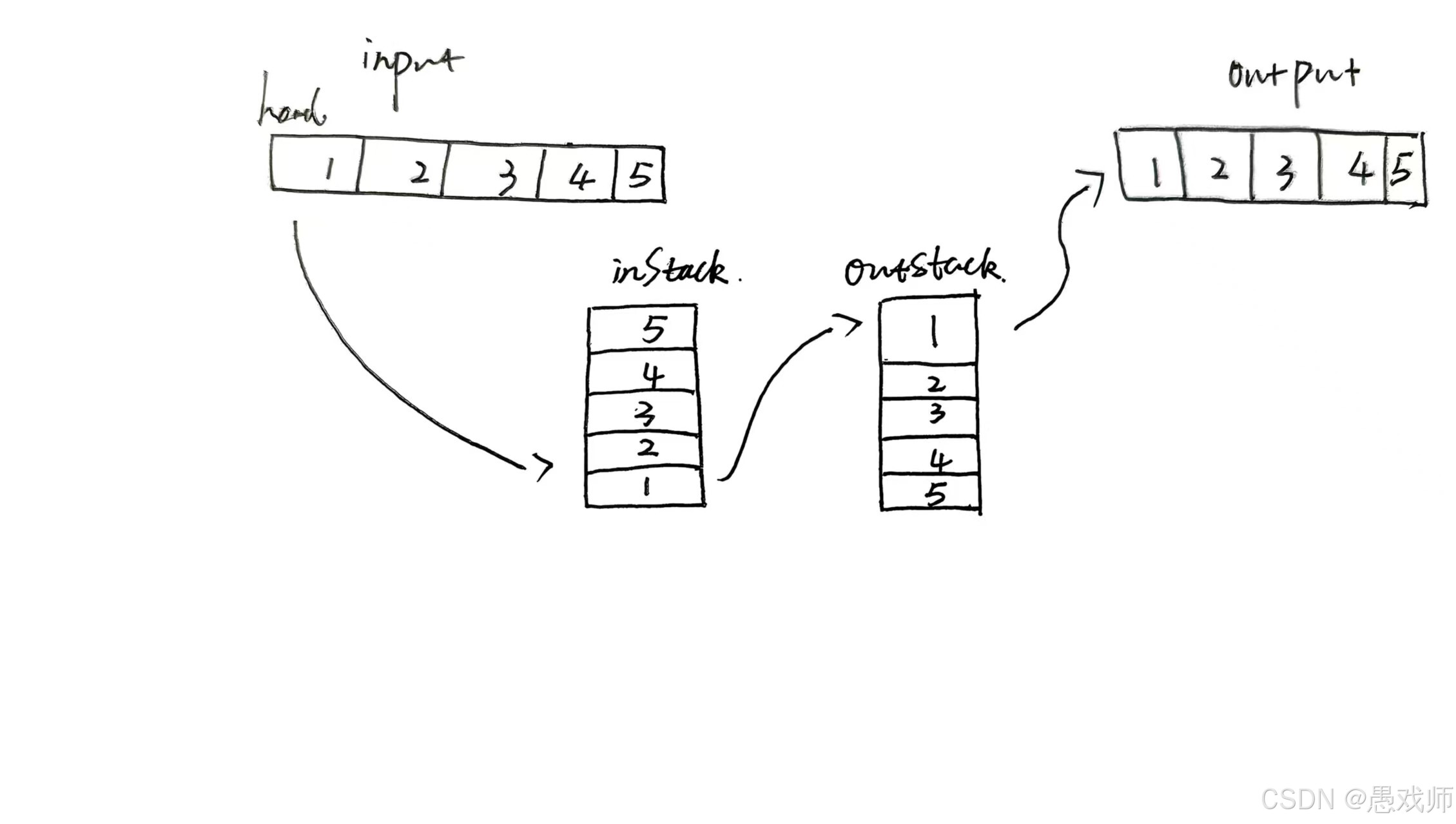
class MyQueue {private Deque<Integer> inStack;private Deque<Integer> outStack;public MyQueue() {inStack=new ArrayDeque<>();outStack=new ArrayDeque<>();}public void push(int x) {inStack.push(x);}public int pop() {if(outStack.isEmpty()){while(!inStack.isEmpty()){Integer x=inStack.pop();outStack.push(x);}}return outStack.pop();}public int peek() {if(outStack.isEmpty()){while(!inStack.isEmpty()){Integer x=inStack.pop();outStack.push(x);}}return outStack.peek();}public boolean empty() {return inStack.isEmpty() && outStack.isEmpty();}
}/*** Your MyQueue object will be instantiated and called as such:* MyQueue obj = new MyQueue();* obj.push(x);* int param_2 = obj.pop();* int param_3 = obj.peek();* boolean param_4 = obj.empty();*/

队列相关：

题目1：设计循环队列（LeetCode 622）。622. 设计循环队列 - 力扣（LeetCode）

实现：定义front、rear指针和容量，实现enQueue、deQueue、Front等方法，注意判空和判满条件。

设计思路：循环队列

循环队列使用固定大小的数组和两个指针（front 和 rear）来实现。关键点在于：

1. front 指向队列头部元素

2. rear 指向队列尾部元素的下一个位置

3. 通过取模操作实现指针循环

class MyCircularQueue {private int[] queue;     // 存储队列元素的数组private int front;       // 队首指针（指向第一个元素）private int rear;        // 队尾指针（指向下一个插入位置）private int capacity;    // 队列容量public MyCircularQueue(int k) {capacity=k+1;//循环队列预留一个位置判断是否满，所以容量为k+1queue=new int[capacity];front=rear=0;}public boolean enQueue(int value) {if((rear+1)%capacity==front)return false;queue[rear++]=value;return true;}public boolean deQueue() {if(rear==front)return  false;front++;return true;}public int Front() {if(isEmpty())return -1;return queue[front];}public int Rear() {if(isEmpty())return -1;return queue[rear-1];}public boolean isEmpty() {return rear==front;}public boolean isFull() {return (rear+1)%capacity==front;}
}/*** Your MyCircularQueue object will be instantiated and called as such:* MyCircularQueue obj = new MyCircularQueue(k);* boolean param_1 = obj.enQueue(value);* boolean param_2 = obj.deQueue();* int param_3 = obj.Front();* int param_4 = obj.Rear();* boolean param_5 = obj.isEmpty();* boolean param_6 = obj.isFull();*/

题目2：用队列实现栈。225. 用队列实现栈 - 力扣（LeetCode）

使用两个队列实现栈

设计思路

使用两个队列（queue1 和 queue2）模拟栈的后入先出特性：

1. 主队列：存储栈中所有元素

2. 辅助队列：在 push 操作时暂存元素

3. 核心操作：每次 push 新元素时，先将新元素放入辅助队列，再将主队列所有元素依次移入辅助队列，最后交换两个队列的角色,保证每次放入的元素都在主队列队首

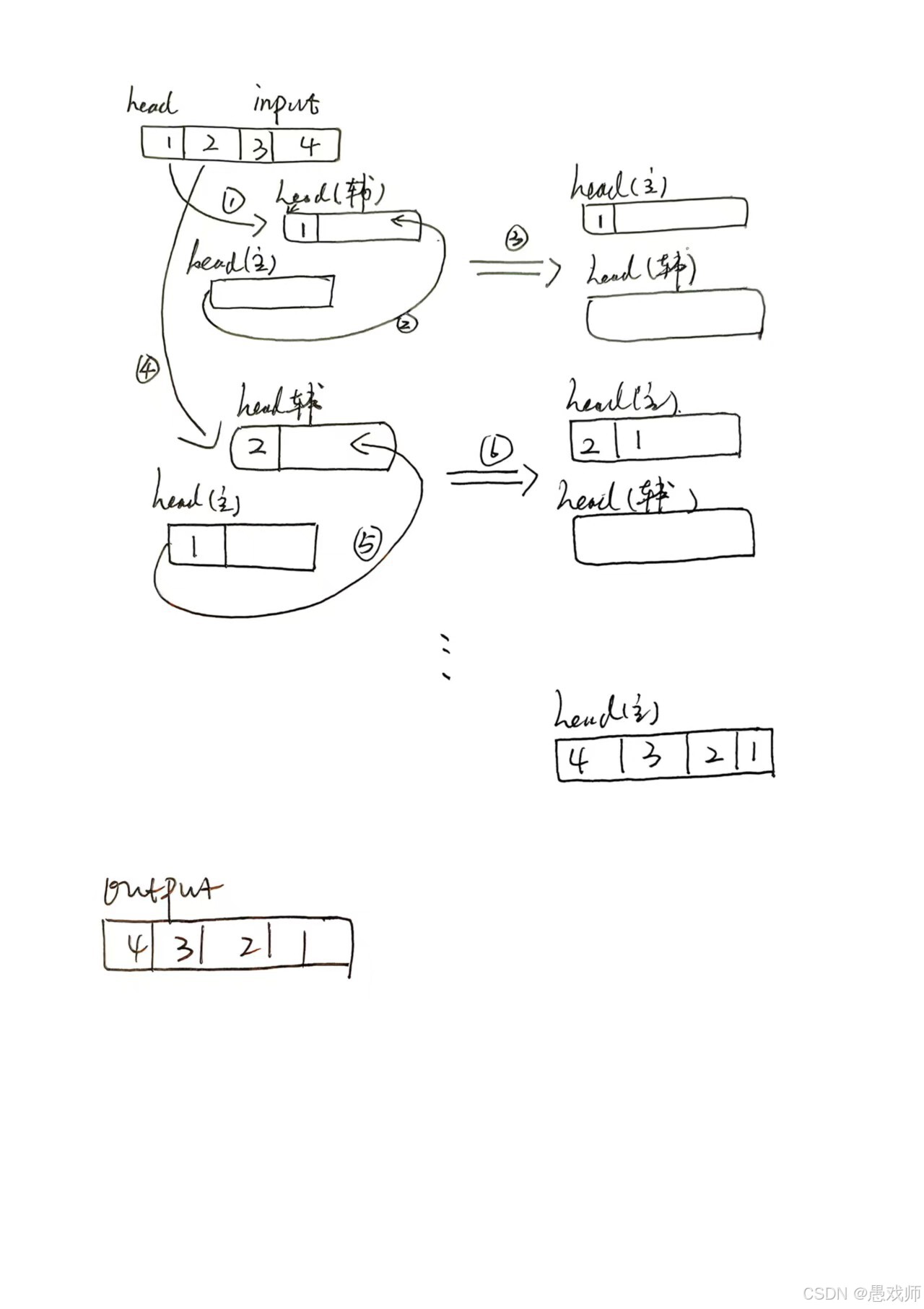
import java.util.LinkedList;
import java.util.Queue;class MyStack {private Queue<Integer> queue1;  // 主队列private Queue<Integer> queue2;  // 辅助队列public MyStack() {queue1 = new LinkedList<>();queue2 = new LinkedList<>();}// 将元素压入栈顶public void push(int x) {// 新元素先放入辅助队列queue2.offer(x);// 将主队列元素全部移入辅助队列while (!queue1.isEmpty()) {queue2.offer(queue1.poll());}// 交换两个队列的角色Queue<Integer> temp = queue1;queue1 = queue2;queue2 = temp;}// 移除并返回栈顶元素public int pop() {return queue1.poll();}// 返回栈顶元素（不移除）public int top() {return queue1.peek();}// 检查栈是否为空public boolean empty() {return queue1.isEmpty();}
}

数组相关： 

题目：找出数组中消失的数字（LeetCode 448）。448. 找到所有数组中消失的数字 - 力扣（LeetCode）

思路：遍历数组，将nums[i]对应的索引位置标记为负数，未标记的索引即为消失的数字。

class Solution {public List<Integer> findDisappearedNumbers(int[] nums) {List<Integer> ans=new ArrayList<>();for(int i=0;i<nums.length;i++){int index=Math.abs(nums[i])-1;if(nums[index]>0){nums[index]=-nums[index];}}for(int i=0;i<nums.length;i++){if(nums[i]>0)ans.add(i+1);}return ans;}
}