当前位置： 首页 > news >正文

01数据结构-平衡二叉树

news 2025/8/6 7:00:43

01数据结构-平衡二叉树

  • 前言
  • 1.二叉平衡树的概念
  • 2.二叉平衡树的插入
    • 2.1二叉平衡树的插入逻辑
    • 2.2二叉平衡树的插入代码
  • 3.二叉平衡树的删除
    • 3.1二叉平衡树的删除逻辑
    • 3.2二叉平衡树的删除代码
  • 4.平衡二叉树优缺点
    • 4.1优点
    • 4.2缺点
  • 5.任意树转二叉树

前言

前面我们介绍了二叉查找树，假设我们最开始送进去的序列就是有序的，那么会造成树往一边倒，如图1，树退化成了单链表，此时查找效率跟我们没有树的时候效率是一样的。那怎么在二叉搜索树的基础上让我们的高度可控，这就是我们今天增加的约束，增加完这个约束后就是我们今天讲的二叉平衡树。
图1
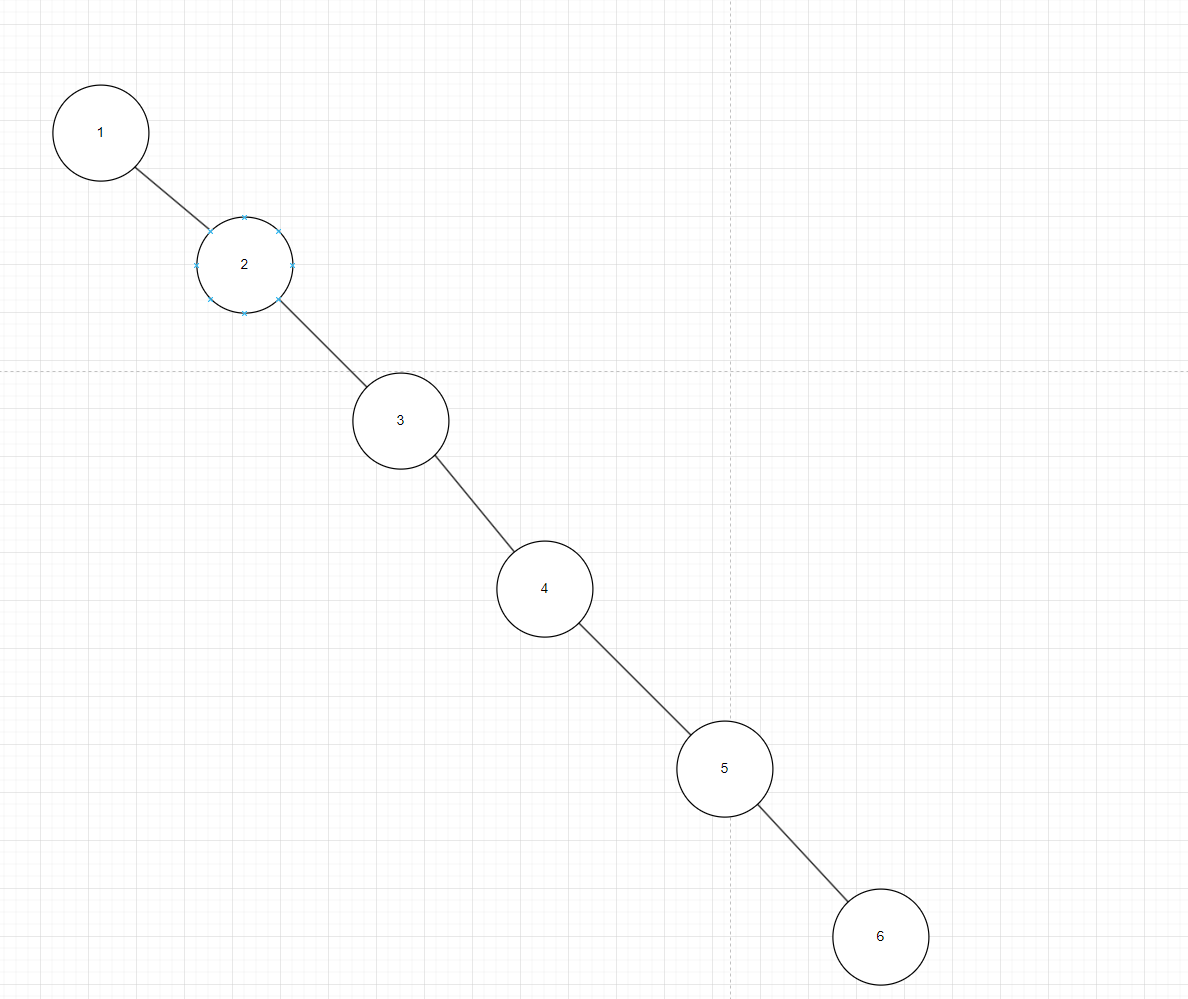
图1

1.二叉平衡树的概念

本身也就是二叉搜索树，在二叉搜索树的基础上给每个节点增加了平衡因子这个约束，平衡因子就是这个节点的左子树的高度减去右子树的高度的绝对值不能超过2。如图2，我们给每个节点增加一个高度元素，当某个节点的左右节点的高度相减的绝对值超过2，我们就认为该节点失衡，要对其进行平衡化。在这儿平衡的方法是旋转，在本节课的后面会介绍到。

图2
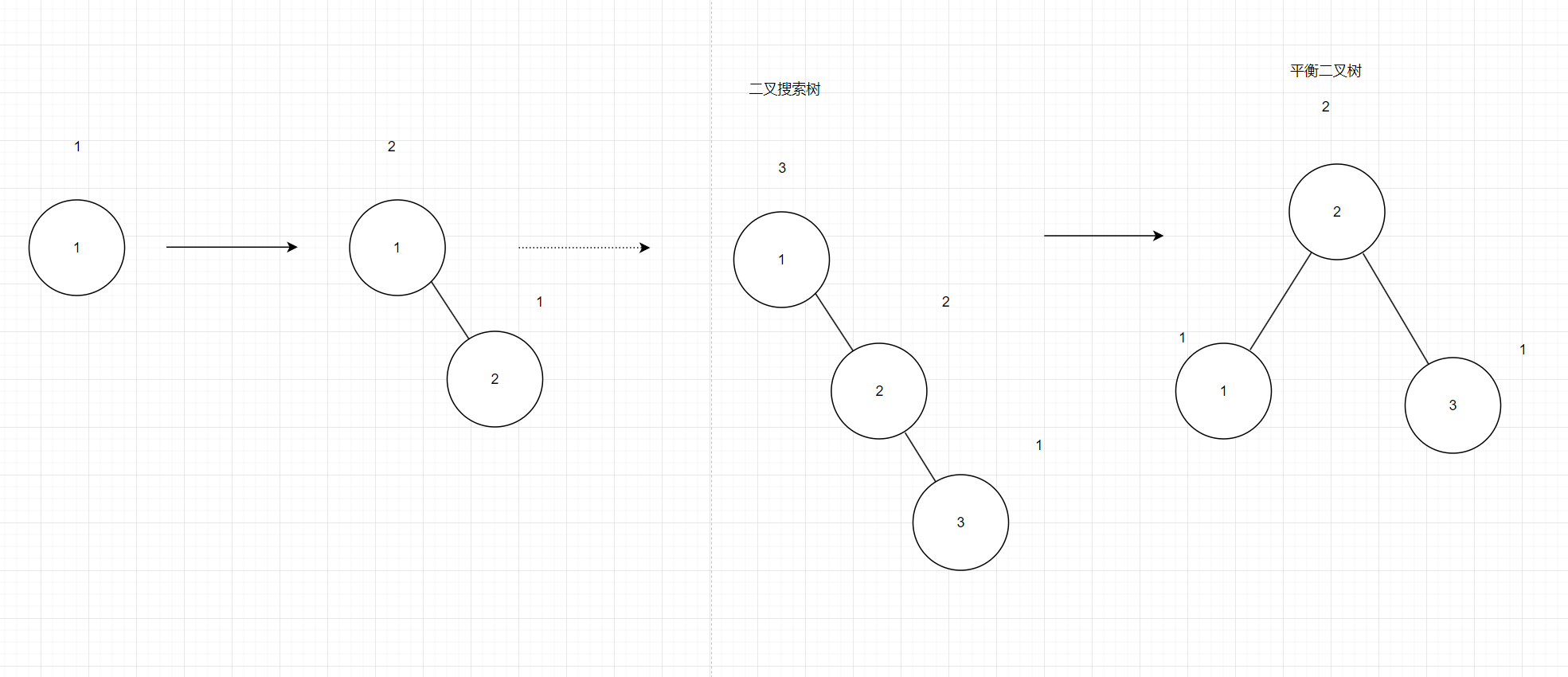
图2

2.二叉平衡树的插入

2.1二叉平衡树的插入逻辑

  • 按照二叉查找树的要求，放入新节点
  • 需要根据放入新节点的路径回溯，判断回溯中的节点是否出现失衡
  • 如果失衡，进行调整

如图3，插入元素8的之前，树中各个节点的元素都是平衡的，插入8时按照 右边标有颜色的路径递进去，先把8插到7的右节点，再从原路径归回来经过每一个节点的时候查看它的平衡因子，如果大于了2，就进行调整，此时途中失衡的点应该为6，我们就调整6的左右子树。下面我们介绍调整的方法，因为这个方法是前人已经总结归纳了的方法，这里我们就学会怎么用就行，暂时不用学怎么来的。
图3
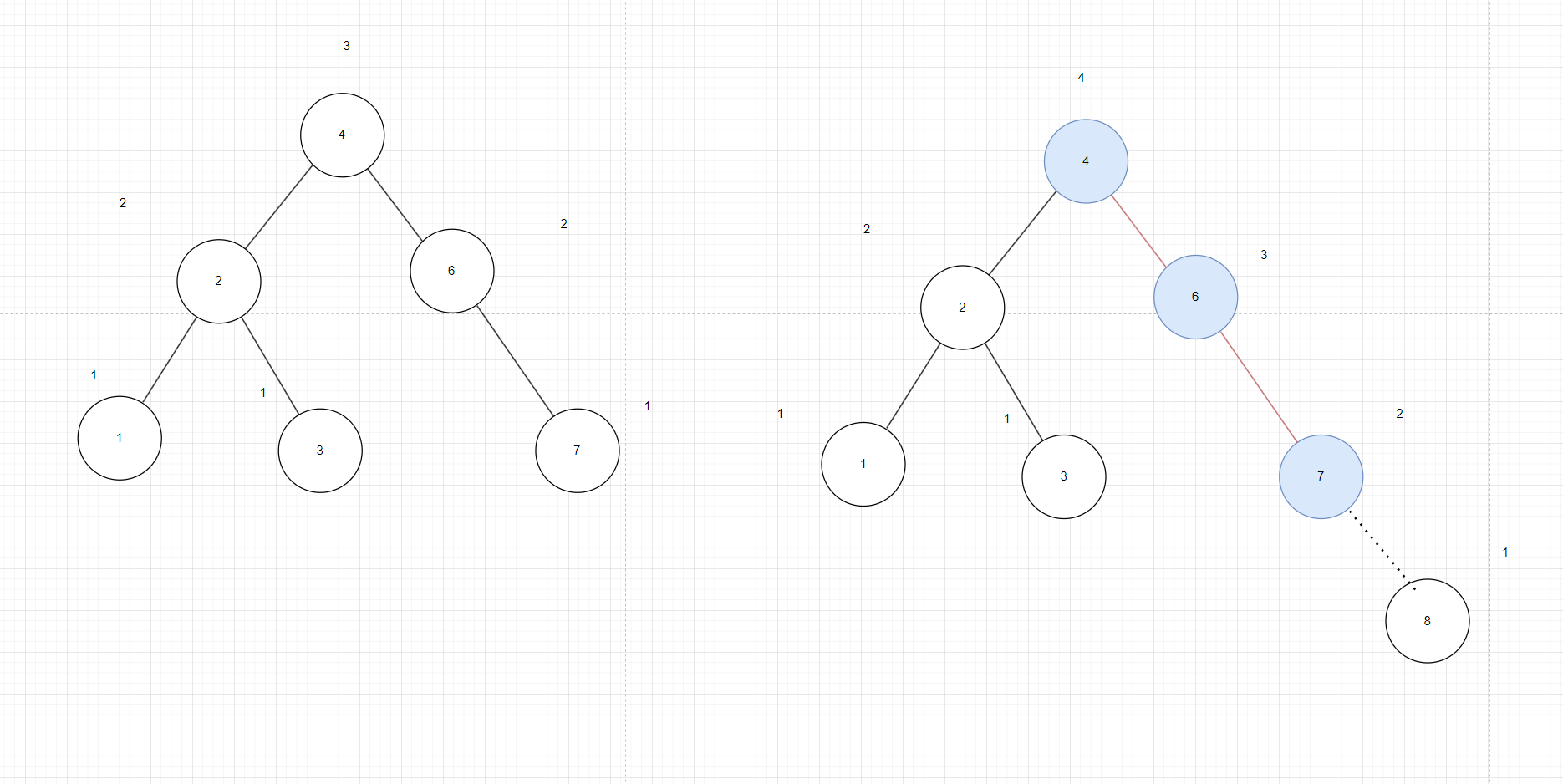
图3

调整方法：

  • 确定形式：LL,RR,LR,RL，第一个字母代表我们站在失衡点上我们是在哪个方向失衡的，第二个字母代表插入的节点在失衡点的子树的左边还是右边。
  • LL：失衡点右旋
    • 如图4，左边是原始平衡二叉树的结构，在插入30这个节点后，66失衡了，而站在失衡点，我们发现是由于左边太重了导致失衡所以第一个字母应该是L，又因为30插入在失衡点66的子树60（因为插入是从60进入的，所以这里选取的失衡点的子树应该是60）的左边，所以此时第二个字母也是L。LL你可以想象成左边太重了，右边有点轻，左边太重了，所以我们想到往右边偏一点。初中物理滑轮题大家都做过吧，滑轮左边的物体太重了相对于右边左边是压在下面的，这个时候借助滑轮可以让左边的物体上升一点，右边的物体下降一点。这里调整的方法也是这样

图4
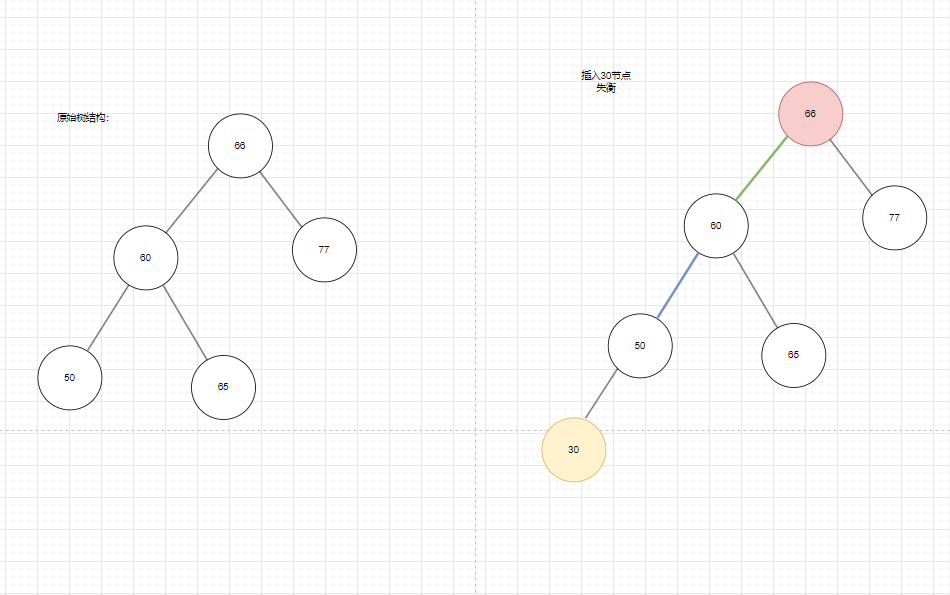
图4

  • 以失衡点66作为滑轮，往右边拽 ，77往下移动一层，66往下移动一层，60往上移动理论上60的右节点就是66了，但之前60的右节点没有进行处理，就出现了60有三个度的情况，不符合二叉树的特性，所以我们应该把一个节点连在另外一个节点上，此时把65连在66的左边问题就解决了，为什么要把65往66的左边连呢，因为在原始的树结构中，65本身就处于66的左边，现在由于66往下降了一层，60提上去了，因为是往右边拽动，所以60本身是被66管的（66的左节点60），往右拽了后60应该管66了（60的右节点66），拽了后66就没有左节点了因为原来的左节点已经拽上去，成为66的大哥了，那此时就把原来60的右节点连在66的左边。50往上升一层，30往上升一层平衡化就处理好了(总结：失衡点右旋)

图5
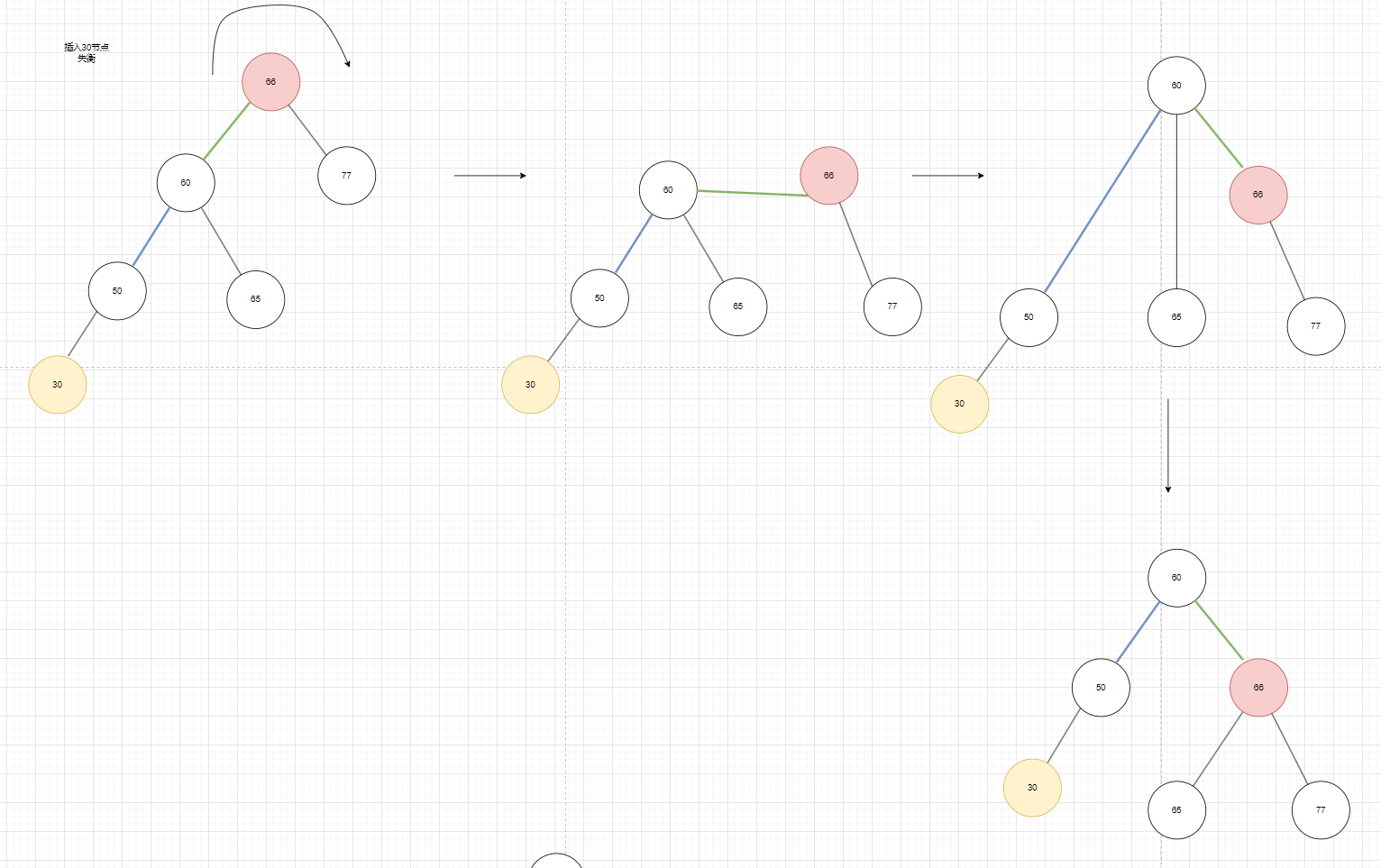
图5

如图6，也是LL类型，思路和图5一摸一样
图6
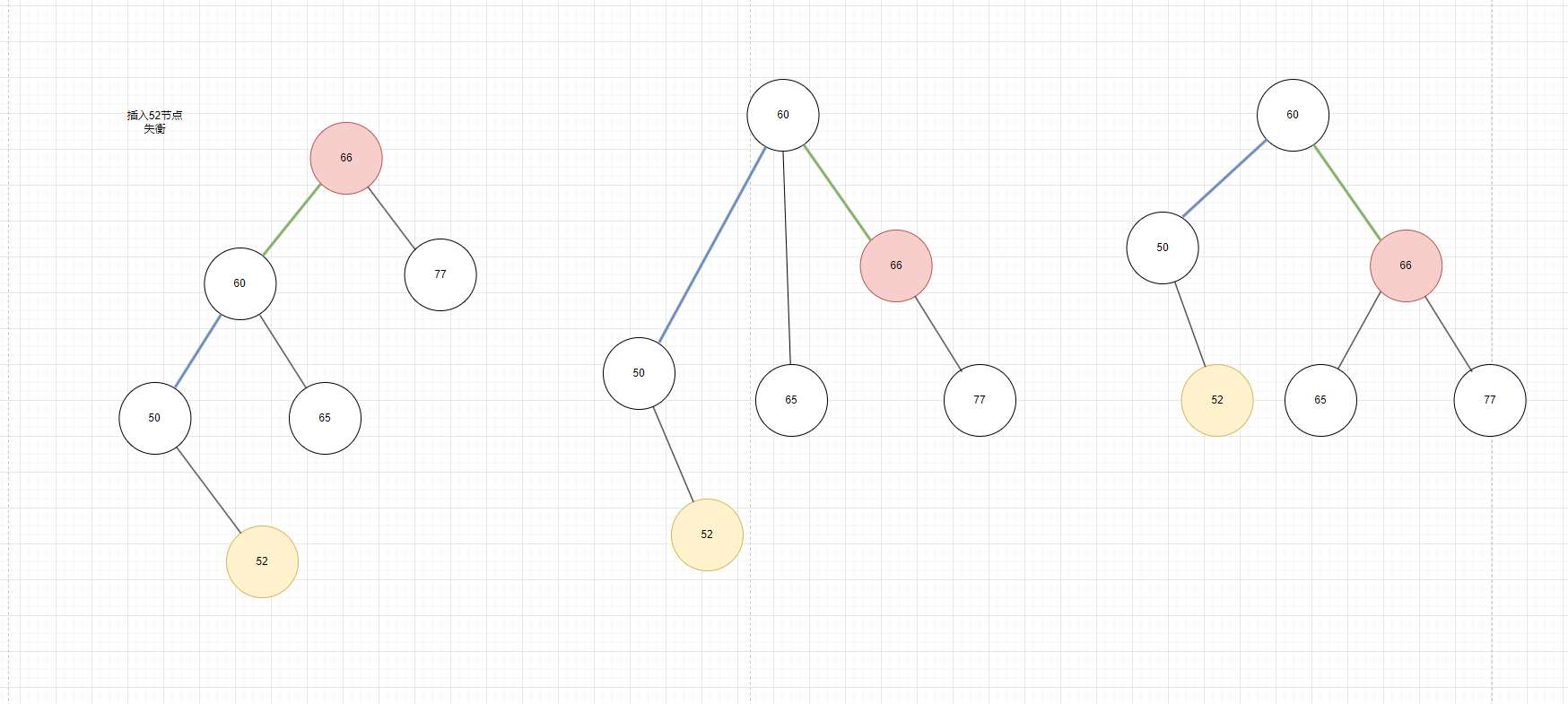
图6

  • LR:先右选再左旋

    • 先判断类型，发现66的左边过重且61插入在了60的右边属于LR类型，如果按照之前LL的算法如图7所示，依旧会失衡只不过失衡的节点从66换成了60且变成了右边很重，证明LR的处理逻辑和LL不相同，左边轻了，右边又重了。结合图6和图7可以看出，因为我们是将失衡点的节点的右子树直接给到的是右旋后的失衡点的左边的，失衡点的节点的左子树依旧连接在失衡点的节点的左边，因为失衡点的节点的右子树本身会连在下来了的失衡点所以层数并不会提高，失衡点的节点的左子树的层数因为右旋会提高。所以如果是LL，就是因为左边太重了，失衡点的节点的左子树的层数提高了，就平衡了，如果是LR失衡点的节点的右子树的层数不会提高，相反左边没那么重反而提高了，所以会造成左边太轻，右边太重了的情况。和二叉搜索树中的删除度为2节点的思想一样：转移矛盾。如果能想办法把LR转成LL再右旋一次不就行了吗下面来介绍怎么转移。
    • 我们要把LR的R变为L，我们以60（失衡点的子节点）为中心点进行左旋把右边的蓝色线拽到左边去不就变成LL了吗
      图7
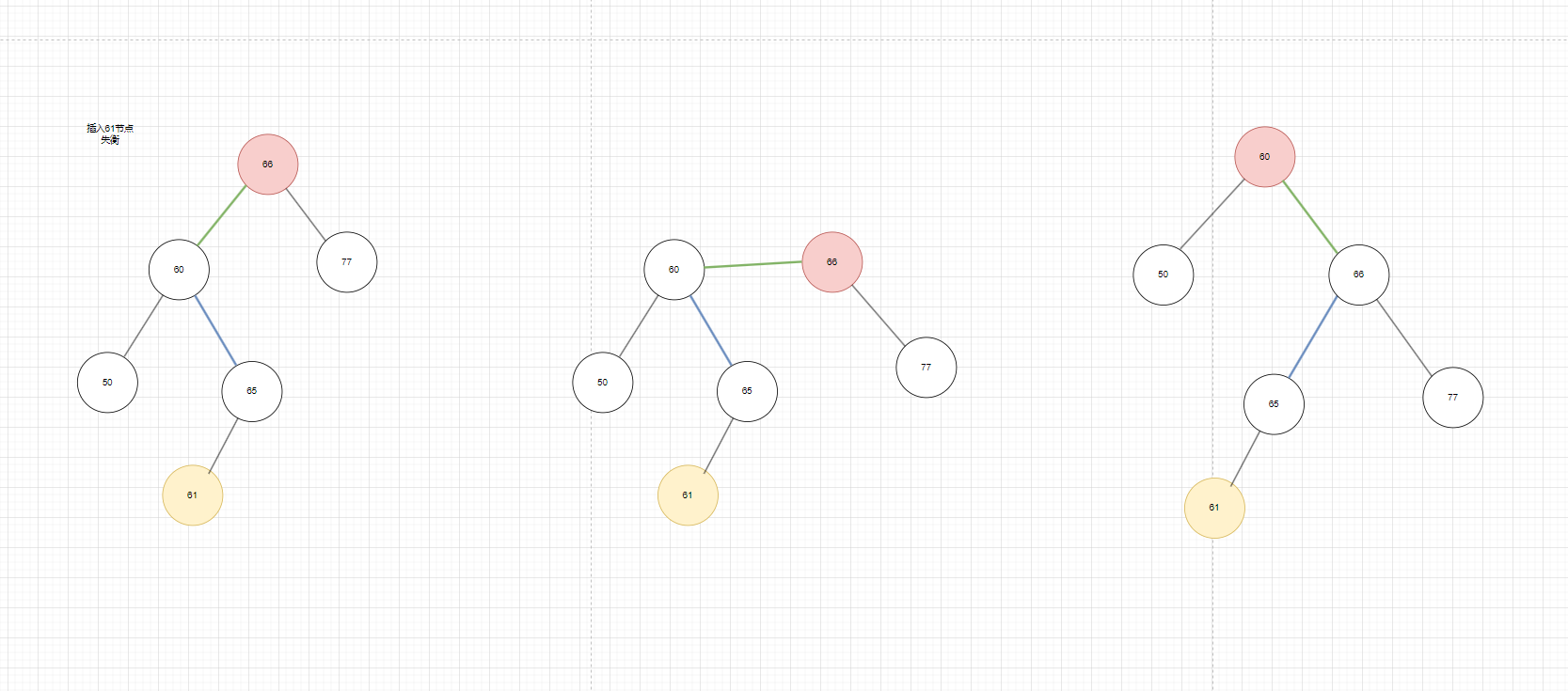
      图7

  • 先以60（失衡点的子节点）为中心点进行左旋，左旋的过程中，65的左节点会去连接60，所以原来的65的左节点61应该和65断开连接，然后连接到下来的60的右边再进行一次左旋即得到了最终平衡的树。有人可能会问，第一次旋转以后，不是有两个不平衡节点（65和66）吗？注意：LR双旋是一个完整的、原子性的再平衡操作，它解决一个特定的（LR型）不平衡点。在执行第一次旋转后不是引入了第二个新的不平衡点，而是原来的那个不平衡点仍存在，只是不平衡类型发生了变化(从LR变成了LL)，执行完第一次后的树只是临时状态，LR的两次旋转是连续的，执行完整个双旋后，该子树恢复平衡，且不会引入新的不平衡点。
    图8

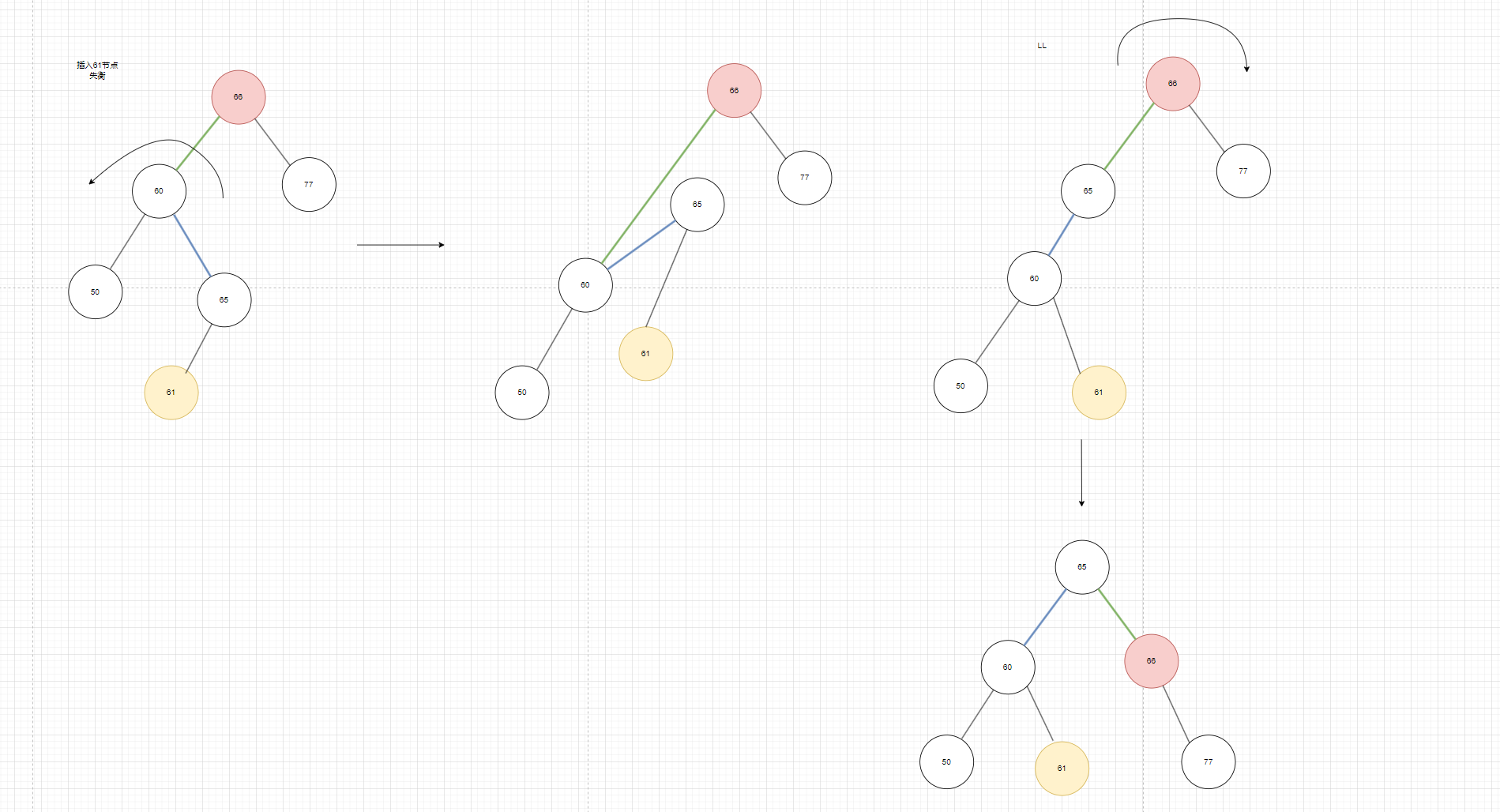
图8

  • 如图9，也是LR的类型但是在第一次旋转的时候62的左边为空，所以升上去去管理60的时候，62的左节点直接连接到60，而60的右节点依然是插入的63，再右旋一次即可。有人可能会问，新插入的节点63经过一次旋转后不还是在失衡点的子节点的右边吗?为什么却是LL类型，注意第一次旋转的核心在于改变树的不平衡结构，将LR类型转为LL类型，如果不把63当成新插入的节点，中间这棵树的不平衡类型就是LL。
    图9
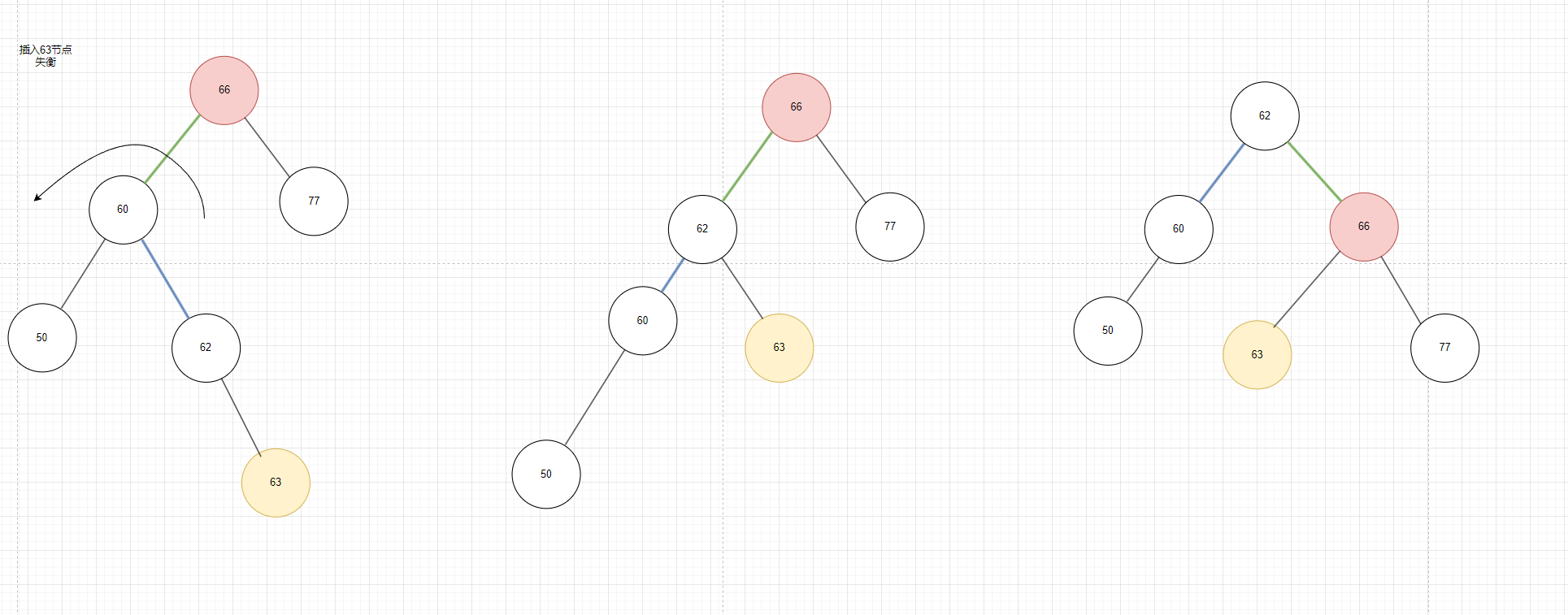
    图9

  • RR：失衡点左旋

    • RR的思路和LL是一样的，只不过因为右边太重把右旋改为左旋了，接下来看两个例子就行：这两个分别是连在最后一个节点的左边和右边
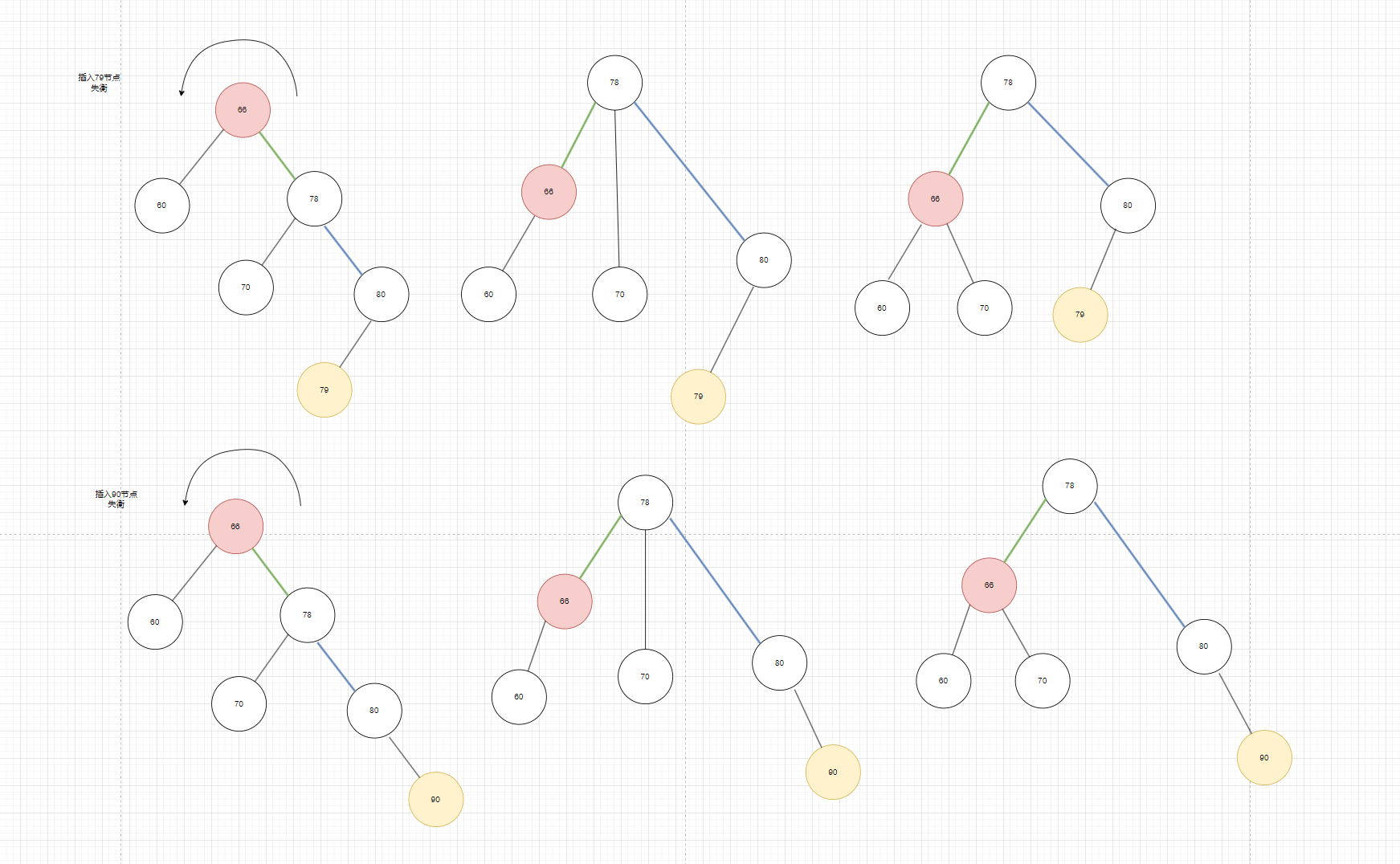
      图10
      图10

  • RL:先左选再右旋

    • RL的思路和LR是一样的，只不过先左旋再右旋，接下来看两个例子就行：这两个分别是连在最后一个节点的左边和右边
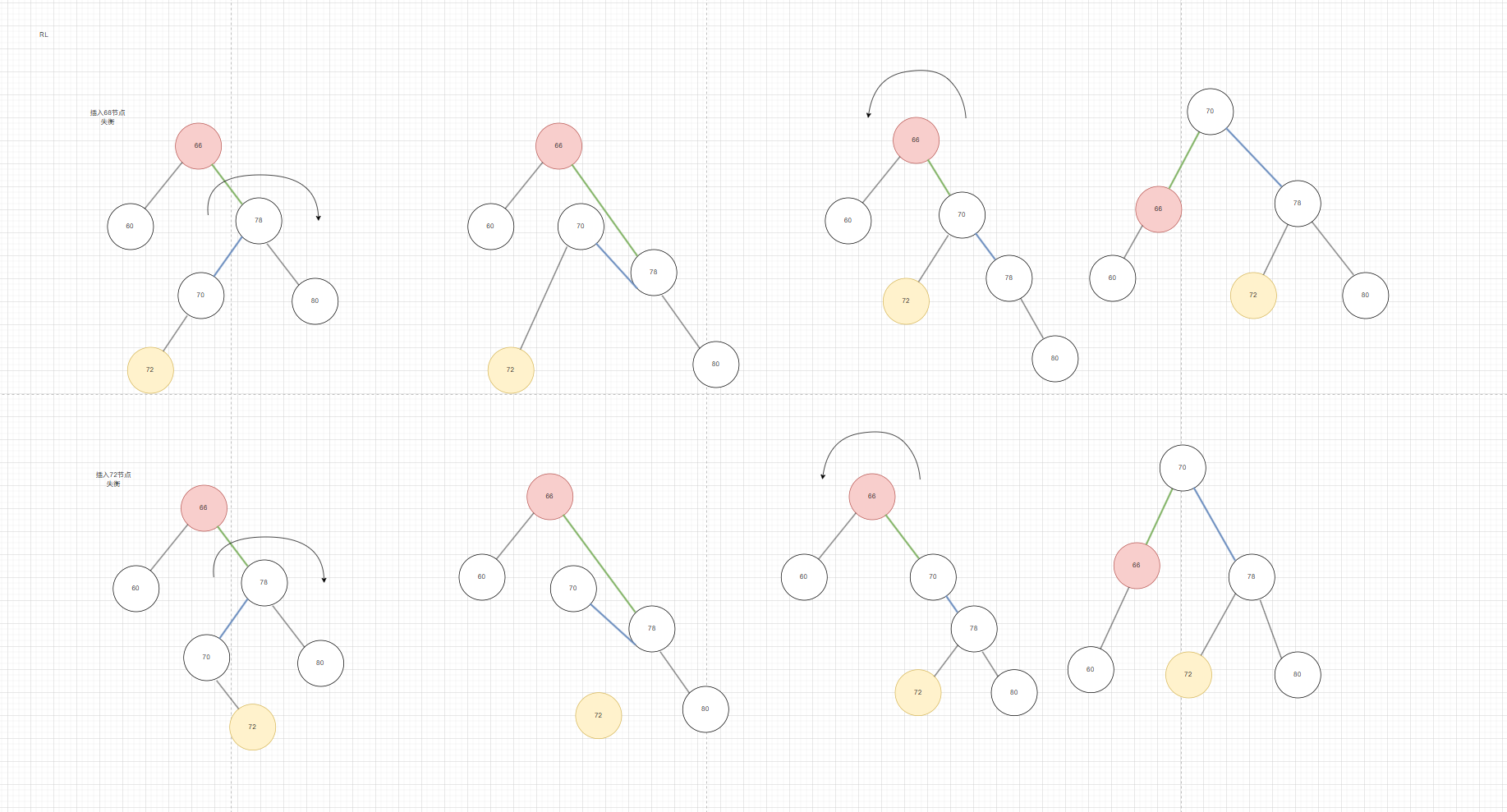
      图11
      图11

2.2二叉平衡树的插入代码

节点和树头的创建：

//定义节点结构
// 平衡二叉树的节点结构
typedef struct _avl_node {Element data;struct _avl_node *left, *right;int height;		// 当前节点的高度（这个节点左子树的高度和右子树高度的最大值 + 1）
} AVLNode;
// 平衡二叉树的树头结构
typedef struct {AVLNode *root;int count;
} AVLTree;

这里我给每个节点都设置一个高度，并在插入逻辑中更新节点的高度，就不用我们在二叉搜索树那里自己算高度了。

创建树头：AVLTree *createAVLTree();;

AVLTree * createAVLTree() {AVLTree * tree = malloc(sizeof(AVLTree));if (tree==NULL) {fprintf(stderr,"tree malloc failure!!!");return NULL;}tree->count=0;tree->root=NULL;return tree;
}

处理节点逻辑(这里是访问):void visitAVLNode(const AVLNode *node);

void visitAVLNode(const AVLNode* node) {if (node) {printf("\t<%d:%d>", node->data, node->height);}
}

把每个节点的高度打出来才知道是不是平衡二叉树

中序遍历：void inOrderAVLTree(AVLTree* tree);

static void inOrderNode(AVLNode *node) {if (node) {inOrderNode(node->left);visitAVLNode(node);inOrderNode(node->right);}
}void inOrderAVLTree(AVLTree* tree) {if (tree) {inOrderNode(tree->root);printf("\n");}
}

节点的高度:static int heightAVLNode(const AVLNode *node);

static int heightAVLNode(const AVLNode *node) {if (node) {return node->height;} else {return 0;}
}

树的高度：int heightAVLTree(const AVLTree* tree) ;

int heightAVLTree(const AVLTree* tree) {if (tree) {return tree->root->height;}return 0;
}

创建节点：static AVLNode * createAVLNode(Element data);

static AVLNode * createAVLNode(Element data) {AVLNode *new_node=malloc(sizeof(AVLNode));if (new_node==NULL) {fprintf(stderr,"new_node malloc failure!!!");return NULL;}new_node->data=data;new_node->left=NULL;new_node->right=NULL;new_node->height=1;return new_node;
}

把节点的高度设为1。

释放节点的接口和释放树:static void freeAVLNode(AVLTree *tree, AVLNode *node) ;

//释放节点
static void freeAVLNode(AVLTree *tree, AVLNode *node) {if (node) {freeAVLNode(tree, node->left);freeAVLNode(tree, node->right);free(node);tree->count--;}
}
//释放树
void releaseAVLTree(AVLTree* tree) {if (tree) {freeAVLNode(tree, tree->root);printf("There are %d nodes.\n", tree->count);free(tree);}
}

因为在等会的插入代码中会更新节点的高度，所以不用像之前一样，写一个static内在接口函数自己算节点的高度，然后传根节点算树的高度了，这里直接返回树的根节点的高度即可。
——————————————————————————————————————
咱先来看一下插入代码整体框架的思路：

static AVLNode* insertAVLNode(AVLTree *tree,AVLNode *node,Element data) {// 1. 递归的初始化位置//递归终止条件if (node==NULL) {tree->count++;return createAVLNode(data);}// 1.1 递的过程if (data < node->data) {node->left=insertAVLNode(tree, node->left, data);}else if (data>node->data) {node->right=insertAVLNode(tree, node->right, data);}else {return node;}// 2. 运行到这里的代码，已经进入到归的过程，更新这条路径上节点高度，同时监测平衡因子// 2.1 归过程中的节点高度的更新node->height = 1 + max(heightAVLNode(node->left), heightAVLNode(node->right));// 2.2 计算机当前节点的平衡因子int balance = getBalance(node);if (balance > 1) {// 失衡点子节点是L还是R，LL or LRif (data > node->left->data) {// LRnode->left = leftRotate(node->left);}// LLreturn rightRotate(node);}if (balance < -1) {if (data < node->right->data) {// RLnode->right = rightRotate(node->right);}// RRreturn leftRotate(node);}return node;
}void insertAVLTree(AVLTree *tree, Element data) {if (tree) {tree->root = insertAVLNode(tree, tree->root, data);}
}

我主要讲2，也就是归回来的部分。

  • 由于我给每个节点都设置了高度，所以在归回来的过程中需要实时更新每个节点的高度，而节点的高度是左右子树的最大值加上它本身的一个1，所以我们需要定义一个max函数来返回两者之间的较大值

用于返回左右子树中较高的树：static int max(int a,int b);

static int max(int a,int b) {return a>=b?a:b;
}
  • 处理完高度的问题后，我们需要对创建一个临时变量平衡因子，用来计算左右子树的差的绝对值是否大于大于1，所以我们需要定义一个getBalance函数来返回节点的左右子树的高度差值：
    返回节点的左右子树的高度差值：static int getBalance(const AVLNode *node);
static int getBalance(const AVLNode *node) {return heightAVLNode(node->left)-heightAVLNode(node->right);
}
  • 得到平衡因子后，我们需要判断是哪种失衡类型：LL? LR? RR? RL? 如果平衡因子大于1结合static int getBalance(const AVLNode *node) 说明左子树比右子树重，说明第一个字母是L，如果data > node->left->data说明第二个字母是R，此时应该先左旋node->left，再右旋node，如果否直接右旋node;如果平衡因子小于-1结合static int getBalance(const AVLNode *node) 说明右子树比左子树重，说明第一个字母是R，如果data < node->right->data说明第二个字母是L，此时应该先右旋node->right，再左旋node，如果否直接左旋node，我们单独把左右旋封装成一个函数。我们单独把左右旋封装成一个函数。

左旋：static AVLNode *leftRotate(AVLNode *x);

/* 左旋操作*     px*     |*     x*   /  \* lx    y*      / \*     ly ry* */
static AVLNode *leftRotate(AVLNode *x) {AVLNode *y=x->right;x->right=y->left;y->left=x;x->height = 1 + max(heightAVLNode(x->left), heightAVLNode(x->right));y->height = 1 + max(heightAVLNode(y->left), heightAVLNode(y->right));return y;
}

看注释里面的图，我们需要把y的左边交给x，还需要把x的左边交给y，如果只是直接写

x->right=x->right->left;
x->right->left=x;

在执行第一话的时候x->right已经是ly，执行第二句话会出错，这是因为没有备份x->right导致我们第二次找不到图中y的地址了，所以用我们前面讲的备份思想，第一句话先将x->right备份到y，然后第二句话就可以修改x->right了，将y->left交给x->right，这样y->left相当于也备份了，在第三句话就能改y->left了。注意旋转后x和y的高度发生了变化，ly,ry,lx并没有都是1，所以需要重新计算x和y的高度，这里必须先算x->height，因为旋转后x是在下面，我们的计算方法是左右子树高度的最大值+1，要先更新下面的值。如果先更新y的值，y由于是在x的上方，此时x的高度没有更新，依旧是旋转前的高度3，就会出错。所以要先更新旋转后节点在下方的点。

右旋：static AVLNode *rightRotate(AVLNode *y);

/* 右旋操作*       py*       |*       y*     /  \*    x   ry*   / \* lx  rx* */
static AVLNode *rightRotate(AVLNode *y) {AVLNode *x=y->left;y->left=x->right;x->right=y;y->height = 1 + max(heightAVLNode(y->left), heightAVLNode(y->right));x->height = 1 + max(heightAVLNode(x->left), heightAVLNode(x->right));return x;
}

思路和左旋一样只是方向变了，我就不过多叙述。

  • 注意旋转过后的值要返给对应的节点。以便于归回去的时候更新。

最后来测一下：

#include <stdio.h>
#include "avlTree.h"void test01() {AVLTree *tree = createAVLTree();Element data[] = {10, 20, 30, 40,50, 60, 68, 80,25, 7, 55};for (int i = 0; i < sizeof(data)/sizeof(data[0]); ++i) {insertAVLTree(tree, data[i]);}printf("InOrder: ");inOrderAVLTree(tree);printf("Tree Height: %d\n", heightAVLTree(tree));}int main() {test01();return 0;
}

结果：

D:\work\DataStruct\cmake-build-debug\02_TreeStruct\AVLTree.exe
InOrder:        <7:1>   <10:2>  <20:3>  <25:1>  <30:2>  <40:4>  <50:2>  <55:1>  <60:3>  <68:2>  <80:1>
Tree Height: 4进程已结束，退出代码为 0

3.二叉平衡树的删除

3.1二叉平衡树的删除逻辑

二叉平衡树的删除逻辑和二叉搜索树的删除逻辑差不多，只不过在归回来的过程中需要像上面插入逻辑归回来时一样需要对每个节点进行高度调整，并对需要做出平衡的节点根据其类型进行旋转。二叉搜索树的删除逻辑详情可以看《01数据结构-二叉搜索树》，附上链接：https://blog.csdn.net/2302_82136376/article/details/149856849?fromshare=blogdetail&sharetype=blogdetail&sharerId=149856849&sharerefer=PC&sharesource=2302_82136376&sharefrom=from_link

3.2二叉平衡树的删除代码

二叉平衡树删除代码

static AVLNode *deleteAVLNode(AVLTree* tree,AVLNode *node,Element e) {if (node == NULL) {return NULL;}//递if (e<node->data) {node->left=deleteAVLNode(tree, node->left, e);}else if (e>node->data) {node->right=deleteAVLNode(tree, node->right, e);}//找到元素判断度为0或1或2的节点分别处理else {AVLNode *temp;if (node->left == NULL || node->right == NULL) {temp = node->left ? node->left : node->right;if (temp == NULL){// 度为0，直接删除tree->count--;free(node);return NULL;}// 度为1，将tmp的值直接替换成nodenode->data = temp->data;node->left = temp->left;node->right = temp->right;tree->count--;free(temp);return node;}temp = node->left;while (temp->right) {temp = temp->right;}node->data = temp->data;node->left = deleteAVLNode(tree, node->left, temp->data);}//归node->height=max(heightAVLNode(node->left),heightAVLNode(node->right))+1;int balance = getBalance(node);//Lif (balance>1) {//LRif (e>node->left->data) {node->left=leftRotate(node->left);}return rightRotate(node);}//Rif (balance < -1) {//RLif (e<node->right->data) {node->right=rightRotate(node->right);}return leftRotate(node);}return node;
}void deleteAVLTree(AVLTree *tree, Element e) {if (tree) {tree->root = deleteAVLNode(tree, tree->root, e);}
}

这里有区别于前面的是这里的处理：按照之前的写也可以（注释里面的代码）

  AVLNode *temp;if (node->left == NULL || node->right == NULL) {temp = node->left ? node->left : node->right;if (temp == NULL){// 度为0，直接删除tree->count--;free(node);return NULL;}// 度为1，将tmp的值直接替换node//<----retrurn node的过程----->node->data = temp->data;node->left = temp->left;node->right = temp->right;tree->count--;free(temp);}//  AVLNode *temp;//if (node->left==NULL) {//temp = node->right;//free(node);//--tree->count;//return temp;//}//else if (node->right==NULL) {// temp = node->left;// free(node);//--tree->count;//return temp;
//}

最后测一下：

#include <stdio.h>
#include "avlTree.h"void test01() {AVLTree *tree = createAVLTree();Element data[] = {10, 20, 30, 40,50, 60, 68, 80,25, 7, 55};for (int i = 0; i < sizeof(data)/sizeof(data[0]); ++i) {insertAVLTree(tree, data[i]);}printf("InOrder: ");inOrderAVLTree(tree);printf("Tree Height: %d\n", heightAVLTree(tree));printf("InOrder: ");deleteAVLTree(tree, 60);inOrderAVLTree(tree);releaseAVLTree(tree);
}int main() {test01();return 0;
}

结果：

D:\work\DataStruct\cmake-build-debug\02_TreeStruct\AVLTree.exe
InOrder:        <7:1>   <10:2>  <20:3>  <25:1>  <30:2>  <40:4>  <50:2>  <55:1>  <60:3>  <68:2>  <80:1>
Tree Height: 4
InOrder:        <7:1>   <10:2>  <20:3>  <25:1>  <30:2>  <40:4>  <50:1>  <55:3>  <68:2>  <80:1>
There are 0 nodes.进程已结束，退出代码为 0

4.平衡二叉树优缺点

4.1优点

优点：查找非常快(静态操作)

4.2缺点

缺点：增加，删除慢(动态操作)因为需要调平等操作。

5.任意树转二叉树

这里补充一个知识点任意树转二叉树的方法：孩子兄弟表示法

将一般的树转换为二叉树，可以遵循以下规则：

  • 树中每个节点的第一个子节点作为转换后二叉树节点的左子节点。
  • 树中每个节点的右兄弟节点作为转换后二叉树节点的右子节点。

如图12按照上述规则对给定的树进行转换：

1.对于节点A，它的第一个子节点是B，所以B成为二叉树中A的左子节点；A的右兄弟节点不存在。然后看B，B没有子节点，B的右兄弟节点是C，所以C成为二叉树中B的右子节点。

2.对于C，它的第一个子节点是E，所以E成为二叉树中C的左子节点，C的右兄弟节点是D，所以D成为二叉树中C的右子节点；D的第一个子节点不存在，D的右兄弟节点也不存在。

3.对于C的另一个子节点F，它是E的兄弟节点，所以F成为二叉树中E的右子节点。

图12
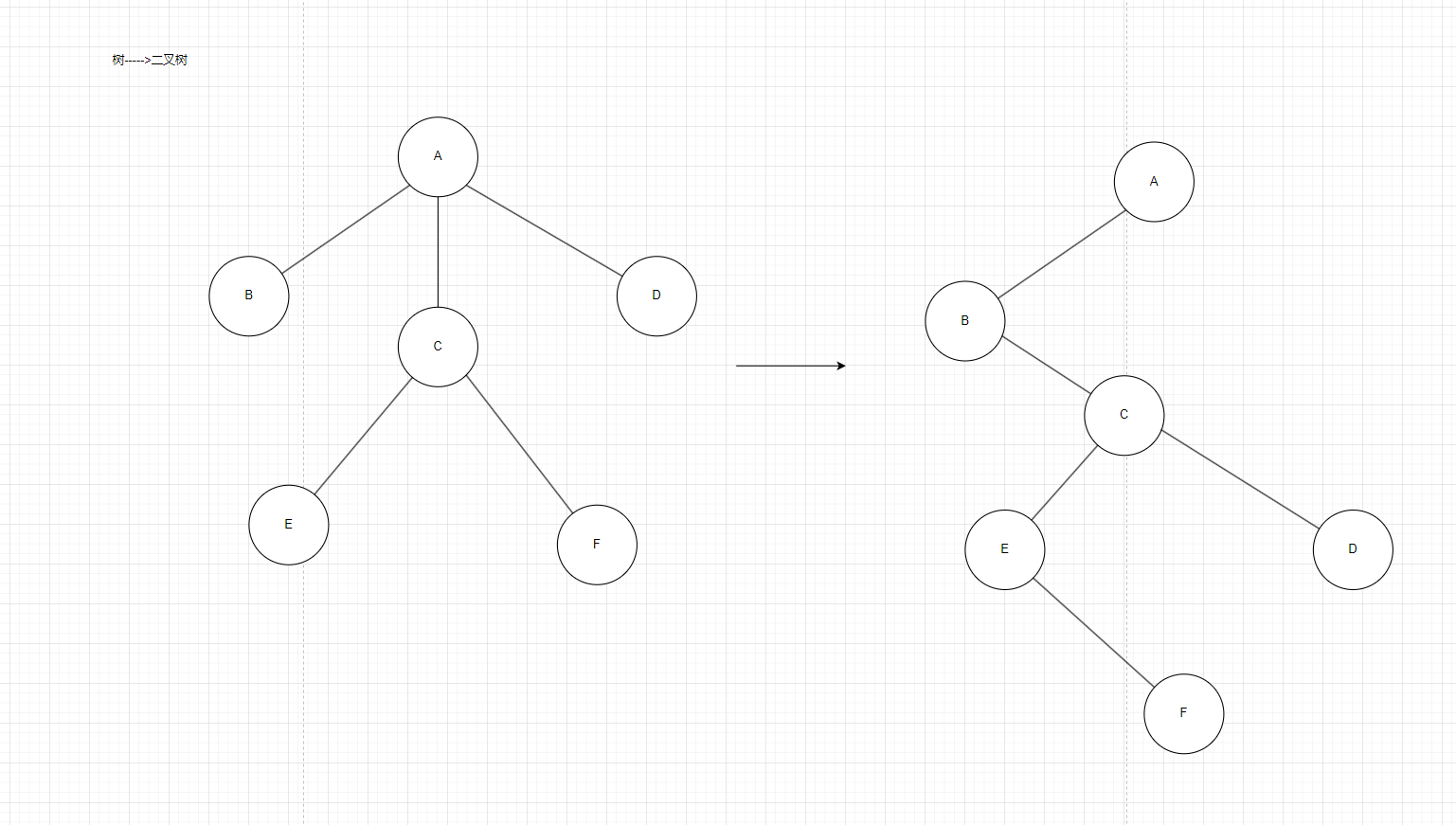
图12

二叉树转任意树的方法把上面的方法倒过来即可，我就不过多叙述。

大概先写这些吧，今天的博客就先写到这，谢谢您的观看。

http://www.dtcms.com/a/315425.html

相关文章：

  • Prometheus监控学习-安装
  • 【Git】实现使用SSH方式连接远程仓库时的免密操作
  • 计算机网络：目的网络在路由表项中的作用
  • Python实战项目--学生成绩管理系统
  • 机器人slam个人笔记
  • 交叉验证：机器学习模型评估的“稳压器”——从原理到实战
  • 测试开发：Python+Django实现接口测试工具
  • AI 对话高效输入指令攻略（四）：AI+Apache ECharts：生成各种专业图表
  • 第六章 道阻且艰（2025.7学习总结）
  • 期权定价全解析：从Black-Scholes到量子革命的金融基石
  • 利用Coze平台生成测试用例
  • 发票的分类识别与查验接口-发票管理软件-发票查验API
  • C++返回值优化（RVO）：高效返回对象的艺术
  • 《算法导论》第 2 章 - 算法基础
  • spring webflux链路跟踪【traceId日志自动打印】
  • 【Spring Boot 快速入门】七、阿里云 OSS 文件上传
  • 从零实现富文本编辑器#6-浏览器选区与编辑器选区模型同步
  • dos中常用的全屏幕编辑器
  • 一次“无告警”的服务器宕机分析：从无迹可寻到精准定位
  • 服务器数据恢复—坏道致Raid5阵列硬盘离线如何让数据重生？
  • 【Electron】electron-vite中基于electron-builder与electron-updater实现程序远程自动更新，附源码
  • 前端性能工程化：构建高性能Web应用的系统化实践
  • 8.5 CSS3-flex弹性盒子
  • 从达梦到 StarRocks：国产数据库实时入仓实践
  • NFS CENTOS系统 安装配置
  • RAGFlow 0.20.0 : Multi-Agent Deep Research
  • Java Date类介绍
  • 计算机网络：（十三）传输层（中）用户数据报协议 UDP 与 传输控制协议 TCP 概述
  • Python 基础语法（二）：流程控制语句详解
  • FPGA实现Aurora 8B10B视频点对点传输，基于GTP高速收发器，提供4套工程源码和技术支持