OpenCV学习 day4

一、图像梯度处理

1、图像梯度

把图像想象成连续函数，因为边缘部分的像素值是与旁边像素值有明显区别的，所以对图片局部求极值，就可以得到整幅图像的边缘信息了。不过图像是二维的离散函数，导数就变成了差分，这个差分就成为图像的梯度。

图像梯度表示的是图像中像素强度的变化率（即“变化有多快”），用于检测边缘、轮廓和纹理。它本质是图像的一阶导数，其中包含着两个关键信息：

• 1、梯度大小：变化的强度（边缘的明显程度）。
• 2、梯度方向：变化的方向（边缘的朝向）。

2、垂直边缘提取

垂直边缘的检测依赖于 水平梯度（Gx），即对图像在 x方向（水平） 的变化率进行卷积计算。

核心思想：

• 垂直边缘是图像中 水平方向像素值的突变（如从黑到白的过渡）。
• 通过设计特定的水平梯度卷积核（Gx），可以增强垂直边缘的响应。

API:

cv2.filter2D(src, ddepth, kernel)

filter2D函数是用于对图像进行二维卷积（滤波）操作。它允许自定义卷积核（kernel）来实现各种图像处理效果，如平滑、锐化、边缘检测等

参数：

• src：输入的图像，一般为numpy数组。
• ddepth：输出图像的深度，可以是负值（表示与原图相同）、正值或者其他特定的值（常用-1表示输出与输入具有相同的深度）。
• kernel：卷积核，一个二维数组（通常为奇数大小的方形矩阵），用于计算每个像素周围领域的加权和

数组模拟:

import cv2 as cv
import numpy as np
# 模拟一张图像，灰度图
img=np.array([[100,102,109,110,98,20,19,18,21,22],[109,101,98,108,102,20,21,19,20,21],[109,102,105,108,98,20,22,19,19,18],[109,98,102,108,102,20,23,19,20,22],[109,102,105,108,98,20,22,19,20,18],[100,102,108,110,98,20,19,18,21,22],[109,101,98,108,102,20,22,19,20,21],[109,102,108,108,98,20,22,19,19,18],],dtype=np.float32)
# 定义卷积核，
kernel=np.array([[-1,0,1],[-2,0,2],[-1,0,1]],dtype=np.float32)
# 二维卷积操作
img2=cv.filter2D(img,-1,kernel)
# 打印卷积后的图
print(img2)

3、Sobel算子

水平梯度卷积核（Gx）（用于检测垂直边缘）：
$$G_x^{}=\left[\begin{array}{ccc}-1& 0& 1\\ -2& 0& 2\\ -1& 0& 1\end{array}\right]$$

• 作用：中间列权重更大，增强对噪声的鲁棒性
• 特点：平滑（加权平均） + 差分（边缘检测）

API：

sobel_image = cv2.Sobel(src, ddepth, dx, dy, ksize)

参数：

• src：输入图像，通常应该是一个灰度去向（单通道图像）
• ddepth：代表输出图像的深度，即输出图像的数据类型。常用-1表示输出图像与输入图像的深度相同。
• dx，dy：当组合为dx=1,dy=0时求x方向的一阶导数，在这里，设置为1意味着我们想要计算图像在水平方向（x轴）的梯度。当组合为 dx=0,dy=1时求y方向的一阶导数
• ksize：Sobel算子的大小，可选择3、5、7，默认为3.

OpenCV代码实现

import cv2 as cv#读图，灰度化
img = cv.imread("../../images/shudu.png", cv.IMREAD_GRAYSCALE)
cv.imshow("img", img)#dx=1:水平方向上差分求梯度，提取的是垂直边缘
dst=cv.Sobel(img,-1,1,0,ksize=3)
cv.imshow("dst",dst)# dy=1:垂直方向上差分求梯度，提取的是水平边缘
dst2=cv.Sobel(img,-1,0,1,ksize=3)
cv.imshow( "dst2",dst2)#dx,dy都等于1，两个方向上差分求梯度，这个算子通常不会得到想要的结果
dst3=cv.Sobel(img,-1,1,1,ksize=3)
cv.imshow("dst3",dst3)cv.waitKey(0)
cv.destroyAllWindows()

处理结果：
原图：

水平方向差分求梯度，提取的是垂直边缘：

垂直方向上差分求梯度，提取的是水平边缘：

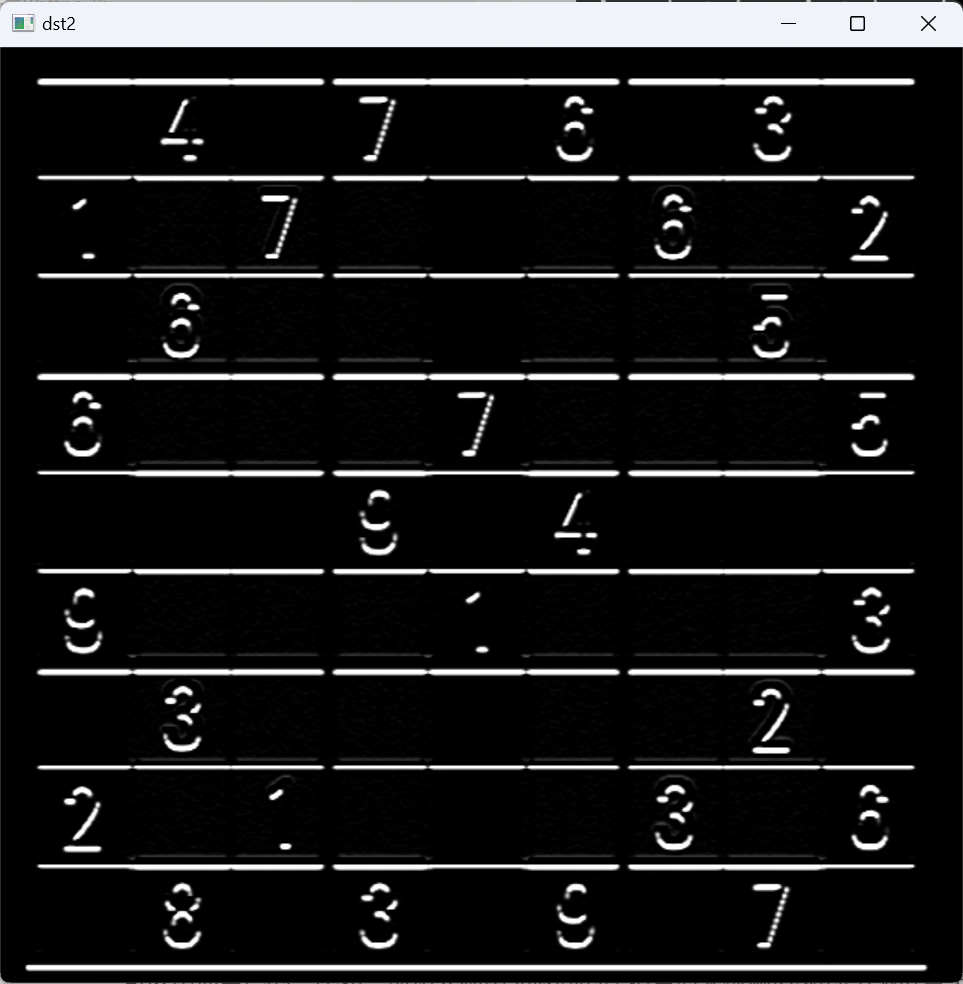
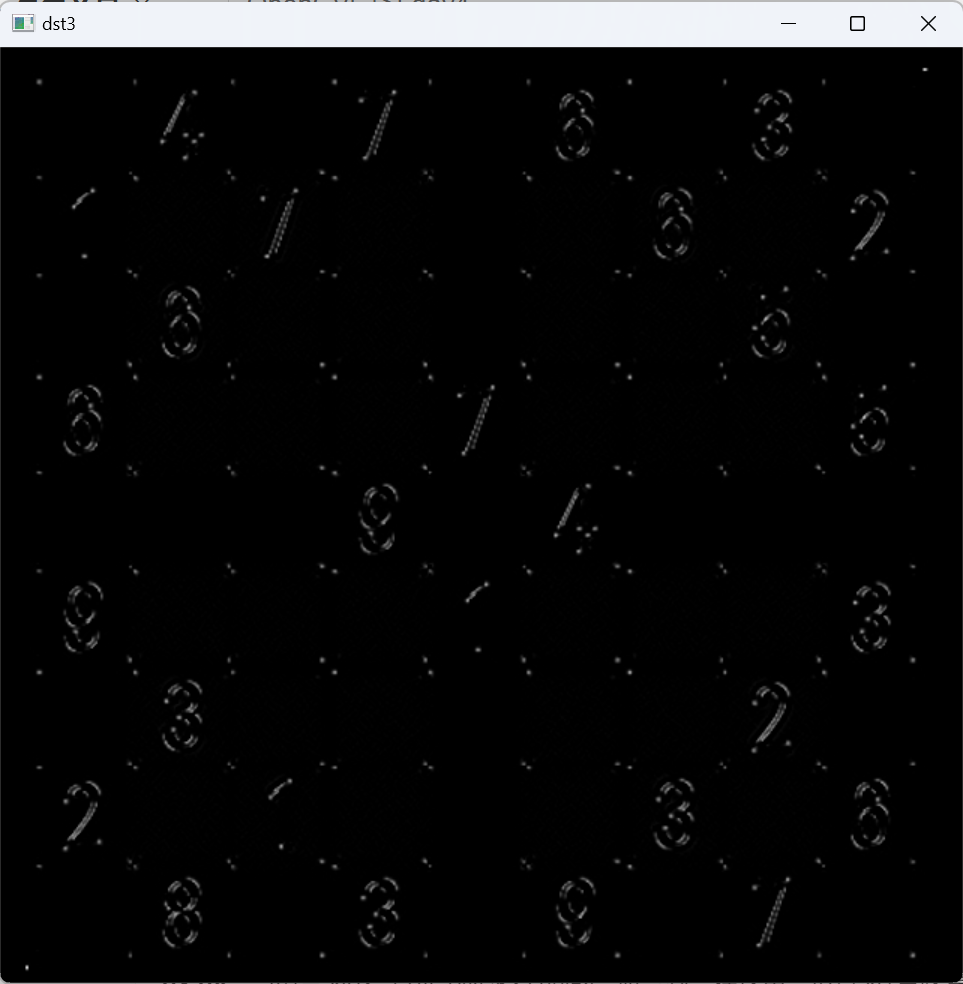
两个方向上差分梯度：

4、Laplacian算子

常用的3×3Laplacian卷积核有两种形式：

四领域：
$$\left[\begin{array}{ccc}0& 1& 0\\ 1& -4& 1\\ 0& 1& 0\end{array}\right]$$

八领域
$$\left[\begin{array}{ccc}1& 1& 1\\ 1& -8& 1\\ 1& 1& 1\end{array}\right]$$
八邻域对斜向边缘更敏感，但噪声响应也更强。

Laplacian算子的特点：

二阶微分： 直接检测像素强度的“变化率的变化”，对边缘和角点敏感。
对噪声敏感 会放大高频噪声，通常需先高斯模糊（即 LoG 算子）。
各向同性： 对水平、垂直、斜向边缘的响应相同（旋转不变性）。

OpenCV代码实现

import cv2 as cv#读图
shudu = cv.imread("../../images/shudu.png", cv.IMREAD_GRAYSCALE)
cv.imshow("shudu", shudu)#使用Laplacian算子提取边缘（输出为 CV_64F）
dst = cv.Laplacian(shudu, cv.CV_64F)
cv.imshow("dst", dst)# 取绝对值并转为 CV_8U（0~255）
dst1 = cv.convertScaleAbs(dst)
cv.imshow("dst1", dst1)cv.waitKey(0)
cv.destroyAllWindows()

Laplacian算子是二阶边缘检测的典型代表，一/二阶边缘检测各有优缺点，大家可自行了解。

5、Laplacian 与 Sobel 对比

对比项	Laplacian	Sobel
阶数	二阶导数	一阶导数
边缘响应	过零点（Zero-Crossing）	极值点
方向性	各向同性（无方向偏好）	分水平/垂直方向
噪声敏感度	更高（需高斯平滑）	较低
适用场景	边缘增强、锐化、斑点检测	通用边缘检测

二、图像边缘检测

图像边缘检测不是一个算子，而是完整的一整套方案。

边缘检测是图像处理中的核心任务，用于识别图像中物体边界或显著变化区域。其核心思想是检测像素强度的突变（比如从黑到白的过度）。

高斯滤波处理：
就是去除噪点！
边缘检测本身属于锐化操作，对噪点比较敏感，所以一般需要进行平滑处理。

1、边缘检测的核心原理

(1) 边缘的数学定义

• 一阶导数极值：边缘对应像素强度函数的一阶导数的极大值点（如Sobel检测）。
• 二阶导数过零点：边缘对应二阶导数的零交叉点（如Laplacian检测）。

(2) 边缘类型

类型	特点
阶跃边缘	像素值突然变化（如黑白交界）
斜坡边缘	像素值渐变（模糊边缘）
屋顶边缘	像素值先增后减（细线）

2、经典边缘检测算法

(1) 一阶微分算子

① Sobel 算子

• 原理：加权差分（平滑噪声 + 增强边缘）。
• 卷积核：
  $G_x^{}=\left[\begin{array}{ccc}-1& 0& 1\\ -2& 0& 2\\ -1& 0& 1\end{array}\right]$，$G_y^{}=\left[\begin{array}{ccc}-1& -2& -1\\ 0& 0& 0\\ 1& 2& 1\end{array}\right]$

② Prewitt 算子

• 特点：简单差分，抗噪性弱于Sobel。
• 卷积核：
  $G_x^{}=\left[\begin{array}{ccc}-1& 0& 1\\ -1& 0& 1\\ -1& 0& 1\end{array}\right]$，$G_y^{}=\left[\begin{array}{ccc}-1& -1& -1\\ 0& 0& 0\\ 1& 1& 1\end{array}\right]$

③ Roberts 算子

• 特点：检测对角线边缘，对噪声敏感。
• 卷积核：
• $G_x^{}=\left[\begin{array}{cc}0& 1\\ -1& 0\end{array}\right]$，$G_y^{}=\left[\begin{array}{cc}1& 0\\ 0& -1\end{array}\right]$

(2) 二阶微分算子

① Laplacian 算子

• 原理：直接计算二阶导数，突出快速变化区域。
• 卷积核：
  $$\left[\begin{array}{ccc}0& 1& 0\\ 1& -4& 1\\ 0& 1& 0\end{array}\right]$$

② LoG（Laplacian of Gaussian）

步骤：先高斯模糊再Laplacian，减少噪声影响。

(3) Canny 边缘检测（最优算法）

流程：

• 1、高斯滤波去噪
• 2、计算梯度幅值和方向（Sobel）
• 3、非极大值抑制（细化边缘）
• 4、双阈值检测（强边缘+弱边缘连接）

优势：抗噪性强，边缘连续且细。

3. 算法对比与选择

算法	优点	缺点	适用场景
Sobel	计算快，抗噪较好	边缘较粗	实时检测
Prewitt	简单	噪声敏感	高对比度图像
Laplacian	各向同性	噪声敏感	锐化、斑点检测
Canny	边缘细、连续，抗噪强	计算复杂	高精度边缘检测

4、Canny的API和使用

即使读到的是彩色的图也可以进行处理。
返回值edges，边缘检测后的结果

edges = cv2.Canny(image, threshold1, threshold2)

参数：

• image：输入的灰度/二值化图像数据。
• threshold1：低阈值，用于决定可能的边缘点。
• threshold2：高阈值，用于决定强边缘点。

OpenCV代码实现

import cv2 as cv#读图,并且灰度化处理
shudu = cv.imread("../../images/shudu.png",cv.IMREAD_GRAYSCALE)
cv.imshow("shudu",shudu)#Canny边缘检测
edged = cv.Canny(shudu,30,70)#显示效果
cv.imshow("edged",edged)
cv.waitKey(0)
cv.destroyAllWindows()

三、绘制图像轮廓

轮廓是一系列相连的点组成的曲线，代表了物体的基本外形。相对于边缘，轮廓是连续的，边缘不一定连续，如下图所示。轮廓是一个闭合的、封闭的形状。

轮廓的作用：

• 形状分析
• 目标识别
• 图像分割

1、基本流程

步骤概括：

• 1、边缘检测：使用Canny、阈值法等提取边缘。
• 2、 轮廓查找：cv2.findContours() 获取轮廓列表。
• 3、轮廓绘制：cv2.drawContours() 在原图上绘制轮廓。

2、AIP与使用

contours,hierarchy = cv2.findContours(image，mode，method)

参数：

• 返回值：contours：轮廓点坐标；hierarchy：层级关系。
• contours：表示获取到的轮廓点的列表。检测到有多少个轮廓，该列表就有多少子列表，每一个子列表都代表了一个轮廓中的所有点的坐标。
• hierarchy：表示轮廓之间的关系。
• image：表示输入的二值化图像。
• mode：表示轮廓的检索模式。
• method：轮廓的表示方法。

（1）mode参数

轮廓查找方式。返回不同的层级关系。

mode参数共有四个选项分别为：RETR_LIST，RETR_EXTERNAL，RETR_CCOMP，RETR_TREE。

①RETR_EXTERNAL

表示只查找最外层的轮廓。并且在hierarchy里的轮廓关系中，每一个轮廓只有前一条轮廓与后一条轮廓的索引，而没有父轮廓与子轮廓的索引。

2.3.4.会查找所有轮廓，但会有层级关系。

②RETR_LIST

表示列出所有的轮廓。并且在hierarchy里的轮廓关系中，每一个轮廓只有前一条轮廓与后一条轮廓的索引，而没有父轮廓与子轮廓的索引。

③RETR_CCOMP

表示列出所有的轮廓。并且在hierarchy里的轮廓关系中，轮廓会按照成对的方式显示。

在 RETR_CCOMP 模式下，轮廓被分为两个层级：

• 层级 0：所有外部轮廓（最外层的边界）。
• 层级 1：所有内部轮廓（孔洞或嵌套的区域）。

④RETR_TREE

表示列出所有的轮廓。并且在hierarchy里的轮廓关系中，轮廓会按照树的方式显示，其中最外层的轮廓作为树根，其子轮廓是一个个的树枝。

（2）method参数

轮廓存储方法。轮廓近似方法。决定如何简化轮廓点的数量。就是找到轮廓后怎么去存储这些点。

method参数有三个选项：CHAIN_APPROX_NONE、CHAIN_APPROX_SIMPLE、CHAIN_APPROX_TC89_L1。

• CHAIN_APPROX_NONE表示将所有的轮廓点都进行存储
• CHAIN_APPROX_SIMPLE表示只存储有用的点，比如直线只存储起点和终点，四边形只存储四个顶点，默认使用这个方法；

常用：对于mode和method这两个参数来说，一般使用RETR_EXTERNAL和CHAIN_APPROX_SIMPLE这两个选项。

（3）使用

OpenCV代码实现

import cv2 as cv
#读图
img = cv.imread("../../images/666.png")
img1 = cv.resize(img,(300,300))#灰度化
gray = cv.cvtColor(img1, cv.COLOR_BGR2GRAY)#二值化
thresh , binary = cv.threshold(gray, 127, 255, cv.THRESH_OTSU + cv.THRESH_BINARY_INV)
print(thresh)
cv.imshow("binary", binary)#查找轮廓
conts,hie = cv.findContours(binary,cv.RETR_EXTERNAL,cv.CHAIN_APPROX_SIMPLE)
print(f"轮廓数量：{len(conts)}")
print(conts)
print("--------------------------------------------------------")
print(hie)#绘制轮廓
img2 = cv.drawContours(img1,conts,-1,(255,0,0),2)
cv.imshow("img2",img2)#显示效果cv.waitKey(0)
cv.destroyAllWindows()

四、凸包特征检测

凸包是计算几何中的经典概念，在图像处理中用于简化轮廓形状、分析物体凸性缺陷（如凹陷区域）或提取拓扑结构。以下是OpenCV中的实现方法和应用场景。

1、凸包的定义

• 数学定义：包含给定点集的最小凸多边形。
• 直观理解：用橡皮筋包围所有点时的形状（无凹陷）。
• 关键特性：
  • 凸包上的任意两点连线均在多边形内部。
  • 用于区分物体的凸性（如区分手掌张开和握拳）。

2、OpenCV中的凸包计算

（1）获取凸包点

cv2.convexHull(points)

• points：输入参数，图像的轮廓点

（2）绘制凸包

cv2.polylines(image, pts, isClosed, color, thickness=1)

参数：

• image：要绘制线条的目标图像，它应该是一个OpenCV格式的二维图像数组（如numpy数组）。
• pts：一个二维 numpy 数组，每个元素是一维数组，代表一个多边形的一系列顶点坐标。
• isClosed：布尔值,表示是否闭合多边形,如果为 True，会在最后一个顶点和第一个顶点间自动添加一条线段，形成封闭的多边形。
• color：线条颜色，可以是一个三元组或四元组，分别对应BGR或BGRA通道的颜色值，或者是灰度图像的一个整数值。
• thickness（可选）：线条宽度，默认值为1。

(3)OpenCV代码实现

import cv2 as cv
#读图
img = cv.imread("../../images/666.png")
img1 = cv.resize(img,(300,300))#灰度化
gray = cv.cvtColor(img1, cv.COLOR_BGR2GRAY)
cv.imshow("gray", gray)#二值化
_, binary = cv.threshold(gray,127,255,cv.THRESH_OTSU + cv.THRESH_BINARY_INV)
print(f"合理阈值{_}")
cv.imshow("binary",binary)#查找轮廓 counts:轮廓点，hie:层级关系
counts , hie = cv.findContours(binary,cv.RETR_EXTERNAL,cv.CHAIN_APPROX_SIMPLE)
print(f"轮廓数量{len(counts)}")
print(counts)
print("------------------------------------------")
print(hie)#绘制轮廓
cv.drawContours(img1,counts,-1,(255,0,0),2)
cv.imshow("img1",img1)#凸包检测，获取凸包点
for count in counts: #for循环遍历所有轮廓点hull = cv.convexHull(count)# 绘制凸包binary1 = cv.polylines(img1, [hull], True, (0, 255, 0), 2)
cv.imshow("binary1",binary1)#显示效果
cv.waitKey(0)
cv.destroyAllWindows()