02324-离散数学-速记宝典

命题来源 围绕学科的基本概念、原理、特点、内容。

答题攻略

（1）不能像名词解释那样简单，也不能像论述题那样长篇大论，但需要加以简要扩展。

（2）答案内容要简明、概括、准确，即得分的关键内容一定要写清楚。

（3）答案表述要有层次性，列出要点，分点分条作答，不要写成一段；

（4）如果对于考题内容完全不知道，利用选择题找灵感，找到相近的内容，联系起来 进行作答。如果没有，随意发挥，不放弃。

考点 1 ：命题的基本概念。

（1）数理逻辑的任务是采用数学方法研究抽象的思维规律，研究的中心问题是推理，而推 理基本要素是命题。

（2）具有确切真值的陈述句称作命题。

（3）所谓真值就是命题为真或为假的性质。

（4）判断一个语句是否为命题，首先要判断它是否是陈述句，然后判断是否具有唯一的真 假值。

（5）在判断一个陈述句是否具有唯一的真假时，要注意：一个陈述句的真假暂时不能唯一 地确定，但总有一天可以唯一确定，与一个陈述句的真假不能唯一确定是两件事。

考点2：简述命题联结词有哪些。

（1）否定： ￢

（2）合取： ∧

（3）析取： ∨

（4）条件：P→Q

（5）双条件：P↔ Q

考点3：简述命题演算的合式公式规定。

（1）单个命题变元或命题常量（含 1 或 0）本身是一个合式公式

（2）如果 A 是合式公式，那么¬A 是合式公式

（3）如果 A 和 B 是合式公式，那么（A ∧ B）（AVB）、（A→B 和（A4→B）都是合式公式

（4）当且仅当有限次地应用（1）（2）（3）所得到的包含命题变元，联结词和圆括号的符号 串是合式公式。

合式公式亦称作命题公式或简称公式

考点4 ：指派与真值表。

（1）一个含有命题变元的命题公式是没有确定真值的。只有在命题公式中每个命题变元用 指定的命题常量代替后，命题公式才有确定的真值，成为命题。

（2）设 P 为一命题公式，P1 ，P2 ， … , Pn 为出现在 P 中的所有命题变元，对 P1 ，P2 ， … , Pn 指定一组真值称为对 P 的一种指派（解释或赋值）。若指定的一种指派，使 P 的值为真，则 称这组值为成真指派；使 P 的值为假，则称这组值为成假指派。

（3）含 n 个命题变元的命题公式，共有 2n 组指派。

（4）将命题公式 P 在所有指派下取值情况，列成表，称为 P 的真值表。 

考点5：简述真值表的构造方法。

（1）如果公式 A 中有 n 个命题符（命题变元），则 A 的真值表共有 2n+1行。第一行称为表 头，在表头的第一列写出所有的命题符，从表头第二列开始，依次写上公式 A 的生成过程中 生成的子串（这些子串也是子公式）。

（2）剩下的2n 行，每一行对应一个指派。一般按二进制的加法顺序依次赋值。

（3）对于每一个指派，依次求出各个子串的值，直到最后求出 A 的值。 

考点6：简述公式的分类。

（1）设 A 为一命题公式，若 A 在它的各种指派情况下，其取值均为真，则称公式 A 为重言 式或永真式。

（2）设 A 为一命题公式，若 A 在它的各种指派情况下，其取值均为假，则称公式 A 为矛盾 式或永假式。

（3）设 A 为一命题公式，若 A 在各种真值指派下至少存在一组成真指派，称 A 是可满足式。 若可满足式 A 至少存在一个成假赋值，则 A 称为非重言式的可满足式。

考点7：常用的等价式。

（1）双重否定律： ┐┐P == P

（2）结合律：（P∧Q） ∧R == P∧（Q∧R） （P∨Q） ∨R == P∨（Q∨R） （P↔ Q）↔ R == P↔ （Q↔ R）

（3）交换律： P∧Q == Q∧P

P∨Q == Q∨P

P↔ Q == Q↔ P

（4）分配律： P∧（Q∨R ） == （P∧Q） ∨（P∧R） P∨（Q∧R） == （P∨Q） ∧（P∨R）

（5）幂等律： P∨P == P P∧P == P

（6）吸收律： P∧（P∨Q）== P  P∨（P∧Q）==  P

（7）德.摩根律：┐（P∨Q）== ┐P∧┐Q  ┐（P∧Q）==  ┐P∨┐Q

（8）同一律： P∨F∧ P  P∧T == P

（9）零律： P∨T ==  T P∧F  == F

（10）否定律：P∨┐P  == T P∧┐P ==  F

（11）蕴涵等值式：P→Q  ==  ┐P∨Q

（12）等价等值式：P↔ Q  == （P→Q） ∧（Q→P）

（13）假言易位：P→Q  == ┐Q → ┐P

（14）等价否定等值式： P↔ Q  == ┐P↔ ┐Q

（15）归谬论：（P→Q ） ∧（ P→┐Q）  == ┐P

考点8：简述命题公式的分类。

设 A 为任一命题公式，

（1）若 A 在其各种赋值下的取值均为真，则称 A 是重言式或永真式，记为 T 或 1。

（2）若 A 在其各种赋值下的取值均为假，则称 A 是矛盾式或永假式，记为F 或0。

（3）若 A 不是矛盾式则称 A 为可满足式（satisfiable）。注：由定义可知，重言式一定是 可满足式，反之不真。

考点9：简述范式的定理。

（1）一个简单析取式是重言式当且仅当它同时含某个命题变项及它的否定式。

（2）一个简单合取式是矛盾式当且仅当它同时含有某个命题变项及它的否定式。

考点 10：简述析取范式与合取范式的性质。

（1）一个析取范式是矛盾式，当且仅当它的每一个简单合取式都是矛盾式；

（2）一个合取范式是重言式，当且仅当它的每一个简单析取式都是重言式。 

考点 11：简述求命题公式的范式的基本步骤。

（1）将公式中的联结词化归成┐ , ∧及∨。

（2）将否定联结词消去或内移到各命题变元之前。

（3）利用分配律、结合律将公式转化为合取范式或析取范式。

考点 12：简述利用真值表法求主析取范式、主合取范式。

（1）在真值表中，一个公式的真值为 T 的指派所对应的小项的析取，即为此公式主析取范 式。

（2）在真值表中，一个公式的真值为 F 的指派所对应的大项的合取，即为此公式主合取范 式。

考点 13：简述从 A 的主析取范式求其主合取范式步骤。

（1）求出 A 的主析取范式中未包含小项的下标。

（2）把（1）中求出的“下标”写成对应大项。

（3）做（2）中写成的大项合取，即为 A 的主合取范式。

考点 14：简述构造论证法常用的推理规则。

（1）前提引入规则：在证明的任何步骤上，都可以引入前提，简称 P 规则。

（2）结论引入规则：在证明的任何步骤上，所证明的结论都可作为后续证明的前提，称为 T 规则。

（3）置换规则：在证明的任何步骤上，命题公式中的任何子命题公式都可以用与之等值的 命题公式置换。亦记为 T 规则。

考点 15：简述量词的种类。

考点 16：简述谓词演算的合式公式。

谓词演算的合式公式，可由下述各条组成（合式公式 A 记为WffA）：

（1）原子谓词公式是合式公式。

（2）若 A 是合式公式，则￢A 是一个合式公式。

（3）若 A 和 B 都是合式公式，则（AVB（A∧B），（A→B），（A↔ B）是合式公式。

（5）只有经过有限次应用以上规则所得到的式是合式公式。

考点 17 ：在谓词合式公式中，有的个体变元既可以是约束出现，又可以是自由出现，为了 避免混淆采用两个改名规则。

（1）约束变元改名规则：将量词辖域中，某个约束出现的个体变元及相应指导变元改成本 辖域中未曾出现过的个体变元，其余不变。

（2） 自由变元代入规则：对某自由出现的个体变元可用个体常元或用在原子公式中和所有 个体变元不同的个体变元去代入，且处处代入。

考点 18：简述前束范式的转换步骤。

（1）先将蕴含或等价联结词转换；

（2）利用量词否定等值式，把否定深入到命题变元和谓词公式前面；

（3）换名或替换；

（4）利用量词辖域的收缩与扩张等值式，把量词提到前面。

考点 19：简述集合的表示法。

（1）列举法就是将集合的元素逐一列举出来的方式。例如，光学中的三原色可以用集合{红， 绿，蓝}表示；由四个字母 a,b，c,d 组成的集合 A 可用 A={a，b，c,d}表示，如此等等。

（2） 描述法的形式为{代表元素 ∣ 满足的性质}。 由 2 的平方根组成的集合 B 可表示为 B={x|x2=2}。

（3）图像法

（4）符号法

考点20：集合的基本运算。

（1）交集：由属于 A 且属于 B 的相同元素组成的集合，记作A∩B（或 B∩A），读作“A 交 B” （或“B 交 A”）

（2）并集：由所有属于集合 A 或属于集合 B 的元素所组成的集合，记作A∪B（或B∪A）， 读作“A 并 B”（或“B 并 A”）

（3）补集：补集又可分为相对补集（差集）和绝对补集

考点21：集合运算的恒等式。

（1）幂等律 A∪A=A， A∩A=A

（2）交换律 A∪B=B∪A， A∩B=B∩A

（3）结合律（A∪B） ∪C=A∪（B∪C） ；（A∩B） ∩C=A∩（B∩C）

（4）分配律 A∪（B∩C）=（A∪B） ∩（A∪C）； A∩（B∪C）=（A∩B） ∪（A∩C）

（5）德摩根律

绝对形式 ~（B∪C）=~B∩~C；  ~（B∩C）=  ~B∪~C

相对形式 A-（B∪C）=（A-B） ∩（A-C）；A-（B∩C）=（A-B） ∪（A-C）

（6）吸收律 A∪（A∩B）=A， A∩（A∪B）=A

（7）零律 A∪E=E， A∩Φ=Φ

（8）同一律 A∪Φ=A， A∩E=A

（9）排中律 A∪~A=E

（10）矛盾律 A∩~A=Φ

（11）余补律 ~ Φ=E， ~E=Φ

（12）双重否定律 ~~A=A

（13）补交转换律 A-B= A∩~B

考点22：集合 X 上二元关系 R 的性质。

（3）对称性

（4）反对称性

（5）传递性

考点23：关系矩阵的布尔运算。

（1）定义法：对于集合表示的关系 R，计算 Rn  就是 n 个 R 左复合。

（2）矩阵乘法：矩阵表示就是 n 个矩阵相乘，其中相加采用逻辑加。（线性代数，逻辑乘法）。

（3）关系图法：若点 a 经 k（k=1，2， … , n）条线可到达点 b，则在的关系图 Mk 上，a 到 b 有线相连。

考点 24：关系图法。

（1） 自反闭包图：对没有加环的点加环

（2） 对称闭包图：单边的加方向相反的边

（3） 传递闭包图：若 Ai 经过两条或两条以上的边可到达 Aj，且无边<Ai，Aj>则加边<Ai，Aj> 

考点25：相容关系和等价关系区别与联系。

（1）相容关系和覆盖：

① 是自反的、对称的

② 集合中的相容关系能构成该集合的覆盖

③ 相容关系不一定是等价关系

④ 覆盖不一定是划分

（2）等价关系和划分：

① 是自反的、对称的和传递的

② 集合中的等价关系能构成该集合的划分

③ 等价关系一定是相容关系

④ 划分一定是覆盖

考点 26：满射（映上）、单射（入射）、双射（一一对应）

（1）单射就是只能一对一，不能多对一。

（2）满射只要 Y 中的元素在 X 中都能找到原像就行了（一对一，多对一都行）。

（3）双射就是既是单射又是满射（一个对一个，每个都不漏掉）。

考点27：从 n 元代数运算的定义可知它有三点涵义。

（1）A 中任意 n 个元素都有运算结果；

（2）运算是封闭的，即运算结果仍在 A 中；

（3）结果是唯一的。

考点28：二元运算的性质。

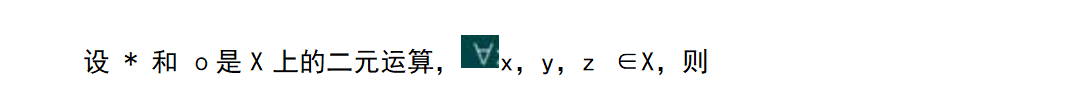
（1）封闭性：若 x，y ∈X，则 x*y∈X；

（2）可交换性：x*y=y*x；

（3）可结合性 ：x*y*z=x*（y*z）=（x*y）*z；

（4）可分配性：若 x*（y οz）=（x*y） ο（x*z）（y οz）*x=（y*x） ο（z*x）则称*对 ο 可分配。

（5）吸收律：设*和 ο是定义在集合 A 上的两个可交换的二元运算，若有 x*（x οy）=x，x ο（x*y）=x .则称*和 ο满足吸收律。

考点29：二元运算的一些重要性质。

（1）设“ ⊙”是非空集合 A 上的二元运算，如果对任意的 a、b、c∈A，有（a⊙b） ⊙c=a ⊙（b⊙c），则称运算“⊙”满足集合律。

（2）设“⊙”是非空集合 A 上的二元运算，如果对任意的 a，b∈A，有 a⊙b=b⊙a，则称运 算“⊙”满足交换律。

（3）设（A；*， ⊙) 是一代数系统，如果对任意的 a、b、c∈A，有 1）a*（b⊙c）=（a*b） ⊙（a*c），则称“*”对“ ⊙”有左分配律；2）（b⊙c）*a=（b*a） ⊙（c*a），则称“*”对 “⊙”有右分配律。

（4）封闭性、幂等律、吸收律等

考点30：由运算表判别算律的一般方法。

（1）交换律：运算表关于主对角线对称

（2）幂等律：主对角线元素排列与表头顺序一致

（3）单位元：所在的行与列的元素排列都与表头一致

（4）零元：元素的行与列都由该元素自身构成

（5）A 的可逆元：a 所在的行中某列（比如第 j 列）元素为e，且第 j 行 i 列的元素也是

e，那么a 与第 j 个元素互逆

（6）结合律：除了单位元、零元之外，要对所有 3 个元素的组合验证表示结合律的等式是 否成立

考点31：给定非空集合 G，*是 G 上一个二元运算，有五个条件。

（1）封闭性成立，即对任意 x，y ∈G，有 x*y∈G。

（2）结合律成立，即对任意 x，y，z∈G，有 x*（y*z）=（x*y）*z。

（3）单位元存在，即 G 中存在一个元素 e，对任意 x∈G，有 x*e=e*x=x

（4）逆元存在，即对任意 x∈G，存在 x-1∈G，满足 x*x-1=x-1*x=e

（5）交换律成立，即对任意 xy ∈G，有 x*y=y*x。

如果满足 1，则<G，*> 是代数系统；

如果满足 1、2，则<G，*>是半群；

如果满足 1、2、3，则<G，*>是独异点，也称含幺半群；

如果满足 1、2、3、4，则<G，*>是群；

如果满足 1、2、3、4、5，则<G，*>是阿贝尔群，也称交换群。

考点 32：环与域

（1）除环不一定是整环，因为除环不一定是交换的；

（2）整环不一定是除环，因为整环的非零元素不一定有逆元；

（3）域既是整环，也是除环；

（4）数的普通加法和乘法满足交换律，所以整数环、有理数环、实数环等均是可交换环， 也都有各自的幺元 1，所以也都是含幺环；

（5）偶数集及其上定义的普通加法和乘法构成的环是交换环，但没有幺元，所以它不是含 幺环。整数环、有理数环、实数环等均是无零因子环，所以也都是整环。

（6）由于矩阵乘法不满足交换律，故 n 阶实矩阵环不是可交换环，单位矩阵是它的乘法幺 元。

（7）集合 A 的幂集关于集合的对称差运算和交运算构成的环是含幺元交换环。

（8）有理数环 Q 和实数环 R 都是域。

（9）但整数环 Z 不是域。

考点33：从分配格判定定理可以直接推得两个结论。

（1）每一条链都是分配格；

（2）小于五个元素的格都是分配格。

考点34：图 G 的结点与边之间的关系

（1）邻接点：同一条边的两个端点。

（2）孤立点：没有边与之关联的结点。

（3）邻接边：关联同一个结点的两条边。

（4）孤立边：不与任何边相邻接的边。

（5） 自回路（环）：关联同一个结点的一条边（（v，v）或〈v，v〉）。

（6）平行边（多重边）： 关联同一对结点的多条边。

考点35：按 G 的边有序、无序，图可分为哪几类。

（1）有向图：每条边都是有向边的图称为有向图；

（2）无向图：每条边都是无向边的图称为无向图；

（3）混合图：既有无向边，又有有向边的图称为混合图。

考点36：握手定理

（1）定理 1 在图 G=<V，E>中，顶点度数之和等于边数的两倍。

（2）定理2 任意的图 G，如果有奇顶点，则奇顶点的个数必为偶数个。

（3）定理3 在有向图中，所有点的入度之和等于所有顶点的出度之和。 

考点37：两个图同构的必要条件。

（1）结点数相等。

（2）边数相等。

（3）度数相同的结点数目相等

这三个条件只要有一个不成立，则两个图不是同构。但是如果这三个条件均满足也不能 说明两个图是同构的。当前还没有一种简单有效的方法来判断两图的同构，要证明图的同构 只能分别写出结点和边的对应关系。

考点38：有向图的连通性。

设有有向图 G，

（1）若 G 的任意两个结点中，至少从一个结点可达另一个结点，则称图 G 是单向连通的；

（2）如果 G 的任意两个结点都是相互可达的，则称图 G 是强连通的；

（3）如果略去边的方向后，G 成为连通的无向图，则称图 G 是弱连通的。 考点39：树的基本概念.

（1）无回路的连通无向图称为树。

（2）树没有回路，所以树中不含多重边或环，任何树都是简单图。

（3）孤立结点也是树，称其为平凡树。

（4）树中度数为 1 的结点称为树叶结点，度数大于 1 的结点称分支点。

（5）一个无回路的无向图 G，若它的每个连通分图是树，则图G 称作森林。 考点40：无向图 T 是树，当且仅当以下六条之一成立。

（1）T 无回路且连通。

（2）T 无回路且 m＝n－1，其中 m 是边数，n 是结点数。

（3）T 连通且 m＝n－1。

（4）T 无回路，但增加一条新边，得到—个且仅一个初级回路。

（5）T 连通，但删去任一边后便不连通。

（6）T 的每一对结点间有且仅有一条初级路。