当前位置：首页 > news >正文

二叉树的概念以及二叉树的分类，添加，删除

news 2025/11/11 20:03:57

一、二叉树基本概念

（一）引言：树是一种非线性的数据结构，数据逻辑中之所以会引入“树”这个东西，是借助了生活中树的“分支”的概念。逻辑数据中的树可用于描述一种类似组织结构的关系。在一堆数据中包含一个称为”根”的节点，其他的节点再次组成一个新的“树”，树的定义是一种递归的定义。数据逻辑上的树一般习惯“倒着”，即：根在上，分支和叶子在下。

（二）概念：二叉树是重要的非线性数据结构。

（三）相关术语：

结点：树中元素及其子树

孩子/双亲：一个结点的后继结点叫做该结点的孩子，该结点叫做汉字的双亲结点。

结点的度：该结点分支的数量。

叶子：该结点分支数量为零。

结构的层次：从根到该节点的层数（根的层次为一）；

树的高度（深度）：树中结点层次的最大值。

1.满二叉树：

一棵深度为k,且有2^k-1个结点的二叉树，称为满二叉树。这种树的特点是每一层上的特点都是最大最大节点数。

2.完全二叉树：

在一颗二叉树中，除了最后一层外，若其余层都是满的，或者最后一层外，或者是最后一层在右边缺少连续若干结点，则此二叉树是完全二叉树。

二叉排序树（Binary Sort Tree)又被称为二叉查找（搜索)树（Binary Search Tree)。其定义为：二叉排序树或者是空树，或者满足以下性质的二叉树：

若它的左子树非空，则左子树上所有结点的值均小于根结点的值；

若它的右子树非空，则右子树上所有节点的值均大于根结点的值；

左、右子树本身又各是一棵二叉树。

二叉树的创建：

//将int类型重定义为DATA类型

//令NULL代表0，用它来表示“空地址”

//令LEN代表struct node类型数据的长度

建立链表的函数如下：

#include <stdio.h>
typedef int DATA; //将int类型重定义为DATA类型
#define NULL 0    //令NULL代表0，用它表示“空地址”
#define LEN sizeof(struct node)  //令LEN代表struct node类型的数据的长度struct node{DATA data;struct node*left;struct node*right;};

后续代码：

struct node*Create(DATA dt)
{struct node*root;root=(struct node*)malloc(LEN);root->data=dt;root->left=NULL;root->right=NULL;return root;
}

二叉树的插入过程：

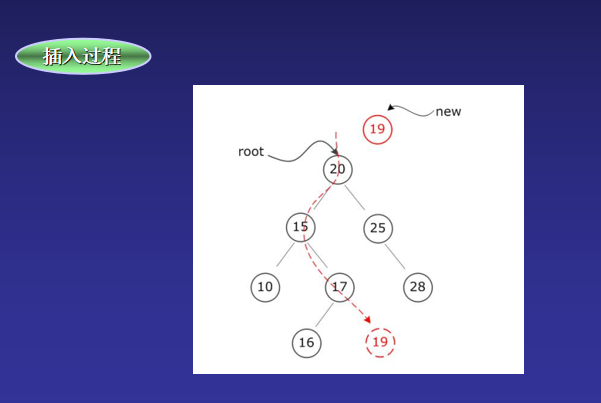
口诀：

前序遍历：根左右

中序遍历：左根右

后序遍历：左右根

前序遍历：从根结点出发，则第一次到达结点A，故输出A；继续向左访问，第一次访问结点B，故输出B；按照同样的规则，输出D，输出H；

当到达叶子结点H，返回到D，此时已经是第二次到达D，故不输出D，进而向D右子树访问，D右子树不为空，则访问至I，第一次到达I，则输出I；

I为叶子结点，则返回到D，D左右子树已经访问完毕，则返回到B，进而到B子树，第一次到达E，故输出E；向E左子树，故输出J；

按照同样的访问规则，继续输出C、F、G

前序遍历输出结果为：ABDHIEJCFG

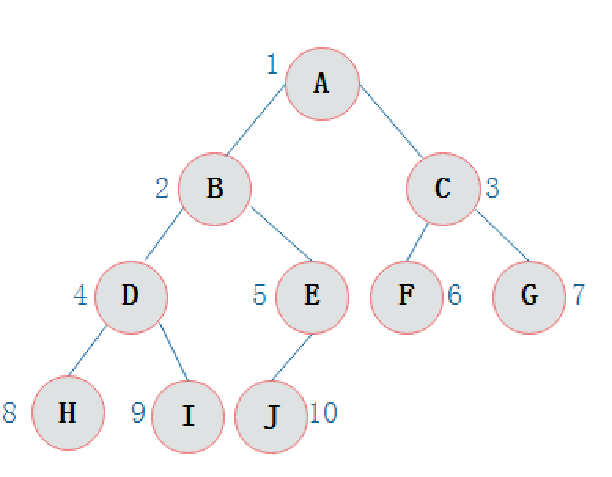
前序遍历通俗一点来说就是从二叉树的根结点出发，先输出根结点数据，然后输出左结点，最后输出右节点的数据。

中序遍历：从根结点出发，则第一次到达结点A，不输出A，继续向左访问，第一次访问结点B，BU不输出B；继续到达D、H；

到达H,H左子树为空，则返回到H，此时第二次访问H，故输出H;

H右子树为空，则返回至D，此时第二次到达D，故输出D；

由D返回至B，第二次到达B，故输出B；按照同样规则继续访问，输出J、E、A、F、C、G;

中序遍历通俗来说就是从二叉树的根结点出发，先输出左节点数据，然后输出根结点，最后输出右结点的数据。

中序遍历输出结果为：H、D、I、B、J、E、A、F、C、G

后序遍历：从根结点出发，则第一次到达结点A，不输出A，继续向左访问，第一次访问结点B，不输出B；继续到达D，H；到达H，H左子树为空，则返回到H，此时第二次访问H，不输出H； H右子树为空，则返回至H，此时第三次到达H，故输出H；由H返回至D，第二次到达D，不输出D；继续访问至I，I左右子树均为空，故第三次访问I时，输出I；返回至D，此时第三次到达D，故输出D；按照同样规则继续访问，输出J、E、B、F、G、C，A；

后序遍历通俗的说就是从二叉树的根结点出发，先输出左结点数据，然后输出右结点，最后输出根结点的数据。

后序遍历输出为： HIDJEBFGCA。

二叉树的结点删除

先找到要删除的结点，然后判断待删除的结点的子树情况。

如果待删除的结点只有左子树，那么就将其左子树中的最大的结点替换掉该结点。

如果待删除的结点只有右子树，那么就将其右子树中的最小的结点替换掉该结点。

待删除的结点就是一个叶子结点，直接删除。

二叉树的查找：

从根结点出发

如果比根结点小，那么就去其左子树找。

如果比根结点大就去其右子树找

找到叶子都没找到，就代表查找失败。