当前位置：首页 > news >正文

特征降维实战：高效选择关键特征

news 2025/11/11 20:53:47

特征工程-特征降维

特征降维

实际数据中，特征过多会增加计算量、引入噪声、降低模型泛化能力。降维的目标是：

减少维度，同时尽可能保留重要信息。

降维的好处：

降低计算成本：减少训练时间与资源消耗。
去除噪声：移除冗余或无关特征，缓解过拟合。

降维方法分为两类：

特征选择：直接挑选最有用的原始特征。
特征提取：将原特征通过变换生成新的低维特征（如 PCA）。

1. 特征选择

(a) 低方差过滤（VarianceThreshold）

核心思想：方差小的特征变化不大，区分度低，可删除。

计算方差：
$\sigma^2 = \frac{1}{n} \sum_{i=1}^n (x_i - \bar{x})^2$
设定阈值：方差低于阈值的特征视为无用。
过滤特征：移除低方差特征。

代码示例：

from sklearn.feature_selection import VarianceThreshold
import numpy as np
np.random.seed(42)
data = np.random.randint(0,10,(5,3))
print(data)
transfer = VarianceThreshold(threshold=2)
data_new = transfer.fit_transform(data)
print(data_new)
transfer.variances_ # 获取每个特征方差

输出结果：

[[6 3 7][4 6 9][2 6 7][4 3 7][7 2 5]][[6 3][4 6][2 6][4 3][7 2]]array([3.04, 2.8 , 1.6 ])

从结果可以看出，特征从我们的三维到二维，保留原始的特征，只是将方差小的特征进行去除。

0f6a26956923bf7f3c6a4243af23cef4_720

(b) 皮尔逊相关系数（Pearson Correlation）

皮尔逊相关系数（Pearson correlation coefficient)是一种度量两个变量之间线性相关性的统计量。它提供了两个变量间关系的方向（正相关或负相关）和强度的信息。皮尔逊相关系数的取值范围是 [−1,1]，其中：

$r = 1$ 表示完全正相关，即随着一个变量的增加，另一个变量也线性增加。
$r = - 1$ 表示完全负相关，即随着一个变量的增加，另一个变量线性减少。
$r = 0$ 表示两个变量之间不存在线性关系。

正相关、负相关、不相关：

正相关：一个变量增加，另一个也增加；
负相关：一个变量增加，另一个减少；
不相关：变量变化无显著线性关系。

皮尔逊相关系数公式：
$\frac{\sum_{i=1}^n (x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\sum_{i=1}^n (x_i - \bar{x})^2} \sqrt{\sum_{i=1}^n (y_i - \bar{y})^2}}$

$\approx 1$ ：强相关；
$\approx 0$ ：弱相关。
$∣ r ∣ < 0.4$ 为低度相关; $ 0.4<=|r|<0.7$为显著相关； $0.7 <= ∣ r ∣ < 1$ 为高度相关

scipy.stats.personr(x, y) 计算两特征之间的相关性

返回对象有两个属性:

statistic皮尔逊相关系数[-1,1]

pvalue零假设(了解),统计上评估两个变量之间的相关性,越小越相关

代码示例：

import numpy as np
import pandas as pd
from sklearn.datasets import load_breast_cancer
from scipy.stats import pearsonrdata = load_breast_cancer()
X = pd.DataFrame(data.data,columns=data.feature_names)
y = data.target
# X.head()correlations = [] # 保存相关系数
p_values = [] # 保存p值for col in X.columns:corr, p = pearsonr(X[col], y)  # 计算相关系数和p值correlations.append(corr)p_values.append(p)corr_df = pd.DataFrame({"feature_names": X.columns,  # 特征名称"correlations": correlations,  # 相关系数"p_values": p_values,  # p值}
)corr_df

	feature_names	correlations	p_values
0	mean radius	-0.730029	8.465941e-96
1	mean texture	-0.415185	4.058636e-25
2	mean perimeter	-0.742636	8.436251e-101
3	mean area	-0.708984	4.734564e-88
4	mean smoothness	-0.358560	1.051850e-18
5	mean compactness	-0.596534	3.938263e-56
6	mean concavity	-0.696360	9.966556e-84
7	mean concave points	-0.776614	7.101150e-116
8	mean symmetry	-0.330499	5.733384e-16
9	mean fractal dimension	0.012838	7.599368e-01
10	radius error	-0.567134	9.738949e-50
11	texture error	0.008303	8.433320e-01
12	perimeter error	-0.556141	1.651905e-47
13	area error	-0.548236	5.895521e-46
14	smoothness error	0.067016	1.102966e-01
15	compactness error	-0.292999	9.975995e-13
16	concavity error	-0.253730	8.260176e-10
17	concave points error	-0.408042	3.072309e-24
18	symmetry error	0.006522	8.766418e-01
19	fractal dimension error	-0.077972	6.307355e-02
20	worst radius	-0.776454	8.482292e-116
21	worst texture	-0.456903	1.078057e-30
22	worst perimeter	-0.782914	5.771397e-119
23	worst area	-0.733825	2.828848e-97
24	worst smoothness	-0.421465	6.575144e-26
25	worst compactness	-0.590998	7.069816e-55
26	worst concavity	-0.659610	2.464664e-72
27	worst concave points	-0.793566	1.969100e-124
28	worst symmetry	-0.416294	2.951121e-25
29	worst fractal dimension	-0.323872	2.316432e-15

2. 主成分分析（PCA）

核心思想：找到方差最大的投影方向，用较少的新特征表示大部分信息。

PCA的核心目标是从原始特征空间中找到一个新的坐标系统，使得数据在新坐标轴上的投影能够最大程度地保留数据的方差，同时减少数据的维度。

(a) 原理

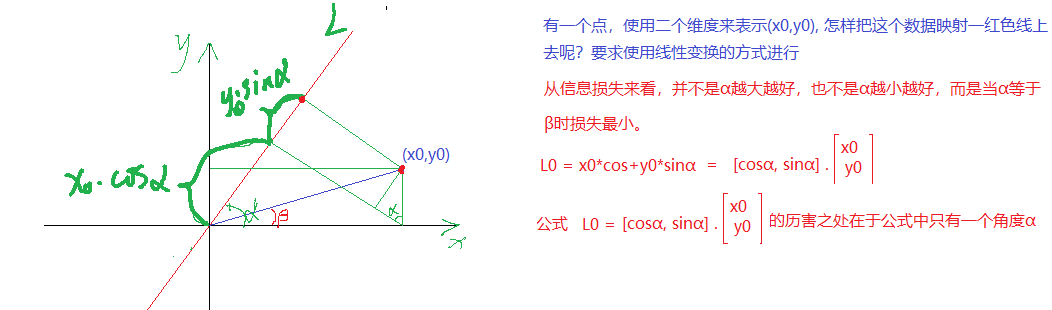
$x_0$ 投影到 $L$ 的大小为 $x0∗cosαx_0*cos \alpha$

$y_0$ 投影到 $L$ 的大小为 $y0∗sinαy_0*sin\alpha$

使用 $x_0,y_0)$ 表示一个点，表明该点有两个特征，而映射到L上有一个特征就可以表示这个点了。这就达到了降维的功能。

投影到L上的值就是降维后保留的信息，投影到与L垂直的轴上的值就是丢失的信息。保留信息/原始信息=信息保留的比例

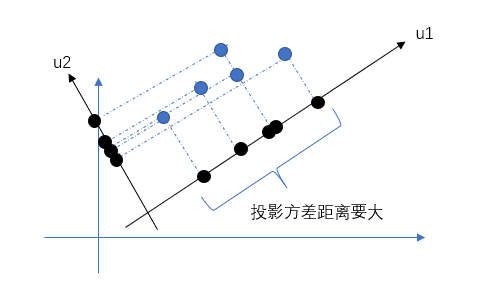
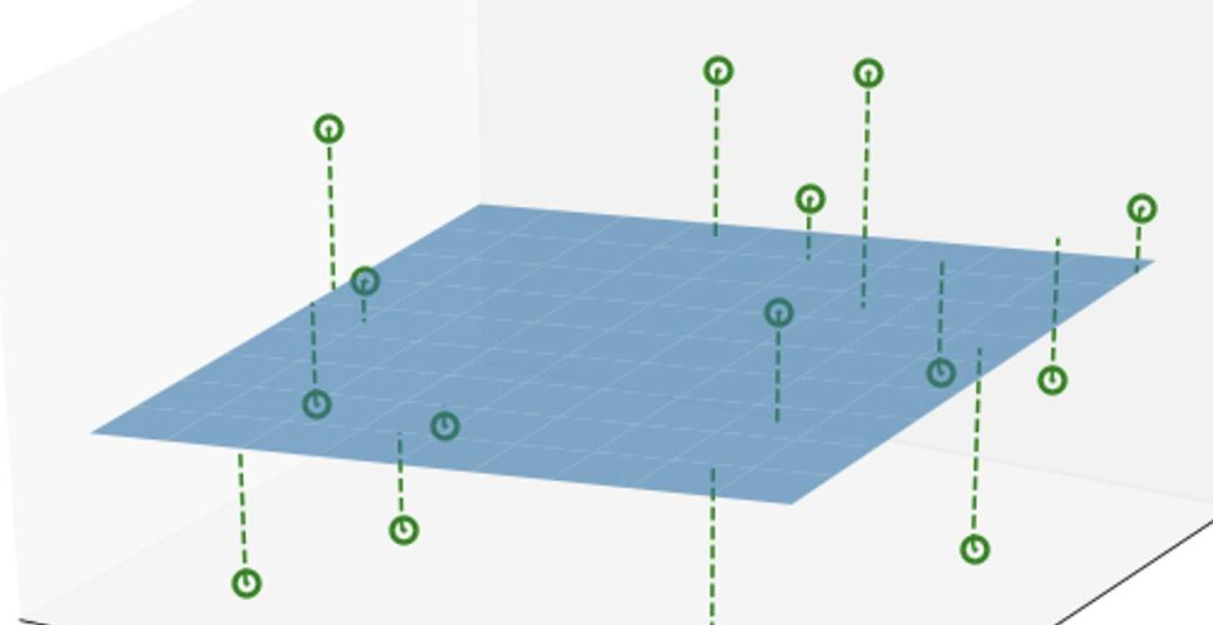
(a) 几何解释

将二维点投影到一条直线上；
保留投影（信息最大化），舍弃垂直方向（信息最小化）。

(b) 数学步骤

数据中心化；
计算协方差矩阵；
求解特征值与特征向量；
选取前 $k$ 个主成分；
投影：

$Z = X W_k$

© 代码示例

import numpy as np
import pandas as pd
from sklearn.datasets import load_breast_cancer
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
from matplotlib.patches import Patch
data = load_breast_cancer()
X = data.data
y = data.target
feature_names = data.feature_names
feature_names
# 标准化
scaler = StandardScaler()
X_std = scaler.fit_transform(X)
# PCA 降维保留2维
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X_std)
X_pca
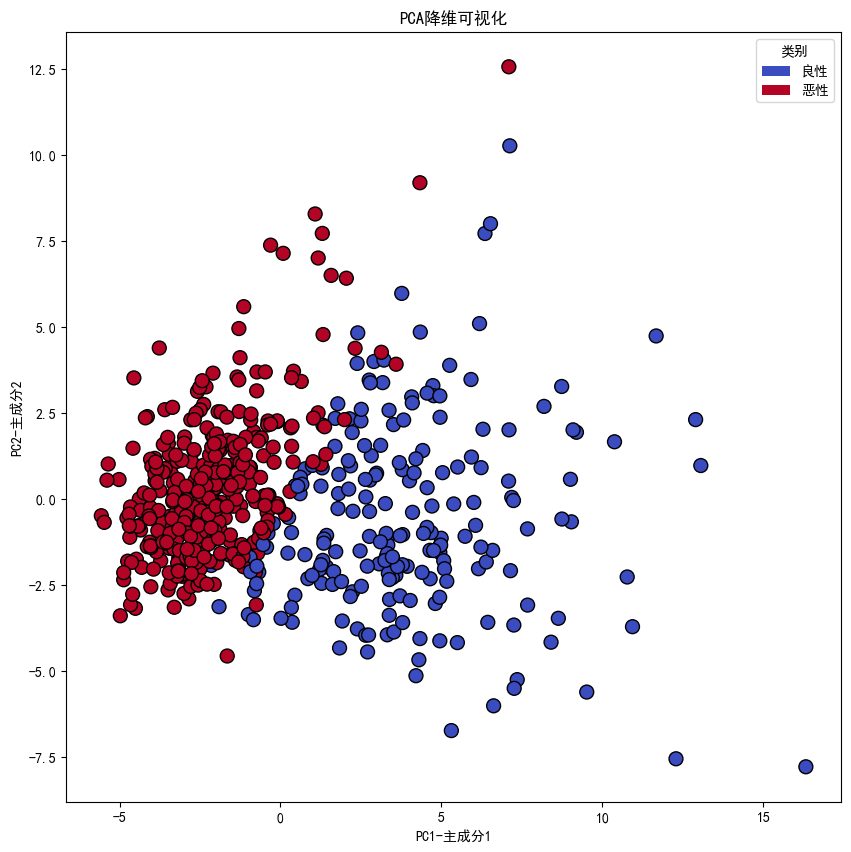
# 可视化PCA结果
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = Falseplt.figure(figsize=(10, 10))
plt.scatter(X_pca[:,0],X_pca[:,1],c=y,cmap='coolwarm',edgecolor='k',s=100)
plt.xlabel('PC1-主成分1')
plt.ylabel('PC2-主成分2')
plt.title('PCA降维可视化')class_labels = {0:'良性',1:'恶性'}
# 设置颜色映射
colors = plt.cm.coolwarm(np.linspace(0,1,len(class_labels)))
# 创建图例
legend_elements = [Patch(facecolor=colors[i],label=class_labels[i]) for i in class_labels.keys()]
plt.legend(handles=legend_elements,title='类别')
plt.show()

总结提炼

降维方法对比

方法	思路	是否保留原始特征	适用场景
低方差过滤	删除变化小的特征	是	初步清洗
皮尔逊相关系数	选择与目标或特征不冗余的特征	是	可解释性强
PCA	通过投影生成新特征	否	高维连续特征

实践建议

先用特征选择清理冗余；
再用 PCA 压缩高维特征；
注重可解释性时用特征选择，注重信息保留时用 PCA

好的，可以把 PCA 和 矩阵左乘 结合起来总结矩阵乘法的几何意义。

1. PCA 本质是矩阵左乘

假设原始数据矩阵是：
$\in \mathbb{R}^{n \times d}$

$n$ ：样本数量
$d$ ：特征数量

PCA 通过线性变换把 dd-维特征降到 kk-维：
$Z = X W_k$
其中：

$Wk∈Rd×kW_k \in \mathbb{R}^{d \times k}$ ：投影矩阵，由协方差矩阵的前 kk 个特征向量组成；
$\in \mathbb{R}^{n \times k}$ ：降维后的表示。

所以 PCA 实际上就是把原始矩阵 $X$ 左乘 一个投影矩阵 $W_k$ ，将原特征映射到新的坐标系。

2. 矩阵左乘的几何意义

旋转（改变坐标系）：如果 $W_k$ 是正交矩阵（特征向量正交化），左乘相当于把数据旋转到“主成分方向”；
投影（降维）：只取前 $k$ 个主成分，相当于把高维点投影到一个低维超平面；
缩放（方差大小）：如果再乘以特征值的平方根，会体现不同主成分的方差大小。

直观示例

二维数据 $X$ ：
$\begin{bmatrix} x_1 & y_1 \\ x_2 & y_2 \\ x_3 & y_3 \end{bmatrix}$
PCA 找到两个主成分 $w_1$ , $w_2$ ，组成投影矩阵：
$\begin{bmatrix} w_{11} & w_{12} \\ w_{21} & w_{22} \end{bmatrix}$
降维到一维时只取第一列 $w_1$ ：
$w_1 = \begin{bmatrix} x_1 & y_1 \\ x_2 & y_2 \\ x_3 & y_3 \end{bmatrix} \begin{bmatrix} w_{11} \\ w_{21} \end{bmatrix} = \begin{bmatrix} x_1 w_{11} + y_1 w_{21} \\ x_2 w_{11} + y_2 w_{21} \\ x_3 w_{11} + y_3 w_{21} \end{bmatrix}$