当前位置：首页 > news >正文

控制建模matlab练习10：滞后补偿器

news 2025/8/4 15:35:55

此练习主要是：关于滞后补偿器。
①滞后补偿器作用；
②不同滞后补偿器的效果；

一、为什么使用滞后补偿器

滞后补偿器：主要用于改善系统的稳态误差；
滞后补偿器设计思路：同时为系统增加一个极点和零点，与超前补偿器不同的是，滞后补偿器的极点的位置比零点更加靠近虚轴；
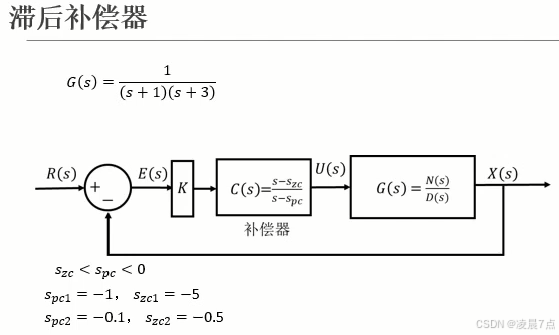
选取两组不同滞后补偿器，如图所示；
因为，两组滞后补偿器，零点极点的比值是一致的，所以改善稳态误差的效果是一致的；但是，由于位置很不同，所以对系统的瞬态响应有很大影响。
在matlab中，绘制对应的根轨迹，以及闭环系统的单位阶跃响应。
代码如下：

clc;clear;close all;
%% 定义G(s)
s = tf('s');
G_s = 1/((s+1)*(s+3));
K = 2;
t = 0:0.1:20;
%% 绘制原传递函数根轨迹及其响应
subplot(3,2,1);
rlocus(G_s);
title('原系统根轨迹');
subplot(3,2,2);
sys_1 = feedback(K*G_s, 1);
step (sys_1,t);
title('原系统单位阶跃响应');%%%% 定义补偿器C1(s)
sz = -5;
sp = -1;
C1_s = (s-sz)/(s-sp);
%% 使用补偿器C1(s)后的根轨迹及其响应
subplot(3,2,3);
rlocus(G_s*C1_s);
title('增加滞后补偿器C1系统根轨迹');
subplot(3,2,4);
sys_2 = feedback(K*G_s*C1_s, 1);
step (sys_2,t);  
title('增加滞后补偿器C1系统单位阶跃响应');%%%% 定义补偿器C2(s)
sz = -0.5;
sp = -0.1;
C2_s = (s-sz)/(s-sp);
%% 使用补偿器C1(s)后的根轨迹及其响应
subplot(3,2,5);
rlocus(G_s*C2_s);
title('增加滞后补偿器C2系统根轨迹');
subplot(3,2,6);
sys_3 = feedback(K*G_s*C2_s, 1);
step (sys_3,t);  
title('增加滞后补偿器C2系统单位阶跃响应');

二、运行结果及分析

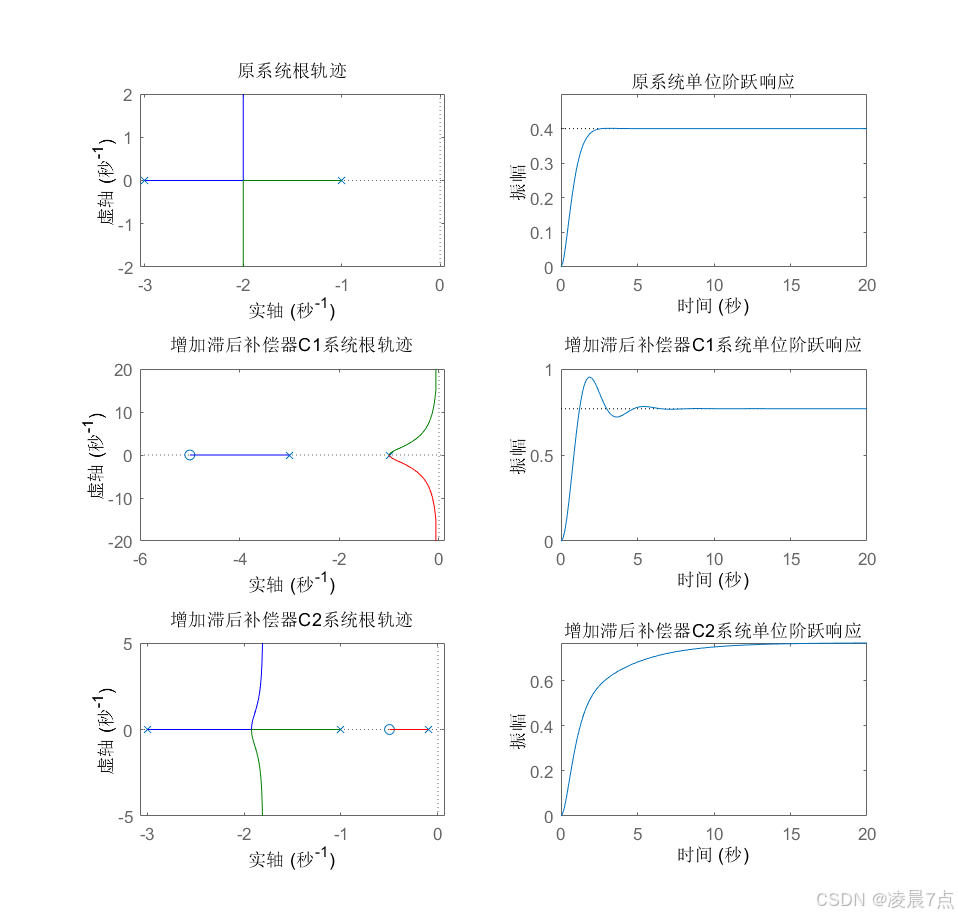
1、从原系统图：

原系统单位阶跃响应，最终将系统稳定在0.4左右，所以稳态误差是1-0.4=0.6；

2、增加补偿器C1系统图：sz=-5；sp=-1；

增加C1补偿器系统单位阶跃响应，最终将系统稳定在0.8左右，所以稳态误差是1-0.8=0.2；
当增加C1：sz=-5；sp=-1；此时完全改变了原因系统的根轨迹方向，因此，此时的单位阶跃响应就会与原系统很不同；

3、增加补偿器C2系统图：sz=-0.5；sp=-0.1；

增加C2补偿器系统单位阶跃响应，最终将系统稳定在0.8左右，所以稳态误差是1-0.8=0.2；
当增加C2：sz=-0.5；sp=-0.1；此时只是增加了一条由x=-0.1指向x=-0.5的根轨迹，对原来根轨迹影响比较小，当前根轨迹还很一致，只是增加一条距离虚轴很近的根轨迹，因此，此时的单位阶跃响应就会与原系统比较类似；

4、总体来看

发现，增加C1和C2滞后补偿器，最后的曲线截然不同。
当增加C1滞后补偿器，就完全不同了，sz=-5；sp=-1；这对零极点就完全改变原有根轨迹的形态了，所以响应也就完全不同。
当增加C2滞后补偿器，可以看出，从0上升到0.4的过程，几乎和原系统一致，只是从0.4之后，再通过sz=-0.5；sp=-0.1；这对零极点来修正稳态误差。

滞后补偿器的运行结果