【算法笔记 day four】二分查找

(,,･∀･)ﾉ゛hello，大家好。从本次文章就开始更新二分算法的内容了，本篇的内容不多，也是比较基础的算法部分，大家可以好好消化一下。

1、基础二分

这块讲解灵神在B站上有视频，三个写法全闭、半开半闭，全开，建议大家看下面内容之前先去看看视频，会有很大的启发。（点我跳转）

例题1 — 34.在排序数组中查找元素的第一个和最后一个位置

给你一个按照非递减顺序排列的整数数组 nums，和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。

如果数组中不存在目标值 target，返回 [-1, -1]。

你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。

示例 1：

输入：nums = [5,7,7,8,8,10], target = 8
输出：[3,4]

示例 2：

输入：nums = [5,7,7,8,8,10], target = 6
输出：[-1,-1]

示例 3：

输入：nums = [], target = 0
输出：[-1,-1]

提示：

• 0 <= nums.length <= 105
• -109 <= nums[i] <= 109
• nums 是一个非递减数组
• -109 <= target <= 109

def binary_search(nums, target):left = -1right = len(nums)while left + 1 < right:mid = (left + right) // 2if nums[mid] < target:left = midelse:right = midreturn right
# 我个人比较喜欢开区间的写法，因为left可以直接=mid，比较简洁
# 这样调用：
# result = binary_search([1, 2, 3], 2)
class Solution:def searchRange(self, nums: List[int], target: int) -> List[int]:start = binary_search(nums, target)if start == len(nums) or nums[start] != target:return [-1, -1]return[start, binary_search(nums, target + 1) - 1]

#思路

具体思路视频里面已经很详细了，这里默认大家都看过了。没看懂的多看几遍，画画图肯定能过。如果看了n边还是不懂那可能要去请教一下你的老师同学们了。

这里主要是说一下我觉得可能会有疑惑的地方。首先，这个binary函数返回的是第一个大于等于target的位置；由于这个函数是写在类的外面，所以不需要加self（这个self是代表类本身的意思，大家不用想的很复杂）；最后一行代码要减一是因为返回的是闭区间，binary（target + 1）返回的是第一个大于等于target + 1的数的位置，那往他左边过去第一位不就是等于target的最后一个位置吗（题目说了数组是整数，所以可以这样用）；在其他语言要注意溢出这个问题，可以写成left + (right - left) / 2。因为left + right可能会大于本题的数据范围，但是在Python中没有溢出这个概念。

例题2 — 704.二分查找

给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target  ，写一个函数搜索 nums 中的 target，如果 target 存在返回下标，否则返回 -1。

你必须编写一个具有 O(log n) 时间复杂度的算法。
示例 1:

输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4

示例 2:

输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1

提示：

1. 你可以假设 nums 中的所有元素是不重复的。
2. n 将在 [1, 10000]之间。
3. nums 的每个元素都将在 [-9999, 9999]之间。

class Solution:def search(self, nums: List[int], target: int) -> int:left, right = -1, len(nums)while left + 1 < right:mid = left + (right - left) // 2if nums[mid] < target:left = midelse:right = midif  right < 0 or right > len(nums) - 1 :return -1if nums[right] != target:return -1return right

#思路

这题还是标准的二分查找的题目，思路和上一题一模一样，没什么好说的。拿来练手增加熟练度的。需要在意的地方还是mid，我们现在在写Python所以不用显式考虑整数溢出问题，因为 Python 的整数类型（int）具有任意精度。这意味着 Python 的整数可以表示任意大小的整数值，只要你的计算机内存允许。它们不是固定大小的（例如 32 位或 64 位），而是根据需要动态地分配内存来存储更大的数字。这个过程对开发者是透明的。但是在其他语言比如c或者c++、java里面就要考虑了，所以养成好习惯是很重要的。

另外这题的条件判断也有点意思，我选择的是过滤写法（return之后这个函数就停止了），最上层需要先去掉list index out of range这种情况，当然可以用

return right if right < len(nums) and nums[right] == target else -1

这个写法也是一样的。

例题3 — 744.寻找比目标字母大的最小字母

给你一个字符数组 letters，该数组按非递减顺序排序，以及一个字符 target。letters 里至少有两个不同的字符。

返回 letters 中大于 target 的最小的字符。如果不存在这样的字符，则返回 letters 的第一个字符。

示例 1：

输入: letters = ["c", "f", "j"]，target = "a"
输出: "c"
解释：letters 中字典上比 'a' 大的最小字符是 'c'。

示例 2:

输入: letters = ["c","f","j"], target = "c"
输出: "f"
解释：letters 中字典顺序上大于 'c' 的最小字符是 'f'。

示例 3:

输入: letters = ["x","x","y","y"], target = "z"
输出: "x"
解释：letters 中没有一个字符在字典上大于 'z'，所以我们返回 letters[0]。

提示：

• 2 <= letters.length <= 104
• letters[i] 是一个小写字母
• letters 按非递减顺序排序
• letters 最少包含两个不同的字母
• target 是一个小写字母

class Solution:def nextGreatestLetter(self, letters: List[str], target: str) -> str:left, right = -1, len(letters)while left + 1 < right:mid = left + (right - left) // 2if letters[mid] <= target  :left = midelse:right = midreturn letters[right] if right <= len(letters) - 1 else letters[0]

#思路

这题也是一道经典的二分查找，只是要稍微变化一下条件。我们原版代码里面查找的是第一个大于或者等于target的位置，现在这个题目要的是第一个大于target的位置，那其实就把等于这个条件去掉就好了，换而言之就是在等于时，right不动（因为right是要return的值，是最终的答案）。关键就在这里，没看懂的同学可以按照给的样例自己画图想想。还有一点要注意的就是如果没有这个大于的值，那就是说所有的值都小于等于target，那么最后这个right应该是len（letters），就是相当于没动。

2、进阶二分

部分题目需要先排序，然后在有序数组上二分查找。还有些题目需要先数学变换再进行下一步操作。

例题4 — 2300.咒语和药水的成功对数

给你两个正整数数组 spells 和 potions ，长度分别为 n 和 m ，其中 spells[i] 表示第 i 个咒语的能量强度，potions[j] 表示第 j 瓶药水的能量强度。

同时给你一个整数 success 。一个咒语和药水的能量强度 相乘 如果 大于等于 success ，那么它们视为一对 成功 的组合。

请你返回一个长度为 n 的整数数组 pairs，其中 pairs[i] 是能跟第 i 个咒语成功组合的 药水 数目。

示例 1：

输入：spells = [5,1,3], potions = [1,2,3,4,5], success = 7
输出：[4,0,3]
解释：
- 第 0 个咒语：5 * [1,2,3,4,5] = [5,10,15,20,25] 。总共 4 个成功组合。
- 第 1 个咒语：1 * [1,2,3,4,5] = [1,2,3,4,5] 。总共 0 个成功组合。
- 第 2 个咒语：3 * [1,2,3,4,5] = [3,6,9,12,15] 。总共 3 个成功组合。
所以返回 [4,0,3] 。

示例 2：

输入：spells = [3,1,2], potions = [8,5,8], success = 16
输出：[2,0,2]
解释：
- 第 0 个咒语：3 * [8,5,8] = [24,15,24] 。总共 2 个成功组合。
- 第 1 个咒语：1 * [8,5,8] = [8,5,8] 。总共 0 个成功组合。
- 第 2 个咒语：2 * [8,5,8] = [16,10,16] 。总共 2 个成功组合。
所以返回 [2,0,2] 。

提示：

• n == spells.length
• m == potions.length
• 1 <= n, m <= 105
• 1 <= spells[i], potions[i] <= 105
• 1 <= success <= 1010

class Solution:def successfulPairs(self, spells: List[int], potions: List[int], success: int) -> List[int]:potions.sort()m = len(potions)success -= 1return [m - bisect_right(potions, success // x) for x in spells]

#思路

我这里选用的是灵神的思路，并且对其可能会产生困惑的地方进行相应的讲解。首先灵神使用的是库函数bisect，给大家简单介绍一下这个函数，left就是target值左边第一个值的索引个，最靠近target值的左边的那个数；left则是最靠近target值的右边的那个数。下图是详细说明

由于库函数是需要严格大于或者小于这种条件才可以使用的，所以我们必须要对原有条件进行调整。原题条件如下

我们需要把这个等于号去掉，可以这样变形

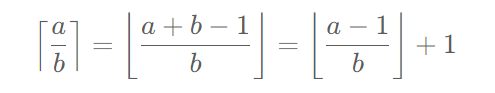
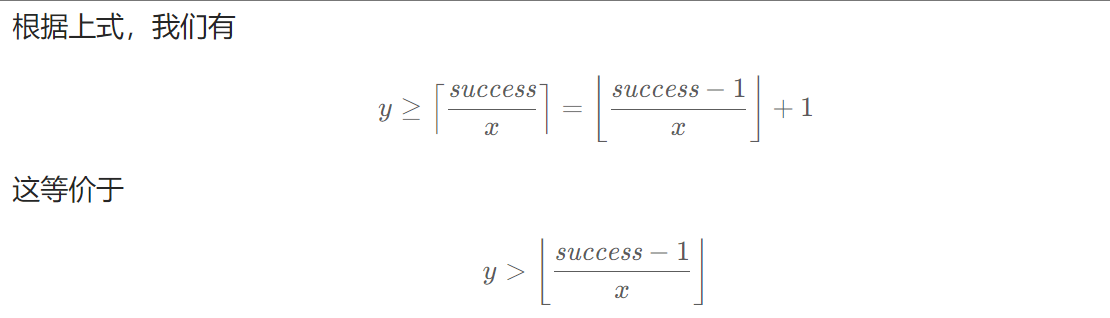
接下来就是常规操作了，不再重复赘述。

例题5 — 1385.两个数组间的距离值

给你两个整数数组 arr1 ， arr2 和一个整数 d ，请你返回两个数组之间的 距离值 。

「距离值」 定义为符合此距离要求的元素数目：对于元素 arr1[i] ，不存在任何元素 arr2[j] 满足 |arr1[i]-arr2[j]| <= d 。

示例 1：

输入：arr1 = [4,5,8], arr2 = [10,9,1,8], d = 2
输出：2
解释：
对于 arr1[0]=4 我们有：
|4-10|=6 > d=2 
|4-9|=5 > d=2 
|4-1|=3 > d=2 
|4-8|=4 > d=2 
所以 arr1[0]=4 符合距离要求对于 arr1[1]=5 我们有：
|5-10|=5 > d=2 
|5-9|=4 > d=2 
|5-1|=4 > d=2 
|5-8|=3 > d=2
所以 arr1[1]=5 也符合距离要求对于 arr1[2]=8 我们有：
|8-10|=2 <= d=2
|8-9|=1 <= d=2
|8-1|=7 > d=2
|8-8|=0 <= d=2
存在距离小于等于 2 的情况，不符合距离要求 故而只有 arr1[0]=4 和 arr1[1]=5 两个符合距离要求，距离值为 2

示例 2：

输入：arr1 = [1,4,2,3], arr2 = [-4,-3,6,10,20,30], d = 3
输出：2

示例 3：

输入：arr1 = [2,1,100,3], arr2 = [-5,-2,10,-3,7], d = 6
输出：1

提示：

• 1 <= arr1.length, arr2.length <= 500
• -10^3 <= arr1[i], arr2[j] <= 10^3
• 0 <= d <= 100

# 二分法
class Solution:def findTheDistanceValue(self, arr1: List[int], arr2: List[int], d: int) -> int:arr2.sort()ans = 0for x in arr1:i = bisect_left(arr2, x - d)if i == len(arr2) or arr2[i] > x + d:ans += 1return ans# 双指针法
class Solution:def findTheDistanceValue(self, arr1: List[int], arr2: List[int], d: int) -> int:arr1.sort()arr2.sort()ans = j = 0for x in arr1:while j < len(arr2) and arr2[j] < x - d:j += 1if j == len(arr2) or arr2[j] > x + d:ans += 1return ans

#思路

这题虽然是简单，但是感觉要完全的理解好像也没那么简单。我给大家分享两个题解，两种做法，大家如果看不懂建议多画图多思考。一般来说这种带公式的题目都需要做数学变化，这题的核心思路就是——对于 arr1​ 中的元素 x，如果 arr2​ 没有在 [x−d,x+d] 中的数，那么答案加一。

首先是二分法，先把 arr2从小到大排序，这样我们可以二分查找。（这是二分法的前提，数组有序）接着遍历 arr1，设 x=arr1[i]，在 arr2中二分查找 ≥x−d 的最小的数 y。如果 y 不存在，或者 y>x+d，那么说明 arr2没有在 [x−d,x+d] 中的数，答案加一。

其实第二种方法双指针法也是用的同样的判断条件，我们想象对于一个固定的x，在arr2中的所有数，要么都小于x-d，要么部分小于，剩下的都大于x+d，要么都大于x+d，只有这三种可能。那么我们通过bisect_left函数查找arr2数组中第一个大于等于x-d的数的位置。如果这个位置是等于数组长度，意味着所有数都下小于x-d，符合题意。如果不是所有数都小于x-d，那么第一个大于或等于x-d的数必须必x+d大，才满足要求。

我们接着看双指针的方法，先把 arr1和 arr2从小到大排序。遍历 arr1，设 x=arr1[i]，同时用另一个指针 j 维护最小的满足 arr2[j]≥x−d 的数的下标。如果发现 arr2[j]>x+d，那么 arr2没有在 [x−d,x+d] 中的数，答案加一。

例题6 — 2389.和有限的最长子序列

给你一个长度为 n 的整数数组 nums ，和一个长度为 m 的整数数组 queries 。

返回一个长度为 m 的数组 answer ，其中 answer[i] 是 nums 中 元素之和小于等于 queries[i] 的 子序列 的 最大 长度  。

子序列 是由一个数组删除某些元素（也可以不删除）但不改变剩余元素顺序得到的一个数组。

示例 1：

输入：nums = [4,5,2,1], queries = [3,10,21]
输出：[2,3,4]
解释：queries 对应的 answer 如下：
- 子序列 [2,1] 的和小于或等于 3 。可以证明满足题目要求的子序列的最大长度是 2 ，所以 answer[0] = 2 。
- 子序列 [4,5,1] 的和小于或等于 10 。可以证明满足题目要求的子序列的最大长度是 3 ，所以 answer[1] = 3 。
- 子序列 [4,5,2,1] 的和小于或等于 21 。可以证明满足题目要求的子序列的最大长度是 4 ，所以 answer[2] = 4 。

示例 2：

输入：nums = [2,3,4,5], queries = [1]
输出：[0]
解释：空子序列是唯一一个满足元素和小于或等于 1 的子序列，所以 answer[0] = 0 

提示：

• n == nums.length
• m == queries.length
• 1 <= n, m <= 1000
• 1 <= nums[i], queries[i] <= 106

基础代码

class Solution:def answerQueries(self, nums: List[int], queries: List[int]) -> List[int]:nums.sort()arr = [0] res = []for i, x in enumerate(nums):arr.append(x + arr[i])for j in queries:left = -1right = len(arr)while left + 1 < right:mid = left + (right - left) // 2if arr[mid] < j:left = midelse:right = midif right <= len(arr) - 1 and j == arr[right]:res.append(right)else:res.append(right - 1)return res

进阶整合代码

class Solution:def answerQueries(self, nums: List[int], queries: List[int]) -> List[int]:nums.sort()for i in range(1, len(nums)):nums[i] += nums[i - 1]  # 原地求前缀和for i, q in enumerate(queries):queries[i] = bisect_right(nums, q)  # 复用 queries 作为答案return queries

#思路

我们看题目给的样例可以发现，这题对于顺序有要求的其实就只有和答案相关的queries数组，所以nums数组是可以重排序。再读题目可以得出，要求的数组无非就是对于每个q数组的值的最大子数组长度，数组越长值越大，那么贪心的想，是不是只要nums[i]的值越小，子数组越长。所以我们可以对nums数组进行重排，由于要比对每位的和，就可以想到用前缀和的方法（第一次接触想不到很正常，博主是之前刷题遇到过类似的方法就会一下子就想到）。然后搜索匹配的前缀和就用二分搜索的方法缩短时间。

代码二是进化版，其实是写法上的升级，但是思路是一样的，不过空间和时间复杂度都会大幅度提升。对于前缀和的详细说明后面的博文会讲，大家如果自己学不明白可以去找找教学。

例题7 — 1170.比较字符串最小字母出现频次

定义一个函数 f(s)，统计 s  中（按字典序比较）最小字母的出现频次 ，其中 s 是一个非空字符串。

例如，若 s = "dcce"，那么 f(s) = 2，因为字典序最小字母是 "c"，它出现了 2 次。

现在，给你两个字符串数组待查表 queries 和词汇表 words 。对于每次查询 queries[i] ，需统计 words 中满足 f(queries[i]) < f(W) 的 词的数目 ，W 表示词汇表 words 中的每个词。

请你返回一个整数数组 answer 作为答案，其中每个 answer[i] 是第 i 次查询的结果。

示例 1：

输入：queries = ["cbd"], words = ["zaaaz"]
输出：[1]
解释：查询 f("cbd") = 1，而 f("zaaaz") = 3 所以 f("cbd") < f("zaaaz")。

示例 2：

输入：queries = ["bbb","cc"], words = ["a","aa","aaa","aaaa"]
输出：[1,2]
解释：第一个查询 f("bbb") < f("aaaa")，第二个查询 f("aaa") 和 f("aaaa") 都 > f("cc")。

提示：

• 1 <= queries.length <= 2000
• 1 <= words.length <= 2000
• 1 <= queries[i].length, words[i].length <= 10
• queries[i][j]、words[i][j] 都由小写英文字母组成

class Solution:def numSmallerByFrequency(self, queries: List[str], words: List[str]) -> List[int]:answer = []for i, x in enumerate(queries):t = min(x)c = x.count(t) # 字符串的计数器，计算t在x中出现的次数，数字也可以用queries[i] = cfor i, x in enumerate(words):t = min(x)c = x.count(t) words[i] = c# 这里如果不想重复写for循环的内容也可以写个函数 def calculate_f(s):words.sort()for t in queries:left = -1right = len(words)while left + 1 < right:mid = left + (right - left) // 2if words[mid] < t + 1:left = midelse:right = midif right > len(words) - 1:answer.append(0)else:answer.append(len(words) - right)return answer

#思路

这题相信大家看题干就可以理解，关键不在于这些七七八八的字符，而是在于比较其表示的数字，把字符串列表转化为数组。这题和上题很像，都是两个数组，一个能变顺序一个不能变。有几个易错的地方就是，我们要求的是严格大于t的数，所以我们二分的时候要比较t+1（因为都是整数，这用就一定是严格大于）以及right指向的不是直接的答案。

例题8 — 2080.区间内查询数字的频率

请你设计一个数据结构，它能求出给定子数组内一个给定值的 频率 。

子数组中一个值的 频率 指的是这个子数组中这个值的出现次数。

请你实现 RangeFreqQuery 类：

• RangeFreqQuery(int[] arr) 用下标从 0 开始的整数数组 arr 构造一个类的实例。
• int query(int left, int right, int value) 返回子数组 arr[left...right] 中 value 的 频率 。

一个 子数组 指的是数组中一段连续的元素。arr[left...right] 指的是 nums 中包含下标 left 和 right 在内 的中间一段连续元素。

示例 1：

输入：
["RangeFreqQuery", "query", "query"]
[[[12, 33, 4, 56, 22, 2, 34, 33, 22, 12, 34, 56]], [1, 2, 4], [0, 11, 33]]
输出：
[null, 1, 2]解释：
RangeFreqQuery rangeFreqQuery = new RangeFreqQuery([12, 33, 4, 56, 22, 2, 34, 33, 22, 12, 34, 56]);
rangeFreqQuery.query(1, 2, 4); // 返回 1 。4 在子数组 [33, 4] 中出现 1 次。
rangeFreqQuery.query(0, 11, 33); // 返回 2 。33 在整个子数组中出现 2 次。

提示：

• 1 <= arr.length <= 105
• 1 <= arr[i], value <= 104
• 0 <= left <= right < arr.length
• 调用 query 不超过 105 次。

class RangeFreqQuery:def __init__(self, arr: List[int]):pos = defaultdict(list)for i, x in enumerate(arr):pos[x].append(i)self.pos = posdef query(self, left: int, right: int, value: int) -> int:a = self.pos[value]return bisect_right(a, right) - bisect_left(a, left)# Your RangeFreqQuery object will be instantiated and called as such:
# obj = RangeFreqQuery(arr)
# param_1 = obj.query(left,right,value)

#思路

对于 arr 中的每个数，计算其在 arr 中的出现位置（下标）。例如 arr=[1,2,1,1,2,2]，其中数字 2 的下标为 [1,4,5]。

知道了下标，那么对于 query 来说，问题就变成了：

下标列表中，满足 left≤i≤right 的下标 i 的个数。
例如 query(3,5,2)，由于数字 2 的下标列表 [1,4,5] 中的下标 4 和 5 都在区间 [3,5] 中，所以返回 2。

把下标列表记作数组 a，由于 a 是有序数组，我们可以用二分查找快速求出：

a 中的第一个 ≥left 的数的下标，设其为 p。如果不存在，则 p 等于 a 的长度。
a 中的第一个 >right 的数的下标，设其为 q。如果不存在，则 q 等于 a 的长度。
a 中的下标在 [p,q−1] 内的数都是满足要求的，这有 q−p 个。特别地，如果 a 中没有满足要求的下标，那么 q−p=0，这仍然是正确的。

这题可能大部分人看到第一眼会比较懵，如果没有系统学过Python的同学，对类的概念不是很了解，例如示例的第一行这些东西。建议不懂的同学可以直接跳过去，就把他理解为一种系统指令，这是根据力扣后台封装这个函数的写法而改变的。后面可以自己找个时间深入学习一下类和对象这些东西。

例题9 — 3488.距离最小相等元素查询

给你一个 环形 数组 nums 和一个数组 queries 。

对于每个查询 i ，你需要找到以下内容：

• 数组 nums 中下标 queries[i] 处的元素与 任意 其他下标 j（满足 nums[j] == nums[queries[i]]）之间的 最小 距离。如果不存在这样的下标 j，则该查询的结果为 -1 。

返回一个数组 answer，其大小与 queries 相同，其中 answer[i] 表示查询i的结果。

示例 1：

输入： nums = [1,3,1,4,1,3,2], queries = [0,3,5]

输出： [2,-1,3]

解释：

• 查询 0：下标 queries[0] = 0 处的元素为 nums[0] = 1 。最近的相同值下标为 2，距离为 2。
• 查询 1：下标 queries[1] = 3 处的元素为 nums[3] = 4 。不存在其他包含值 4 的下标，因此结果为 -1。
• 查询 2：下标 queries[2] = 5 处的元素为 nums[5] = 3 。最近的相同值下标为 1，距离为 3（沿着循环路径：5 -> 6 -> 0 -> 1）。

示例 2：

输入： nums = [1,2,3,4], queries = [0,1,2,3]

输出： [-1,-1,-1,-1]

解释：

数组 nums 中的每个值都是唯一的，因此没有下标与查询的元素值相同。所有查询的结果均为 -1。

提示：

• 1 <= queries.length <= nums.length <= 105
• 1 <= nums[i] <= 106
• 0 <= queries[i] < nums.length

class Solution:def solveQueries(self, nums: List[int], queries: List[int]) -> List[int]:pos = defaultdict(list)res = []for i, x in enumerate(nums):pos[x].append(i)n = len(nums)for i in pos.values():p = i[0]i.insert(0, i[-1] - n)i.append(n + p)for i, x in enumerate(queries):a = pos[nums[x]]if len(a) == 3:res.append(-1)else:j = bisect_left(a, x)res.append(min(x - a[j - 1], a[j + 1] - x))return res

#思路

这题难在循环数组这个概念，导致整体操作很麻烦，不能像上面的题目一样，直接对计数完的字典操作，而是要做调整。而且这题感觉出题人有点故意在兜圈子，各种变量表示来表示去，一不小心就容易报错，所以大家在写的时候一定要慎重。

看示例 1，所有 1 的下标列表是 p=[0,2,4]。这里我们引入哨兵这个概念，其实就是在数组前后加上前后能循环遍历到的第一个位置。由于我们要求的是最短距离，所以不用再往后去算。

由于 nums 是循环数组：

在下标列表前面添加 4−n=−3，相当于认为在 −3 下标处也有一个 1。
在下标列表末尾添加 0+n=7，相当于认为在 7 下标处也有一个 1。
修改后的下标列表为 p=[−3,0,2,4,7]。

于是，我们在 p 中二分查找下标 i，设二分返回值为 j，那么：

p[j−1] 就是在 i 左边的最近位置。
p[j+1] 就是在 i 右边的最近位置。
两个距离取最小值，答案为

min(i−p[j−1],p[j+1]−i)
如果 nums[i] 在 nums 中只出现了一次，那么答案为 −1。

当然这题还有不是二分的求法比如单纯利用下标，大家可以自己去看看其他题解。

例题10 — 2070.每一个查询的最大美丽值

给你一个二维整数数组 items ，其中 items[i] = [pricei, beautyi] 分别表示每一个物品的 价格 和 美丽值 。

同时给你一个下标从 0 开始的整数数组 queries 。对于每个查询 queries[j] ，你想求出价格小于等于 queries[j] 的物品中，最大的美丽值 是多少。如果不存在符合条件的物品，那么查询的结果为 0 。

请你返回一个长度与 queries 相同的数组 answer，其中 answer[j]是第 j 个查询的答案。

示例 1：

输入：items = [[1,2],[3,2],[2,4],[5,6],[3,5]], queries = [1,2,3,4,5,6]
输出：[2,4,5,5,6,6]
解释：
- queries[0]=1 ，[1,2] 是唯一价格 <= 1 的物品。所以这个查询的答案为 2 。
- queries[1]=2 ，符合条件的物品有 [1,2] 和 [2,4] 。它们中的最大美丽值为 4 。
- queries[2]=3 和 queries[3]=4 ，符合条件的物品都为 [1,2] ，[3,2] ，[2,4] 和 [3,5] 。它们中的最大美丽值为 5 。
- queries[4]=5 和 queries[5]=6 ，所有物品都符合条件。所以，答案为所有物品中的最大美丽值，为 6 。

示例 2：

输入：items = [[1,2],[1,2],[1,3],[1,4]], queries = [1]
输出：[4]
解释：
每个物品的价格均为 1 ，所以我们选择最大美丽值 4 。
注意，多个物品可能有相同的价格和美丽值。

示例 3：

输入：items = [[10,1000]], queries = [5]
输出：[0]
解释：
没有物品的价格小于等于 5 ，所以没有物品可以选择。
因此，查询的结果为 0 。

提示：

• 1 <= items.length, queries.length <= 105
• items[i].length == 2
• 1 <= pricei, beautyi, queries[j] <= 109

二分方法一：前缀和

class Solution:def maximumBeauty(self, items: List[List[int]], queries: List[int]) -> List[int]:items.sort(key = lambda items: items[0])for i in range(1, len(items)):items[i][1] = max(items[i - 1][1], items[i][1])for i, q in enumerate(queries):j = bisect_right(items, q, key = lambda items: items[0])queries[i] = items[j - 1][1] if j else 0return queries

二分方法二：去除无效值

class Solution:def maximumBeauty(self, items: List[List[int]], queries: List[int]) -> List[int]:items.sort(key=lambda item: item[0])k = 0for i in range(1, len(items)):if items[i][1] > items[k][1]:  # 有用k += 1items[k] = items[i]for i, q in enumerate(queries):j = bisect_right(items, q, 0, k + 1, key=lambda item: item[0])queries[i] = items[j - 1][1] if j else 0return queries

# 思路

这题方法其实有两种，还有双指针的解法。但是我们在刷二分的题单，那还是优先想。这题和基础题型不一样的地方在于items是n*2的矩阵，相当于多了一个要比较的值。我们不可能去做两次二分，那样是没有意义的因为直接排序只能保证一个目标值有序，而items有两个，所以就要优化items，去掉无效值。而通过有序数组求最大值，我们就能想到前缀和。（也可以是去除无用信息的方法，类似单调栈，比如[3,2] 价格比 [2,4] 高，美丽值又比 [2,4] 低，那么 [3,2] 就完全不如 [2,4]，可以直接去掉。）我这里只介绍前缀和的详细思路。

示例 1 的 items=[[1,2],[3,2],[2,4],[5,6],[3,5]]，将其按照 price 从小到大排序，得

[[1,2],[2,4],[3,2],[3,5],[5,6]]
然后原地计算其 beauty 的前缀最大值，得

[[1,2],[2,4],[3, 4],[3,5],[5,6]]
注意其中 [3,2] 变成了 [3,4]，这里的 4 就是前三个物品的最大 beauty，即 max(2,4,2)=4。

算好前缀最大值后，所有 price≤q 的物品的最大 beauty，就保存在满足 price≤q 的最右边的那个物品中！

接下来我们可以二分 price>q 的第一个物品，它左边相邻物品就是 price≤q 的最后一个物品。（如果左边没有物品那么答案为 0）

例题11 — 1146.快照数组

实现支持下列接口的「快照数组」- SnapshotArray：

• SnapshotArray(int length) - 初始化一个与指定长度相等的 类数组 的数据结构。初始时，每个元素都等于 0。
• void set(index, val) - 会将指定索引 index 处的元素设置为 val。
• int snap() - 获取该数组的快照，并返回快照的编号 snap_id（快照号是调用 snap() 的总次数减去 1）。
• int get(index, snap_id) - 根据指定的 snap_id 选择快照，并返回该快照指定索引 index 的值。

示例：

输入：["SnapshotArray","set","snap","set","get"][[3],[0,5],[],[0,6],[0,0]]
输出：[null,null,0,null,5]
解释：
SnapshotArray snapshotArr = new SnapshotArray(3); // 初始化一个长度为 3 的快照数组
snapshotArr.set(0,5);  // 令 array[0] = 5
snapshotArr.snap();  // 获取快照，返回 snap_id = 0
snapshotArr.set(0,6);
snapshotArr.get(0,0);  // 获取 snap_id = 0 的快照中 array[0] 的值，返回 5

提示：

• 1 <= length <= 50000
• 题目最多进行50000 次set，snap，和 get的调用 。
• 0 <= index < length
• 0 <= snap_id < 我们调用 snap() 的总次数
• 0 <= val <= 10^9

方法一：暴力copy（过不了）

class SnapshotArray:def __init__(self, length: int):self.arr = [0] * lengthself.temp = {}self.snap_id = 0def set(self, index: int, val: int) -> None:self.arr[index] = valdef snap(self) -> int:curr = self.snap_idself.temp[curr] = self.arr.copy()self.snap_id += 1return currdef get(self, index: int, snap_id: int) -> int:t = self.tempa = t[snap_id]return a[index]# Your SnapshotArray object will be instantiated and called as such:
# obj = SnapshotArray(length)
# obj.set(index,val)
# param_2 = obj.snap()
# param_3 = obj.get(index,snap_id)

方法二：存索引用二分

class SnapshotArray:def __init__(self, length: int):self.history = defaultdict(list)self.snap_id = 0def set(self, index: int, val: int) -> None:# 如果同一个 snap_id 已经有记录，就覆盖最后一条；否则追加新记录hist = self.history[index]if hist and hist[-1][0] == self.snap_id:hist[-1] = (self.snap_id, val)else:hist.append((self.snap_id, val))def snap(self) -> int:curr = self.snap_idself.snap_id += 1return currdef get(self, index: int, snap_id: int) -> int:res = bisect_left(self.history[index], snap_id + 1, key = lambda t: t[0]) - 1# 这里也可以写((snap_id + 1, ))return self.history[index][res][1] if res >=0 else 0# Your SnapshotArray object will be instantiated and called as such:
# obj = SnapshotArray(length)
# obj.set(index,val)
# param_2 = obj.snap()
# param_3 = obj.get(index,snap_id)

# 思路

这题有点复杂，要转化的地方比较多，覆盖的知识点也多，但都是比较杂的。先说知识点。（self.xxx）这种写法算是基础知识，不会的同学建议去看书。写的时候注意代码的简洁，有些地方可以直接写self的就不用再a = self. 这样，太累赘了（但是也分题目，像这题sanp函数就不能这么写）。接着就是bisect_left函数的使用。在 Python 3.10 以后的版本，官方文档中已经给 bisect 系列函数都加上了 key 参数。即：bisect.bisect_right(a, x, lo=0, hi=len(a), *, key=None)  # 注意 key 是关键字-only 参数。所以现在我们可以这样写：j = bisect_right(items, q, key=lambda t: t[0])其中t表示的就是一个参数名，这里的意思是把列表元素（一个二元组）传给 lambda，并取它的第一个值。这里也可以写(snap_id + 1, )，因为在 Python 里，带逗号的括号表示「元组（tuple）」，这行代码创建了一个只有一个元素的元组，元素就是 snap_id + 1，

• Python 比较两个元组 (a,…) 和 (b,…) 时，会先比较第一个元素 a 和 b：

  • 若 a < b，则前者小；

  • 若 a > b，则前者大；

  • 若 a == b，才会继续比较第二个元素。

• 另外，如果一个元组是另一个的「前缀」（比如 (5,) vs (5, 100)），短的那个被认为更小

以上就是一些知识点，接下来说题目，至于这个class如何封装的感兴趣可以自己去了解，我们只要看得懂题目给的示例就行。

题意解读
调用 snap() 时，复制一份当前数组，作为「历史版本」。返回这是第几个历史版本（从 0 开始）。

调用 get(index,snapId) 时，返回第 snapId 个历史版本的下标为 index 的元素值。

暴力？
每次调用 snap()，就复制一份数组，可以吗？

不行，最坏情况下，复制 50000 次长为 50000 的数组，会「超出内存限制」。

思路
假设每调用一次 set，就生成一个快照（复制一份数组）。仅仅是一个元素发生变化，就去复制整个数组，这太浪费了。

能否不复制数组呢？

换个视角，调用 set(index,val) 时，不去修改数组，而是往 index 的历史修改记录末尾添加一条数据：此时的快照编号和 val。

举例说明：

在快照编号等于 2 时，调用 set(0,6)。
在快照编号等于 3 时，调用 set(0,1)。
在快照编号等于 3 时，调用 set(0,7)。
在快照编号等于 5 时，调用 set(0,2)。
这四次调用结束后，下标 0 的历史修改记录 history[0]=[(2,6),(3,1),(3,7),(5,2)]，每个数对中的第一个数为调用 set 时的快照编号，第二个数为调用 set 时传入的 val。注意历史修改记录中的快照编号是有序的。（一个小优化，如果快照编号重合，后面的记录覆盖前面的，减少空间浪费）
那么：

调用 get(0,4)。由于历史修改记录中的快照编号是有序的，我们可以在 history[0] 中二分查找快照编号 ≤4 的最后一条修改记录，即 (3,7)。修改记录中的 val=7 就是答案。（我解释一下，这里的意思是，如果改了，那么get给的snap_id左侧一点有数，要去找修改的值，反之就是没改，就不用动）
调用 get(0,1)。在 history[0] 中，快照编号 ≤1 的记录不存在，说明在快照编号 ≤1 时，我们没有修改下标 0 保存的元素，返回初始值 0。
关于二分查找的原理，请看视频讲解：二分查找 红蓝染色法【基础算法精讲 04】

对于 snap()，只需把当前快照编号加一（快照编号初始值为 0），返回加一前的快照编号。

3、结语

二分查找的题目到这里就告一段落啦，还有一些进阶的题目，但是太难了，感觉没必要，就先跳过去了。如果后面在比赛中见到或者其他地方遇到，觉得有意思的话我还会再更新的。

下一篇文章是二分答案，这部分题更多，可能分两次出完。

好啦，本期文章就到这里，有任何问题可以打在评论区，我看到就会回复，祝大家学习愉快，886~