04 基于sklearn的机械学习-梯度下降(上)
梯度下降
一 、为什么要用到梯度下降?
正规方程的缺陷:
非凸函数问题:损失函数非凸时,导数为0会得到多个极值点(非唯一解)
计算效率低:逆矩阵运算时间复杂度 O(n3),特征量翻倍时计算时间增为8倍(16特征需512秒)。
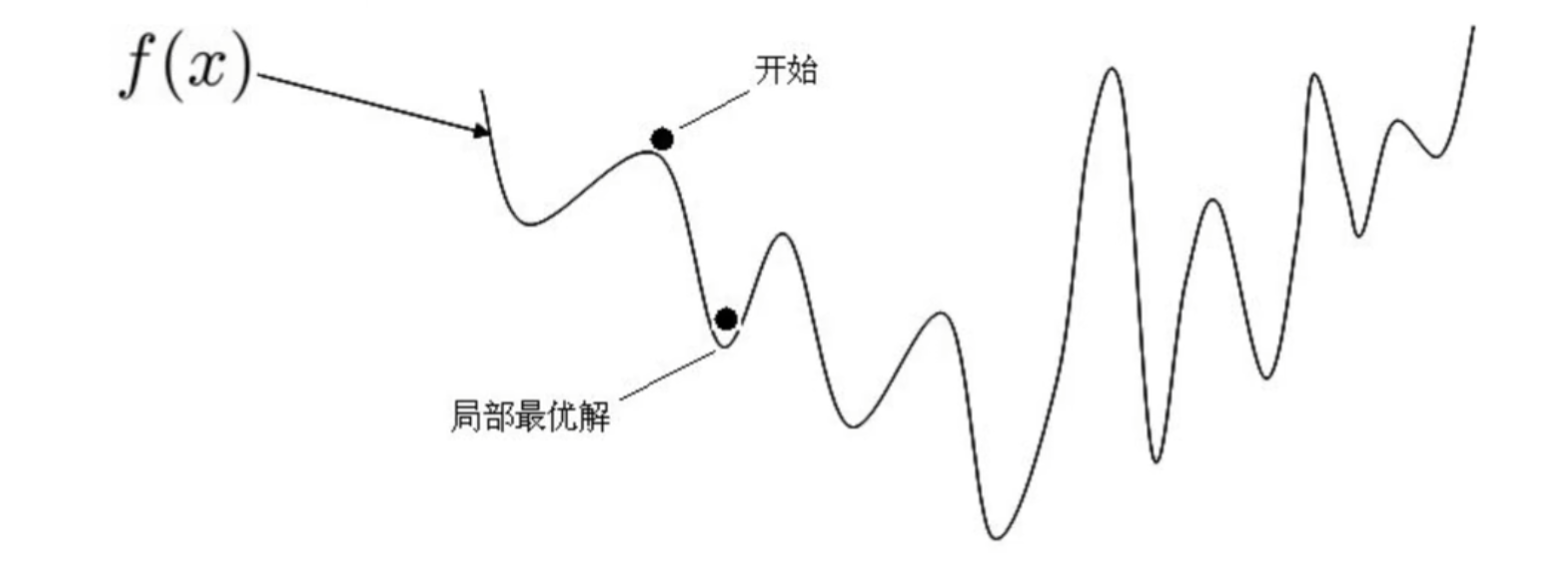
结论:梯度下降是高效求解大规模、非凸问题的通用优化算法。
二、梯度下降核心思想
目标:以最快的速度找到损失函数 loss的最小值点(最优参数 W)。
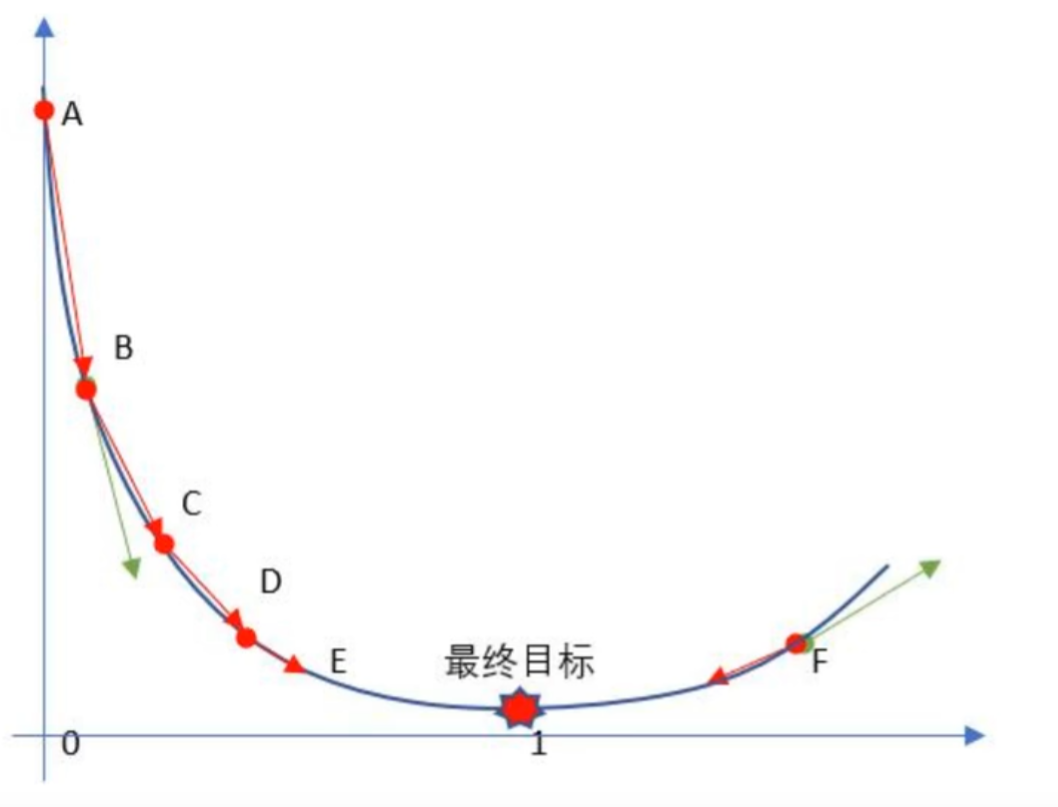
原理类比:
人在山地走向谷底,每一步沿当前最陡峭下坡方向行走。
步骤 1:判断 “下坡最陡的方向”
你低头观察脚下的地面:
左边地面微微向下倾斜,坡度较缓;
正前方地面明显向下倾斜,坡度最陡;
右边地面甚至有点向上倾斜(上坡)。
这里的 “坡度” 就是梯度—— 它不仅告诉你 “哪个方向是下坡”,还告诉你 “哪个方向下坡最陡”(梯度的方向),以及 “陡到什么程度”(梯度的大小)。
步骤 2:沿最陡方向走一小步
既然正前方下坡最陡,你就朝着正前方走一步(步长不能太大,否则可能踩空或错过转弯)。这一步对应参数更新:
方向:沿 “最陡下坡方向”(负梯度方向,因为梯度本身是 “上坡最陡” 的方向);
步长:对应 “学习率”(不能太大,否则可能直接冲到山的另一侧;也不能太小,否则走得太慢)。
步骤 3:重复调整方向,逐步逼近山脚
走完一步后,你站在新的位置,再次观察脚下的坡度(重新计算梯度),发现此时 “左前方” 变成了最陡的下坡方向。于是你调整方向,沿左前方再走一步…… 这个过程不断重复:每次都根据当前位置的坡度调整方向,走一小步,直到走到坡度几乎为 0 的平地(山脚)。
梯度 g是损失函数 loss对参数 W 的偏导数。
如果 g < 0, w 就变大 ; 如果g > 0 , w 就变小(目标左边是斜率为负右边为正 )
沿梯度反方向更新参数:W=W−α⋅g(α 为学习率)。
然后判断是否收敛(loss变化很小就收敛),如果收敛就跳出迭代,如果没收敛就再次更新参数 W...
三、单参数(w)梯度下降实现
1. 更新公式
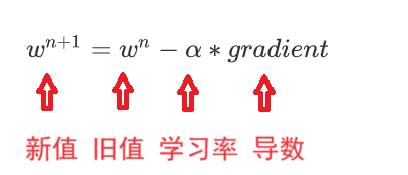
2. 参数α更新逻辑
| 位置 | 梯度 gg | 更新方向 | 操作 |
|---|---|---|---|
| 最小值左侧 | g<0 | w 增大 | w=w−(负值)→右移 |
| 最小值右侧 | g>0 | w 减小 | w=w−(正值)→左移 |
示例流程(初始 w=0.2,α=0.01):
计算 : 假设w=0.2时g=0.24 → w_new=0.2−0.01×0.24=0.1976
迭代更新直至收敛(g最小)。
# 定义总损失
def loss(w):return 10*(w**2)-15.9*w+6.5# 定义梯度
def g(w):return 20*w-15.9# 定义模型
def model(x,w):return x*w# 绘制模型
def draw_line(w):pt_x = np.linspace(0,5,100)pt_y = model(pt_x,w)plt.plot(pt_x,pt_y)#随机初始化w
w =10# 迭代
for i in range(100):print('w:',w,'loss:',loss(w))# 学习率lr = 1/(i+100)# 更新ww = w-lr*g(w)x=np.array([4.2,4.2, 2.7, 0.8, 3.7, 1.7, 3.2])
y=np.array([3.8,2.7, 2.4, 1., 2.8, 0.9, 2.9])
plt.plot(x,y,'o')
draw_line(w)
plt.show()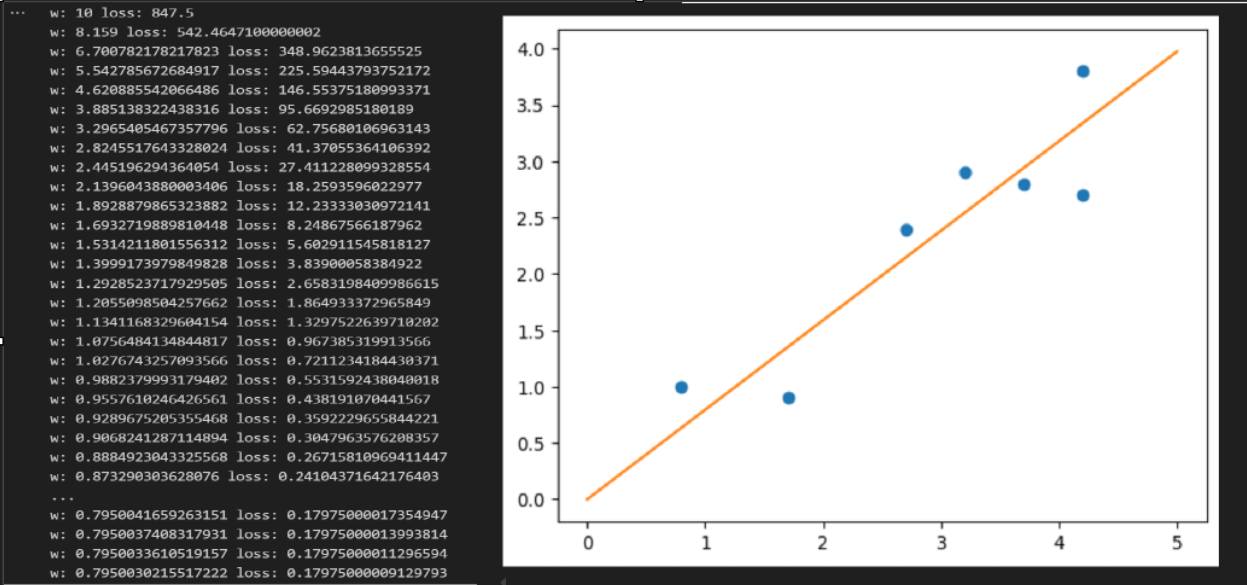
四、学习率(α)
学习率α是控制参数更新的 “步长”,是影响收敛的核心超参数:
- 过小:收敛缓慢,需大量迭代;
- 过大:可能跳过最优解,导致损失震荡甚至发散;
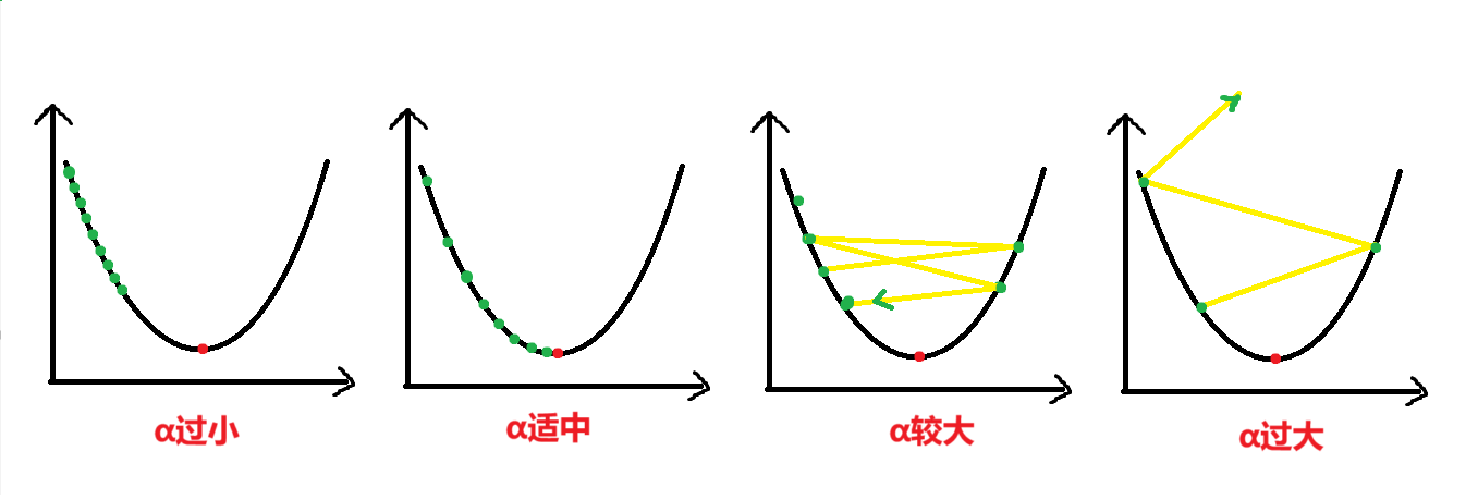
一般我们把它设置为0.1,0.01,0.001甚至更小。一般情况下学习率在迭代过程中是不变的,但是也可以设置为动态调整,即随着迭代次数逐渐变小,越接近目标W '步子'迈的更小,以更精准地找到W。
五、多参数(如 w0,w1)梯度下降实现
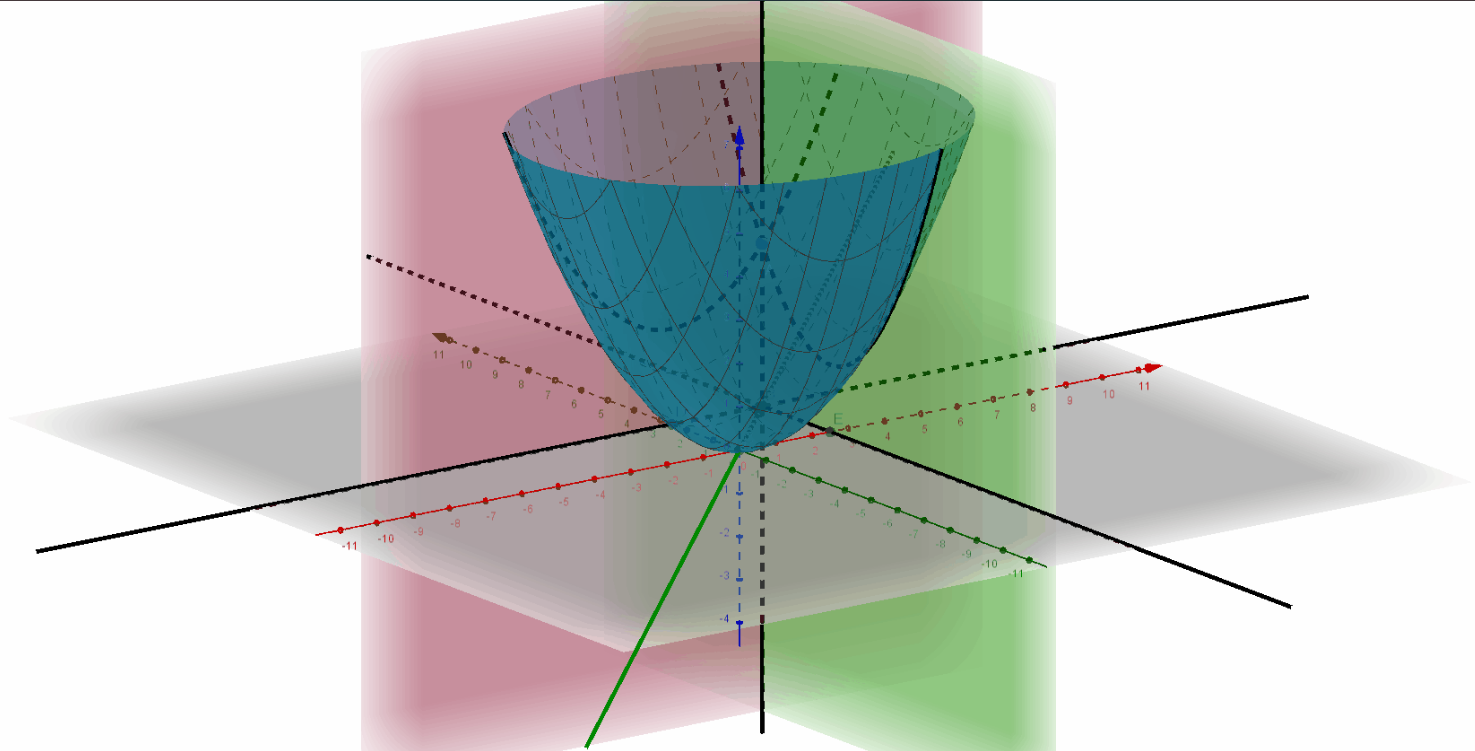
假设损失函数是有两个w1,w2特征的椎体
初始化:随机生成正态分布参数 W(如 w0,w1)。
计算梯度g:求当前 loss 的梯度 g。
更新参数:W=W−α⋅g
收敛判断:
loss变化量 < 阈值
或达到预设迭代次数(如1000次)。
终止:满足条件则输出 W;否则返回步骤2。
假设loss = (100w1 + 200w2 +1000)**2
import numpy as np
# 假设总损失
def loss(w1,w2):return (100*w1 + 200*w2 +1000)**2
# 梯度
# 以w1为参数的梯度
def g1(w1,w2):return 2*(100*w1 + 200*w2 +1000)*100
# 以w2为参数的梯度
def g2(w1,w2):return 2*(100*w1 + 200*w2 +1000)*200
# 初始化w1,w2
w1 = 10
w2 = 10
for i in range(50):print('w1:',w1,'w2:',w2,'loss:',loss(w1,w2))w1,w2 = w1-0.001*g1(w1,w2), w2-0.01*g2(w1,w2)