低通滤波器的原理以及作用

低通滤波器（Low-Pass Filter, LPF）是一种允许低频信号通过，同时衰减或阻止高频信号的电子电路或数字信号处理算法。其核心原理和作用如下：

一、工作原理
1. 频率选择性
- 低通滤波器基于频率对信号进行筛选，其传递函数在低频段增益接近1（信号无衰减），在高频段增益逐渐下降（信号被衰减）。
- 截止频率是关键参数：信号频率高于截止频率时会被显著衰减，低于截止频率时则能通过。

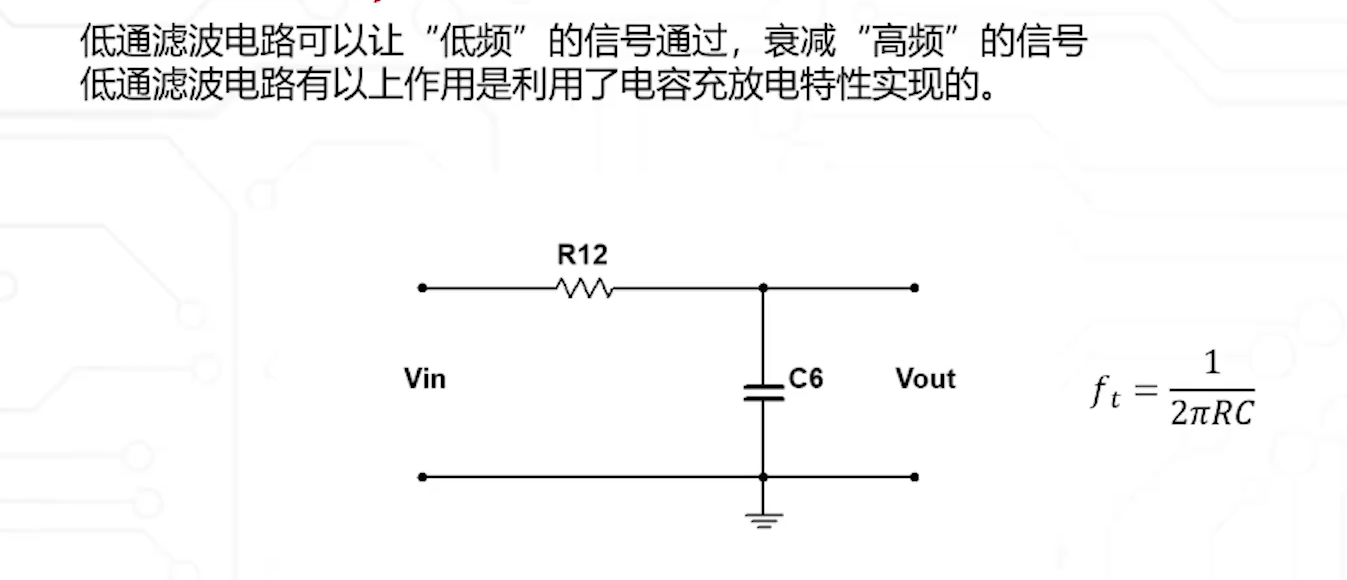
2. 实现方式 
- 模拟电路：通过电阻（R）、电容（C）、电感（L）等元件构建。  
- RC低通滤波器：由电阻和电容组成，截止频率。  

高阶滤波器（如巴特沃斯、切比雪夫）：通过多级电路实现更陡峭的滚降特性。  
-数字滤波：通过算法（如FIR或IIR）对离散信号处理，例如使用差分方程或卷积运算。

3. 数学本质* 
- 在频域中，低通滤波器是信号频谱与滤波器频率响应（如理想矩形窗或平滑过渡曲线）的乘积。  
- 时域中，滤波操作相当于信号与滤波器的冲激响应做卷积。

二、主要作用
1. 去除高频噪声
- 消除信号中的高频干扰（如电源噪声、射频干扰），保留有用的低频成分。  
- 应用示例：传感器信号去噪、音频处理中去除嘶嘶声。

2. 抗混叠（Anti-aliasing）
- 在模数转换（ADC）前，限制信号带宽以避免采样后的频谱重叠（奈奎斯特采样定理要求）。

3. 平滑信号
- 对时域信号（如脉冲、方波）进行平滑，减少突变，例如图像处理中的模糊效果或经济数据的趋势提取。

4. 保护系统带宽
- 防止高频信号进入不支持的设备（如扬声器、电机驱动电路），避免损坏或失真。

三、分类与特性
1. 按实现方式
- 模拟低通滤波器：用于连续信号，受元件精度和温度影响。  
- 数字低通滤波器：灵活可编程，但存在量化误差和延迟问题。