凸优化：常见的优化问题，偏统计视角

凸优化问题

概述

• 优化问题的一般描述
• 可微函数的一阶最优准则
• 线性规划（例如基追踪，Dantzig变量选择，Chebyshev不等式）
• 二次优化（例如最小二乘，LASSO，岭回归，投资组合，支持向量机）
• 半定规划（例如低秩矩阵恢复）

优化问题的描述

一个优化问题可以如下表示：

$$\begin{array}{rl}\min & f(x)\\ \text{s.t.}& g_i(x)\le 0,i=1,...,m\\ & h_i(x)=0,i=1,...,p\end{array}$$

• $f$是目标函数
• 优化问题的定义域：
  $$D=\text{dom}f\cap \bigcap _{i=1}^m\text{dom}{g}_i\cap \bigcap _{i=1}^p\text{dom}{h}_i$$

当$x\in D$，称$x$是可行的，所有可行点的集合称为可行集(域)（当优化问为凸优化问题时，其为凸集，因为凸函数的定义域及其下水平集是凸集，而凸集的交集为凸集）

• 在可行域上，$f(x)$的最小值称作最优值，记作$f^{\star }$

• 若$x^{\star }\in D$，并且$f(x^{\star })=f^{\star }$，称$x^{\star }$为最优解。注意，最优解可能不止一个，所有最优点构成的集合称作为最优集

• 若$x$是可行的，且满足$f(x)\le f^{\star }+ϵ$，称$x$是$ϵ-$次优解

• 若存在$R>0$，使得可行点$x$对所有可行的$y$，在满足$\Vert x-y\Vert \le R$时，有$f(x)\le f(y)$，此时称$x$为局部最优解
  

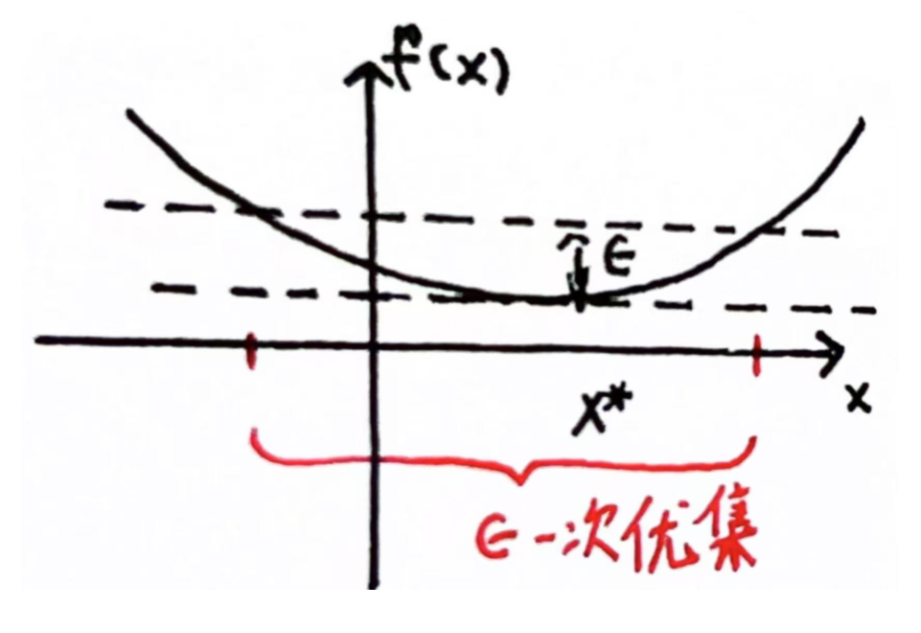
可微函数$f$的最优性准则（一阶）

对于一个目标函数可微的凸优化问题：
$$\min f(x),s.t.x\in D$$
其中$D$为可行集，当且仅当可行点$x^{\star }$满足$\nabla f^T(x^{\star })(y-x^{\star })\ge 0,\forall y\in D$，称$x^{\star }$为最优解。

对于无约束优化，上述最优性条件可化简为：
$$\nabla f(x^{\star })=0$$

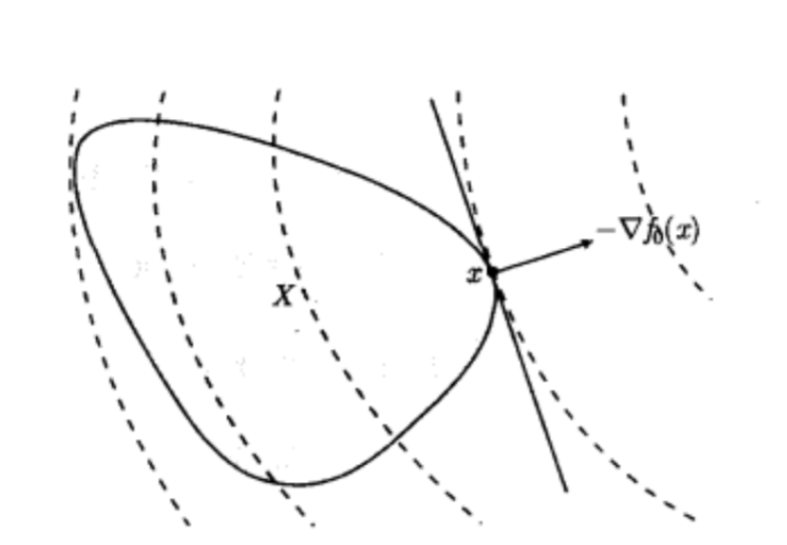
备注：
虚线为目标函数$f_0$的等值曲线（三维就是地图上常见的等高线），从支撑超平面的角度来看，$-\nabla f(x^{\star })$在$x^{\star }$处定义了可行集的一个支撑超平面，也是该函数值下降的最速方向。

凸优化问题

当$f,g_i,i=1,...,m$都是凸函数，等式约束是仿射约束（仿射函数既是凸函数也是凹函数），即$h_i(x)=a_i^{T}x-b_i,i=1,...,p$，上述优化问题是凸优化问题。对于凸优化问题，局部最小值，即是全局最小值。

备注：
一个凸优化问题是在一个凸集上极小化一个凸函数。

线性规划（目标和约束都是仿射函数）

一般形式的线性规划问题如下：

$$\begin{array}{rl}\min & c^{T}x+d\\ \text{s.t.}& Gx⪯h\\ & Ax=b\end{array}$$

其中$x\in R^n$是决策变量，$G\in R^{m\times n},A\in R^{p\times n}$

备注：
截距d可以省略

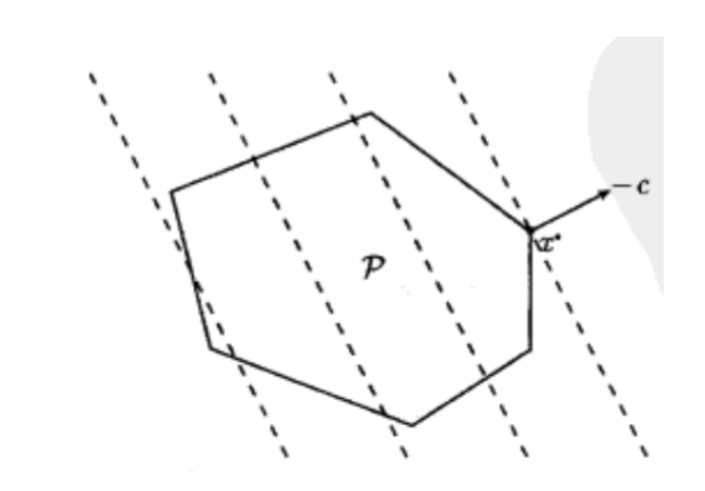
此外线性规划还有以下两种常见变化形式：

1. 不等式约束仅为决策变量的非负约束，又称之为标准形式

$$\begin{array}{rl}\min & c^{T}x\\ \text{s.t.}& x⪰0\\ & Ax=b\end{array}$$

2. 引入松弛变量$s_i$，将一般线性规划转换为标准形式的线性规划

$$\begin{array}{rl}\min & c^{T}x\\ \text{s.t.}& Gx+s=h\\ & Ax=b\\ & s⪰0\end{array}$$

接着可以将$x$表示成正部$x^{+}⪰0$和负部$x^{-}⪰0$，即$x=x^{+}-x^{-},|x|=x^{+}+x^{-}$，

$$\begin{array}{rl}\min & c^T{x}^{+}-c^T{x}^{-}\\ \text{s.t.}& G{x}^{+}-G{x}^{-}+s=h\\ & A{x}^{+}-A{x}^{-}=b\\ & s⪰0,x^{+}⪰0,x^{-}⪰0\end{array}$$

示例

基追踪（压缩感知中的一个问题）

给定$y\in R^n,X\in R^{n\times p}$，其中$p>n$，寻求欠定线性系统$X\beta =y$的稀疏解

$$\begin{array}{rlrl}& \underset{\beta }{\min }& & \Vert \beta {\Vert }_0\\ & \mathrm{subject}\mathrm{to}& & X\beta =y\end{array}$$

由于0范数不是凸函数，原问题非凸，为此可以用$l_1$范数近似0范数，此问题称为基追踪问题

$$\begin{array}{rlrl}& \underset{\beta }{\min }& & \Vert \beta {\Vert }_1\\ & \mathrm{subject}\mathrm{to}& & X\beta =y\end{array}$$

为了将其转换为线性规划问题，引入新的变量$z\in R^p$，使得每个$|{\beta }_i|$都对应一个$z_i$，那么原问题可改写如下：

$$\begin{array}{rlrl}& \underset{\beta ,z}{\min }& & 1^{T}z\\ & \mathrm{subject}\mathrm{to}& & z\ge \beta \\ & & & z\ge -\beta \\ & & & X\beta =y\end{array}$$

即写成了标准的线性规划形式。

Dantzig 变量选择

现在允许不精确的等式约束$X\beta \approx y$，Dantzig 变量选择：

$$\begin{array}{rlrl}& \underset{\beta }{\min }& & \Vert \beta {\Vert }_1\\ & \mathrm{subject}\mathrm{to}& & \Vert X^T(y-X\beta ){\Vert }_{\infty }\le \lambda \end{array}$$

其中$\lambda \ge 0$是一个惩罚参数，该约束刻画了特征与残差的相关性，使得解的特征不过度解释残差。并且该约束是LASSO对偶问题的KKT条件，该解也确保了解的稀疏性。按照上述改写成线性规划问题：

$$\begin{array}{rlrl}& \underset{z}{\min }& & 1^{T}z\\ & \mathrm{subject}\mathrm{to}& & z\ge \beta \\ & & & z\ge -\beta \\ & & & -\lambda 1\le X^T(y-X\beta )\le \lambda 1\end{array}$$

转换成线性规划问题方便求解。

Chebyshev不等式

考虑离散型随机变量$X$的概率分布：$P_i=P(X=u_i),i=1,...,n$，因此由该离散型随机变量概率分布组成的向量满足$P⪰0,1^{T}P=1$。设$u_i$是固定且已知的，但分布$P$未知，若函数$f$是$X$的函数（默认是可测函数），则$Ef={\sum }_{i=1}^{n}f(u_i)\times P_i$，是关于$P$的线性函数，若$S$是$R$的子集，那么$P(X\in S)={\sum }_{u_i\in S}{P}_i$也是$P$的线性函数。尽管$P$未知，假设知道$X$的函数期望的上下界：
$${\alpha }_i\le a_i^{T}P\le {\beta }_i,i=1,...,m$$

此时求$E{f}_0(x)=a_0^{T}P$的下界：

$$\begin{array}{rlrl}& \underset{P}{\min }& & a_0^{T}P\\ & \mathrm{subject}\mathrm{to}& & P⪰0,1^{T}P=1\\ & & & {\alpha }_i\le a_i^{T}P\le {\beta }_i,i=1,...,m\end{array}$$

该问题给出满足约束下，$E{f}_0(x)$取得最小值时的分布$P$。

二次优化

二次优化（QP）问题的描述如下：

$$\begin{array}{rlrl}& \underset{x}{\min }& & (1/2)x^{T}Px+q^{T}x+r\\ & \mathrm{subject}\mathrm{to}& & Gx⪯h\\ & & & Ax=b\end{array}$$

其中目标函数是优化变量的二次型，$P\in S_{+}^n$。

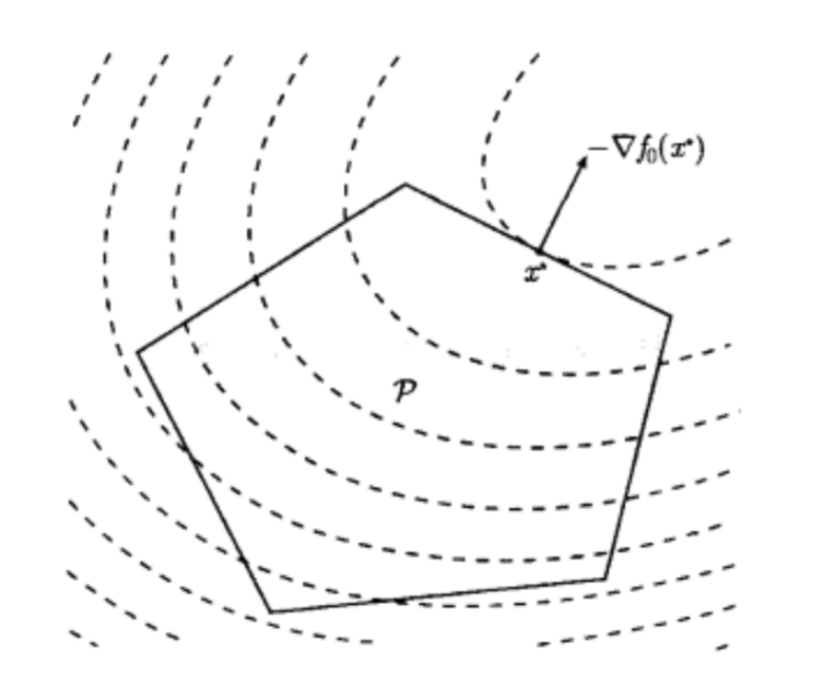
当不等式约束为也为优化变量的二次型时，称之为二次约束二次规划（QCQP）

$$\begin{array}{rlrl}& \mathrm{subject}\mathrm{to}& & (1/2)x^T{P}_{i}x+q_i^{T}x+r_i\le 0,i=1,...,m\\ & & & Ax=b\end{array}$$

其中$P_i\in S_{+}^n,i=1,...,m$。

示例

最小二乘

$$\underset{\beta }{\min }\Vert y-X\beta {\Vert }_2^2={\beta }^T{X}^{T}X\beta -2y^{T}X\beta +y^{T}y$$

当$X^{T}X⪰0$时，其是关于$\beta$的无约束二次规划问题。可以对优化变量增加约束，有约束最小二乘

$$\begin{array}{rlrl}& \underset{\beta }{\min }& & \Vert y-X\beta {\Vert }_2^2\\ & \mathrm{subject}\mathrm{to}& & l_i\le {\beta }_i\le u_i,i=1,...,p\end{array}$$

LASSO

给定$y\in R^n,X\in R^{n\times p}$，LASSO问题描述如下：

$$\begin{array}{rlrl}& \underset{\beta }{\min }& & \Vert y-X\beta {\Vert }_2^2\\ & \mathrm{subject}\mathrm{to}& & \Vert \beta {\Vert }_1\le s\end{array}$$

表示成等价的惩罚形式：
$$\underset{\beta }{\min }\frac{1}{2}\Vert y-X\beta {\Vert }_2^2+\lambda \Vert \beta {\Vert }_1$$

引入$\beta$的正部${\beta }^{+}$和负部${\beta }^{-}$，得到：

$$\begin{array}{rlrl}& \underset{{\beta }^{+},{\beta }^{-}}{\min }& & \frac{1}{2}\Vert y-X{\beta }^{+}+X{\beta }^{-}{\Vert }_2^2+\lambda 1^T{\beta }^{+}+\lambda 1^T{\beta }^{-}\\ & \mathrm{subject}\mathrm{to}& & {\beta }^{+},{\beta }^{-}\ge 0\end{array}$$

岭回归

可化简成二次约束的二次优化问题。

投资组合

现有$n$种待投资的资产，令$x_i$表示一定时期内持有资产$i$的数量（美元），$p_i$为第$i$个资产相对之前一个时期内的相对价格变动，$p\in R^n$为随机变量，均值向量$\bar{p}$和协方差$\Sigma$已知，那么有一种投资策略，在极小化总的风险（$Cov(x^{T}p)=x^T\Sigma x$）的同时，保证一定的收益即可如下转换为二次规划问题：

$$\begin{array}{rlrl}& \underset{x}{\min }& & x^T\Sigma x\\ & \mathrm{subject}\mathrm{to}& & {\bar{p}}^{T}x\ge r_{\min }(\text{表示平均收益下限})\\ & & & 1^{T}x=B(\text{表示投资总额})\\ & & & x\ge 0\end{array}$$

支持向量机

给定数据点y∈{−1,1}n,X∈Rn×py\in \{-1,1\}^n,X\in R^{n\times p}y∈{−1,1}n,X∈Rn×p，支持向量机问题可以描述如下：

$$\begin{array}{rlrl}& \underset{\beta ,{\beta }_0,\xi }{\min }& & \frac{1}{2}\Vert \beta {\Vert }_2^2+C\sum _{i=1}^n{\xi }_i\\ & \mathrm{subject}\mathrm{to}& & {\xi }_i\ge 0,i=1,\dots ,n\\ & & & y_i(x_i^T\beta +{\beta }_0)\ge 1-{\xi }_i,i=1,\dots ,n\end{array}$$

其中${\xi }_i$为松弛变量，允许有误分点，但是误分点不宜太多，因此用${\sum }_{i=1}^n{\xi }_i$控制误分程度。很明显上述问题也是一个二次规划问题。

半定规划

半定规划是线性规划在矩阵空间中通过广义不等式的推广。目标函数和约束函数均是关于矩阵的线性函数。

备注：
由于是在正常锥中定义的广义不等式，半定规划也是锥规划中正常锥取作$S_{+}^n$的特例。

其一般形式如下：

$$\begin{array}{rlrl}& \underset{x}{\min }& & c^{T}x\\ & \mathrm{subject}\mathrm{to}& & x_1{F}_1+\cdots +x_n{F}_n⪯F_0\\ & & & Ax=b\end{array}$$

其中$F_j\in S^n,j=0,...,n$，$A\in R^{m\times n},c\in R^n,b\in R^m$，

当$F_j,j=0,...,n$为对角矩阵时，其退化为一般线性规划问题。对比线性规划的标准型，可通过如下构造得到半定规划的标准型：

引入松弛变量$S$，将半定规划的线性矩阵不等式转换为等式
$$S=F_0-\sum _{i=1}^n{x}_i{F}_i,S⪰0$$

将原始变量$x$和松弛变量$S$组合成一个更大的半正定矩阵。
$$X=\left(\begin{array}{cc}\mathrm{diag}(x)& 0\\ 0& S\end{array}\right),X⪰0$$

设
$$C=\left(\begin{array}{cc}\mathrm{diag}(c)& 0\\ 0& 0\end{array}\right)$$
使得原目标函数可以转换为：
$$C\cdot X=c^{T}x$$
其中$C\cdot X=Tr(C{X}^T)$表示矩阵内积。

再来看线性等式约束的转换，设$A$的第$i$行为$a_i^T$，构造如下矩阵$A_i$：
$$A_i=\left(\begin{array}{cc}\mathrm{diag}(a_i)& 0\\ 0& 0\end{array}\right),A_i\cdot X=a_i^{T}x=b_i$$

综上可得到半定规划的标准形式：

$$\begin{array}{rlrl}& \underset{X}{\min }& & <C,X>\\ & \mathrm{subject}\mathrm{to}& & <A_i,X>=b_i,i=1,...,m\\ & & & X⪰0\end{array}$$

示例

低秩矩阵恢复

现实生活中电影评级的缺失矩阵恢复可以看作是一类低秩矩阵恢复问题。假定一个矩阵$M$，其中行变量为用户，列变量为各种电影。其中元素$M_{i,j}$是第i个用户对第j部电影的评分。显然当待评分电影较多时，不可能所有人都看完了全部的电影并评分，因此评分矩阵$M$中会有较多的缺失值。为了预测这些缺失值，可以这样考虑，首先记$M$中所有非缺失元素元素下角标的集合为$\Omega$，再假定用来恢复的矩阵$X$，当$M$中第$(i,j)$个元素未缺失时，令$X_{i,j}=M_{i,j}$，显然满足该条件的矩阵$X$有很多个，可以再作如下假定，假设两部电影类型相似，他们收获的评分也会相似，此时$M$不是列满秩。同理，假设两个用户喜欢看相同类型的电影，他们对各电影的评分也会相似，此时$M$不是行满秩。综上，$M$中可能存在低秩结构，因此寻找一个低秩矩阵$X$近似（恢复）$M$是比较合适的：

$$\begin{array}{rlrl}& \underset{X\in R^{m\times n}}{\min }& & \mathrm{rank}(X)\\ & \mathrm{subject}\mathrm{to}& & X_{ij}=M_{ij},(i,j)\in \Omega \end{array}$$

由于目标秩不是凸函数，是一个NP难的问题，类比稀疏优化中将$l_0$范数用$l_1$范数近似，而rank(X)也表示矩阵X中非零奇异值个数。因此这里可以将目标函数用$X$的核范数近似，$\Vert X{\Vert }_{\ast }={\sum }_i{\sigma }_i(X)$，矩阵$X$奇异值的和。

$$\begin{array}{rlrl}& \underset{X\in R^{m\times n}}{\min }& & \Vert X{\Vert }_{\ast }\\ & \mathrm{subject}\mathrm{to}& & X_{ij}=M_{ij},(i,j)\in \Omega \end{array}$$

接下来尽可能转换为半定规划的形式（转换为标准形式较复杂，略）。对于$(i,j)\in \Omega$，定义$A_k\in R^{m\times n}$，其第$(l,m)$个元素如下：
$$(A_k{)}_{lm}=\{\begin{array}{ll}1& \text{当}(l,m)=(i,j)\\ 0& \text{其他}\end{array}$$

因此有：
$$A_k\bullet X=\mathrm{tr}(A_k^{T}X)=X_{ij}$$

原等式约束可写作如下形式：
$$A(X)=\left(\begin{array}{c}{A}_1\bullet X\\ ⋮\\ A_p\bullet X\end{array}\right)=\left(\begin{array}{c}{M}_{i_1{j}_1}\\ ⋮\\ M_{i_p{j}_p}\end{array}\right)=b$$