python每日一题练习---简单题目

给定一个整数，写一个函数来判断它是否是 4 的幂次方。如果是，返回 true ；否则，返回 false 。

整数 n 是 4 的幂次方需满足：存在整数 x 使得 n == 4x

别拦着我 我要写个简单题 我觉得就是除以四 如果最后能是这个数除以4 结果是可以整除 那就是4的幂次方

直接来写代码 这个简单

class Solution(object):def isPowerOfFour(self, n):if n==0:return Falseif n==1:return Trueif n%4!=0:return Falsereturn True
solution=Solution()
result=solution.isPowerOfFour(6)
print(result)

首先这个忘记写范围了 然后就是不长脑子 是的 是4的幂次方那么一定是4的倍数 那么是4的倍数一定是4的幂次方吗？不是的 脑子飞走了 再改

class Solution(object):def isPowerOfFour(self, n):if n<=0:return Falseif n==1:return Truewhile n>1:if n%4!=0:return Falsen=n//4return True
solution=Solution()
result=solution.isPowerOfFour(8)
print(result)

改一下就好了 这个题很简单 我们来看一下进阶 你能不使用循环或者递归来完成本题吗？

那我们来思考一下 有没有不使用循环 也不使用递归的方法  大家一起看一下这个4的幂次方有什么特色 首先就是只有一个1 然后就是这个1是在偶数位的（从左往右是从0开始编号的）

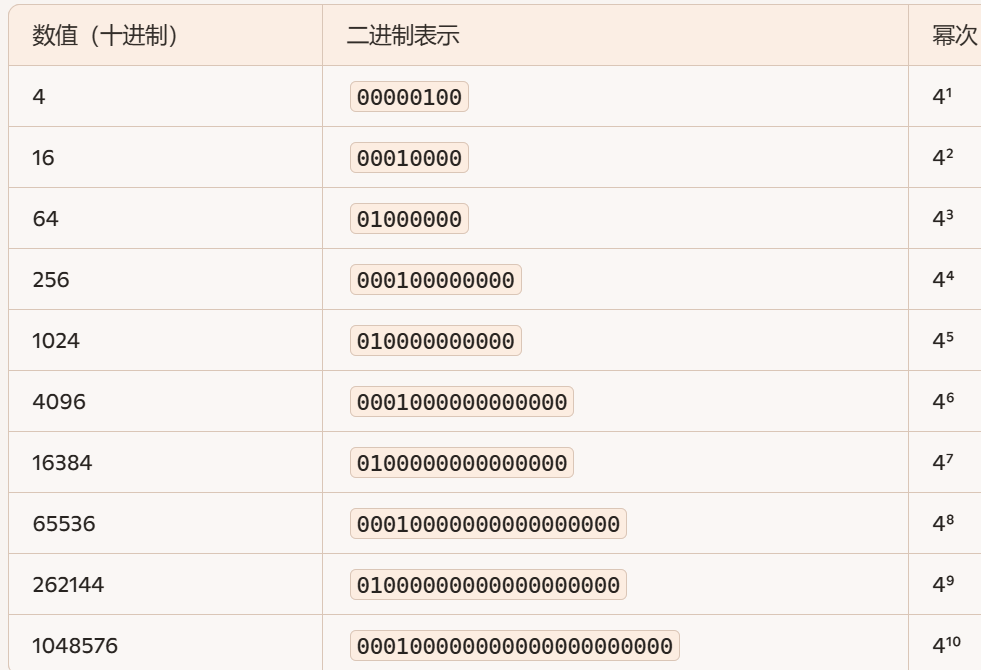
想一下只有一个是1 这个代码咋写？额这个需要开一下脑洞 就比如4 是100 3是011 那么就是二者按位与是0 只有一个只有一个1 减一之后的数字才会是除了这位之外其余都是1 所以现在这是第一个条件

但是这个不够  比如10和01也是 但是此时10并不是4的倍数 所以还要满足的是这个1要在偶数位置上 也就是100 10000这样的情况 那么这个代码咋写呢？ 

这个我也不会 大家一起学习一下这个 0xAAAAAAAA = 10101010101010101010101010101010（32位） 可以看到这些1都是在奇数位上的 那么如果这个n和这个与起来是0的话 就证明这个就是1是在偶数位上的

所以代码就是下面的：

class Solution(object):def isPowerOfFour(self, n):if n<=0:return Falseif (n & (n-1))==0 and (n & 0xAAAAAAAA) == 0:return Truereturn False
solution=Solution()
result=solution.isPowerOfFour(8)
print(result)

大家通过这个代码可以学习到关于4的幂次方的关于二进制得规律以及跟减一之间的关系  以及这个0xAAAAAAAA是什么 就很好了注意这个符号&就是会把两个数字转化为二进制的 

如果喜欢这个代码 请点个赞~