当前位置：首页 > news >正文

图论-最短路Dijkstra算法

news 2025/8/3 4:01:39

Dijkstra算法解释

迪杰斯特拉算法是基于贪心思想和单源的最短路算法。

变量解释

e[u]用来存储节点u的所有出边的终点和边权。
d[u]存u到源点s的最小距离。
vis[u]用来标记u是否出圈。

1.初始时，所有点都在集合内，初始化vis=0，d[s]=0,d[其他节点]=INT_MAX（因为要最小，所以初始化最大)。
2.从圈内选一个距离最小的点u，打上标记移出圈。
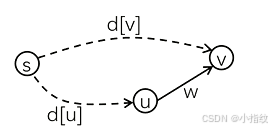
3.对u的所有出边执行操作（尝试更新邻点v的最小距离）
4.重复2，3，直到圈内为空。

缺点：
如果边权有负数就会出错。

图示：
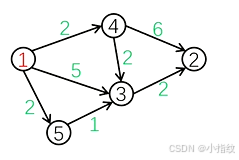
在这里插入图片描述
步骤3：

代码展示

struct edug{int v,w;//存出边的终点和边权 
}; 
vector<edge>e[N];//邻接表法建树
int d[N],vis[N];//存最小距离和访问状态
void dijkstra(int s)
{for(int i=0;i<=n;i++)d[i]=INT_MAX;//初始化为最大 d[s]=0;//起始点即源点最小距离就是0 for(int i=1;i<n;i++)//枚举n-1次{int u=0;for(int j=1;j<=n;j++)//枚举点 if(!vis[j]&&d[j]<d[u])u=j;//如果没被访问过，并且有更小的距离就更新vis[u]=1;//更新u已经被访问过for(auto x:e[u])//枚举u的每个邻点{int v=x.v,w=x.w;if(d[u]+w)<d[v])//有更小距离就更新d[v]=d[u]+w; } } } int main(){cin>>n>>m>>s;for(int i=0;i<m;i++)cin>>a>>b>>c,e[a].push_back({b,c});dijkstra(s);}

这样操作下来的时间复杂度为O( $n^2$ +m)还是比较大的，数据范围大一些就用不了。

优化

可以观察每一轮更新的点数是有限的，以及还有一些已经被pass掉的点不必要再去枚举，因此我们可以用优先队列来维护，每次只需与到源点最近的距离比较即可，不必枚举所有。
由于用pair类型创建小根堆比较复杂，所以我们可以创建一个大根堆，将参数取负，那么实际上也就是小根堆的道理。时间复杂度优化为O(mlogm)
代码展示

struct edug{int v,w;
}; 
vector<edge>e[N];
int d[N],vis[N];
priority_queue<pair<int,int>>q;
void dijkstra(int s)
{for(int i=0;i<=n;i++)d[i]=INT_MAX;d[s]=0;q.push({0,s});while(q.size()){auto t=q.top();q.pop();int u=t.second;if(vis[u])continue;//如果已经出队就不做处理 vis[u]=1;//标记已经出队 for(auto x:e[u]){int v=x.v,w=x.w;if(d[u]+w<d[v]){d[v]=d[u]+w;q.push({-d[v],v}); }}}
}

路径的记录与递归输出

struct edug{int v,w;
}; 
vector<edge>e[N];
int d[N],vis[N];
priority_queue<pair<int,int>>q;
void dijkstra(int s)
{for(int i=0;i<=n;i++)d[i]=INT_MAX;d[s]=0;q.push({0,s});while(q.size()){auto t=q.top();q.pop();int u=t.second;if(vis[u])continue;//如果已经出队就不做处理 vis[u]=1;//标记已经出队 for(auto x:e[u]){int v=x.v,w=x.w;if(d[u]+w<d[v]){d[v]=d[u]+w;pre[v]=u;//记录前驱点 q.push({-d[v],v}); }}}
}
void dfs_path(int u)
{if(u==s){cout<<u<<" ";return ;}dfs_path(pre[u]);cout<<u<<" ";}