模型选择与调优：从交叉验证到网格搜索的实践
一、交叉验证：模型评估的黄金法则
在机器学习领域，模型的泛化能力是衡量其性能的核心指标。然而，直接使用单次划分的训练集和测试集进行评估，往往会因数据随机性导致结果波动。交叉验证（Cross-Validation）通过多次划分数据，系统性地评估模型的稳定性，成为模型选择与调优的基石。
1.1 基础概念与核心思想
交叉验证的本质是通过多次重复训练 - 验证过程，将数据划分为多个子集（Fold），轮流将每个子集作为验证集，其余作为训练集。最终模型性能以所有验证结果的平均值衡量，从而降低单次划分的偶然性影响。
1.1.1 常见交叉验证方法
HoldOut 验证（Train-Test Split）
- 原理：将数据随机划分为训练集（70%-80%）和测试集（20%-30%），仅进行一次评估。
- 示例：
from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2) |
- 优缺点：
✅ 简单易行，适合大规模数据；
❌ 对数据分布敏感，易受异常值影响，小数据集评估结果不稳定。
K - 折交叉验证（K-Fold CV）
- 原理：将数据划分为 K 个互不重叠的子集，每次用 K-1 个子集训练，剩余 1 个验证，重复 K 次。
- 示例：
from sklearn.model_selection import KFold kf = KFold(n_splits=5) for train_index, test_index in kf.split(X): X_train, X_test = X[train_index], X[test_index] |
- 优缺点：
✅ 充分利用数据，结果更可靠；
❌ 计算成本随 K 增加而上升。
分层 K - 折交叉验证（Stratified K-Fold CV）
- 原理：在 K-Fold 基础上，确保每个折中各类别样本比例与原始数据一致，特别适用于类别不平衡问题。
- 示例：
from sklearn.model_selection import StratifiedKFold skf = StratifiedKFold(n_splits=5) for train_index, test_index in skf.split(X, y): X_train, X_test = X[train_index], X[test_index] |
- 应用场景：医疗诊断（如疾病预测中健康人与患者比例悬殊）、金融风控（如欺诈交易识别）等类别分布不均的场景。
1.1.2 其他交叉验证技术
- 留一法（Leave-One-Out CV）：每次保留一个样本作为验证集，适用于小数据集，但计算成本极高（需训练 N 次模型）。
- 蒙特卡罗交叉验证（Monte Carlo CV）：随机划分训练集和验证集多次，适合探索性分析。
- 时间序列交叉验证（Time Series CV）：按时间顺序划分折叠，避免未来数据泄露，适用于时序预测任务。
1.2 实战案例：鸢尾花分类的交叉验证
以经典鸢尾花数据集为例，演示分层 K - 折交叉验证的完整流程：
from sklearn.datasets import load_iris from sklearn.model_selection import StratifiedKFold from sklearn.neighbors import KNeighborsClassifier from sklearn.preprocessing import StandardScaler # 加载数据 iris = load_iris() X = iris.data y = iris.target # 初始化分层K-折交叉验证器 strat_k_fold = StratifiedKFold(n_splits=5, shuffle=True, random_state=42) knn = KNeighborsClassifier(n_neighbors=7) # 交叉验证循环 accuracies = [] for train_index, test_index in strat_k_fold.split(X, y): X_train, X_test = X[train_index], X[test_index] y_train, y_test = y[train_index], y[test_index]
# 数据标准化 scaler = StandardScaler() X_train_scaled = scaler.fit_transform(X_train) X_test_scaled = scaler.transform(X_test)
# 模型训练与评估 knn.fit(X_train_scaled, y_train) accuracies.append(knn.score(X_test_scaled, y_test)) # 输出结果 print(f"平均准确率：{np.mean(accuracies):.4f} ± {np.std(accuracies):.4f}") |
输出结果：
平均准确率：0.9667 ± 0.0298 |
二、超参数搜索：寻找模型的最优配置
超参数（Hyperparameters）是模型训练前需手动设置的参数，如 KNN 中的近邻数k、SVM 中的正则化参数C等。它们直接影响模型复杂度和泛化能力，通过系统搜索找到最优组合是模型调优的关键。
2.1 网格搜索（Grid Search）：穷举式探索
网格搜索通过定义参数候选值的网格，遍历所有可能的组合，选择交叉验证评分最高的配置。
2.1.1 核心 API 与参数设置
from sklearn.model_selection import GridSearchCV # 定义参数网格 param_grid = { 'n_neighbors': [1, 3, 5, 7, 9, 11], 'weights': ['uniform', 'distance'] } # 初始化网格搜索器 grid_search = GridSearchCV( estimator=KNeighborsClassifier(), param_grid=param_grid, cv=5, scoring='accuracy' ) # 执行搜索 grid_search.fit(X_train_scaled, y_train) |
2.1.2 结果分析与最佳模型获取
# 最佳参数组合 print("最佳参数：", grid_search.best_params_) # {'n_neighbors': 3, 'weights': 'distance'} # 最佳模型实例 best_knn = grid_search.best_estimator_ print("最佳模型：", best_knn) # KNeighborsClassifier(n_neighbors=3, weights='distance') # 交叉验证结果详情 cv_results = pd.DataFrame(grid_search.cv_results_) print("交叉验证结果：") print(cv_results[['param_n_neighbors', 'param_weights', 'mean_test_score']]) |
2.2 随机搜索（Random Search）：概率采样优化
当参数空间过大时，网格搜索的计算成本会急剧增加。随机搜索通过随机采样参数组合，在保证一定覆盖度的同时显著降低计算量，尤其适合连续型参数。
2.2.1 实现示例
from sklearn.model_selection import RandomizedSearchCV from scipy.stats import randint # 定义参数分布 param_dist = { 'n_neighbors': randint(1, 20), 'weights': ['uniform', 'distance'] } # 初始化随机搜索器 random_search = RandomizedSearchCV( estimator=KNeighborsClassifier(), param_distributions=param_dist, n_iter=50, # 采样次数 cv=5, random_state=42 ) # 执行搜索 random_search.fit(X_train_scaled, y_train) |
2.3 对比与选择
方法 | 优点 | 缺点 | 适用场景 |
网格搜索 | 穷举所有组合，结果可靠 | 计算成本高，参数空间大时不可行 | 参数较少且离散的情况 |
随机搜索 | 高效探索参数空间，适合连续参数 | 可能遗漏最优组合 | 参数较多或需平衡计算资源的场景 |
三、KNN 算法的深度调优实践
K - 近邻算法（KNN）作为最基础的分类算法之一，其性能高度依赖超参数k（近邻数）和距离度量的选择。结合交叉验证和网格搜索，可系统性优化其表现。
3.1 距离度量的选择与影响
KNN 的核心是通过距离度量寻找最近邻，常见度量方式包括：
欧式距离（Euclidean Distance）
- 公式：
- 应用场景：特征量纲一致或已标准化的数据。
曼哈顿距离（Manhattan Distance）
- 公式：
- 应用场景：城市街区等网格状数据分布。
明可夫斯基距离（Minkowski Distance）
- 公式：
- 参数：
- p=1 曼哈顿距离，p=2 欧式距离，
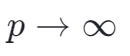切比雪夫距离。
- p=1 曼哈顿距离，p=2 欧式距离，
- 参数：
3.1.1 实战：不同距离度量的效果对比
from sklearn.metrics import accuracy_score # 定义距离度量列表 metrics = ['euclidean', 'manhattan', 'minkowski'] # 遍历不同距离度量 for metric in metrics: knn = KNeighborsClassifier(n_neighbors=5, metric=metric) knn.fit(X_train_scaled, y_train) y_pred = knn.predict(X_test_scaled) print(f"{metric} 距离准确率：{accuracy_score(y_test, y_pred):.4f}") |
输出结果：
euclidean 距离准确率：0.9737 manhattan 距离准确率：0.9474 minkowski 距离准确率：0.9737 |
3.2 超参数调优的完整流程
以鸢尾花数据集为例，演示结合分层 K - 折交叉验证和网格搜索的 KNN 调优过程：
数据预处理
标准化特征以消除量纲影响：
scaler = StandardScaler() X_scaled = scaler.fit_transform(iris.data) |
网格搜索配置
定义参数网格并执行搜索：
param_grid = { 'n_neighbors': [1, 3, 5, 7, 9, 11], 'weights': ['uniform', 'distance'], 'metric': ['euclidean', 'manhattan'] } grid_search = GridSearchCV( estimator=KNeighborsClassifier(), param_grid=param_grid, cv=5, scoring='accuracy' ) grid_search.fit(X_scaled, iris.target) |
结果分析
输出最佳参数和模型性能：
print("最佳参数：", grid_search.best_params_) print("最佳准确率：", grid_search.best_score_) |
输出结果：
最佳参数： {'n_neighbors': 3, 'weights': 'distance', 'metric': 'euclidean'} 最佳准确率： 0.9733 |
四、模型选择与调优的最佳实践
4.1 避坑指南
避免数据泄露
- 预处理步骤（如标准化）必须仅在训练集上执行，测试集使用相同参数转换。
- 交叉验证中，每个折叠的预处理需独立进行，防止验证集信息泄露。
参数范围的合理设定
- 初始探索时使用较宽的参数范围，逐步缩小搜索空间。
- 连续型参数可采用对数刻度（如C在 SVM 中的取值）。
计算资源优化
- 使用n_jobs=-1并行化网格搜索。
- 对大型数据集优先选择随机搜索。
4.2 案例：电商用户行为预测
某电商平台通过特征工程构建用户行为特征后，使用 KNN 进行购买意图分类。通过以下步骤优化模型：
特征工程
- 提取时间特征（如星期几、是否周末）。
- 价格分箱（低、中、高）。
- 标准化数值特征。
超参数调优
- 网格搜索范围：n_neighbors=[3,5,7,9]，weights=['uniform', 'distance']。
- 分层 K - 折交叉验证（n_splits=5）。
结果
- 最佳参数：n_neighbors=5，weights='distance'。
- 测试集准确率从初始的 82% 提升至 89%。
五、总结与未来方向
模型选择与调优是连接数据预处理和模型部署的关键环节。通过交叉验证确保评估的可靠性，结合网格搜索或随机搜索系统性优化超参数，可显著提升模型性能。未来，自动化机器学习（AutoML）工具将进一步简化调优流程，但理解底层原理仍是核心竞争力。
关键要点回顾：
- 交叉验证是模型评估的黄金法则，分层 K - 折尤其适合类别不平衡数据。
- 网格搜索和随机搜索是超参数调优的主流方法，需根据场景选择。
- 数据泄露和计算资源管理是实际应用中的重要考量。
通过不断实践和总结，你将逐步掌握模型选择与调优的精髓，成为数据科学领域的专家。