hot100——第九周
目录
字符串中的单词反转
寻找两个正序数组的中位数
有效的括号
最小栈
每日温度
柱状图中最大的矩形
字符串中的单词反转
解法1:双指针
一个指针i找单词的前一个空格;
收集单词;
另一个指针j指向单词的最后一个字符(i遍历的)
解法2:技巧
使用stringstream进行读取每一个单词(遇到“ ”会跳过)
class Solution
{
public:string reverseMessage(string message){int n = message.size();if (n == 0)return "";string ret;int i = n - 1, j = n - 1;while (i >= 0){// 找单词左空格while (i >= 0 && message[i] != ' ')i--;string s = message.substr(i + 1, j - i);// 为空或者s是空格就不收集if (!s.empty() && s[0] != ' ')ret += s + ' ';// 找前一个单词末尾while (i >= 0 && message[i] == ' ')i--;j = i;}// 结果不为空就要添加第一个单词的' '给去掉if (!ret.empty())ret.pop_back();return ret;}
};class Solution {
public:string reverseMessage(string message) {stringstream ss(message);string tmp,ret;while(ss>>tmp){if(ret.empty()) ret = tmp;else ret = tmp + ' ' + ret;}return ret;}
}寻找两个正序数组的中位数
解法1:枚举
可以把这两个正序数组按照从小到大的顺序排列后均分成两组(如果奇数个第一组多一个)
如果奇数个,第一组的最大值就是答案;
如果偶数个,第一组的最大值与第二组的最小值除2就是答案
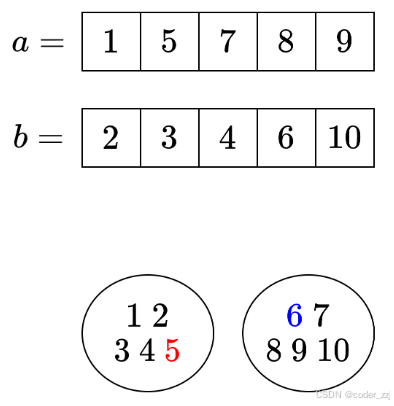
所以可以a组为例枚举a组的元素在第一组中的个数:有0,1,2,3,4,5 共6种情况;
此时对应b组在第一组的个数是:5,4,3,2,1,0 共6种情况,刚好是相反的
为了表示a组个数为0的情况与b组个数为5的情况,各自在数组中首插最小值,尾插最大值
a组枚举的指针i从0位置开始:表示当前在第一组的个数为0(i指向的元素是a组在第一组的最大值,i+1指向的元素刚好是a组在第二组的最小值);
b组枚举的指针j从倒数第二个位置开始:表示当前在第一组的个数为5(j指向的元素是b组在第一组的最大值,j+1指向的元素刚好是b组在第二组的最小值)
找满足: max(a【i】,b【j】) <= min(a【i+1】,b【j+1】)也就找到了第一组的5和第二组的6从而计算得出结果
但此时可以这样来判断:a【i】<= b【j+1】&& b【j】<= a【i+1】(可删除任意一个判断条件的=)(a【i】<= b【j+1】也就表示 min(a【i】,b【j】)<= b【j+1】另一个同理)
细节:
上面是刚好出现a,b组的元素相同,如果一个大一个小呢?
那么就要保证让大的在后面小的在前面,枚举b组时才不会越界
b组指针j的初始化?
如果a组个数n和b组个数相加是偶数,j = (n + m) / 2;
如果相加是奇数,j = (n + m + 1) / 2;
统一使用j = (n + m + 1) / 2 进行初始化
class Solution
{
public:double findMedianSortedArrays(vector<int> &nums1, vector<int> &nums2){if (nums1.size() > nums2.size()){swap(nums1, nums2);}int n = nums1.size(), m = nums2.size();// 越界处理nums1.insert(nums1.begin(), INT_MIN), nums1.push_back(INT_MAX);nums2.insert(nums2.begin(), INT_MIN);nums2.push_back(INT_MAX);int i = 0, j = (m + n + 1) / 2; //+1为了处理偶数情况// 枚举num1在第一组的个数double ret1, ret2;while (true){// 找 max(nums[i],nums2[j]) min(nums1[i+1],nums2[j+1])if (nums1[i] <= nums2[j + 1] && nums2[j] <= nums1[i + 1]){ret1 = max(nums1[i], nums2[j]);ret2 = min(nums1[i + 1], nums2[j + 1]);break;}i++;j--;}return (n + m) % 2 == 0 ? (ret1 + ret2) / 2 : ret1;}
};循环条件可以改为 b【j】> a【i+1】就继续枚举,当 b【j】<= a【i+1】时跳出循环,此时也满足 b【j+1】> a【i】:上一次循环判断过了
while (nums2[j] > nums1[i + 1])
{i++;j--;
}
ret1 = max(nums1[i], nums2[j]), ret2 = min(nums1[i + 1], nums2[j + 1]);解法2:二分
尽可能二分a组的位置使得最大程度的满足:a【i】 < b【j+1】
class Solution
{
public:double findMedianSortedArrays(vector<int> &nums1, vector<int> &nums2){// 保证值个数多的在后面if (nums1.size() > nums2.size()){swap(nums1, nums2);}int n = nums1.size(), m = nums2.size();// 越界处理nums1.insert(nums1.begin(), INT_MIN), nums1.push_back(INT_MAX);nums2.insert(nums2.begin(), INT_MIN);nums2.push_back(INT_MAX);// 二分int left = 0, right = n + 1;while (left < right){int i = (left + right + 1) / 2;int j = (n + m + 1) / 2 - i; // 根据nums1的个数确定nums2的个数if (nums1[i] < nums2[j + 1]){left = i;}else{right = i - 1;}}int pos1 = left, pos2 = (n + m + 1) / 2 - left;double ret1 = max(nums1[pos1], nums2[pos2]), ret2 = min(nums1[pos1 + 1], nums2[pos2 + 1]);return (n + m) % 2 == 0 ? (ret1 + ret2) / 2 : ret1;}
};但是由于左右插入的时间复杂度是O(N),不符合题目要求,所有还要接着思考优化方案
优化:
不插入左右值来优化时间复杂度,此时i = 0指向的位置表示a中元素在第一组有1个,不符合初始要求(a组在第一组的个数为0),此时i要减1才符合要求,j也是同理;后面二分表示j的位置就变成 j + 1 = (n + m + 1) / 2 - (i + 1)
进行二分要还注意i可能越界的问题
此时时间复杂度才是题目规定的要求:log(n+m)
class Solution
{
public:double findMedianSortedArrays(vector<int> &nums1, vector<int> &nums2){if (nums1.size() > nums2.size())swap(nums1, nums2);int n = nums1.size(), m = nums2.size();// 去掉越界处理num1和nums2下标都要减1进行修正int left = -1, right = n;while (left < right){int i = (left + right + 1) / 2;int j = (n + m + 1) / 2 - (i + 1) - 1; // 根据nums1的个数确定nums2的个数if (i < n && nums1[i] <= nums2[j + 1]){left = i;}else{right = i - 1;}}int pos1 = left, pos2 = (n + m + 1) / 2 - (left + 1) - 1;// 值就要根据位置进行判断int a1 = pos1 < 0 ? INT_MIN : nums1[pos1], b1 = pos2 < 0 ? INT_MIN : nums2[pos2];int a2 = pos1 + 1 >= n ? INT_MAX : nums1[pos1 + 1], b2 = pos2 + 1 >= m ? INT_MAX : nums2[pos2 + 1];double ret1 = max(a1, b1), ret2 = min(a2, b2);return (n + m) % 2 == 0 ? (ret1 + ret2) / 2 : ret1;}
};有效的括号
解法1:栈
遍历字符串:
遇到左括号使用栈储存;
遇到右括号去栈里面看看是否匹配(前提是栈不为空):
不匹配直接返回false,匹配就删除匹配的左扩号,继续遍历...
遍历完成返回时判断栈是否为空,不为空说明有多余的左括号没有匹配
优化:可以使用hash来储存左右括号的对应关系,这样判断是否匹配就简单点
解法2:不用栈
把s看成栈,使用变量top记录左括号:
遍历时遇到左括号,把左括号变成匹配的右括号,top++;
遇到右括号时,看看top是否为空或者 --top后top指向的括号是否匹配,不匹配直接返回false
遍历完成看看top是否等于0(等于0就说明括号队匹配完成)
class Solution
{
public:bool isValid(string s){if (s.size() % 2 != 0)return false; // 不是偶数个一定匹配不了unordered_map<char, char> hash = {{')', '('}, {']', '['}, {'}', '{'}};stack<char> st;for (auto &e : s){if (e == '(' || e == '[' || e == '{')st.push(e);else{if (st.empty() || st.top() != hash[e])return false;st.pop();}}return st.empty();// int top=0;// for(int i=0;i<s.size();i++)// {// if(s[i]=='(') s[top++]=')';// else if(s[i]=='[') s[top++]=']';// else if(s[i]=='{') s[top++]='}';// else//右括号// {// if(top==0 || s[--top]!=s[i]) return false;// }// }// //return true 如果是 "("呢// return top==0;}
};最小栈
解法1:双栈
一个栈记录正确压栈出栈,另一个最小栈记录当前最小值:如果入栈元素小于最小栈栈顶则才入栈;栈顶出栈时栈顶元素等于最小栈栈顶才出栈
解法2:栈
使用一个栈,保存pair类型:{栈元素与当前栈的最小值}
(初始化栈前先入栈 {-1,INT_MAX} 后面就不用考虑首次入栈元素的处理)
// class MinStack
// {
// public:
// stack<int> st;
// stack<int> st_min;
// MinStack()
// {
// }// void push(int val)
// {
// // 小于等于st_min栈顶的val入栈
// if (st_min.empty() || st_min.top() >= val)
// st_min.push(val);
// st.push(val);
// }// void pop()
// {
// if (st.top() == st_min.top())
// st_min.pop();
// st.pop();
// }// int top()
// {
// return st.top();
// }// int getMin()
// {
// return st_min.top();
// }
// };class MinStack
{
public:stack<pair<int, int>> st;MinStack(){// 边界处理st.push({-1, INT_MAX});}void push(int val){st.push({val, min(st.top().second, val)});}void pop(){st.pop();}int top(){return st.top().first;}int getMin(){return st.top().second;}
};解法1:栈
使用栈记录当前数字以及前面字符串信息,定义变量val表示当前遍历的数字的情况,ret表示当前遍历字符串的情况
遍历字符串:
遇到数字字符ch把它转为数字添加到val中(val = vla*10 + ch-'0' 低位添加高位的做法)
遇到字符加入到ret后面;
遇到'['就把val和ret的值放到栈中,把val,ret清空后记录新开始的情况
遇到']'就把val和ret的栈从栈里面取出来,将ret的字符串按照val的倍数进行尾插,之后把ret字符串头插到头插得到当前其中一个 数字+[]组合 的字符串
...
遍历完成此时ret就是答案进行返回
解法2:递归(没必要)
可以在遇到[进行递归得到当前[]内(已经计算完成的)字符串,与当记录的val的倍数进行尾插,之后把ret字符串头插得到当前其中一个 数字+[]组合 的字符串,清空val值往后遍历...
class Solution
{
public:string decodeString(string s){int i = 0, n = s.size();auto dfs = [&](this auto &&dfs, const string &s) -> string{int val = 0;string ret = "";while (i < n){if (s[i] >= '0' && s[i] <= '9')val = val * 10 + s[i++] - '0';else if (s[i] >= 'a' && s[i] <= 'z')ret += s[i++];else if (s[i] == '['){i++; // 递归往后走string tmp = dfs(s);string tmp1;for (int i = 0; i < val; i++)tmp1 += tmp;ret = ret + tmp1;// 初始化val = 0;i++;}else //]{return ret;}}return ret;};return dfs(s);// stack<pair<int,string>> st;// int val=0;// string ret;// for(auto& e:s)// {// if(e>='0'&&e<='9') val = val*10 + e-'0';// else if(e>='a'&&e<='z') ret+=e;// else if(e=='[')// {// st.push({val,ret});// val = 0;// ret.clear();// }// else//]// {// int a = st.top().first;// string b = st.top().second;// st.pop();// string str;// for(int i=0;i<a;i++) str+=ret;// ret = b + str;// }// }// return ret;// stack<int> s_val;// stack<string> s_string;// int val=0;// string ret;// for(auto& e:s)// {// if(e>='0'&&e<='9') val = val*10 + e-'0';// else if(e>='a'&&e<='z') ret+=e;// else if(e=='[')// {// s_val.push(val);// s_string.push(ret);// val = 0;// ret.clear();// }// else//]// {// int a =s_val.top();s_val.pop();// string b =s_string.top();s_string.pop();// string str;// for(int i=0;i<a;i++) str+=ret;// ret = b + str;// }// }// return ret;}
};每日温度
解法:单调栈
栈里保存递增/递减值(下标),当(正向/方向)遍历到的值小于/大小栈顶值就可以对栈元素的下标位置进行处理
class Solution
{
public:vector<int> dailyTemperatures(vector<int> &temperatures){int n = temperatures.size();vector<int> ret(n, 0);stack<int> st;for (int i = 0; i < n; i++){while (!st.empty() && temperatures[i] > temperatures[st.top()]){int j = st.top();st.pop();ret[j] = i - j;}st.push(i);}return ret;}
};柱状图中最大的矩形
解法:单调栈
要想找到最大的矩形,首先一定是以某个柱子为高度从而得到最大的矩形,所有问题就转化为当以某个柱子为高h时怎么求最大宽的问题?
往左边找第一次出现柱子高h1(下标为i)小于h,那么h1往后的第一个柱子的高一定大于等于h,计算矩形的高就一定是以h来计算;同理还要找到右边第一次出现柱子高h2(下标为j)小于h;这时宽度就等于 j - i -1;也就得到以当前柱子为高时的最大矩形,遍历数组找最大值
怎么快速找到当前柱子左边第一次出现的柱子?
使用单调栈,里面保存着递增的值,但遍历遇到的值大于栈顶说明栈顶就是要找到第一次出现的柱子,右边找也是同理;这也就是说要遍历两次确定当前左右的柱子,再遍历一遍计算答案共遍历三遍
class Solution
{
public:int largestRectangleArea(vector<int> &heights){int n = heights.size();vector<int> min_left(n,-1);stack<int>st1;for(int i = 0 ;i < n;i++){while(!st1.empty() && heights[i] <= heights[st1.top()]){st1.pop();}if(!st1.empty()){int j = st1.top();min_left[i] = j;}st1.push(i);}vector<int> min_right(n,n);stack<int> st2;for(int i = n-1 ;i >= 0;i--){while(!st2.empty() && heights[i] <= heights[st2.top()]){st2.pop();}if(!st2.empty()){int j = st2.top();min_right[i] = j;}st2.push(i);}int ret = 0,width = 0;for(int i = 0;i < n;i++){width = min_right[i]-min_left[i]-1;ret = max(ret,heights[i] * width);}return ret;}
};优化:当遇到的值小于等于栈顶,说明此时栈顶右边第一次出现小于的柱子找到了,可以进行填值,也就可以少一次遍历
class Solution
{
public:int largestRectangleArea(vector<int> &heights){int n = heights.size();vector<int> min_left(n,-1),min_right(n,n);//保存下标stack<int>st;for(int i = 0 ;i < n;i++){while(!st.empty() && heights[i] <= heights[st.top()]){//栈顶的右边第一个小于等于的数找到了min_right[st.top()] = i;st.pop();}if(!st.empty()){int j = st.top();min_left[i] = j;}st.push(i);}int ret = 0,width = 0;for(int i = 0;i < n;i++){width = min_right[i]-min_left[i]-1;ret = max(ret,heights[i] * width);}return ret;}
};究极优化:遇到的值小于等于栈顶,说明此时栈顶右边第一次出现小于的柱子找到了;如果此时栈的个数大于1,说明此时栈顶下一个的值就是栈顶左边第一次出现小于的柱子,此时可以进行统计求最大值啦(写的时候一定要先保存栈顶再删除栈顶,以栈顶为高进行计算)
边界处理:如果heights = {3}:为了保证只有一个柱子时能够正确返回,先在栈里面添加-1来确保柱子左边没有值时正确计算宽度;还要先在heights中添加-1:因为栈里面还有值没有计算到,添加后可以让这些值充分计算统计到(大火收汁)
class Solution
{
public:int largestRectangleArea(vector<int> &heights){stack<int> st;// 越界处理st.push(-1);// 最后一次栈里面可能还有柱子下标进行计算heights.push_back(-1);int ret = 0;for (int i = 0; i < heights.size(); i++){while (st.size() > 1 && heights[i] <= heights[st.top()]){// 栈顶的右边第一个小于等于的数找到了int right = i;// 此时的柱子高度的下标不再是i,而是栈顶int st_top = st.top();st.pop();// 现在栈顶就是出栈之前栈顶左边第一个小于等于的数int left = st.top();int width = right - left - 1;ret = max(ret, width * heights[st_top]);}st.push(i);}return ret;}
};以上便是全部内容,有问题欢迎在评论区指正,感谢观看!
