0728 哈希表折半查找树二叉树
Part 1.牛客网刷题
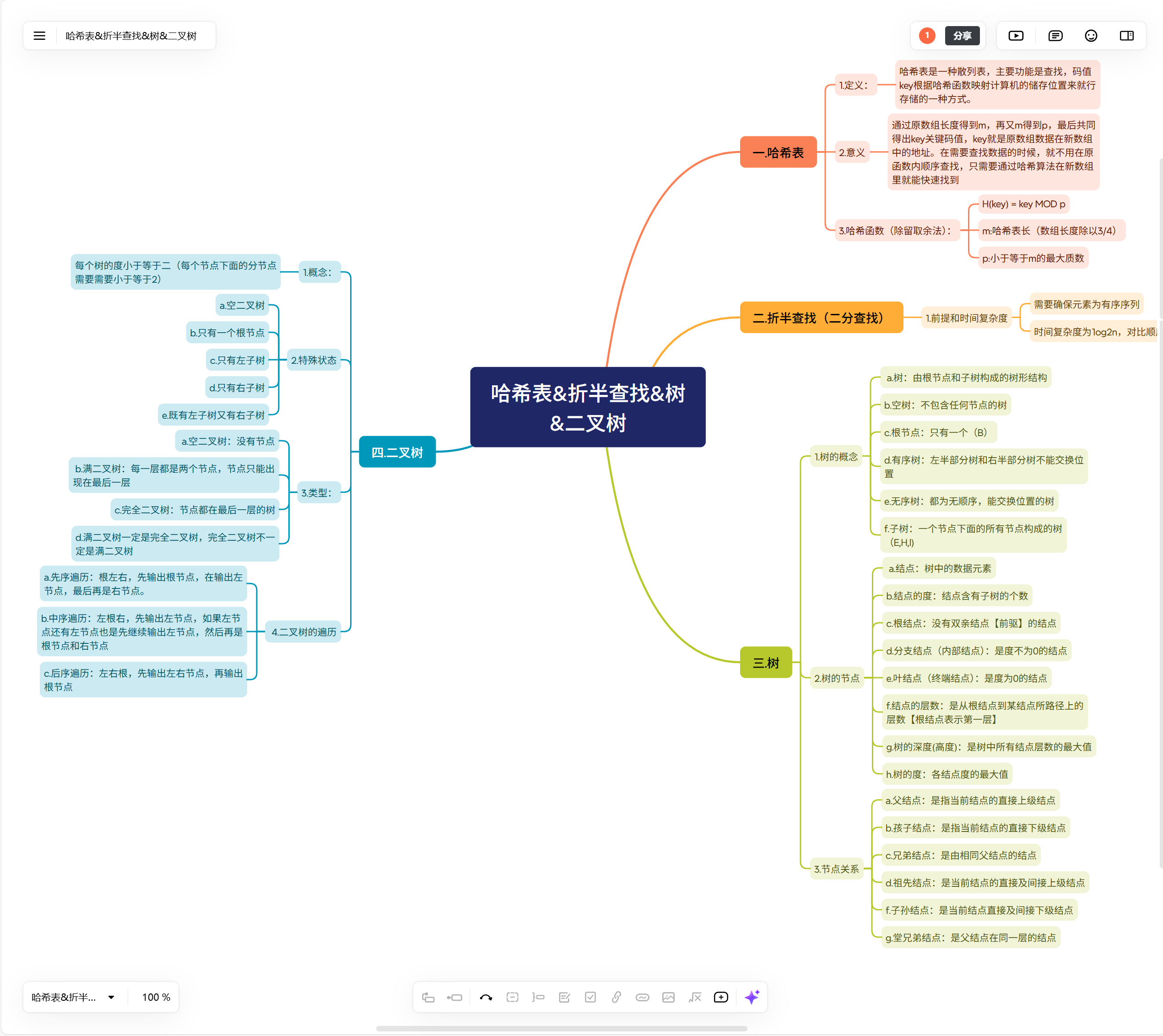
Part 2.梳理知识点,做思维导图
一.哈希表
1.定义:
哈希表是一种散列表,主要功能是查找,码值key根据哈希函数映射计算机的储存位置来就行存储的一种方式。
2.意义
通过原数组长度得到m,再又m得到p,最后共同得出key关键码值,key就是原数组数据在新数组中的地址。在需要查找数据的时候,就不用在原函数内顺序查找,只需要通过哈希算法在新数组里就能快速找到
3.哈希函数(除留取余法):
H(key) = key MOD p
m:哈希表长(数组长度除以3/4)
p:小于等于m的最大质数
4.代码
运用链表的哈希表,就是创建一个链表数组,根据原数据的地址%p得到的值,就行在对于的数组的链表插入。
#include<myhead.h>typedef struct Node
{union{int data;int len;};struct Node *next;
}*node;node create_node(int flag)
{node s = (node)malloc(sizeof(struct Node));if(s == NULL)return NULL;if(flag = 1)s->len = 0;else if(flag = 0)s->data = 0;s->next = NULL;return s;
}int prime(int m)//求最小的质数
{for(int i = m; i >= 2; i--){int count = 0;for(int j = 2; j <= sqrt(i); j++){if(i % j == 0)count++;}if(count == 0)return i;}
}void insert_head(int key,node hash[],int m)
{int p = prime(m);int sub = key % p;node head = hash[sub];node s = create_node(0);s->data = key;s->next = head->next;head->next = s;head->len++;
}void output(node hash[], int m)
{for(int i = 0; i < m; i++){printf("%d:",i);node p = hash[i]->next;while(p != NULL){printf("%-4d",p->data);p = p->next;}printf("NULL\n");}
}void search(int key,node hash[], int m)
{int p = prime(m);int sub = key % p;node head = hash[sub]->next;while(head!=NULL){if(head->data == key){printf("在\n");return;}head = head->next;}printf("不在\n");
}int main(int argc, const char *argv[])
{int arr[]={25,51,8,22,26,67,11,16,54,41};//2,创建一个哈希表//创建一个数组,存储13个头节点int len=sizeof(arr)/sizeof(arr[0]);//数组长度int m=len*4/3;node hash[m]; //m表示哈希表长度 指针数组:本质上是一个数组//对m个指针进行初始化for(int i=0;i<m;i++){hash[i]=create_node(1);}//3.数组元素根据哈希函数存到哈希表//把数组元素头插//循环输入的每个元素,插入到哈此表中for(int i=0;i<len;i++){insert_head(arr[i],hash,m);}//循环输出哈希表output(hash,m);//4.在根据哈希表查找int key;printf("请输入查找的元素:");scanf("%d",&key);search(key,hash,m);return 0;
}
二.折半查找(二分查找)
1.前提和时间复杂度
需要确保元素为有序序列
时间复杂度为1og2n,对比顺序查找要更快速
2.代码:
#include<myhead.h>int half(int *arr,int low,int high,int key)
{while(low <= high){int mid = (low+high)/2;if(arr[mid] > key)//如果比中间数要小,则往前面找high = mid -1;else if(arr[mid] < key)//如果比中间数大,则往后找low = mid + 1;elsereturn mid;}return -1;
}int main(int argc, const char *argv[])
{int arr[] = {12,34,56,67,78,87,89};int len = sizeof(arr)/sizeof(arr[0]);int key;scanf(" %d",&key);int sub = half(arr,0,len-1,key);printf("%d\n",sub);
}
三.树
1.树的概念
a.树:由根节点和子树构成的树形结构
b.空树:不包含任何节点的树
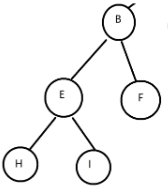
c.根节点:只有一个(B)
d.有序树:左半部分树和右半部分树不能交换位置
e.无序树:都为无顺序,能交换位置的树
f.子树:一个节点下面的所有节点构成的树(E,H,I)
2.树的节点
a.结点:树中的数据元素
b.结点的度:结点含有子树的个数
c.根结点:没有双亲结点【前驱】的结点
d.分支结点(内部结点):是度不为0的结点
e.叶结点(终端结点):是度为0的结点
f.结点的层数:是从根结点到某结点所路径上的层数【根结点表示第一层】
g.树的深度(高度):是树中所有结点层数的最大值
h.树的度:各结点度的最大值
3.节点关系
a.父结点:是指当前结点的直接上级结点
b.孩子结点:是指当前结点的直接下级结点
c.兄弟结点:是由相同父结点的结点
d.祖先结点:是当前结点的直接及间接上级结点
f.子孙结点:是当前结点直接及间接下级结点
g.堂兄弟结点:是父结点在同一层的结点
四.二叉树
1.概念:
每个树的度小于等于二(每个节点下面的分节点需要需要小于等于2)
2.特殊状态
a.空二叉树
b.只有一个根节点
c.只有左子树
d.只有右子树
e.既有左子树又有右子树
3.类型:
a.空二叉树:没有节点
b.满二叉树:每一层都是两个节点,节点只能出现在最后一层
c.完全二叉树:节点都在最后一层的树
d.满二叉树一定是完全二叉树,完全二叉树不一定是满二叉树
4.二叉树的遍历
a.先序遍历:根左右,先输出根节点,在输出左节点,最后再是右节点。
b.中序遍历:左根右,先输出左节点,如果左节点还有左节点也是先继续输出左节点,然后再是根节点和右节点
c.后序遍历:左右根,先输出左右节点,再输出根节点
5.二叉树的链式存储
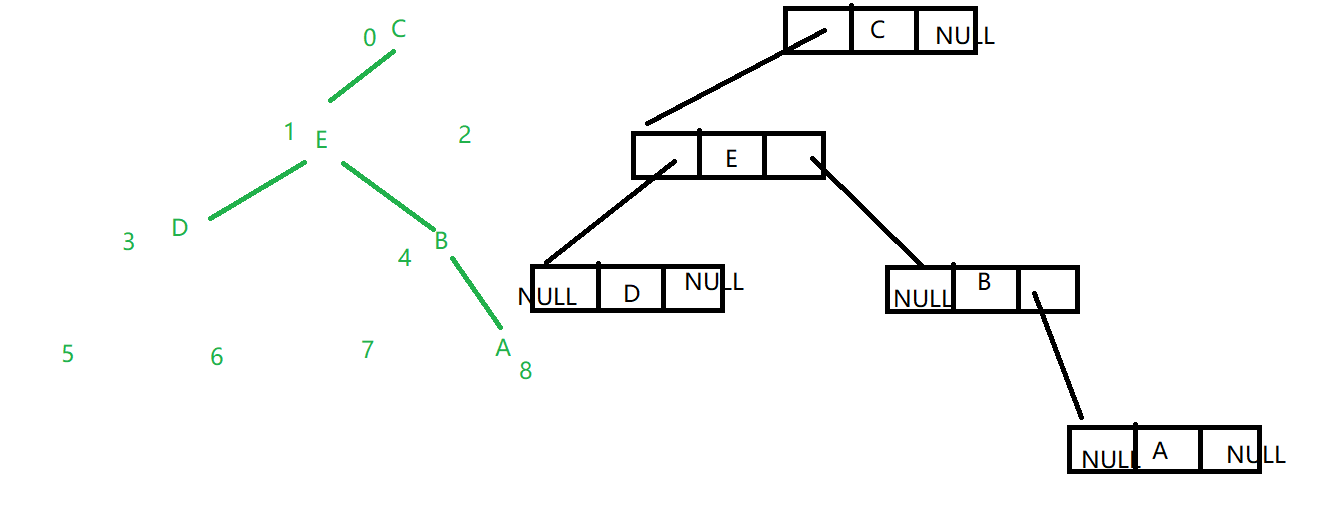
5.二叉树链式存储的代码
a.二叉树的创建
创建一个链表节点的结构体,需要存储左右两个方向的指针域和一个数据域。在创建节点时需要数据域为零,两个指针域指向空。然后用递归算法创建二叉树,创建第一层时输入数据域,左右指针域通过递归算法,调用本函数继续下一层的输入和跳转。
#include<myhead.h>typedef struct Node
{char data;struct Node *lift;struct Node *right;
}*btree;btree create_node()
{btree s = (btree)malloc(sizeof(struct Node));if(NULL == s)return NULL;s->data = 0;s->lift = s->right = NULL;return s;
}btree create_tree()
{char element;printf("请输入插入的值:");scanf(" %c",&element);if(element == '#')//输入#表示不需要下一层插入return NULL;btree tree = create_node();tree->data = element;printf("左\n");tree->lift = create_tree();printf("右\n");tree->right = create_tree();return tree;
}
b.二叉树先中后序的遍历。
void first_output(btree tree)
{if(tree == NULL)return ;printf("%c",tree->data);first_output(tree->lift);first_output(tree->right);
}void mid_output(btree tree)
{if(tree == NULL)return ; mid_output(tree->lift);printf("%c",tree->data);mid_output(tree->right);
}void last_output(btree tree)
{if(tree == NULL)return ;last_output(tree->lift);last_output(tree->right); printf("%c",tree->data);
}
