代码随想录Day32:动态规划(斐波那契数、爬楼梯、使用最小花费爬楼梯)
一、理论
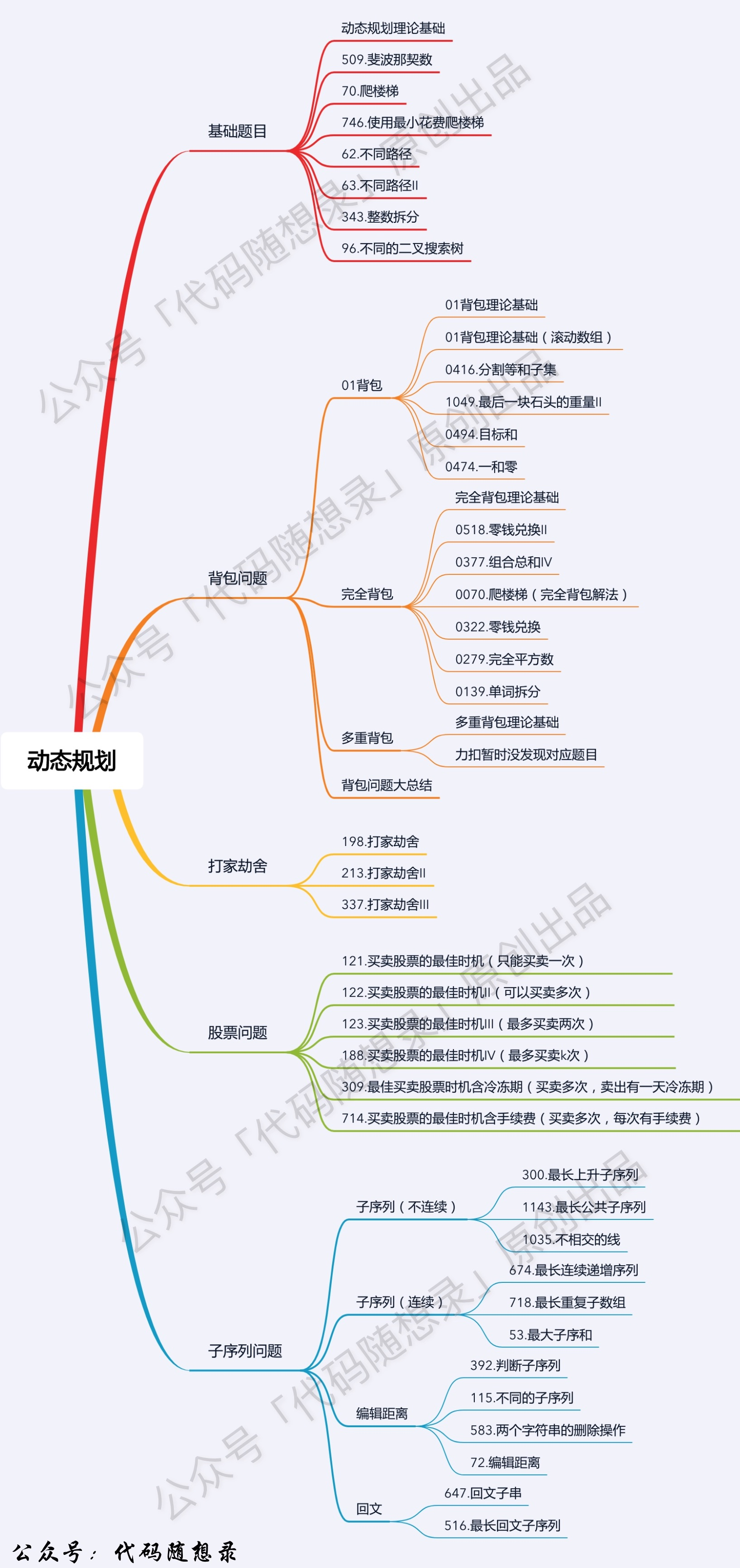
什么是动态规划(Dynamic Programming)?如果某一问题有很多重叠子问题,使用动态规划是最有效的。动态规划中每一个状态一定是由上一个状态推导出来的,这一点就区分于贪心,贪心没有状态推导,而是从局部直接选最优的,而且很多讲解动态规划的文章都会讲最优子结构啊和重叠子问题啊这些,这些东西都是教科书的上定义,晦涩难懂而且不实用,知道动规是由前一个状态推导出来的,而贪心是局部直接选最优的,对于刷题来说就够用了。
误区:状态转移公式(递推公式)只是一部分,必须掌握根本性的解题步骤。
对于动态规划问题,拆解为如下五步曲,这五步都搞清楚了,才能说把动态规划真的掌握了!
- 确定dp数组(dp table)以及下标的含义
- 确定递推公式
- dp数组如何初始化
- 确定遍历顺序
- 举例推导dp数组=打印dp数组
二、实战
509斐波那契数
509. 斐波那契数 - 力扣(LeetCode)
- 确定dp数组(dp table)以及下标的含义:dp[i]:第i个斐波那契数值
- 确定递推公式:dp[i]=dp[i-1]+dp[i-2]
- dp数组如何初始化:根据题目描述,dp[0]=dp[1]=1
- 确定遍历顺序:必须从前向后遍历
- 举例推导dp数组=打印dp数组:用来debug
package org.example.DP;public class fib509 {public int fib(int n) {//特殊情况if (n <= 1) return n;int[] dp=new int[n+1];dp[0]=0;dp[1]=1;for(int i=2;i<=n;i++){dp[i]=dp[i-1]+dp[i-2];}return dp[n];}
}
70爬楼梯
70. 爬楼梯 - 力扣(LeetCode)
爬到第一层楼梯有一种方法,爬到二层楼梯有两种方法。那么第一层楼梯再跨两步就到第三层 ,第二层楼梯再跨一步就到第三层。所以到第三层楼梯的状态可以由第二层楼梯 和 到第一层楼梯状态推导出来,那么就可以想到动态规划了。
- 确定dp数组(dp table)以及下标的含义:dp[i]:第i个台阶有几种方法
- 确定递推公式:dp[i]=dp[i-1]+dp[i-2]
- dp数组如何初始化:根据题目描述,dp[2]=2,dp[1]=1,这种定义更容易理解
- 确定遍历顺序:必须从前向后遍历
- 举例推导dp数组=打印dp数组:用来debug
package org.example.DP;public class climbStairs70 {public int climbStairs(int n) {//特殊情况if (n <= 1) return n;int[] dp=new int[n+1];dp[2]=2;dp[1]=1;for(int i=2;i<=n;i++){dp[i]=dp[i-1]+dp[i-2];}return dp[n];}
}
或者初始为 dp[0]=1;dp[1]=1;也可以,但是不太好理解,这个就是为了得出结果倒退的dp[0]定义。
746使用最小花费爬楼梯
746. 使用最小花费爬楼梯 - 力扣(LeetCode)
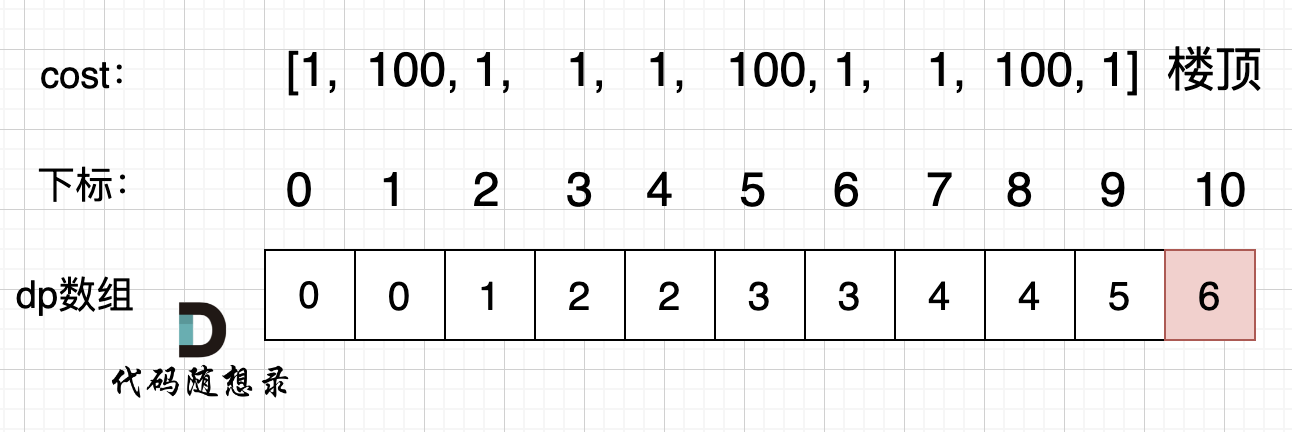
- 确定dp数组(dp table)以及下标的含义:dp[i]:到第i个台阶的最小花费
- 确定递推公式:dp[i]=min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2])
- dp数组如何初始化:根据题目描述,dp[2]=0,dp[1]=0,相当于 跳到 下标 0 或者 下标 1 是不花费体力的, 从 下标 0 下标1 开始跳就要花费体力了。
- 确定遍历顺序:必须从前向后遍历
- 举例推导dp数组=打印dp数组:用来debug
package org.example.DP;public class minCostClimbingStairs746 {public int minCostClimbingStairs(int[] cost) {int n = cost.length;int[] dp = new int[n + 1];//从下标为 0 或下标为 1 的台阶开始,支付费用为0dp[0] = 0;dp[1] = 0;// 计算到达每一层台阶的最小费用for (int i = 2; i <= n; i++) {dp[i] = Math.min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);}return dp[n];}
}
