[1+2cos(ω)+2cos(2ω)+……+2cos(Nω)]sin(ω/2)=sin[(ω+1/2)N]
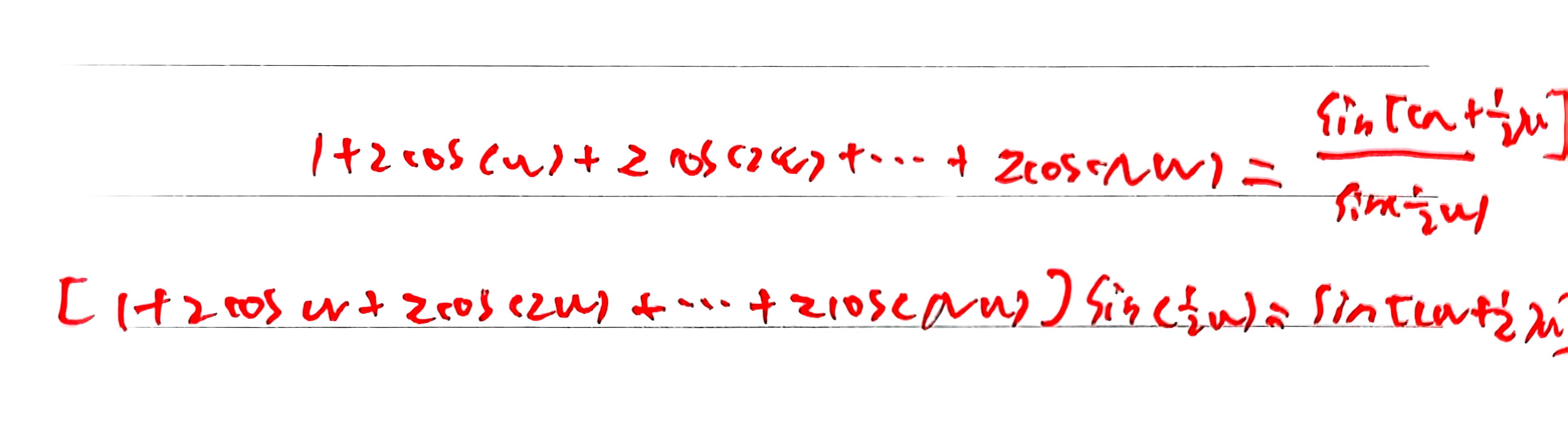
这个公式在Fourier变换的很多地方都会用到。
比如,Sa函数的积分/求和证明:

这个公式的证明就像麻袋上一拉就开的编织绳,一项化解了后面每一项都逐次化解。
不过我暂时忘了咋证了......持续更新中……
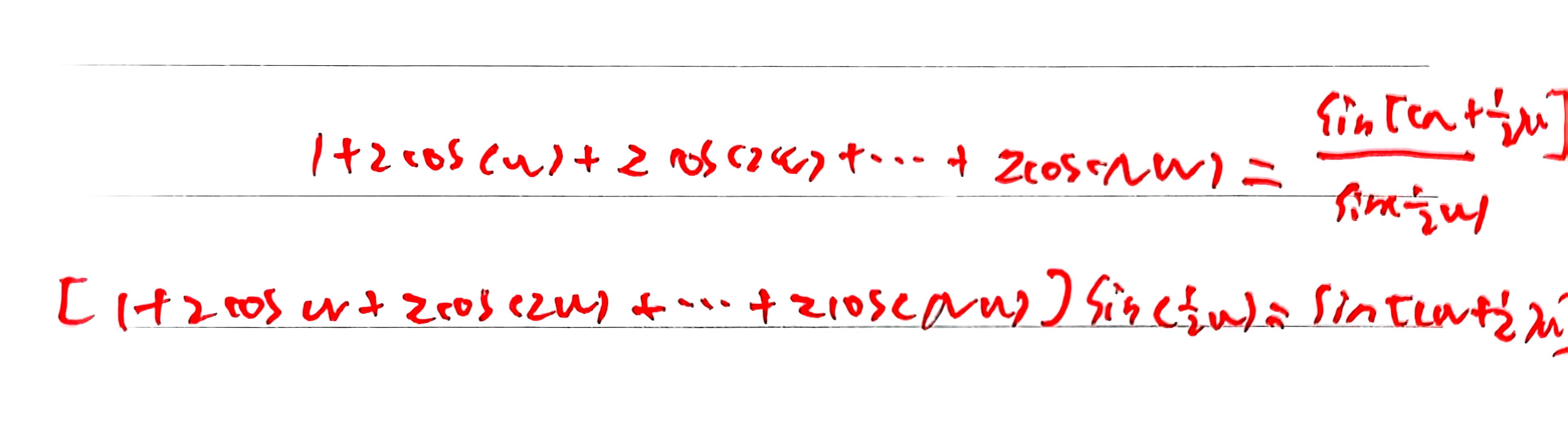
这个公式在Fourier变换的很多地方都会用到。
比如,Sa函数的积分/求和证明:

这个公式的证明就像麻袋上一拉就开的编织绳,一项化解了后面每一项都逐次化解。
不过我暂时忘了咋证了......持续更新中……