贝叶斯决策论
目录
一、引言与基础知识
1、条件概率
2、全概率公式
3、贝叶斯公式
4、先验概率、类条件概率、后验概率
5、例子
二、基于最小错误率的贝叶斯决策
三、基于最小风险的贝叶斯决策
四、例题
五、最大似然比的贝叶斯决策
六、拒绝判决
要想用贝叶斯决策论去进行一个分类器的设计,那么就必须要知道两个先级的条件,就是你必须要满足这两个条件:
①各类别的总体概率分布【知道它大概这个数据,它是属于一个高斯分布或者属于一个什么什么分布】
②要决策分类的类别数是已知的【二分类?三分类?】
一、引言与基础知识
1、条件概率

2、全概率公式
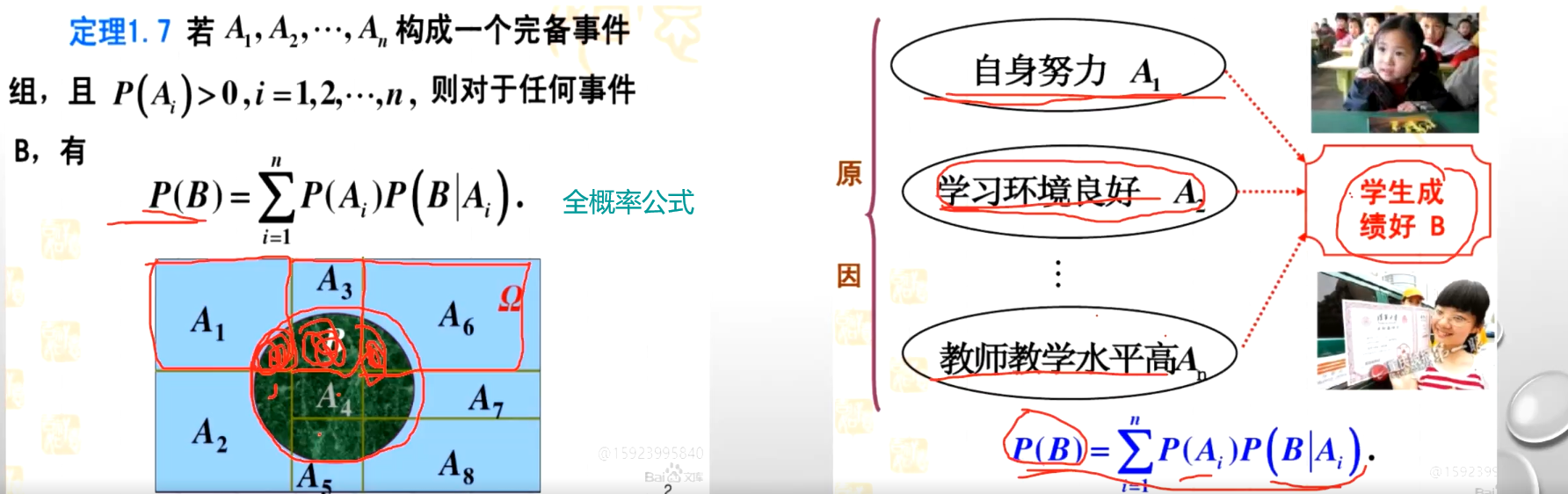
比方说自身努力学习环境良好,教师水平高等等,那么这些因素构成了学习生成绩的一个完备事件组。那么这个学生的成绩 B 它的概率有多大,它应该等于是学生自身努力的概率乘上在学生努力的情况下学习成绩好的概率 + 学习环境良好的概率乘上一个学习环境良好的情况下成绩好的概率............一次加一次加加到这里构成了一个学生成绩好的整体概率,这就是全概率公式。
3、贝叶斯公式
原来是推测学习成绩好的概率,但是现在我告诉你某一个学生,他的学习成绩就是良好的,这个结果已经发生了。现在我来探讨它是由于学习环境良好所导致的学生学习成绩好的概率有多大?也就是它是由这个因素影响的有多大,那怎么算?

学习成学习环境好的概率乘上一个学习环境好的情况下学习成绩好的概率比上我整个学习成绩好的概率
4、先验概率、类条件概率、后验概率

比方说一个村 a 村,它有100个村民。那么现在这100个村民中有90%的人要得一种病,有10%的人不患这种病。,现在小明这个人是来自于 a 村的,小明是有病的还是没病的?
我们觉得因为这个村子有90%是有病10%是没病的,那这种情况下我们就知道我们判断小明是有病的,这种推断叫做先验概率

比方说现在这一个病有一个症状叫做发热。在这个90个有病的人中,发热的概率是80%,有20%是不发热的。在没病的人中,有10%是发热的,90%是不发热的。这个时候小明不发热,这个时候我们认为小明是有病的还是没病的?
我们可能会认为小明是没有病的,因为小明他的这个类条件概率比较大。

第二次,我判断小明是没有病的,因为同时会受到我们的先验概率和内条件概率的影响。那么我们要同时考虑到它的先验概率和类条件概率,我们就可以用后验概率来表示。
所以说贝耶斯公式的一个另外一个解释等于是后验概率。后验概率等于先验概率乘上一个类条件的概率,除上一个全概率公式。物理含义就是小明不发热,那么它属于有病的一个类别的概率和它属于无病类别的一个概率。
所以使用贝叶斯决策,需要已知以下条件:

5、例子




据贝叶斯决策,该病人未患病的概率更高,医生更可能判断为「未患血液病」。【基于最小错误率准则】
二、基于最小错误率的贝叶斯决策



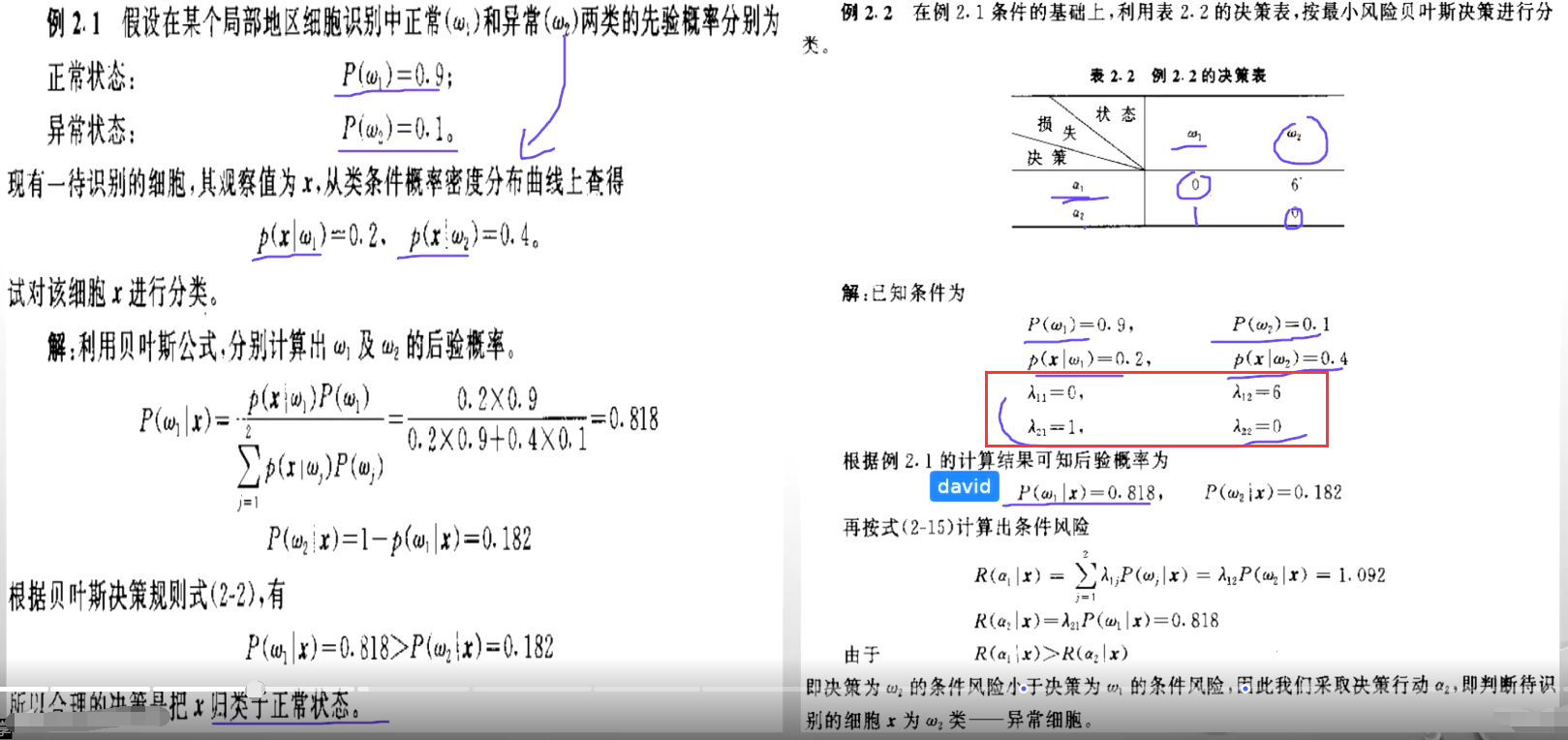
三、基于最小风险的贝叶斯决策
最小错误率的贝叶斯决策,它有一个不足是我们这个做了决策之后如果决策是错误的,那么它的风险没有考虑。

比方说以医生根据白细胞的浓度来判断一个人是不是具有血液疾病为例子。医生会犯两种错误,医生可能会犯两种错误,一种错误是本来这个人没有病,但是我判断为有病了。这是一种,还有一种是本来这个人他是有病的,但是判断成没有病了,这是两类错误。这两类错误在被最小错误率的贝叶斯决策中,他认为是等价的;但是把没有病判断成为有病,那么病人可以做进一步的检查,这个损失不是特别大,但是如果这个人一旦他是真正的有病的,但是你医生认为他是没有病的,那这个时候损失就比较严重,会耽误治疗。
计算基于风险的贝叶斯决策需要一个损失矩阵


条件风险越小,那么我的整体风险就越小,他们是一致优的


四、例题
五、最大似然比的贝叶斯决策
任何一个贝耶斯决策,它都可以写成自然比的形式



似然比在进行多分类的时候很有用:能够有效量化不同类别对观测数据的支持程度,进而辅助做出准确的分类决策

可以在同一尺度下比较不同类别对观测数据的解释能力。
假设在图像分类任务中,要区分猫、狗、兔子三种动物,通过计算似然比,能判断出当前图像的特征更符合哪一类动物的特征分布,即哪一类动物使得该图像出现的概率相对更大。
六、拒绝判决
拒绝判决的实质是什么?具体判决的实质它就是最小风险贝叶斯决策的一个变种。怎么理解,比方说有一个人去看病,那么这个人做的检查不够,医生说我不能知道你患了什么病,也就是拒绝做判断,它所带来的风险比我做任何一个判断所带来的风险都要小,那么它就执行拒绝判决的实质,它就是一个最小风险的一次决策。


七、代码实现
实现了一个简单的朴素【假设特征独立】贝叶斯分类器,用于二分类任务(预测结果为 0 或 1,代码中用 "ng" 表示 0,"ok" 表示 1)
import numpy as npclass BayesModel():"""朴素贝叶斯分类器实现,用于二分类任务(0表示ng,1表示ok)"""def __init__(self):super(BayesModel, self).__init__()self.ng_result = [] # 存储每个特征在类别0(ng)下的条件概率 [(P(特征=0|ng), P(特征=1|ng)), ...]self.ok_result = [] # 存储每个特征在类别1(ok)下的条件概率 [(P(特征=0|ok), P(特征=1|ok)), ...]self.ng = 0.0 # 先验概率 P(ng):样本属于类别0的概率self.ok = 0.0 # 先验概率 P(ok):样本属于类别1的概率def probability(self, a, b):"""计算两个互斥事件的概率参数:a: 事件A的数量b: 事件B的数量(与A互斥)返回:(p_a, p_b): 事件A和B的概率"""p_a = a / (a + b) # 事件A的概率p_b = 1 - p_a # 事件B的概率(因A和B互斥且穷尽所有可能)return p_a, p_bdef fit(self, x, y):"""训练模型:计算先验概率和条件概率参数:x: 特征数据,形状为 [样本数, 特征数]y: 标签数据,形状为 [样本数, 1],值为0或1"""columns = x.shape[1] # 获取特征的数量data = np.c_[x, y] # 将特征和标签合并成一个数组,方便按标签筛选数据# 按标签筛选数据ng_data = data[(data[:, -1] == 0)] # 筛选出标签为0(ng)的所有样本ok_data = data[(data[:, -1] == 1)] # 筛选出标签为1(ok)的所有样本# 计算先验概率:P(ng)和P(ok)ng_len = ng_data.shape[0] # 类别0的样本数量ok_len = ok_data.shape[0] # 类别1的样本数量self.ng, self.ok = self.probability(ng_len, ok_len) # 计算先验概率# 计算每个特征在不同类别下的条件概率for i in range(columns): # 遍历每个特征# 计算类别0中,第i个特征取0和1的样本数ng_len_ng = ng_data[(ng_data[:, i] == 0)].shape[0] # 特征i为0的样本数ng_len_ok = ng_len - ng_len_ng # 特征i为1的样本数(总样本数减去为0的数量)# 计算类别1中,第i个特征取0和1的样本数ok_len_ng = ok_data[(ok_data[:, i] == 0)].shape[0] # 特征i为0的样本数ok_len_ok = ok_len - ok_len_ng # 特征i为1的样本数# 计算并存储条件概率# ng_result[i] = (P(特征i=0|ng), P(特征i=1|ng))self.ng_result.append(self.probability(ng_len_ng, ng_len_ok))# ok_result[i] = (P(特征i=0|ok), P(特征i=1|ok))self.ok_result.append(self.probability(ok_len_ng, ok_len_ok))def predict(self, data_data):"""预测样本类别参数:data_data: 待预测的样本数据,形状为 [样本数, 特征数]返回:list_result: 预测结果列表,每个元素为0或1"""list_result = [] # 存放所有样本的预测结果for datas in data_data: # 遍历每个待预测样本# 初始化后验概率:从先验概率开始计算ng_prob = self.ng # 初始化P(ng|特征)为P(ng)ok_prob = self.ok # 初始化P(ok|特征)为P(ok)# 遍历样本的每个特征,更新后验概率for index, data in enumerate(datas):if data == 0:# 特征值为0时,乘以该特征在对应类别下为0的条件概率ng_prob *= self.ng_result[index][0] # 乘以 P(特征i=0|ng)ok_prob *= self.ok_result[index][0] # 乘以 P(特征i=0|ok)else:# 特征值为1时,乘以该特征在对应类别下为1的条件概率ng_prob *= self.ng_result[index][1] # 乘以 P(特征i=1|ng)ok_prob *= self.ok_result[index][1] # 乘以 P(特征i=1|ok)# 比较后验概率,取概率较大的类别作为预测结果if ng_prob > ok_prob:list_result.append(0) # 预测为类别0(ng)else:list_result.append(1) # 预测为类别1(ok)return list_resultif __name__ == '__main__':# 构造特征数据(3个特征,10个样本)# 每个特征都是二值特征(0或1)x1 = np.array([0, 0, 0, 0, 0, 1, 0, 0, 0, 1]).reshape(-1, 1) # 特征1x2 = np.array([0, 0, 0, 0, 1, 0, 1, 0, 1, 1]).reshape(-1, 1) # 特征2x3 = np.array([0, 0, 0, 1, 1, 0, 0, 1, 1, 1]).reshape(-1, 1) # 特征3x = np.c_[x1, x2, x3] # 合并为3列特征矩阵,形状为(10, 3)# 构造标签数据(10个样本的类别)# 0表示ng,1表示oky = np.array([0, 0, 0, 0, 0, 0, 0, 1, 1, 1]).reshape(-1, 1)# 打印特征和标签数据print("特征数据(10个样本,3个特征):")print(x)print("\n标签数据(0表示ng,1表示ok):")print(y)# 创建并训练模型bayes = BayesModel()bayes.fit(x, y)# 预测新样本new_samples = [[1, 1, 1], [0, 1, 1], [1, 1, 0]]predict_new = bayes.predict(new_samples)print("\n新样本的预测结果:", predict_new)# 预测训练集样本(查看模型对训练数据的拟合效果)predict_train = bayes.predict(x)print("训练集的预测结果:", predict_train)