【洛谷】单向链表、队列安排、约瑟夫问题(list相关算法题)

---

单向链表

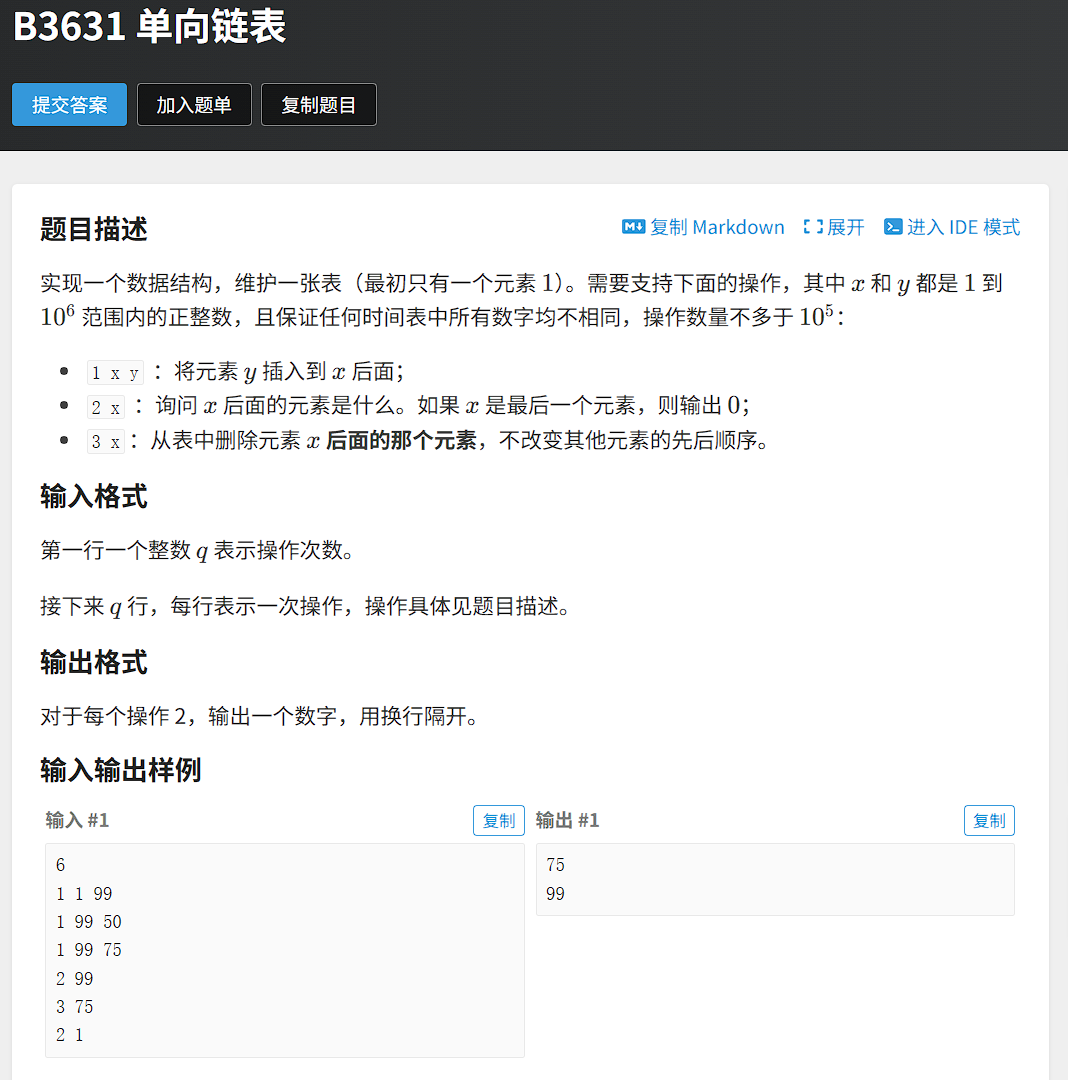
题目描述

题目解析

这道题因为有大量的任意位置插入删除，所以肯定不能用数组，用链表是最合适的，而在算法竞赛通常都用静态链表，所以这道题我们选用静态单链表。
这道题题目规定保证任何时间表中所有数字均不相同，所以我们可以用mp输入登记插入数据所在位置，高效率完成find操作。
三个操作每一个操作都需要先找到x的物理结构下标，所以我们先借助mp数组将x的下标存到p中，静态链表的插入删除操作小编专门出了一篇博客，感兴趣的读者可以移步：点击此处
需要注意的是首先删除操作时需要先将x在mp数组中删除再erase x，如果先erase x的话，后面删除x在mp数组的标记的操作就是删除的x的下一个结点在mp数组的标记了。然后题目规定一开始链表里除了哨兵位还有一个存1的结点。

代码

using namespace std;
#include <iostream>const int N = 1e6 + 10;  //单个数值的范围
const int M = 1e5 + 10;  //数量范围
int e[M], ne[M], mp[N],id, h;int main()
{id++;e[id] = 1;mp[1] = id;int q;cin >> q;int op, x, y;while (q--){cin >> op >> x;//p是x存的物理结构下标int p = mp[x];   if (op == 1){cin >> y;id++;e[id] = y;mp[y] = id;ne[id] = ne[p];ne[p] = id;}else if(op == 2){cout << e[ne[p]] << endl;}else{if (ne[p] != 0){mp[e[ne[p]]] = 0;ne[p] = ne[ne[p]];}}}return 0;
}

队列安排

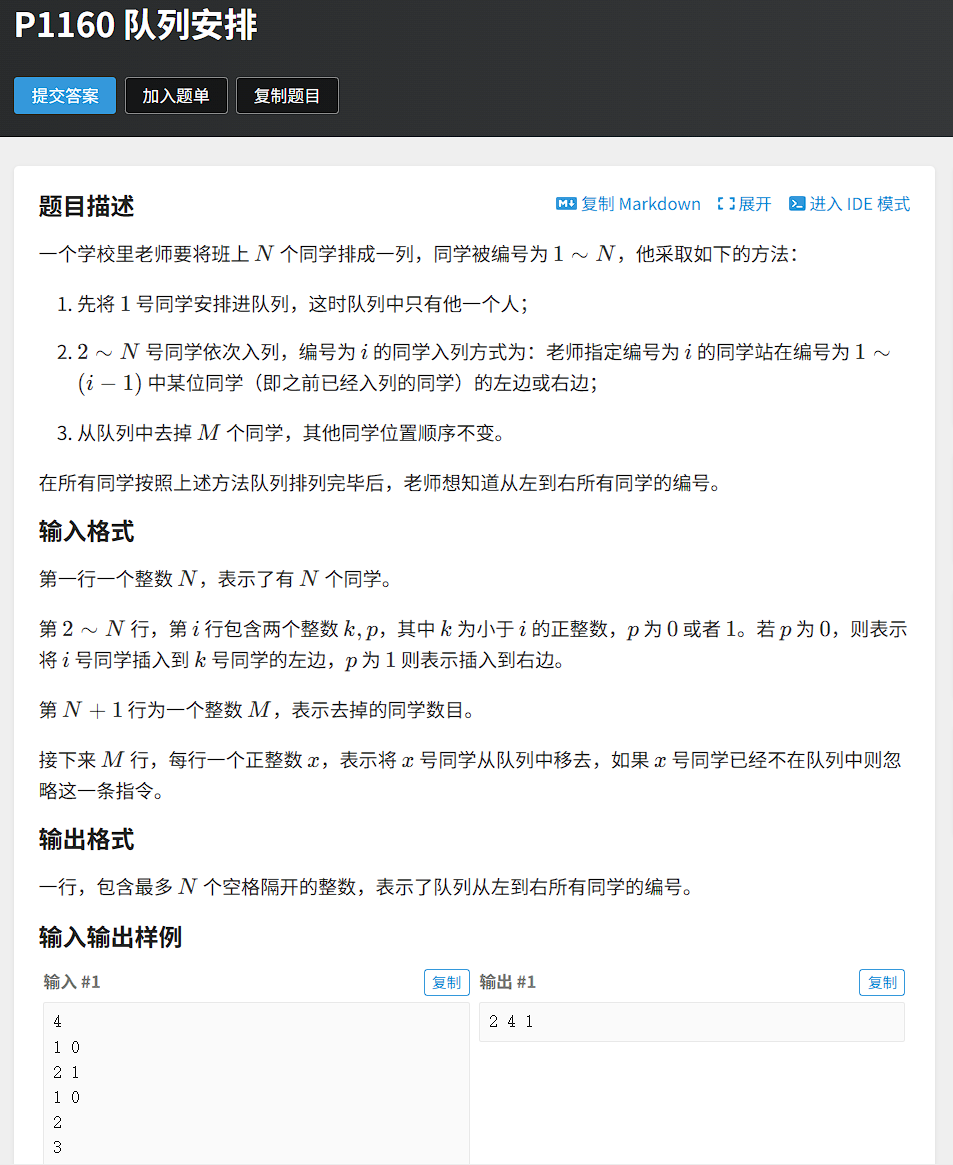
题目描述

题目解析

我们先分析一下，这道题有频繁的任意位置插入删除，不能用顺序表只能用链表，而且是在指定位置的前面或者后面插入删除，那么只能用双向链表。
这道题很特殊，因为它的按顺序插入的，所以它的插入的顺序就是数组的物理下标，也等于e[
]数组里的值，所以id就等于插入的顺序j，(有就是for循环里的j的值)我们要之前要借助mp[
]才能找到的插入位置的数组下标在这道题就等于k。删除时题目规定不能重复删，那创建一个数组st来标记某个物理下标是否被删除过，被删除过就置为true，若判断当前位置为true，直接continue跳过当次循环操作。
最后因为数组的物理下标直接等于e[ ]数组里的值，所以直接循环遍历打印数组的物理下标。

代码

using namespace std;
#include <iostream>const int Q = 1e5 + 10;
int ne[Q], pre[Q], h;
bool st[Q]; //用来标记x位置是否被删除int main()
{ne[1] = h;pre[1] = h;ne[h] = 1;pre[h] = 1;int N;cin >> N;//插入int k, p;for (int j = 2; j <= N; j++){cin >> k >> p;if (p == 0){ne[j] = k;pre[j] = pre[k];ne[pre[k]] = j;pre[k] = j;}else{ne[j] = ne[k];pre[j] = k;pre[ne[k]] = j;ne[k] = j;}}//删除  int M, x;cin >> M;while (M--){cin >> x;if (st[x] == true)continue;ne[pre[x]] = ne[x];pre[ne[x]] = pre[x];st[x] = true;}//输出  for (int i = ne[h]; i; i = ne[i]){cout << i << " ";}return 0;
}

约瑟夫问题

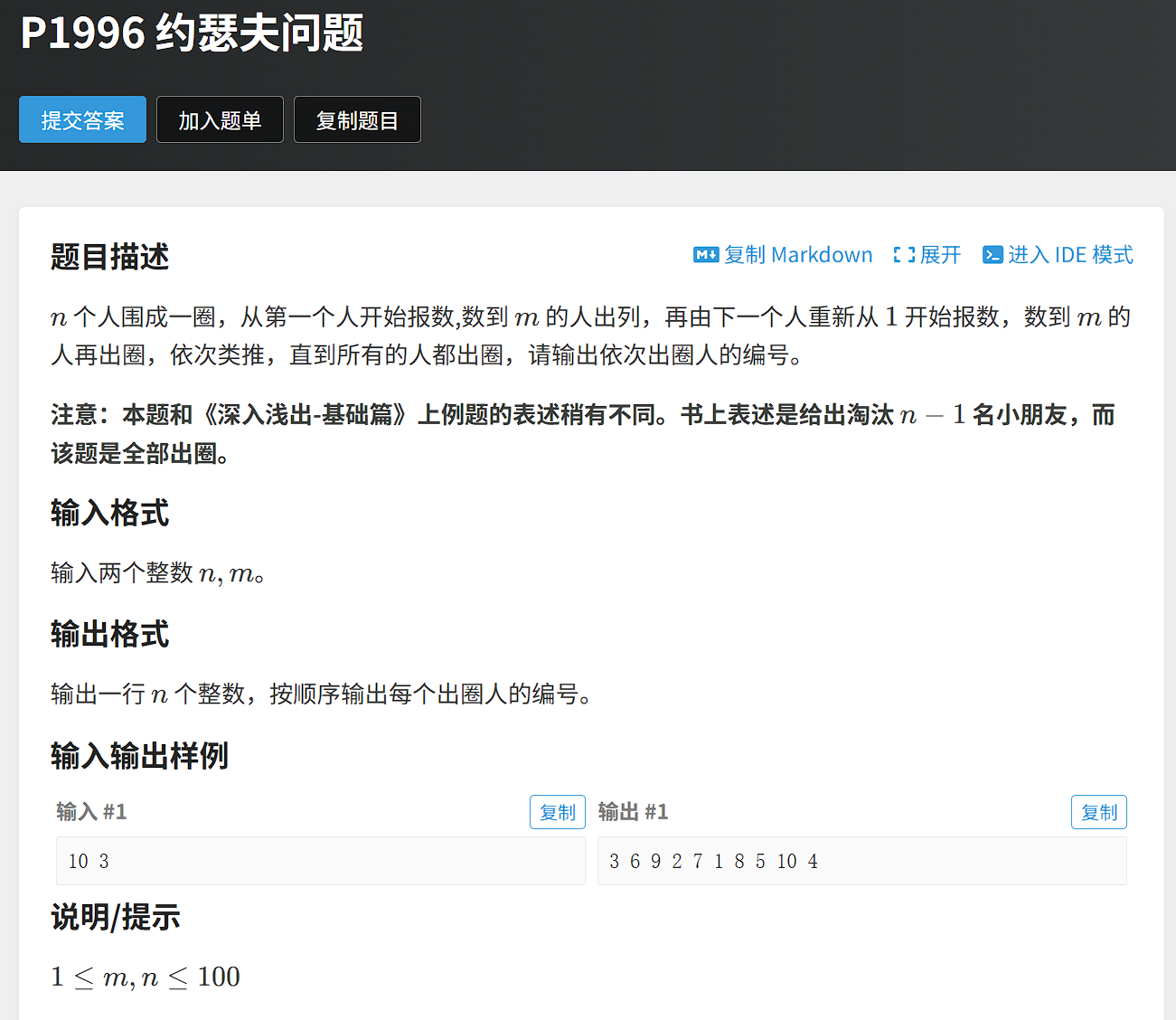
题目描述

题目解析

这道题思路很多，小编这里创建一个双向循环链表来解决，要注意根据题意我们要用循环链表来模拟一个圈，所以不能带哨兵位。
首先创建出一个n个结点的链表。然后从下标为0开始，每遍历m个结点就把当前结点打印出来，然后删除当前结点，指针再指向删除结点的下一个结点，最后把所有结点删除停止循环们也就是循环n次。

代码

using namespace std;
#include <iostream>const int N = 100 + 10;
int e[N], ne[N], pre[N], id, h;int main()
{int m, n;cin >> n >> m;//初始化e[0] = 1;ne[0] = 0;pre[0] = 0;for (int i = 1; i < n; i++){e[i] = i + 1;ne[i] = 0;pre[i] = i - 1;pre[h] = i;ne[i - 1] = i;}//循环打印删除int cur = 0;while (n--){int tmp = m;while (--tmp){cur = ne[cur];}cout << e[cur] << " ";//删除cur所在结点ne[pre[cur]] = ne[cur];pre[ne[cur]] = pre[cur];cur = ne[cur];}return 0;
}

以上就是小编分享的全部内容了，如果觉得不错还请留下免费的关注和收藏如果有建议欢迎通过评论区或私信留言，感谢您的大力支持。
一键三连好运连连哦~~