当前位置：首页 > news >正文

数据结构自学Day14 -- 归并排序

news 2025/7/26 13:55:21

一、归并排序的核心思想🧠

归并排序的核心思想就是：“将两个有序数组合并起来，合并后的数组就是有序的”，如果分开的序列不是有序的，则将原序列分解为更小的子序列来解决，然后将排好序的子数组合并起来。分而治之（Divide and Conquer）

📌 基本步骤：

分解（Divide）：

将数组从中间一分为二。
递归排序（Conquer）：
递归地对左右两个子数组排序。

合并（Combine）：
将两个已经排序好的子数组合并成一个有序数组。

二、归并排序的递归实现

假如序列可以被分解为两个有序序列，那么我们利用双指针遍历这两个序列，将元素按从下到大放到新数组中，这就是归并排序的思想，但是实际上我们的序列可能是无序的，没有办法划分成两个有序的序列，但是每个元素可以看成有序的，所以利用递归不断将序列划分，划分到子序列由单个元素组成，然后递归进行归并排序，放排序好的数据放到新数组中。

思维导图：

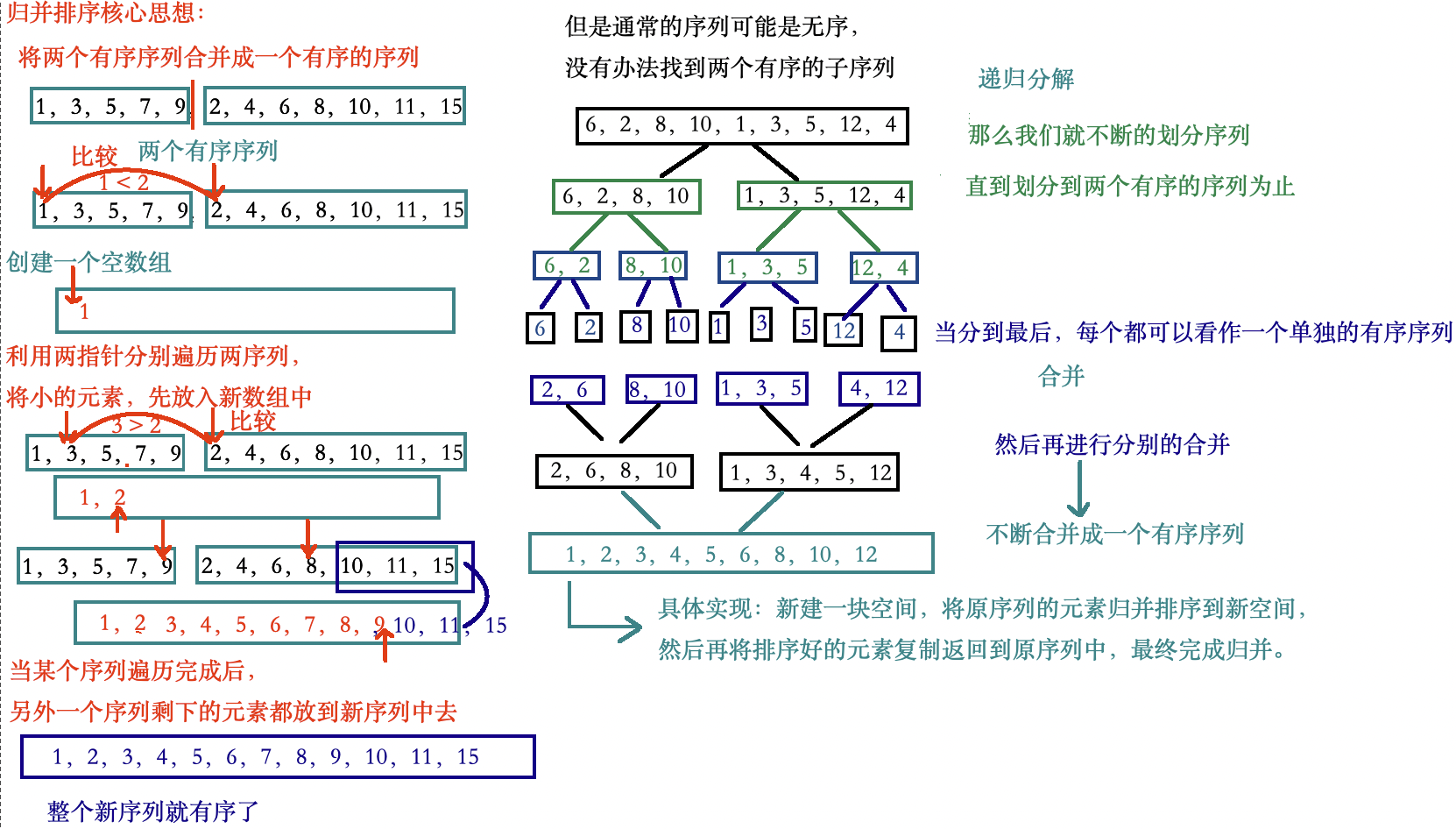
递归归并的代码实现

//递归分解归并函数
void _Merge_Sort(int*arr,int left,int right,int* tmp){assert(tmp);\if(left>=right){return;}int mid = (left+right)/2;int begin1= left; int end1 = mid;int begin2= mid+1; int end2 = right;int index = left;_Merge_Sort(arr,left,mid,tmp); //递归分解_Merge_Sort(arr,mid+1,right,tmp);//归并排序while (begin1 <= end1 && begin2 <= end2){    // 比较左右两个区间，谁小就放入 tempif(arr[begin1]<=arr[begin2]){tmp[index++] = arr[begin1++];}else{tmp[index++] = arr[begin2++];}}while (begin1 <= end1){tmp[index++] = arr[begin1++];}while (begin2 <= end2){tmp[index++] = arr[begin2++];}//把排好序的元素放回arrfor(int j =0;j<=right;j++){arr[j] = tmp[j];}
}void Merge_Sort(int* arr,int size){assert(arr);int* tmp = (int*)malloc(size*sizeof(int));int left = 0;int right = size-1;_Merge_Sort(arr,left,right,tmp);free(tmp);
}

三、非递归的归并排序实现

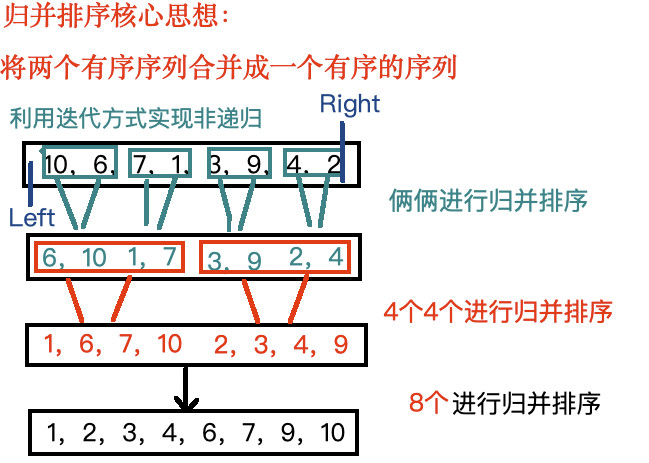
归并排序的迭代实现是从底向上的过程。它首先将整个数组看成由多个“长度为1”的有序子序列组成，然后不断两两合并相邻的子序列。每一轮合并后，子序列的长度翻倍：从1变为2，再到4，8，……直到整个数组有序。

例如：

第1轮：将相邻两个元素合并成长度为2的有序序列；gap = 1
第2轮：将相邻两个长度为2的序列合并为长度为4的有序序列；gap = 2
第3轮：将相邻两个长度为4的序列合并为长度为8的有序序列；gap = 4
以此类推，直到整个数组排好序。

这种实现方式避免了递归，适合用循环结构控制归并过程。

思维导图

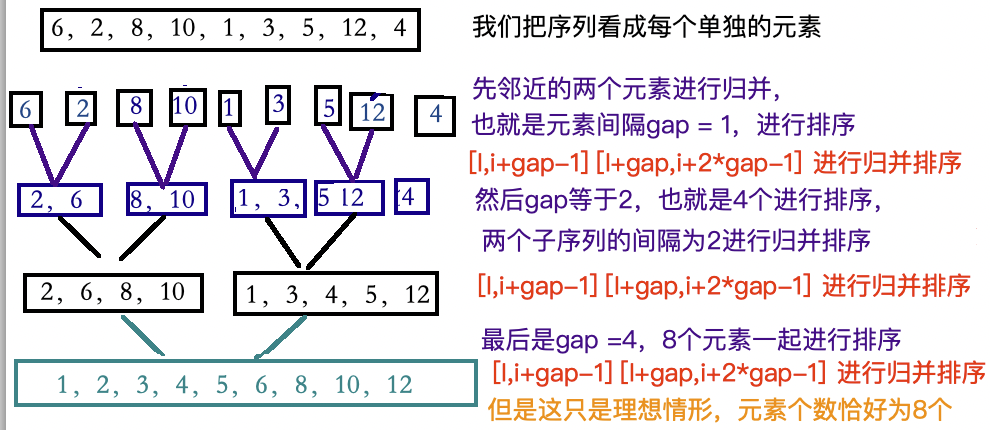
这是理想情形，我们的序列元素个数正好为2^n个，但是如果当我们的元素个数不再是2^n，比如我们的元素个数是12个，这就会导致划分序列时，可能无法划分成相同元素个数的两个子序列。当进行归并时，要注意边界的处理。举个例子：

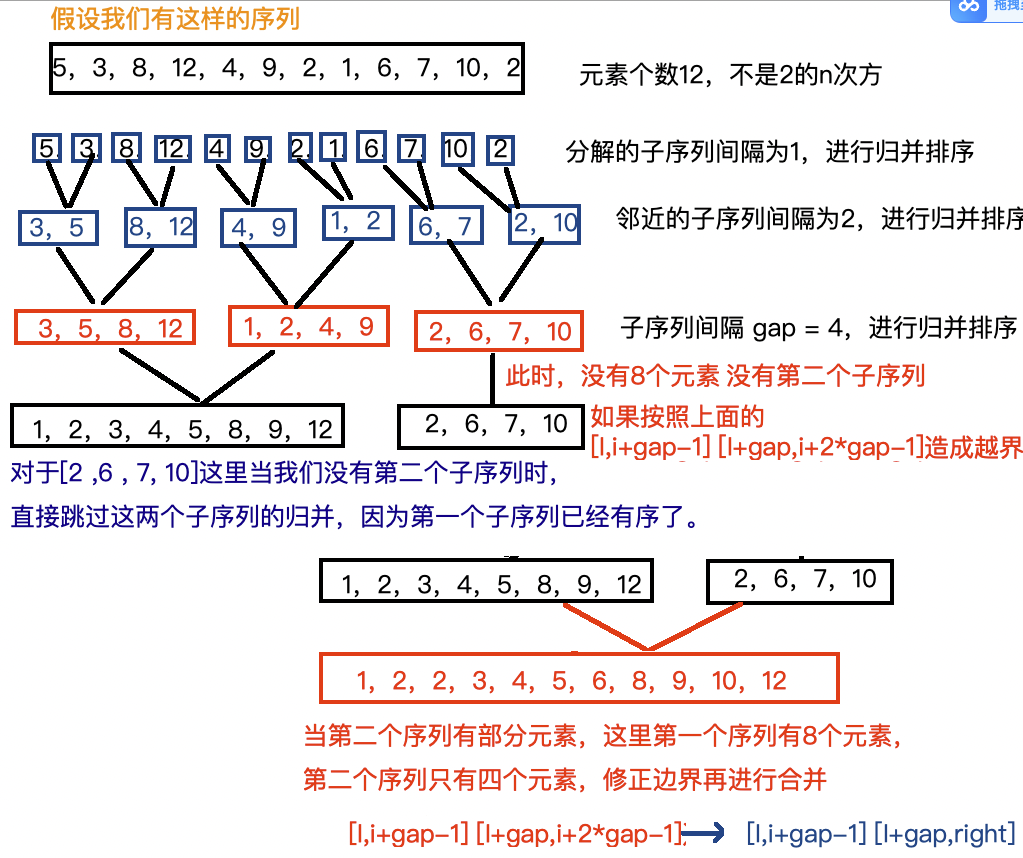
非递归归并排序的代码实现

//单躺归并
void Merge_arr(int*arr,int begin1,int end1,int begin2,int end2,int* tmp){int index = begin1; int left = begin1;int right = end2;while (begin1 <= end1 && begin2 <= end2){    if(arr[begin1]<=arr[begin2]){tmp[index++] = arr[begin1++];}else{tmp[index++] = arr[begin2++];}}while (begin1 <= end1){tmp[index++] = arr[begin1++];}while (begin2 <= end2){tmp[index++] = arr[begin2++];}//把排好序的元素放回arrfor(int j =left;j<=right;j++){arr[j] = tmp[j];}
}
// 迭代实现
void Merge_SortNonR(int* arr,int size){assert(arr);int* tmp = (int*)malloc(size*sizeof(int));int left = 0;int right = size-1;int gap = 1; // 迭代处理while (gap<size){for(int i = 0;i<=right;i+=2*gap){int begin1 = i;int end1 = i+gap-1;int begin2 = i+gap;int end2 = i+2*gap-1;//判断边界if(begin2>right){break;}if(end2>right){end2 = right;}//归并排序Merge_arr(arr,begin1,end1,begin2,end2,tmp);}gap*=2;}free(tmp);
}

四、时间与空间复杂度

项目	复杂度说明
最坏时间复杂度	O(n log n)
最好时间复杂度	O(n log n)
平均时间复杂度	O(n log n)
空间复杂度	O(n)（需要辅助数组）
稳定性	✅ 稳定排序

五、归并排序的优缺点总结

优点	说明
稳定性好	相同元素相对位置不变
时间复杂度稳定	O(n log n)，不管数据如何
适合链表	因为链表插入快，空间也不大
外部排序适用	可处理大数据（归并可分批处理）