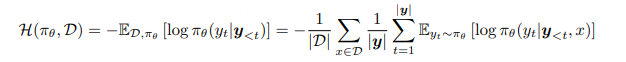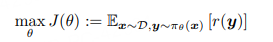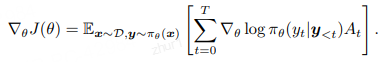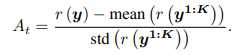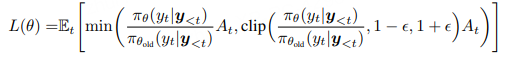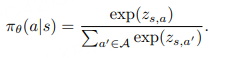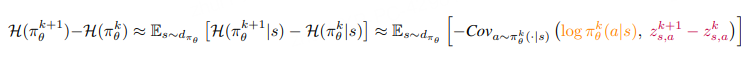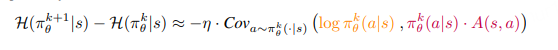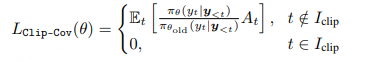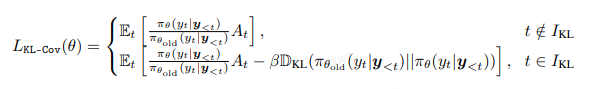强化学习之策略熵坍塌优化-clip conv kv conv

策略熵（Policy entropy）。

策略熵用于衡量智能体所选动作的可预测性或内在随机性。给定策略模型 πθ 和训练数据集 D，我们通过计算模型在训练数据上的平均 token 级熵来度量策略熵，其定义如下：

该熵值量化了策略对当前提示的不确定性水平，并被广泛用作最大熵强化学习中的正则化项（Ziebart et al., 2008；Haarnoja et al., 2017, 2018）。在实际操作中，我们对从训练数据中随机采样的每一批提示计算其熵值。

二 clip-cov: 控制策略熵

The Entropy Mechanism of Reinforcement Learning for Reasoning Language Models

2.1 策略熵的坍缩

本文研究LLM RL训练的重要问题：策略熵的崩塌。
这种现象在大规模RL训练中经常出现，若不引入熵的调控，策略熵会在训练初期迅速下降，导致模型过度自信，探索能力减弱，策略性能饱和。

本文建立了一个熵与模型性能之间的转换公式，表明策略性能是以策略熵为代价换来的，熵的耗尽会成为性能提升的瓶颈，并且可以根据熵来预测RL训练出的模型能力的上限。
本文的推导指出：策略熵的变化是由动作概率与logits变化之间的协方差驱动的，实验表明，协方差项的数值变化与熵的变化几乎完全匹配。

本文进一步提出了控制策略熵的方法，限制高协方差token的更新，
包括Clip-Cov方法：对高协方差token的梯度进行裁剪；随机选取少量协方差为正的 token 并切断其梯度；
以及KL-Cov方法：对高协方差token引入KL惩罚。对协方差最大的 token 施加 KL 惩罚。
实验结果表明，这些方法鼓励了探索行为，从而有助于策略避免熵崩塌，提升模型的性能。

2.1.1 策略熵为什么重要

强化学习的核心难题在于利用–探索权衡（Sutton, 1988）：在复用已被验证的策略与搜寻全新策略之间取得平衡。
就探索而言，一个关键概念是策略熵，它衡量策略在选择动作时的不确定性。
在 RL 文献中，抑制策略熵下降被视为多数算法的必要条件，并通过正则化手段对策略熵进行积极引导与主动控制。

2.1.2 策略熵坍缩很常见，且与性能提升密不可分

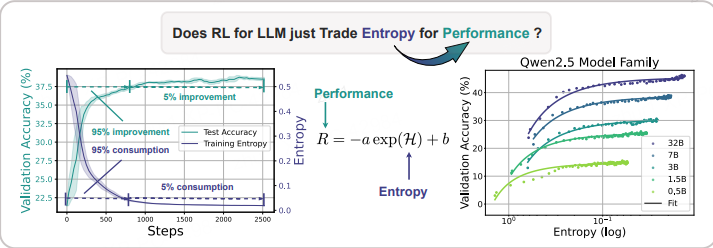
图 1 左：熵坍缩与性能饱和。超过 95% 的熵下降 / 性能提升发生在 RL 训练早期。随后模型进入平台期，几乎不再提升。
右：验证性能与策略熵之间的可预测关系。在无干预情况下，策略以指数方式“拿熵换性能”，出现清晰可见的上限，阻碍进一步改进。

总结公式：R = −a exp(H) + b

• 与 Scaling Law类似，利用–探索曲线在给定策略模型与训练数据后即被预先决定。这使我们可以在 RL 早期阶段就预测策略性能，并借助小模型预测大模型性能
• 更重要的是，该方程表明策略性能的上限也是确定的：当策略熵耗尽（H = 0）时，R = −a + b，因此继续扩大 RL 训练算力的边际收益可能极低。更糟糕的是，朴素地使用熵正则化方法已被证明无效（第 4.1 节）。简言之，严重制约了 LLM 推理任务中 RL 的可扩展性。
  系数 a、b 反映了策略与数据的内在特征；

2.1.3 熵–与高协方差的关系，引入新方法

从理论与实验两方面分析了熵的动态。
关键发现是：

• 对 LLM 这类 softmax 策略而言，相邻两步之间的熵变正比于某动作的 log-probability 与对应 logit 变化之间的协方差（Liu, 2025）。
• 进一步地，在策略梯度或自然策略梯度类算法下，logit 差正比于动作优势值。
• 直观上，高优势且高概率的动作会降低策略熵，而高优势但低概率的动作会提升熵。这一理论结论被实验结果验证。

训练早期，策略在训练数据上呈现高协方差，表明模型信心校准良好（Kadavath et al., 2022），因此可以安全地利用高置信轨迹，强化信念并最小化熵（Zuo et al., 2025; Zhang et al., 2025; Agarwal et al., 2025）。随着训练进行，协方差逐渐下降但仍保持正值，持续将策略熵拉低。

对熵动力学的分析显示，高协方差对可扩展 RL 有害，
从而为我们提升策略熵提供了明确指引：限制高协方差 token 的更新步长。
由此，我们提出两种对应的熵控制策略——Clip-Cov 与 KL-Cov，分别替代代理损失中的裁剪与 PPO-KL 方法（Schulman et al., 2017b）。
实验表明，通过调节阈值参数，我们可以主动控制策略熵，使模型摆脱低熵陷阱，在数学推理任务上取得更优性能。

2.2 历史方法

在可验证的数学推理代码等任务上，通常会用RL微调LLM，优化目标为最大化reward：

最简单的求解方法是policy gradient策略梯度算法，例如reinforce算法：

其中 A_t 表示当前动作的优势（advantage），在不同 RL 算法中有不同的实现方式。

REINFORCE（Williams, 1992）直接将优势定义为A_t = r(y)。

为降低方差，GRPO与 RLOO（Kool et al., 2019; Ahmadian et al., 2024）进一步引入了按组归一化。以 GRPO 为例，它对每个提示采样 K 条完整回答，并按如下方式估计优势：

为了处理 off-policy 数据并限制策略更新幅度，PPO（Schulman et al., 2017b）提出clip优化如下的替代目标函数：

RLOO算法通过减掉reward多次采样的均值来降低方差,对于同一 prompt 在线采样k次，取除自己外的其他
k-1条回答的平均 reward 作为 baseline：

RL的训练过程往往需要关注策略熵，熵越大，模型的探索能力越强。RL训练过程中entropy通常会下降，因此会加入entropy loss来控制策略熵的降低。
但是这类entropy loss的方法效果有限

2.3 观察实验设置

本文选取了Qwen，Mistral，Llama等多个模型，
训练数学和代码数据，
在MATH500，AIME2024，AMC，OlympiadBench，OMNI-MATH， Eurus-2-RL-Code，KodCode等benchmark上进行测试。

• 从零开始：采用 “Zero” 设定（DeepSeek-AI et al., 2025），基于 veRL 框架（Sheng et al., 2024）从基础模型启动 RL。
• 算法：GRPO（Shao et al., 2024）、REINFORCE++（Hu, 2025）、PRIME（Cui et al., 2025）。
• 超参数：
  – 策略模型学习率 5 × 10⁻⁷；PRIME 中的隐式 PRM 学习率 10⁻⁶（Yuan et al., 2025）。
  – 策略与 PRM 的 batch size 均为 256，micro-batch size 为 128。
  – rollout 阶段采集 512 条提示，每条提示采样 8 条回答。
  – 默认参考 KL 散度系数设为 0。
  – 策略损失的 ϵ（公式 4）取 0.2。
• 数据过滤：剔除那些收到全部正确或全部错误回答的提示。

2.3.1 entropy loss与性能

实验结果表明，entropy的下降和性能的提升呈正相关的关系：高度一致的模式

展示了 11 个模型在 2400 个梯度步 RL 训练过程中，熵消耗与性能提升的平均归一化百分比。可以看到：
• 前 200 个梯度步（仅占全程 1/12）就消耗了 73% 的熵并带来了 76% 的性能提升；
• 前 800 个梯度步（占全程 1/3）已累计贡献 94% 的熵损失与 93% 的性能增益。
这意味着剩下 2/3 以上的训练步只带来边际收益。

2.3.2 可以高度拟合,两个系数即可

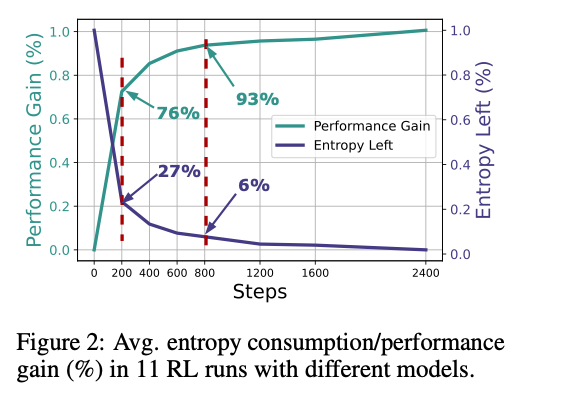
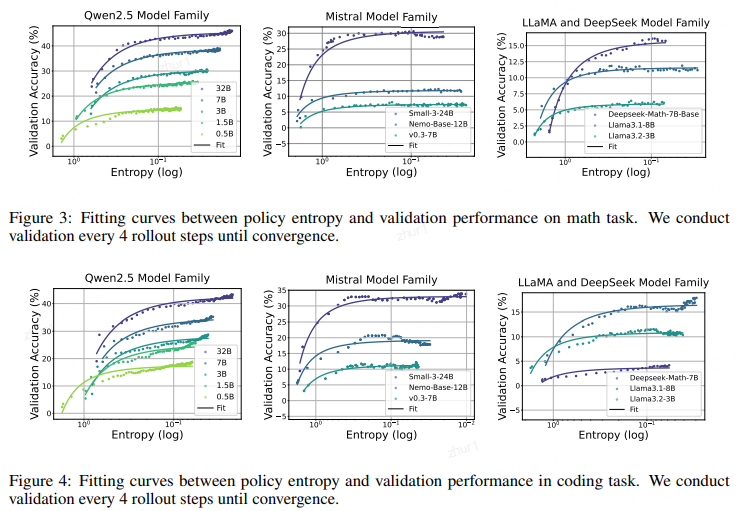
用 R 表示验证性能、H 表示熵，我们发现两者可以用指数关系精确拟合
拟合结果
仅用两个系数即可对 200 多个数据点进行拟合，显示出极高的规律性和一致性。

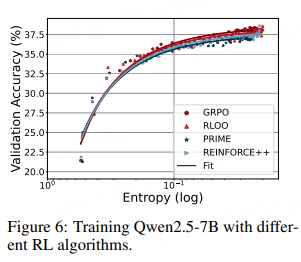
2.6.3 系数与算法无关

我们考察了不同 RL 算法是否会影响拟合函数。图 6 分别给出了 GRPO、RLOO 与 PRIME 的拟合曲线。尽管这三种优势估计方法各异，它们得到的熵–性能函数几乎重合，表明系数 a、b 刻画的是策略模型与训练数据的内在属性，而非算法细节。

2.6.4 利用系数预测参数放大后的表现

进一步观察 a、b 的含义：
• 对 R = −a e^H+ b 求导得 dR/dH = −a e^H，因此 a 表示“每单位熵能换取多少性能”的转换效率；
• −a + b 即熵完全耗尽（H = 0）时的验证分数，是模型在给定数据上的性能上限。

直观上，a、b 应与模型规模相关：更大的模型通常能更高效地用熵换奖励，也能获得更高的极限性能。为此，我们选取架构相同、训练流程一致的 Qwen2.5 家族进行验证。

图 7 绘制了模型参数量（不含嵌入层）与 a、b 的关系。可以看到，在数学与编程任务上，a、b 均随模型规模呈平滑的对数–线性变化。这种 log-linear 规律也在 Gao et al. (2022) 中被观察到。因此，只需用小模型跑完训练并记录 a、b，即可外推同家族大模型的系数，从而无需真正训练大模型就能预测其最终 RL 性能。图 13 进一步表明，系数还与训练数据有关。

2.4 策略熵的动力学分析

2.4.1 核心结论

(1) 对于包括 LLM 在内的 softmax 策略，策略熵的变化由动作 log-probability 与其 logits 变化的协方差决定。
(2) 在策略梯度（Policy Gradient）和自然策略梯度（Natural Policy Gradient）下，logits 的变化正比于动作优势（advantage），因此高协方差将导致策略熵迅速下降——这正是我们在 LLM 推理 RL 中观测到的熵坍缩现象。

我们已经揭示，熵坍缩问题将严重阻碍 LLM 推理任务的 RL 规模扩展。为破解这一难题，需要对策略熵的动力学建立更系统的理解：熵何时下降，何时上升。本节聚焦“步级”熵差 H(π^{k+1}_θ) − H(π^k_θ)。首先从理论出发，4.2 节推导 softmax 策略熵的一阶微分；4.3 节进一步推广到策略梯度与自然策略梯度算法；4.4 节用实验验证结论。

2.4.2 softmax 策略的熵动力学

在第 k 步，我们希望计算一次参数更新前后的熵差，即 H(π^{k+1}_θ) 与 H(π^k_θ)

softmax形式定义

其中 s ∼ d^{π_θ} 和 a ∼ π^k_θ(·|s) 分别表示状态与动作的采样，z_{s,a} 是给定状态 s 下动作 a 的 logit 输出。对于任意 softmax 策略，我们有如下引理：
引理 1（softmax 策略的熵差）（证明见附录 E.2，改编自 Liu, 2025）
假设策略 π_θ 是一个表格形式的 softmax 策略，每个状态-动作对 (s, a) 对应一个独立的 logit 参数 z_{s,a} = θ_{s,a}，则在一步更新后，给定状态 s 的策略熵差在一阶近似下满足：

该引理表明，策略熵的变化近似等于动作 log-probability 与 logit 变化之间的负协方差。换言之，若某个动作 a 在更新前被策略赋予高概率，且其对应 logit 在更新后又上升，那么它将导致策略熵下降。

2.4.3 策略梯度 / 自然策略梯度下的熵动力学

由引理 1 可知，logit 的步级变化 z^{k+1}{s,a} − z^k{s,a} 决定了熵变，而这一变化又依赖于具体算法。
下面我们进一步推导在策略梯度（Williams, 1992）和自然策略梯度（Kakade, 2001）下的 logit 变化。

假设我们使用策略梯度更新 actor 策略，则有
z^{k+1}{s,a} − z^k{s,a} = −η · ∇_z J(θ)，
其中 J(θ) 是目标函数，η 是学习率。
根据式 (2) 计算 ∇_z J(θ)，我们得到如下命题：
命题 1（vanilla 策略梯度下的 logit 差）（证明见附录 E.3）
若 actor 策略 π_θ 为表格 softmax 策略，且按式 (2) 以学习率 η 做梯度回传更新，则两步之间的 logit 差满足：

2.4.4 实验分析

我们使用 GRPO 并在纯策略梯度（on-policy，无 PPO 代理损失）方式下训练 Qwen2.5-7B。
采用 bandit 设定：提示 x 视为状态，整条回复 y 视为动作。
此时协方差项简化为
Cov_{y∼π_θ(·|x)} [log π_θ(y|x), A(y)]。

训练期间，我们对每个 prompt 计算组内协方差并在批次内取平均，同时对 log-prob 按回复长度归一化。

实验结果
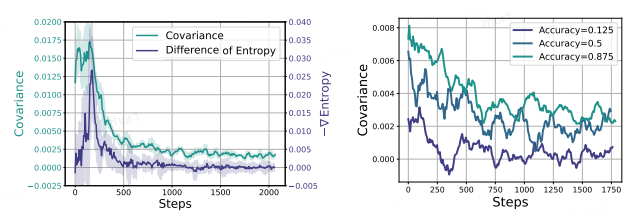
记录两个关键指标：协方差 Cov(·) 与步级熵差−dH(π_θ)，并分析其关系与动态：

Cov(·) 与 −dH 的动态一致性
定理 1 指出 −dH ∝ Cov(·)。
图 8 左显示，二者曲线高度重合，为定理提供了强有力实证。训练早期熵迅速下降，Cov(·) 保持较大正值；随着训练推进，熵降趋缓，Cov(·) 亦降至较低水平，反映策略逐渐收敛。整个过程中 Cov(·) 始终为正，导致熵持续下降。

不同难度样本的 Cov(·) 差异
利用组采样策略，我们按准确率将样本分为易、中、难三组。图 8 右显示：
• 难度越高（准确率越低）的样本，Cov(·) 幅度越小；
• 难度越低（准确率越高）的样本，Cov(·) 幅度越大。
这与直觉相符：模型在易样本上更自信且校准更好，高概率动作与优势估计高度对齐；在难样本上学习困难，高概率动作并不总伴随更高回报，故协方差减小。

2.5 通过协方差正则化实现熵控制

核心结论
限制高协方差 token 的更新幅度即可有效控制策略熵。我们提出了两种简单却高效的方法：
• Clip-Cov：随机裁剪少量高协方差 token 的梯度；
• KL-Cov：对高协方差 token 施加 KL 惩罚。
二者都能阻止熵坍缩、促进探索，并在下游任务上取得更好性能。

2.5.1 熵正则化的局限性

传统 RL 常用熵损失（entropy loss）或参考 KL 惩罚来控制熵。我们在 LLM 上的实验表明：
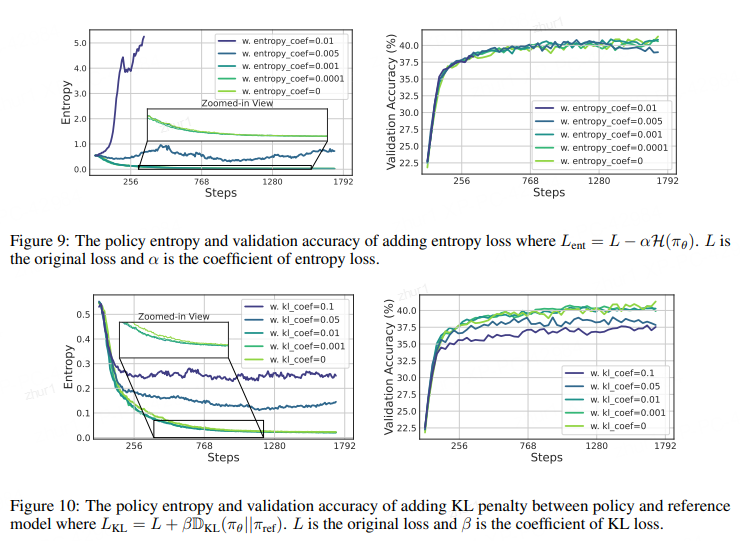
• 熵损失对系数极度敏感：小系数（0.0001, 0.001）几乎无效；大系数（0.01）导致熵爆炸；即使 0.005 能稳定熵，也无法超越基线（图 9）。
• 参考 KL 虽能稳住熵，却带来性能下降（图 10）。
综上，简单沿用传统熵正则化在 LLM 上不仅超参敏感，还可能损害性能，因此近期工作普遍舍弃它们（Cui et al., 2025; Hu et al., 2025; Liu et al., 2025; Yu et al., 2025）。

这里可以认为性能是由entropy转换带来的，模型起始entropy越大，最终RL训练出的模型能力越强。
本文提出了entropy和模型性能之间存在下列公式：
同时，当entropy=0时，可以计算出性能的上界。

2.5.2 基于协方差的控制方法

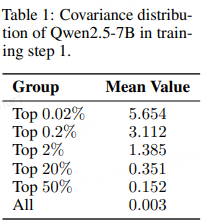
既然熵动力学与“动作概率 × 优势”的协方差紧密相关，而表 1 显示极少量 token 的协方差远大于均值，正是这些“离群” token 主导了熵坍缩。

因此，我们借鉴 PPO 的裁剪/ KL 约束思想，提出两种“协方差感知”方法：

• 定义
  对一批 N 个 rollout token，
  记 πθ(y_i) 为第 i 个 token 在给定前缀下的输出概率。
  根据定理 2，先定义 token-wise 中心化交叉积：
  Cov_i = (log πθ(y_i) − μ_log)(A(y_i) − μ_A)
  其中 μ_log、μ_A 为批次均值；Cov_i 的期望即定理 2 中的协方差。

Clip-Cov
计算 Cov_i 后，随机选取比例 r·N 的高协方差 token（Cov_i 最大的一批），将它们从策略梯度中“梯度断流”：若 token i 被选中，则 ∇_θ log πθ(y_i) 不再回传。
其中 I 表示被选中的 token 索引集合，r 为裁剪比例；ω_low、ω_high 是两个预设的协方差阈值，远高于平均协方差（>500 倍）。最终，凡索引落入 I 的 token，其梯度将被断开
其中 t 表示一条 rollout 响应中的第 t 个 token，每个 t 在全局批次 N 中都有唯一索引 i。

KL-Cov
KL-Cov 策略更为简洁。首先，与 Clip-Cov 一样计算每个 token 的协方差 Cov_i；随后对所有 token 按 Cov_i 降序排序，选出前 k 比例的 token（k ≪ 1）。最后，仅对这些选中的 token 施加 KL 惩罚（当前策略与 rollout 策略之间的 KL 散度）。此时的策略损失为：

其中 β 为 KL 惩罚权重系数。完整伪代码见 Listing 1。

2.5.3 实验设置

我们在数学任务上训练 Qwen2.5 系列模型，以验证 Clip-Cov 与 KL-Cov 的有效性。
训练数据使用 DAPOMATH（Yu et al., 2025）。
• 每个 rollout 步：对 256 条提示用温度 1.0 各采样 8 条回答，随后执行 8 次策略更新。
• 过滤掉“全对 / 全错”提示。

测试集：MATH500、AIME 2024/2025、AMC、OMNI-MATH、OlympiadBench、Minerva。评估时 AIME、AMC 温度 0.6，其余贪心解码。

基线与超参
• 基线：原始 GRPO；GRPO-Clip-higher（PPO 上阈值 ϵ 调为 0.28，Yu et al., 2025）。
• Clip-Cov：裁剪比例 r = 2×10⁻⁴，阈值 ω_low = 1，ω_high = 5。
• KL-Cov：比例 k = 2×10⁻³（7B）/ 2×10⁻⁴（32B），KL 系数 β = 1。
• 最大生成长度 8192。

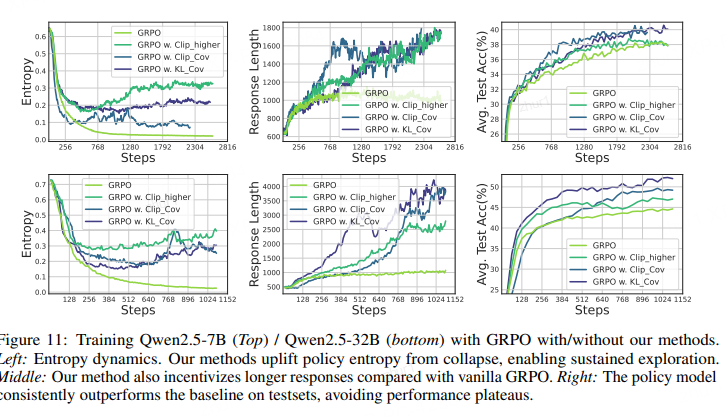
训练全程，KL-Cov 的熵始终保持在基线 10× 以上；基线熵率先触顶后停滞，而 KL-Cov 仍能继续下降并带来性能增长。
• 模型响应长度随训练稳步增加，验证集性能持续超越基线，说明方法在训练中持续“自由”探索，学到更优策略。
• 与 Clip-higher 相比，后者虽能在早期提升熵与性能，但后续逐渐不稳定，性能先饱和后下降；而本方法熵曲线更稳，最终显著优于基线。