当前位置：首页 > news >正文

基于位移传感器的转子质心角度位置检测：原理分析与实现

news 2025/7/26 9:31:43

针对旋转机械动平衡检测需求，本文提出一种基于双位移传感器的转子质心角度位置检测方案。通过正交信号解调与相位提取技术，实现高精度角度定位。

一、检测原理与系统设计

转子在旋转过程中因质量不平衡产生的离心力可表示为：

其中 m 为质量， $\omega$ 为角速度， $r$ 为偏心距， $\phi$ 为质心角度位置。

检测系统组成：

两个正交安装的位移传感器（X/Y方向）
信号调理电路
数字信号处理器
角度解算算法

传感器检测到的振动位移信号为：

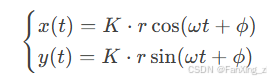
其中 K为系统增益系数。

二、复频域传递函数建模

信号处理流程的复频域模型如下：

[H(s)]          [H(s)]
x(t) ---->|----|--->I分支-------> arctan2(Q, I) ---> φ| × |                /
y(t) ---->|----|--->Q分支------/[正交解调]

其中核心环节为抗混叠滤波器和低通滤波器组成的复合传递函数：

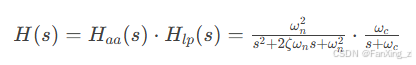
参数说明：

$\zeta$ ：阻尼比（取0.707）
$\omega_n$ ：固有频率（200 rad/s）
$\omega_c$ ：截止频率（100 rad/s）

三、MATLAB仿真实现

% 系统参数设置
zeta = 0.707;       % 阻尼比
wn = 200;           % 固有频率 (rad/s)
wc = 100;           % 截止频率 (rad/s)% 构建传递函数
num_aa = [wn^2];                    % 抗混叠滤波器分子
den_aa = [1, 2*zeta*wn, wn^2];      % 抗混叠滤波器分母
num_lp = [wc];                      % 低通滤波器分子
den_lp = [1, wc];                   % 低通滤波器分母% 系统串联
sys_aa = tf(num_aa, den_aa);        % 抗混叠滤波器模型
sys_lp = tf(num_lp, den_lp);        % 低通滤波器模型
sys_total = series(sys_aa, sys_lp); % 总传递函数% 绘制伯德图
figure('Color', 'white', 'Position', [100, 100, 800, 600])
bodeplot(sys_total, {1,1000});
grid on;
title('系统传递函数伯德图', 'FontSize', 14, 'FontWeight', 'bold');
set(findall(gcf, 'Type', 'line'), 'LineWidth', 1.5);

四、仿真结果分析

频率特性分析：

幅频特性
- 通带范围：1-100 rad/s（-3dB点）
- 阻带衰减：>40dB/dec
- 谐振峰值：<3dB（因ζ=0.707）
相频特性
- 通带相位延迟：<90°
- 相位线性度：在通带内保持良好

五、工程应用要点

传感器安装：
- X/Y传感器正交误差 <0.5°
- 安装距离控制在探头线性区内
实时处理算法：

// 伪代码实现
float calculate_phase(float x, float y) {static float I_prev = 0, Q_prev = 0;const float alpha = 0.02;  // 滤波系数// 正交解调float I = alpha * x + (1-alpha) * I_prev;float Q = alpha * y + (1-alpha) * Q_prev;// 更新历史值I_prev = I;Q_prev = Q;// 相位计算return atan2f(Q, I);  // 四象限反正切
}

3. 误差补偿策略：