【论文阅读50】-融合领域知识与可解释深度学习

这篇论文提出了一种融合领域知识与可解释深度学习的新方法，用于滑坡形变的时空预测。论文的核心内容和贡献包括：

1. 创新方法设计
   结合多监测点的滑坡形变数据和区域地质、环境等先验知识，利用自解释的深度学习模型（基于Transformer和LSTM架构），捕捉滑坡在空间和时间上的复杂动态关联，实现更准确的形变预测。

2. 解释性与物理一致性
   该方法不仅提升了预测准确度，还通过注意力机制和特征重要性分析，揭示了影响滑坡变形的关键因素和时空演化模式，使模型具有较好的可解释性和物理合理性。

3. 案例验证
   在黄连树水库滑坡和青藏高原白格滑坡两个典型案例中，方法成功识别了水位、降雨、温度等主要驱动因子，展现出对不同滑坡区域异质性响应的有效捕捉能力，并预测出了未来形变的趋势和不确定性。

4. 应用意义和未来展望
   该研究为滑坡监测预警提供了一种结合数据驱动与知识驱动的综合框架，增强了滑坡灾害预测的可靠性和解释力。论文还指出方法的局限性并提出了未来结合物理模型、多源数据和扩展至地震诱发滑坡等方向的发展前景。

总体来说，论文围绕“如何利用多源数据和领域知识，基于可解释深度学习模型，实现滑坡形变的精准预测与原因解析”展开，推进了滑坡灾害风险预警技术的发展。

[1] Ma Z, Mei G. Forecasting landslide deformation by integrating domain knowledge into interpretable deep learning considering spatiotemporal correlations[J]. Journal of Rock Mechanics and Geotechnical Engineering, 2025, 17(2): 960-982.

作者：
马正靖，梅刚*（通讯作者）

单位：
中国地质大学（北京），工程与技术学院，北京市 100083

文章历史：

• 收稿日期：2023年10月29日
• 修回日期：2023年12月29日
• 接收日期：2024年2月29日
• 在线发布日期：2024年6月4日

摘要：

由于多种内在与外在因素共同影响滑坡的系统性与局部异质性，其变形预测面临诸多挑战。尽管深度学习在提升滑坡可预测性方面具有潜力，但目前对于与滑坡相关的复杂变形模式仍缺乏充分探索，且深度学习模型本身存在不可解释性问题。

本文提出了一种融合领域知识、考虑滑坡变形时空相关性的整体性预测方法，构建了可解释深度学习模型。该方法通过在空间上捕捉不同观测点间多源变形数据之间的相互关联，提升了对滑坡系统性行为的理解与预测能力。同时，结合与各观测点相关的特定领域知识，将滑坡体的内在属性与外部影响变量进行融合，从而在方法中引入了局部异质性的考量，实现对不同滑坡区域中变形时序模式的识别。

通过水库诱发滑坡与蠕滑型滑坡的案例研究，表明该方法：（1）提高了滑坡变形预测的精度；（2）识别出重要的影响因子及其对时空变形特征的贡献；（3）揭示了识别这些因素与模式在滑坡预测中的重要作用。

本研究为深入理解与预测复杂滑坡行为提供了一条具有应用前景与现实意义的路径。

关键词： 地质灾害；滑坡变形预测；滑坡可预测性；融合知识的深度学习；可解释机器学习；注意力机制；Transformer

1. 引言

滑坡是一种常见的全球性自然灾害，已造成大量经济损失和人员伤亡（Petley, 2012；Froude 和 Petley, 2018）。滑坡往往还伴随次生灾害，如堰塞湖形成和洪水等，进一步加剧受灾地区的脆弱性（Fan 等, 2019a；Yang 等, 2022）。随着城市化加剧以及气候变化带来的风险，滑坡灾害防控显得尤为重要（Patton 等, 2019；Dille 等, 2022）。为了减轻滑坡对经济、公共安全和生态系统的影响，亟需设计并实施高效的预警系统（Gariano 和 Guzzetti, 2016；Piciullo 等, 2018），而这依赖于对滑坡的预测能力（包括预报、预测和预判）的提升（Guzzetti, 2021）。

滑坡预测需要对其时空特征有全面的理解。空间预测侧重于易发性分析，通过地形和环境条件评估滑坡发生的可能性（Reichenbach 等, 2018）；而本研究主要关注滑坡的时间预测，这对于滑坡预警系统至关重要。通过识别滑坡即将发生前的前兆，如地表变形加剧、降雨等，可实现滑坡的时间预测（Intrieri 等, 2019；Coppola 等, 2022）。

研究表明，不同类型滑坡具有不同的运动特征，这些特征受到内在与外在因素的共同影响（Guzzetti 等, 2008；Hungr 等, 2014；Kargel 等, 2016；Lacroix 等, 2022）。外在因素包括降雨模式、气候变化和人类活动；内在因素则指滑坡物质的地质与岩土力学性质，如土壤成分和岩体结构。例如，水库滑坡的变形通常受水位波动或暴雨控制，常呈现出阶跃状和周期性震荡的特征（Yao 等, 2019；Zou 等, 2023）；而蠕滑型滑坡通常出现在高海拔地区，变形过程缓慢，受到如降雨、融雪引起的温湿度变化等复杂水文过程的影响。

在外因持续施加和内因不断演变的共同作用下，滑坡变形可能最终发展为突然的灾难性破坏。在这一过程中，滑坡变形监测成为关键的运动学参数（Frattini 等, 2018；Hu 等, 2020, 2021；Zeng 等, 2023）。滑坡在破坏前通常会经历可识别的位移演化过程，主要表现为三阶段变形模式：初始阶段应变速率降低，次稳态阶段应变速率稳定，最后加速阶段导致破坏。因此，滑坡位移直接反映滑体稳定性，是最可靠、最常用的滑坡预测参数。

在不同阶段及其内外因影响下，尽早识别关键变形模式对于预测滑坡破坏至关重要，并可纳入预警系统以避免灾难性后果。近年来，随着高分辨率监测技术的进步，尤其是在变形监测方面，滑坡行为的实时测量能力显著提升（Intrieri 等, 2017；Bru 等, 2018；Zhou 等, 2022；Casagli 等, 2023）。这促进了滑坡前兆识别与变形预测研究的快速发展。

通过分析多种监测手段获得的变形数据，研究者能够识别滑坡行为中的模式和趋势，进而发展出精密的数据驱动预测模型（Bekaert 等, 2020；Wasowski 和 Pisano, 2020；Cascini 等, 2022；Lei 等, 2023）。常见的数据驱动模型主要通过分析观测点的单点测量值，捕捉历史变形数据与外部因子（如降雨）之间的时间相关性。相较于滑坡的物理机制，这类模型更注重多变量间复杂相关性的建模（Intrieri 和 Gigli, 2016a；Huang 等, 2017；Guo 等, 2020）。

在这一背景下，人工智能，尤其是机器学习及其分支深度学习，在滑坡预测中展现出巨大潜力。例如，许多机器学习方法在预测具有周期性变形的滑坡中表现出较高精度（Wen 等, 2017；Miao 等, 2018a；Deng 等, 2021；Long 等, 2022；Ma 等, 2022；Wang 等, 2022），如支持向量回归（SVR）和极限学习机（ELM）。SVR通过核函数映射输入数据至高维空间，从而捕捉复杂非线性变形模式。但这类方法为静态方法，将滑坡预测建模为静态回归问题，难以有效刻画滑坡变形的动态特性（Xu 和 Niu, 2018）。

因此，近年来涌现出考虑时间序列特征的动态建模方法。深度学习通过建模复杂的非线性关系和隐藏模式，进一步提升了预测能力（Lusch 等, 2018；Yang 等, 2019；Pei 等, 2021；Mousavi 和 Beroza, 2022）。其中，循环神经网络（RNN），尤其是长短期记忆网络（LSTM），在滑坡变形预测中取得广泛成功。例如，LSTM在预测白家堡滑坡变形方面，优于BP神经网络与SVR（Yang 等, 2019）。

不同深度学习模型在滑坡预测中的适用性存在显著差异。例如，CNN与BP神经网络可通过建模滑坡的内外部关系，在空间分析中展现出较高精度（Azarafza 等, 2021；Nikoobakht 等, 2022）；但在滑坡变形时间预测方面，综合对比研究表明，GRU和LSTM模型由于能捕捉时间序列中的非线性动态特征，预测表现更优，而CNN模型则相对不足（Nava 等, 2023）。表1总结了当前主流AI方法在滑坡变形预测中的优缺点。

表格 1 ：常见基于人工智能的滑坡形变预测方法的优缺点。

方法	优点	缺点
SVR	能够处理短期和样本量有限的数据集（Xiang 等，2024）。	忽略了位移的时间相关性（Miao 等，2018b）。
ELM	以较少的超参数实现良好的泛化能力，适用于实时预测（Cao 等，2015；Huang 等，2017）。	位移预测结果受输入层与隐藏层之间随机连接权重的影响较大（Zhou 等，2018）。
BPNN	能够捕捉多维滑坡数据中的复杂非线性模式（Guo 等，2019）。	缺乏循环连接，限制了对时间依赖性模式的建模能力（Liu 等，2021）。
RNN	可有效建模滑坡形变时间序列数据中的时序动态特征（Chen 等，2013）。	由于梯度消失问题，难以学习位移时间序列中的长期关联（Ma 等，2020）。
LSTM	能够利用时间序列数据中的长期相关性，预测滑坡位移趋势（Xu 和 Niu，2018；Zhang 等，2021a）。	难以融合时间信息以外的多样化因素（Liu 等，2020b）。
GRU	相比 LSTM 参数更少，能够建模时间动态，对短期和中期位移预测结果可靠（Zhang 等，2022a）。	在利用位移趋势中的长期关联方面能力可能受限。
CNN	在从地理空间数据中提取空间特征方面表现出色（Nikoobakht 等，2022）。	难以捕捉滑坡位移的时间变化，时序依赖性建模往往不足（Nava 等，2023）。

尽管AI模型在滑坡预测中表现出巨大潜力，但仍面临四方面关键挑战：

1. 时空相关性缺失：滑坡变形具有系统性和时空相关性，某一观测点的运动与其他区域活动密切相关（空间上）并受历史与未来事件影响（时间上）。多数AI模型以局部观测点为单位，忽略整体滑坡的联系，无法识别潜在的级联破坏风险。

2. 局部异质性未充分建模：不同监测点受材料性质和地质结构等内部因素影响，即使在相似外部条件（如降雨、湿度）下，也表现出不同的变形响应。但当前AI模型对这一局部差异性缺乏建模与解释。

3. 输入特征局限：多数模型侧重于变形参数，忽略了地质、气象、地形等外部因素与内部条件的耦合影响。一些新研究已尝试引入时间变化的外部变量，但对滑坡点本身的内部特征考虑不足。

4. 模型缺乏可解释性：AI模型（尤其是深度学习）常被视为“黑箱”。滑坡预测涉及高风险、高成本决策，需更加谨慎选择算法。因此，研究者呼吁发展可解释的AI方法，提升模型透明度（Sun 等, 2022；Dahal 和 Lombardo, 2023）。

近年来，Transformer 架构与注意力机制的引入，为提升模型可解释性提供了新契机。Transformer模型能识别关键特征与影响因子，挖掘潜在时序模式（Wen 等, 2023），为深入理解滑坡变形提供新的视角。

本研究提出一种融合领域知识、考虑时空相关性、具备可解释性的深度学习框架，用于滑坡变形预测。研究目标在于：

• 揭示滑坡变形中内外因素之间复杂的相互作用，提升预测能力；
• 空间维度：通过融合多个观测点数据，挖掘滑坡整体动态趋势与关键活动区域；
• 时间维度：结合每个观测点的领域知识，动态建模外部触发因素（如降雨）与内部特性（如土壤成分）之间的相互作用，识别局部变形模式；
• 采用 Transformer 模型作为解释性深度学习框架，引入注意力机制，识别并量化关键因素与时序特征，从而挖掘潜在的变形机制。

本文贡献如下：

1. 提出一种融合领域知识、考虑时空相关性的可解释深度学习滑坡变形预测方法，揭示变形模式背后的内外部驱动机制；
2. 从整体与局部两个层面探讨滑坡对不同因素的响应，将滑坡建模为互联子区域网络，并融合观测点内在特性与外部环境信息；
3. 识别并量化影响滑坡变形的关键因素，揭示其时间演化特征；
4. 在三峡库区与青藏高原滑坡案例中验证了方法的适应性与有效性，结果表明该方法能够揭示符合滑坡物理过程的关键时空模式。

2. 背景

2.1 概述

本研究聚焦于中国的两类典型滑坡案例，它们在预测中各具挑战性。
第一类是水库型滑坡，广泛分布于三峡库区，以受水位波动和降雨触发的阶跃式位移为特征。这类滑坡的变形具有强烈的阶段性，极度依赖外部因素（见图1）。因此，准确捕捉水位、降雨与滑坡变形之间的相互作用，并识别潜在诱因与未来事件的预测，对预测方法提出了更高要求（Yang 等, 2023）。

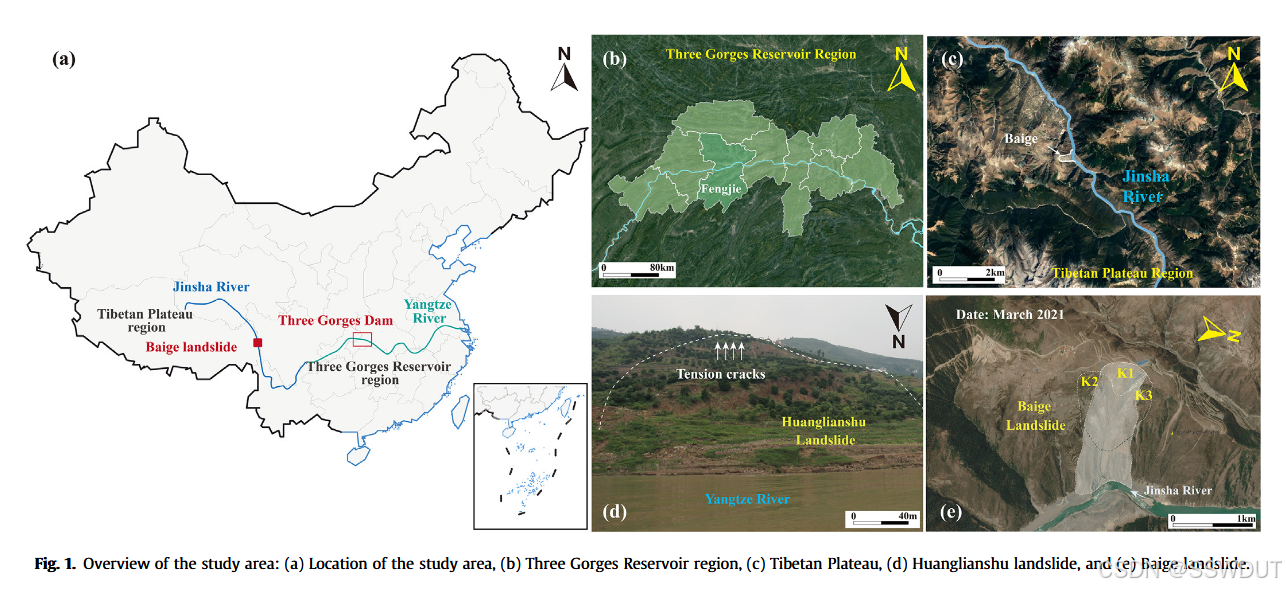
第二类是蠕滑型滑坡，如金沙江下游（东南青藏高原） 的滑坡，表现为缓慢且持续的变形，但也可能在无明显预警的情况下突然转化为灾难性破坏。由于地质结构异质性强和降雨零散不稳定，大多数时间序列外推方法难以预测此类滑坡的变形演化及加速趋势。

当前亟需一种方法，能够对滑坡变形的阶段性过渡进行早期识别与特征刻画，以防止灾难性事件的发生（Murphy 等, 2022；Urgilez Vinueza 等, 2022）。

在这两类滑坡案例中，我们分别构建了包含“知识”和“数据”的输入数据集：

• 知识指通过文献资料获取的信息，例如对岩土工程性质的定性描述。滑坡行为通常受特定地质因素影响，可在某些监测区域识别出。这类分类信息可作为先验知识使用。例如，监测点的标签有助于识别滑坡体内不同部位的差异。

• 数据则包括来自多种来源的时间序列测量数据，如气象数据和滑坡行为观测数据。这种异构数据集合有助于从多角度分析滑坡在不同地质条件和诱因机制下的时空动态特征。

因此，所采用的深度神经网络不仅能考虑各站点独特的地质特性，还能反映每个诱因机制的特殊性。

2.2 黄莲树滑坡的数据与知识获取

第一个案例研究聚焦于三峡库区的水库型滑坡的灾前变形预测。该区域滑坡风险极高，受到恶劣天气、复杂地质条件和人类活动的共同影响。近年来，该区极端气候事件频发，加剧了滑坡风险。

我们的研究对象为位于重庆奉节县、长江右岸的黄莲树滑坡（坐标：北纬31°22′033″，东经109°45′058″）。从空中俯视，该滑坡呈“圆椅状”分布，坡向为350°以上，坡度介于5°至30°之间。滑坡体长约700米，宽约650米，前后缘高差约120米。滑体材料为含碎石的黏土碎块，中部厚、两侧薄。

根据其组成和渗透性差异，滑坡可分为三个区域：

• 上部区域：为渗透性强的碎石土；
• 中部区域：为夹杂碎石土的黏性土；
• 下部区域：为薄层砂土与黏土。

其中，上中部因颗粒粗大、结构松散，降雨时水易渗入；下部因受水库水位变化影响而发生侵蚀与软化，导致裂缝形成。强降雨时，这些裂缝扩大，进一步提高滑体渗透性。相关文献将这些区域归为滑坡危险区。降雨入渗和水库水位下降共同诱发滑坡活动。

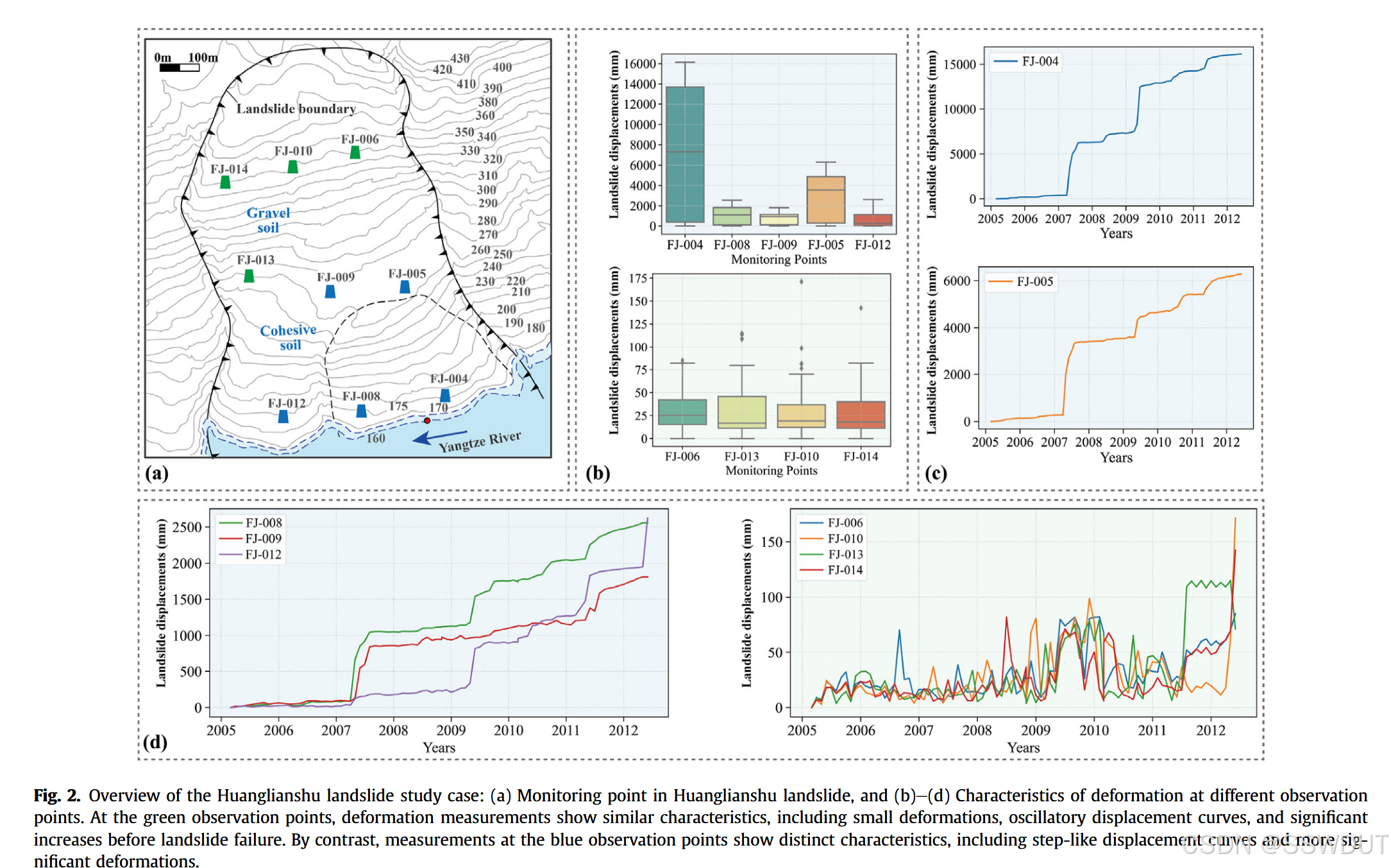
黄莲树滑坡的前缘在 2012年5月31日发生了严重变形。自2003年起，该滑坡通过GPS系统进行了持续监测。我们收集了2005年3月1日至2012年6月1日期间的现场监测数据（累计位移），数据频率为月度采样，共9个监测点，记录内容包括变形数据、降雨量和水库水位。

我们根据滑坡文献中的定性分区，将监测点划分为危险区、非危险区和近危险区，并结合滑坡体内的土壤类型（主要为黏性土和碎石土）。监测点编号为 FJ-004 至 FJ-014，代表不同位置的局部变形行为。

由于原始数据存在大量缺失值，我们剔除了缺失率超过70%的监测点，以减小数据缺失对模型影响。

通过黄莲树滑坡数据，我们观察到滑坡体内变形模式存在明显差异：

• 前缘位移量大，呈现明显的拐点和周期性变化；
• 中部和后缘变形较小，但偶有突变发生。

这种变形差异反映出滑坡各区域对诱发因素的响应存在异质性，主要受水库水位变化和降雨强度差异影响。

结合以往研究与实地调查，已明确指出，降雨与水库水位变化是黄莲树滑坡的主要触发因素。例如，水库水位的周期性波动会引起滑坡体周期性“卸载”，从而导致滑坡变形发生明显的阶跃变化，这一现象可追溯至复杂的热-水-力相互作用机制（Ye 等, 2022）。水位变化会显著影响滑体的渗流场与应力水平。

据分析，黄莲树滑坡的直接诱因是 2012年的强降雨。在 2007年的大降雨后，部分监测点附近已经出现明显变形迹象；2012年5月的大雨则导致：

• 坡体边缘两侧产生剪切张裂缝，
• 中上部出现横向张裂缝，
• 前缘产生隆起型张裂缝，

这些构成了当前滑坡的状态（见图3）。

图4a 展示了黄莲树滑坡的位移时间动态过程，揭示了降雨与水库水位变化之间的相互作用，显示出滑坡位移在水库卸载阶段的明显阶跃变化。图4b 通过皮尔逊相关系数量化了各监测点处水库水位、降雨与滑坡变形之间的关系：

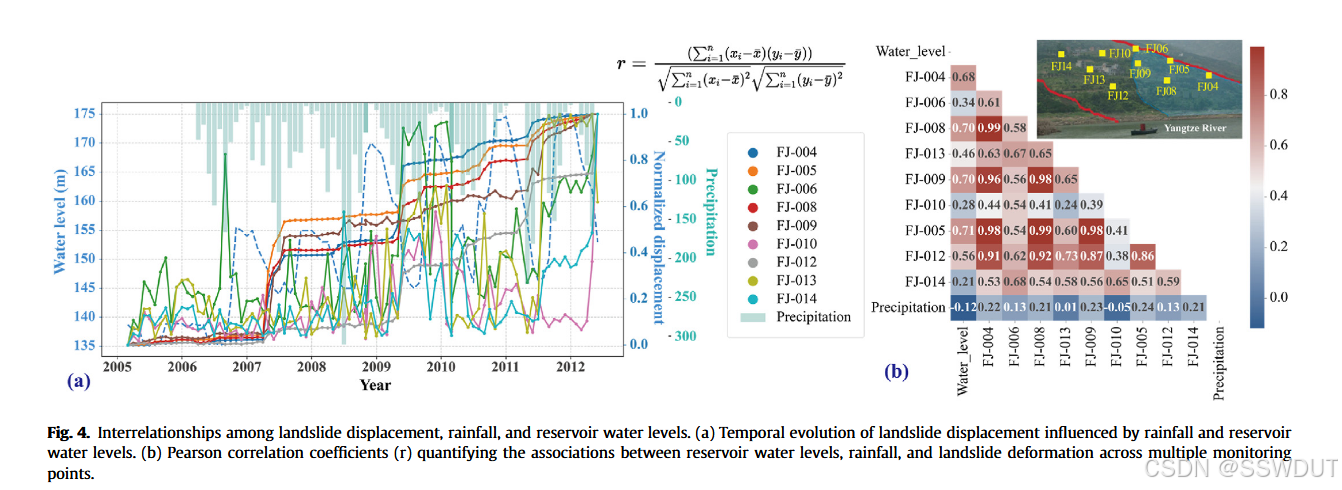
• 水库水位与滑坡位移呈强正相关，
• 降雨与滑坡位移呈中等正相关。

相关性在滑坡体前缘最强，向中部和后缘逐渐减弱。

基于上述分析，我们识别出多个在水库型滑坡预测中具有代表性的重要预测因子：

1. 多个监测点的时间变化位移数据；
2. 地面仪器记录的水位与降雨数据；
3. 包含危险等级、土壤类型与监测点标签等分类信息。

预测目标变量为监测点的位移测量值。值得注意的是，位移时间序列由多个方向的位移分量组成。我们通过计算位移向量的欧几里得范数（即各方向位移分量平方求和后再开方）整合这些分量，从而准确反映滑坡体的整体空间变形状态。

2.3 白格滑坡的数据与知识获取

第二个案例研究位于青藏高原，该区域具有独特的地质与气象条件。多种地质与气候因素（如内部地质构造、深切河谷与降水）共同作用，导致滑坡机制极其复杂（Zhang 等，2021b）。当坡面受到强烈风化，其力学性能与结构完整性会显著下降；在此基础上，若受到地震和降雨等外部驱动因素影响，地质条件将进一步恶化，从而显著增加滑坡风险。

白格滑坡（N31°40′57.87″；E98°42′06.29″）是典型的具有深部重力变形、长期蠕动，最终突发坍塌特征的滑坡案例。该滑坡位于一个高应力缝合带内，长期受到河流侵蚀与风化作用的共同影响（Fan 等，2019b；Liu 等，2020a）（见图 5）。据研究，该滑坡可能起源于20世纪60年代，长期处于缓慢但显著的变形过程（Chen 等，2021）。类似的长期蠕滑型滑坡在发生突变性加速后，可能造成灾难性后果，白格滑坡就曾在突发加速后两次堵塞金沙江。由此可见，了解并预测这类滑坡的演化过程对于减轻人员伤亡和财产损失至关重要。

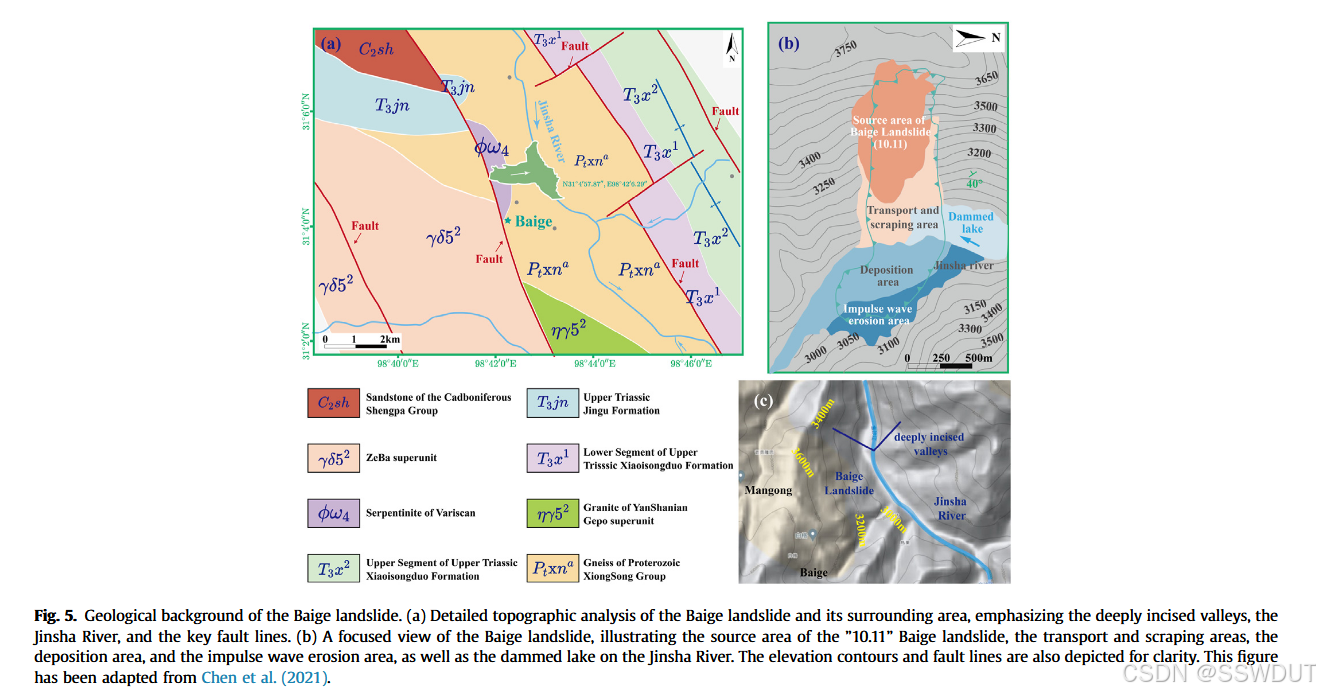
2018年发生两次连续滑坡事件后，在白格滑坡明显的主裂壁后方发现了多个裂缝，表明应力重新分布引发了三个陡峭的自由面。滑坡源区存在多个滑动体。详细调查将滑坡区域划分为三个主要变形区：K1、K2 和 K3，并在这些区域部署了多套全球导航卫星系统（GNSS）设备用于变形监测，同时配置了用于测量环境温湿度的传感器。

除了K1-K3区域外，K2区南坡也被划为K4监测区域。在每个区域内，根据调查结果将监测点设置在裂缝等关键位置，以精准捕捉滑坡关键变形特征。这种针对性的监测布设方式，确保各区域获取最具信息量的数据。

白格滑坡的监测记录在不同时间分辨率下开放获取，如10分钟、3小时和24小时等。这些不同时间分辨率的记录涵盖不同监测点与不同时段，具体细节可见附录信息。本研究使用了3小时与24小时采样频率的数据，删除了缺失值较多的记录，并仅保留时间序列长度与采样频率一致的位移数据。最终构建的白格滑坡数据集详见附录，涵盖了多个监测点的不同时段的累计位移观测数据与实时坐标信息。本次数据采集始于2019年，不仅可用于研究2018年滑坡事件之后的演化过程，也为未来变形模式的预测提供关键因子识别依据。本研究的白格滑坡数据采集截至时间为2022年8月1日。

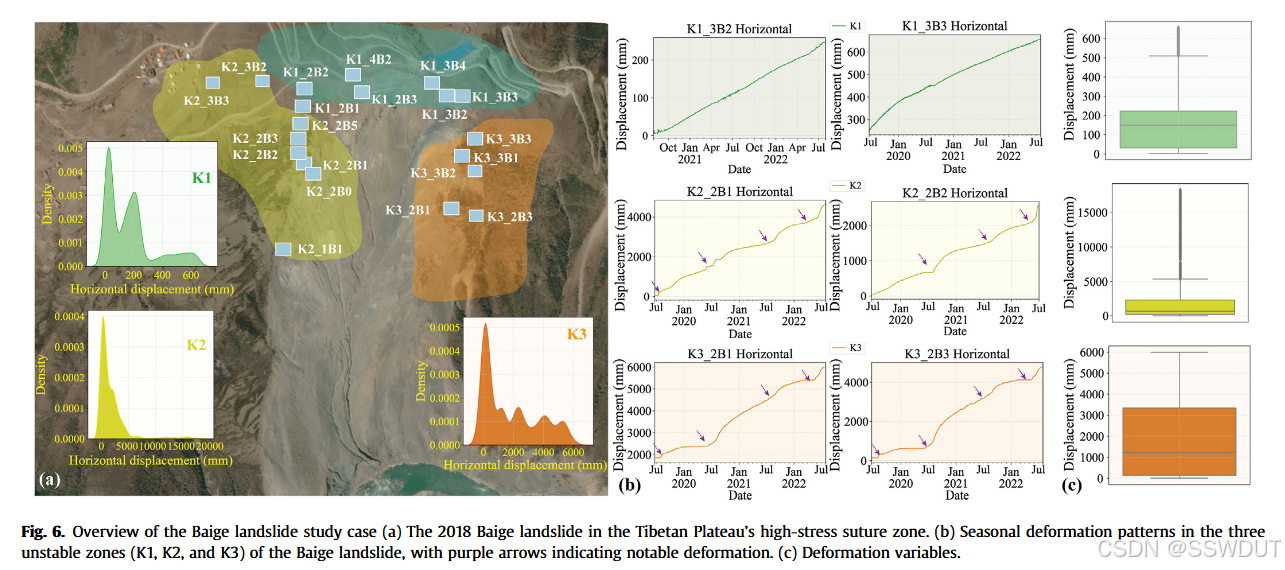
图6展示了白格滑坡在滑坡事件后期的变形记录。自2018年两次大规模滑坡以来，滑坡体持续发生变形，尤其在夏季出现变形加速。图6b 展示了 K1、K2 和 K3 三个不稳定区域内不同的变形模式。其中，K1区域变形较为稳定线性增加，而K2 与 K3 区域在每年六月（雨季来临前）会出现显著突增。滑坡变形具有显著的年度与季节性波动特征（附录图 A6 和 A7）。K1 区呈现近线性增长趋势，而 K2 和 K3 在 10 月至次年 5 月期间基本稳定，但夏季则会快速加速，其中 K3区变形最为剧烈。变形加速的时间点与季风性降雨到来高度一致，表明降水引起的孔隙水压力变化可能是其主要诱因（Handwerger 等，2022）。

根据已有研究，多个关键因素促成了白格滑坡的发生。构造活动与金沙江下切导致该区域地形陡峭、峰谷高差显著，为滑坡提供了不利地质背景。高水位增强了地表径流并加剧了岩体的侵蚀。同时，冰雪快速融化也可能诱发此前稳定的边坡发生滑动。在暴雨等极端条件下，白格滑坡中潜在的不稳定区域更容易失稳。

因此，本研究选择以下变量作为预测模型的输入特征：

1. 来自多个监测点的时间变化位移数据；
2. 地面仪器测得的降水、气温与湿度数据；
3. 不稳定区域及监测点的分类标签信息。

温度和湿度数据是关键的外部环境指标——快速的冰雪融化可能引发原本稳定边坡的失稳。此外，我们使用“K1、K2、K3”区域分类作为标签标识，用于代表滑坡体的不同子区域，这些分类反映了区域周边地质环境的特征，也承载了领域先验知识。例如：

• K1 区：由片麻岩/片岩构成，具有多尺度弧形裂缝；
• K2 区：由强风化含碳页岩构成，也有多尺度裂缝；
• K3 区：由千枚岩构成，未见蛇纹岩，下伏片麻岩，裂缝较多（Fan 等，2019b）。

这些地质分类具有实际意义，能反映每一区域的局部地质结构差异。

3. 方法论

3.1 总览

我们提出了一种滑坡变形预测方法，将领域知识融合进可解释的深度学习框架中，并考虑了时空相关性（见图 7）。该方法首先通过对观测数据（如降水、水位波动等外部环境影响的时间序列）与领域知识（如岩性等内部条件的实地调查报告）进行表征，从而增强了模型对时空特征的可预测性。

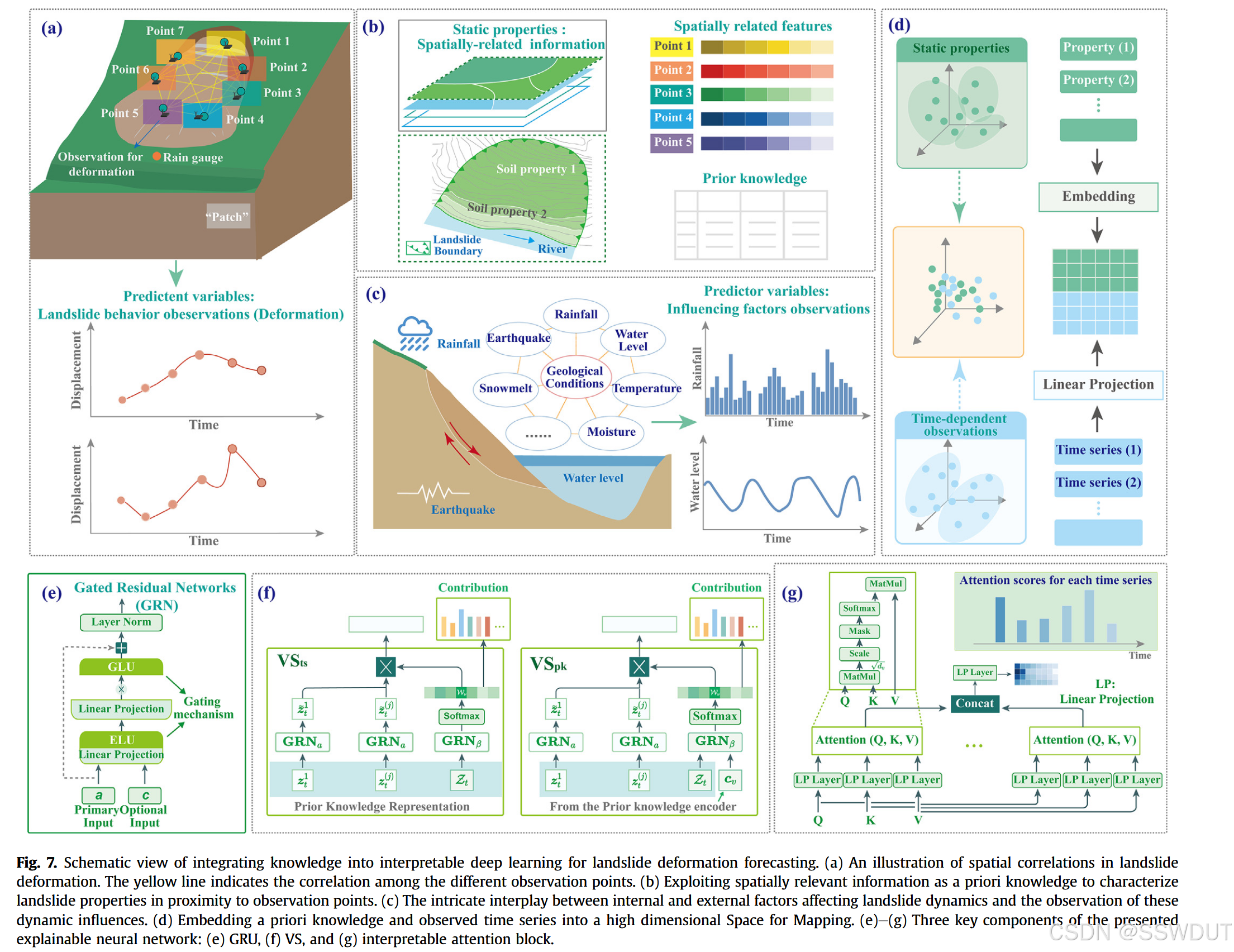
其次，我们基于 Transformer 架构构建了一种自解释神经网络模型，用于融合知识与数据。该模型不仅提升了预测能力，还揭示了关键影响因子及其对应的时空特征，从而增强了人们对深度学习预测滑坡变形机制的理解。

我们所提出的预测框架核心依赖于 Temporal Fusion Transformer (TFT) 模型，这是一种已被验证具有良好预测能力的深度学习架构，用于剖析滑坡预测能力的来源。该框架的整体结构如图8所示，其中关键模块围绕滑坡变形预测中的主要挑战设计并组织：

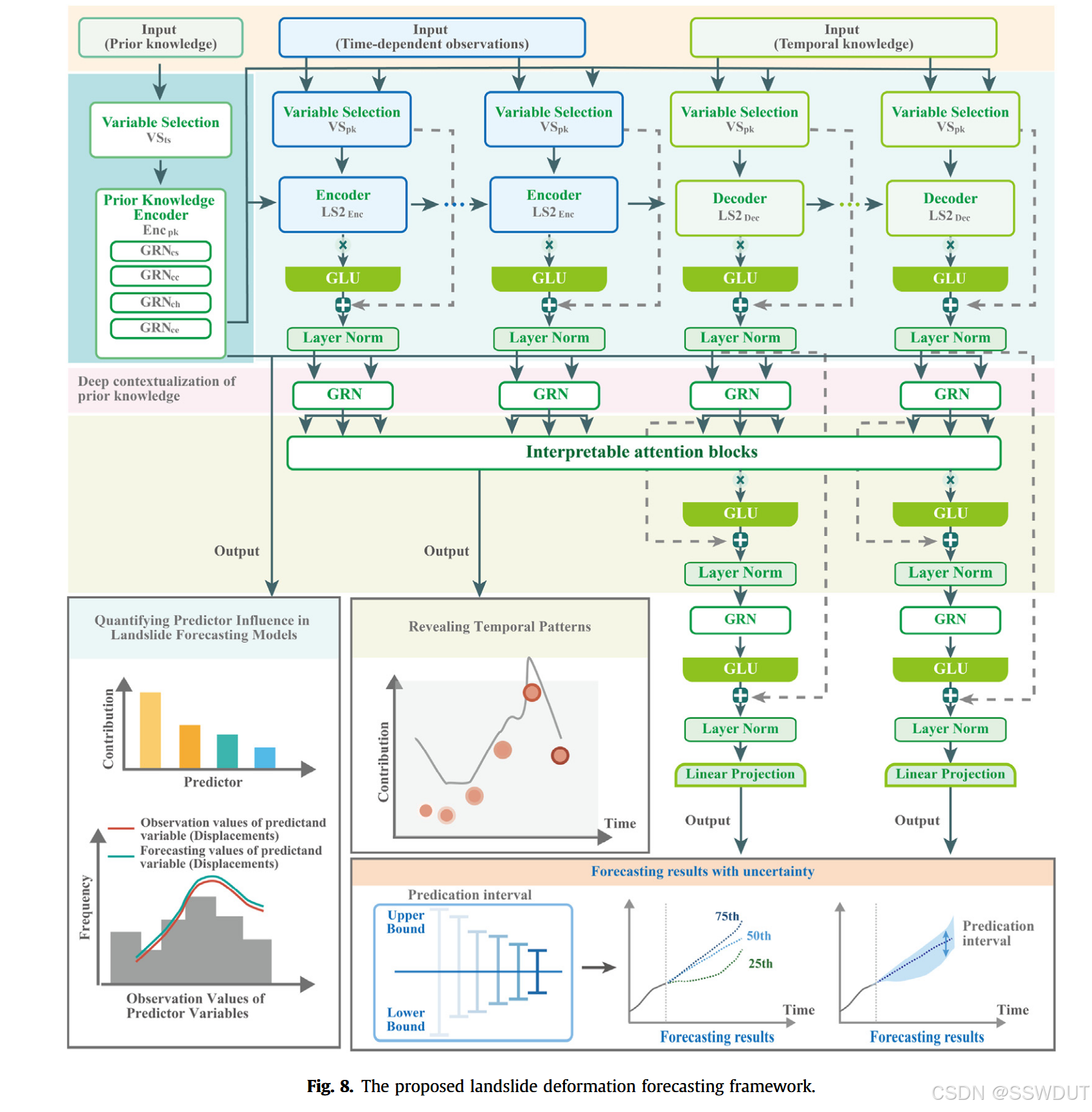
• 门控机制（Gating Mechanisms）：作为基础模块，将观测数据与领域知识融合，从而增强神经网络对空间的感知能力；
• 动态特征选择模块（Dynamic Feature Selection Blocks）：在多个时空尺度上对融合后的信息进行筛选和解释，识别滑坡行为的关键驱动因素；
• 基于 LSTM 的编码器-解码器结构：进一步维持并增强已选特征的时间动态特性；
• 可解释注意力机制（Interpretable Attention Mechanism）：整合编码器与解码器输出，深入洞察时序模式与多因子对不同空间区域滑坡行为的影响。

3.2 融合数据与知识的门控机制

为了提高模型的预测能力，我们增强了神经网络对滑坡响应（包括内外因子）在整体与局部空间层面的感知能力。首先，我们将多个观测点的时间序列数据（包括滑坡变形、外部影响、内部属性）统一嵌入到共享的高维空间中。然后，借助门控机制对与滑坡行为密切相关的信息进行选择性整合。

数据和先验知识会被转换成维度为 $d\_m$ 的向量，其中 $d\_m$ 是超参数。具体过程如下：

• 时间相关的滑坡变形量或驱动变量通过线性投影进行转换；
• 领域知识则使用词向量（word embeddings）表示；
• 每个第 $j$ 个输入变量最终映射为一个向量：$z\_t^{(j)}\in {\mathbb{R}}^{d\_m}$；

接下来使用 门控残差网络（GRN, Gated Residual Network） 块，识别和利用多模态输入中最相关的特征与关系，从而捕捉滑坡行为的驱动因素及其空间影响。

GRN 包括两种门控机制：

(1) 指数线性单元（ELU）：

$$\text{ELU}(x)=\{\begin{array}{ll}x,& x>0\\ \alpha (\exp (x)-1),& x\le 0\end{array}$$

其中，参数 $\alpha$ 控制负半部分的饱和值。

(2) 门控线性单元（GLU）：

$$\text{GLU}(x)=(x\ast Q_1+b_1)\odot \sigma (x\ast Q_2+b_2)$$

• $Q\_1$, $Q\_2$：线性变换的权重矩阵
• $b\_1$, $b\_2$：偏置项
• $\sigma (\cdot )$：sigmoid 函数
• $\ast$：矩阵乘法
• $\odot$：逐元素乘积

(3) GRN 的基本操作如下：

GRN 接受主输入 $a$ 和可选的上下文输入 $c$，逐层提取更具信息量的表示 $g\_1$：

$$\text{GRN}(a,c)=\text{LayerNorm}(a+{\text{GLU}}_u(g_1))$$

$$g_1=W_{1,u}{g}_2+b_{1,u}$$

$$g_2=\text{ELU}(W_{2,u}a+W_{3,u}c+b_{2,u})$$

• $\text{LayerNorm}(\cdot )$：层归一化函数，对输入的特征维度进行归一化处理；
• $W\_1,u,W\_2,u,W\_3,u$：权重矩阵；
• $b\_1,u,b\_2,u$：偏置项；
• $\text{ELU}(\cdot )$：指数线性单元函数，如前述；

GRN 结构实现了信息压缩与增强，通过门控机制筛除冗余或无关的信息，为模型提取更有效的特征。

3.3 用于揭示滑坡行为驱动因素的特征选择模块

为了提升模型的可解释性，我们采用架构中的 变量选择（Variable Selection, VS）模块，识别在不同尺度和时间段内影响滑坡行为的关键因子。

首先，GRN_a 会独立地过滤每个输入向量，区分有用特征和噪声信息。过滤后的向量表示为：

$${\tilde{z}}_t^{(j)}={\text{GRN}}_a(z_t^{(j)})$$

第二部分使用类注意力机制操作。在此，GRN_b 接收扁平化后的输入：

$$Z_t=[z_t^{(1)},z_t^{(2)},...,z_t^{(n_X)}{]}^T$$

同时还接收代表先验知识的附加输入变量 $c\_v$。通过 Softmax 激活函数对 GRN_b 输出进行归一化赋权，权重向量表示为：

$$W_v=\text{Softmax}({\text{GRN}}_b(Z_t,c_v))$$

该权重矩阵 $W\_v$ 表征了每个输入变量对滑坡变形预测的贡献，具有良好的可解释性。最终输出为自动筛选出的滑坡预测所需的有效信息：

$${\tilde{z}}_t=\sum _{j=1}^{n_X}{W}_v^{(j)}\cdot {\tilde{z}}_t^{(j)}$$

如图2所示，用于时间相关特征的 VS 模块（记为 $VS\_ts$）与用于先验知识的 VS 模块（记为 $VS\_pk$）存在差异，主要在于 $VS\_pk$ 包含了来自先验知识编码器（Encpk） 的上下文输入 $c\_v$。

Encpk 负责将滑坡的局部属性、时间变形行为与外部变化关联起来。四个 GRN 模块从中提取有意义的先验知识表示，协助模型学习：

• GRN_cs：帮助 $VS\_ts$ 选择时间相关与静态特征；
• GRN_cc, GRN_ch：分别初始化 LSTM 的 cell 状态与 hidden 状态，用于发现局部时间模式；
• GRN_ce：在预测变形前进一步整合先验知识。

3.4 用于保持变形动态的基于 LSTM 的编码器-解码器

在 基于 LSTM 的编码器-解码器（LS2） 中，LSTM 充当位置编码器的角色，使模型每一层的高阶表示对应于特定时间点，从而保持时间序列的顺序完整性，并捕捉时间依赖关系。

LSTM 的状态初始化时使用来自先验知识的嵌入向量 $c\_h$ 与 $c\_c$，使得上下文依赖于先验知识，同时保留变形的时间动态性。其状态转移过程可表示为：

$$h_t=F(x_t,h_{t-1},c_h)\text{\hspace{1em}(4a)}$$

$$c_t=G(x_t,c_{t-1},c_c)\text{\hspace{1em}(5a)}$$

其中 $x\_t$ 为时间 $t$ 的输入，$F(\cdot )$ 与 $G(\cdot )$ 分别是隐藏状态与单元状态的 LSTM 转换函数。

• 编码器处理静态与未来已知的输入；
• 解码器生成最终的特征提取结果，记作 $\tilde{\iota }(t,n)$；

其中：

• GRN_ch：辅助完成非线性变换；
• GRN_eh：处理由 LS2 得到的时间特征 $\tilde{\iota }(t,n)$ 与来自 GRN_ce 的 $c\_e$，输出最终特征：

$$z(t,n)={\text{GRN}}_{eh}(\tilde{\iota }(t,n),c_e)$$

每个状态都表达了多因素在时间维度上交互作用所引起的动态演变过程。

3.5 用于揭示滑坡区域时间模式的可解释注意力模块

我们采用自注意力机制（self-attention） 来提升滑坡变形预测的可解释性。这种神经网络方法为每个时间点分配注意力权重，从而在预测局部滑坡动态时能有选择地关注相关历史输入。

此外，注意力权重还能量化模型对于特定空间区域中滑坡诱发因素的敏感度。可视化注意力权重，有助于揭示隐藏的时间模式，从而提高预测精度。

设有时间序列 $x\in {\mathbb{R}}^T$，则其对应的查询（Query）、键（Key） 和 值（Value） 矩阵分别为：

$$Q=x{W}^Q,K=x{W}^K,V=x{W}^V,W^Q,W^K,W^V\in {\mathbb{R}}^{d\times d}$$

自注意力得分的计算如下：

$$F_{ta}=A(Q,K)V{W}^V$$

采用多头注意力表示：

$$F_{ta}=\frac{1}{H}\sum _{h=1}^H{A}_{tt}(Q{W}_Q^{(h)},K{W}_K^{(h)},V{W}_V^{(h)})$$

其中，完整注意力函数 $A\_tt$ 为：

$$A_{tt}(Q,K,V)=\text{softmax}\left(\frac{Q{K}^T}{\sqrt{d_k}}\right)V$$

• $A(Q,K)$：衡量历史状态对未来预测的影响；
• $\sqrt{d\_k}$：对维度进行缩放以稳定梯度；
• $\text{softmax}$：用于获得注意力分布；
• $H$：注意力头数量。

最终，通过这种注意力机制，模型不仅提升了预测性能，也提供了对不同时间和空间区域中滑坡变形机制的可解释视角。

4. 结果

我们首先将所提出方法与当前在滑坡预测中占主导地位的深度学习方法——LSTM和GRU——进行了比较，以验证其有效性。该比较突显了本方法在性能和能力上的独特优势。初步评估仅限于单点位形变观测数据，因为这种数据是滑坡监测中的常见实践，从而为与现有基于深度学习的滑坡形变预测方法提供了公平对比。

随后，我们通过深入分析黄连树滑坡和白格滑坡两个案例，评估了本方法在实际应用中的可行性和适应性，重点展示其在识别影响因素和时空模式方面提升预测能力的能力。在这两个案例研究中，我们设计了四种实验场景，以演示将领域知识融合到考虑时空相关性的可解释深度学习框架中，如何显著提升滑坡预测准确性（详见附录图A1）：

• 场景1（ST-NSP）：单目标预测，考虑来自周围监测点的邻近空间测量。该场景不整合先验知识或环境因素。
• 场景2（MT-MPC）：多目标预测，使用监测点分类信息。该场景预测多个滑坡监测点的形变时间序列，不考虑环境因素。
• 场景3（ST-NSP-EV）：单目标预测，考虑环境变量。该场景在场景1的基础上加入了环境因素。
• 场景4（MT-MPC-PK-EV）：多目标预测，融合先验知识和环境变量。该场景在场景2基础上进一步整合了关于地质与岩土属性的先验知识以及环境变量。地质属性与风险等级等定性描述与监测点标签一起被编码为类别变量输入模型。

有关模型配置、优化及评估方法的更多细节，请参阅补充材料。超参数选择基于已有研究中的推荐标准，以避免过拟合，无需额外微调。

为评估所提出滑坡形变预测方法的准确性与可靠性，我们采用了两个时间序列预测常用指标：均方根误差（RMSE） 和平均绝对误差（MAE）。

4.1. 所提出可解释深度学习滑坡形变预测方法的有效性

首先，基于黄连树滑坡数据，我们比较了LSTM、GRU与所提出方法在不同预测步长下对未来趋势的外推能力（见图9）。三种方法在单步预测下均表现良好，但LSTM与GRU在预测步数增加时准确率显著下降。相比之下，所提出方法在长期预测中依然保持稳定的准确率与误差表现，这可能得益于其时间序列注意力模块能有效聚焦于历史位移状态，并调整注意力权重，从而增强了长期预测的稳定性与准确性。

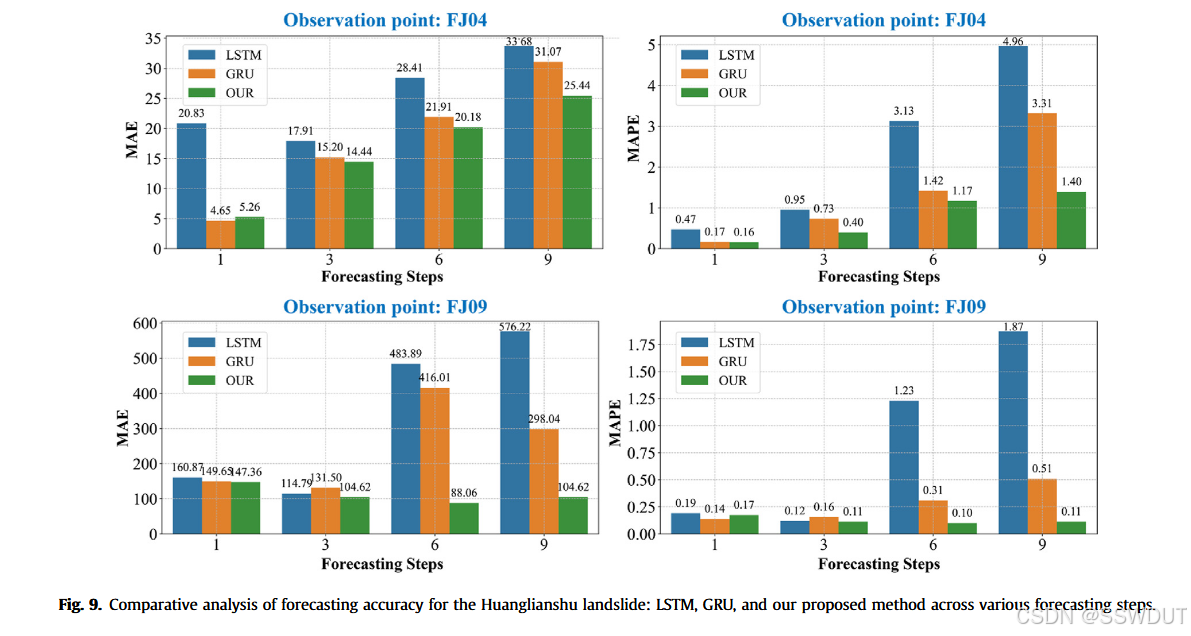
此外，我们使用白格滑坡的高分辨率数据（3小时采样间隔）进行了对比分析（图10）。预测结果中，橙色曲线代表本方法的预测，与蓝色的实际观测数据高度一致。橙色阴影部分表示基于分位数回归生成的预测区间，反映模型预测的不确定性。阴影越宽，表示该时间点预测的不确定性越高。

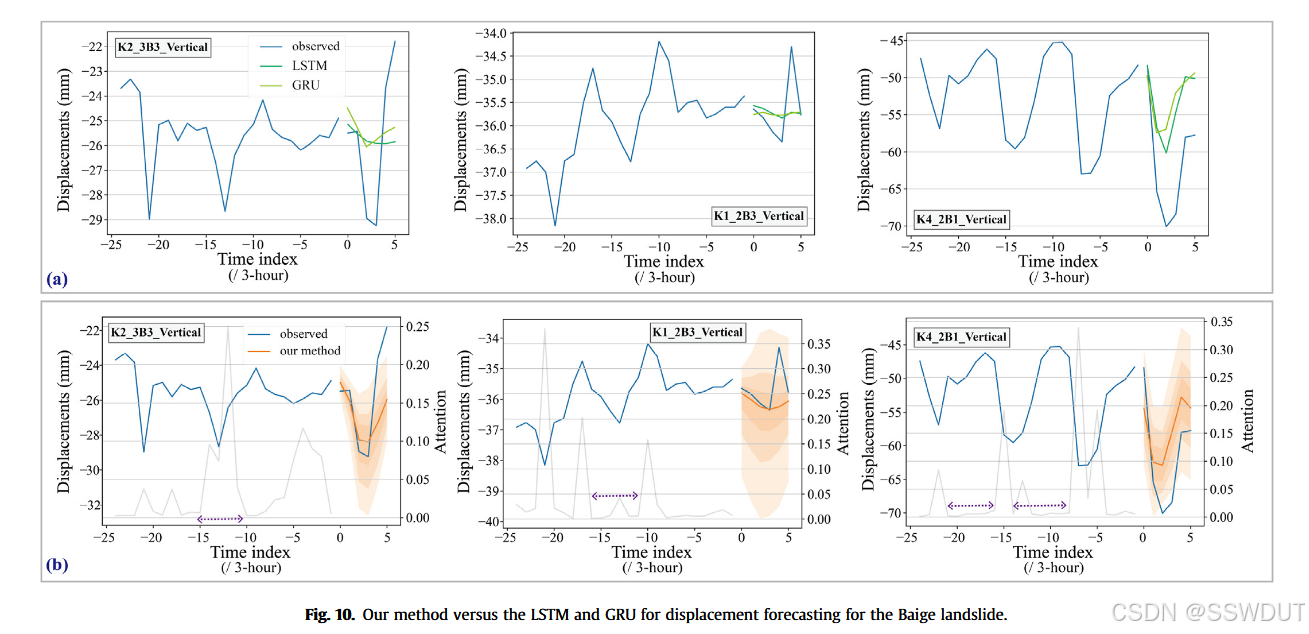
模型的可解释性通过灰色曲线（注意力输出）体现，该曲线表明模型在预测时更重视哪些历史形变状态，揭示了预测过程中的决策依据。灰色曲线中的峰值代表了模型认为关键的时间点，这些峰值通常对应于滑坡演化中的重要变化。通过聚焦于这些关键状态，模型能更准确地外推未来形变轨迹。

值得注意的是，灰色曲线的峰值间隔与形变时间序列中存在的五步振荡周期高度一致，说明模型能够捕捉到滑坡行为中的周期性特征。

4.2. 黄连树滑坡的预测与影响因素解析

通过黄连树滑坡案例，我们从以下三个关键维度验证了本方法在水库型滑坡预测中的实用性与可解释性：

(1) 空间相关性：

我们分析了在不同实验场景下预测性能随监测点空间位置的变化情况，并评估模型如何利用地质背景信息学习滑坡不同区域的差异性形变模式。

(2) 时间相关性：

我们探讨了滑坡形变在各监测点的时间相关性对预测性能的影响；分析历史时间序列长度对预测准确性的影响；并依据模型学习到的时间模式理解滑坡的触发机制。

(3) 影响因素分析：

我们深入分析了提升预测能力的关键因素，明确了哪些因素最有助于预测滑坡形变，并研究其对时空特征建模与预测准确率的影响。

整体而言，所提出的可解释深度学习方法融合领域知识，在预测精度和对滑坡动力机制的理解方面取得了双重突破。这一框架不仅在长期预测任务中展现出优越性能，还能识别影响滑坡形变的关键驱动因素及其时空作用模式，为水库型滑坡的监测与早期预警提供了更具物理意义的决策支持。

4.2.1. 滑坡变形预测中对空间相关性的考虑

我们首先在滑坡体的不同部位和四种实验场景下，使用RMSE评估预测性能的差异。我们分析了位于滑坡前缘的5个监测点以及中部和后缘各4个监测点的表现。结果表明，尽管前缘的变形幅度最大，但预测精度却最高（见图11）。在该区域中，将监测点名称作为先验类别信息，并对多个监测点同时进行预测（MPC场景）可获得最低的RMSE。

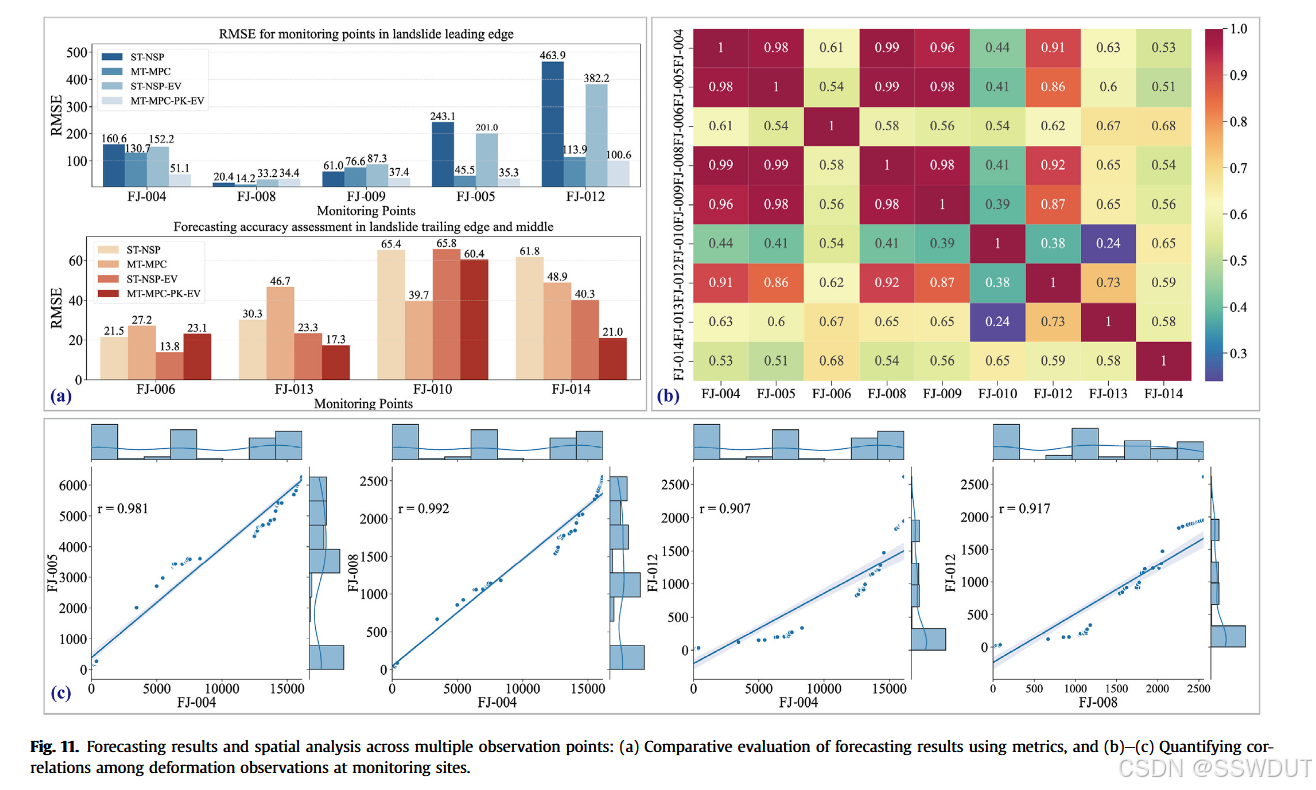
需要注意的是，这一规律并不适用于中部和后缘区域，FJ-006和FJ-013点即为典型例子。在这些区域中，若加入额外的驱动因素信息（EV场景）和岩土性质等地质先验知识（PK-EV场景），预测性能进一步提升。特别是在集成了多源数据和先验知识的最全面场景（MT-MPC-PK-EV）中，预测精度达到最高。

图11b展示了多个监测点之间的皮尔逊相关系数，揭示了滑坡部分区域对外部因素具有同步响应的特征。这种在滑坡前缘监测点之间观察到的强相关性突出了滑坡动力学的互联特性，增强了整体预测的准确性（即对多个监测点的同时预测）。这进一步说明，集成多样的数据源并利用先验知识能够为深度神经网络提供空间感知能力，从而在空间相关性强的区域提高预测性能。

本文提出的可解释深度学习滑坡变形预测方法，通过四种实验场景下多种领域知识集成策略，加强了对空间相关性的理解。在单点预测（ST）场景中，来自其他监测点的变形数据被视为协变量。每个输入变量都可以被量化评估，有助于分析邻近监测点对目标点预测的贡献。

图12a展示了ST-NSP场景中FJ005的预测结果，图12b则分析了不同监测点的变形对该目标点预测的影响。这对于理解在不同变形区间下，各监测点的变形对目标点预测的贡献至关重要。我们选取对预测影响最大的监测点，绘制其预测结果的变化曲线。图中的灰色柱状表示每个变量的分布频率，蓝色和橙色曲线在低频处的一致性反映了模型捕捉罕见事件（如滑坡损伤期间的突然变形变化）的能力。

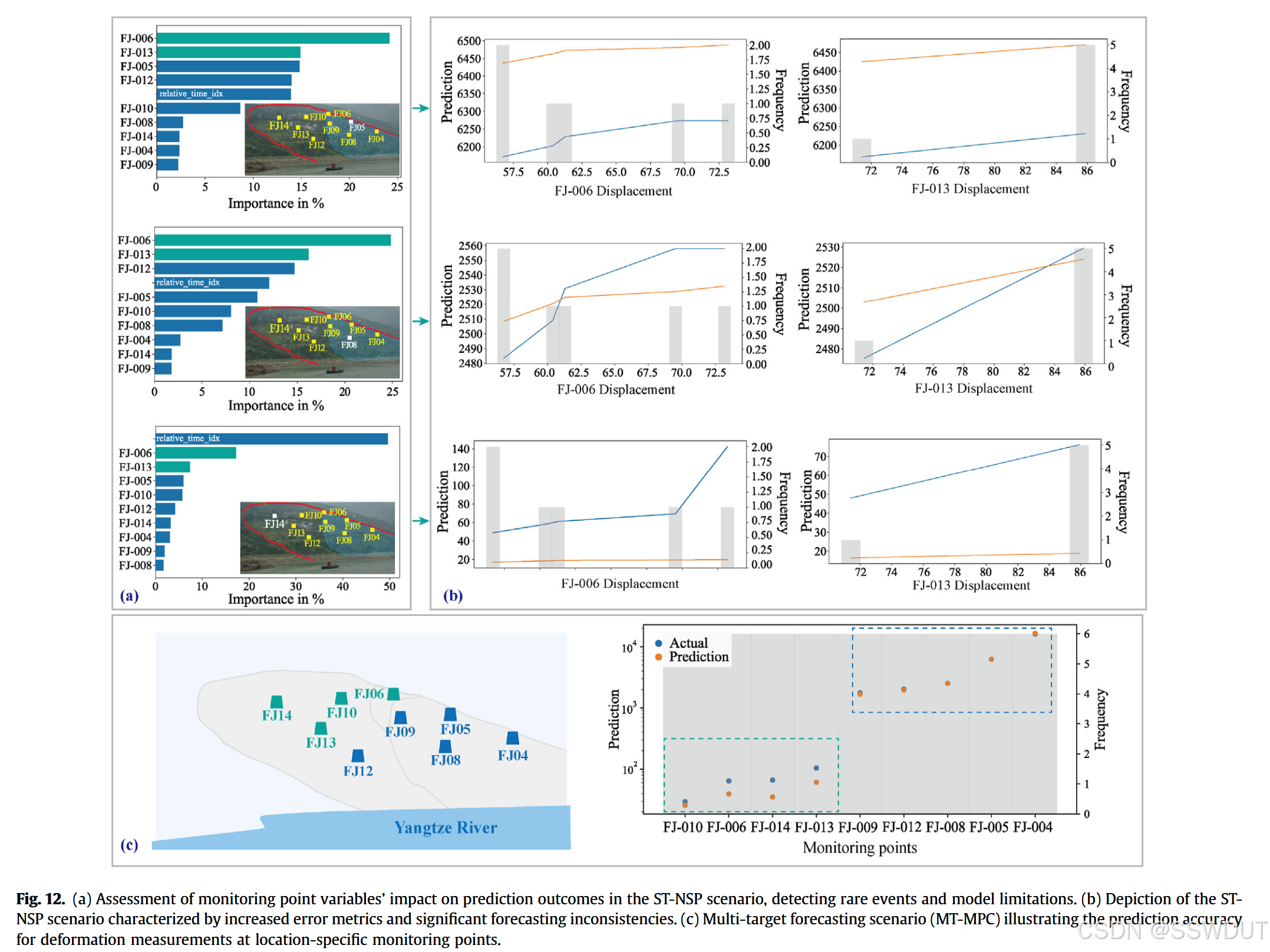
图12c展示了多点预测（MT）场景中多个目标点的预测精度差异。在该场景中，每个监测点被当作一个独立的识别对象，允许同时预测多个点的变形。结果显示，对于具有波动性和突变性的变形数据，神经网络的预测性能较差；相反，当监测点的数据呈现阶梯状变化时，预测效果最佳。这一发现与以往研究一致，强调了在无明显模式情况下预测突发变形的困难。

通过研究滑坡不同观测点之间变形的空间关系，可以洞察滑坡发展和传播的潜力。已有研究指出，空间位移相关性是影响局部滑坡破坏发生的关键因素。例如，若两个点之间的位移相关性较高，则说明它们可能朝同一方向、以相似速率移动，表明滑坡可能在这两个点之间发展出剪切面（Desai 等, 2023）。

4.2.2. 滑坡变形预测中对时间相关性的考虑

图13展示了在不同监测点上，四种实验场景下的滑坡变形预测结果。即使在变形模式大幅波动的情况下，本研究提出的融合领域知识的可解释深度学习预测方法也能实现较高精度（见图13e–h和m–p）。随着更多空间相关先验知识和环境因素的引入，具有相似时间模式的不同监测点数据可以被模型学习，从而实现趋势的高一致性外推（由橙色线表示）。这表明，丰富的上下文提供了一个全局一致且物理合理的滑坡行为视角。

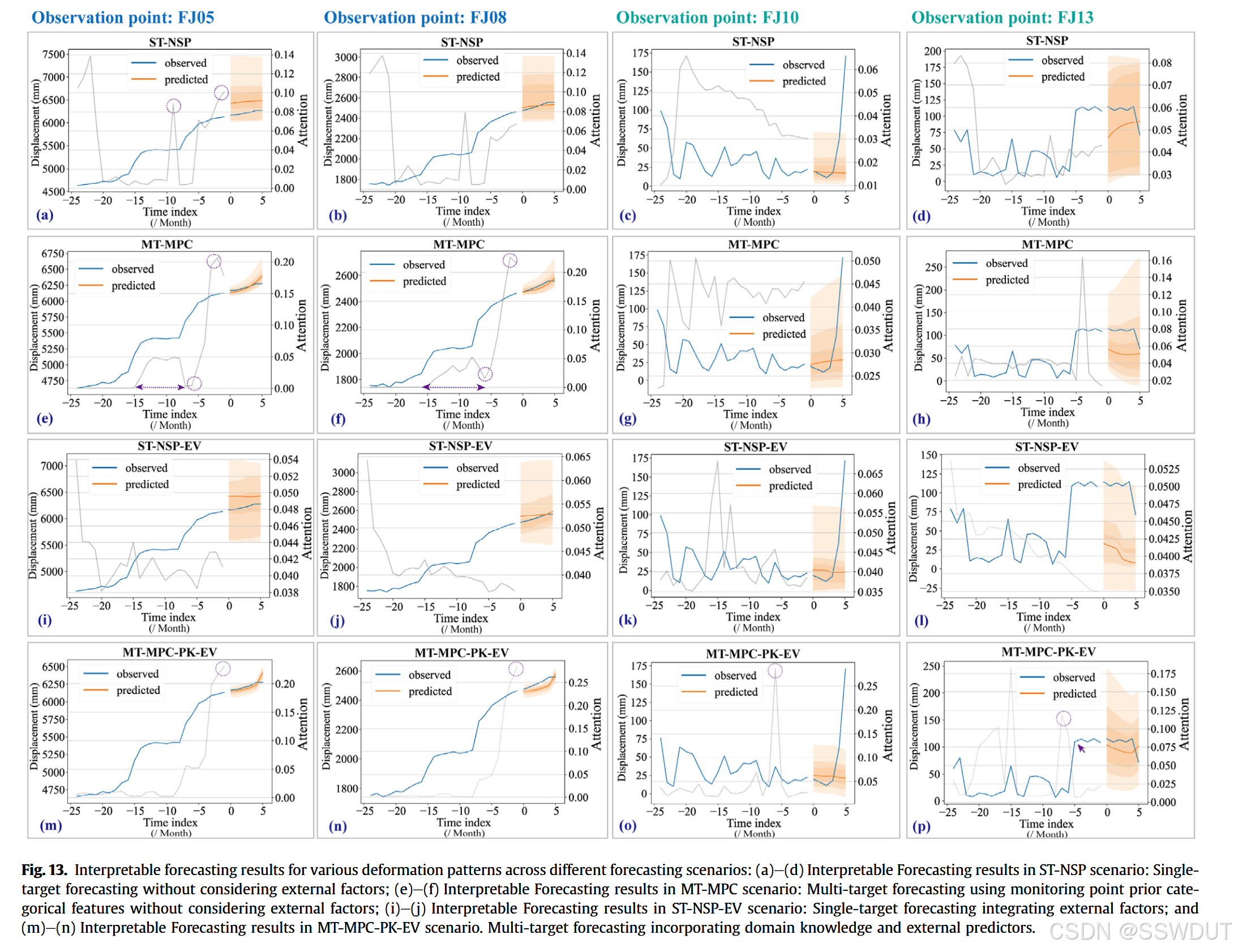
因此，滑坡体不同部位的测量数据（其可能具有相似的驱动机制）可显著影响单个监测点的预测结果。将先验知识与其他预测因子融合，即使在缺乏规律性变化（如阶梯状变形）的情况下，也能实现高精度预测（图13c和d）。

预测不确定性可以作为可靠性评估的指标。例如，在某个监测点出现滑坡速率突然加快的情况下（图13d），虽然模型能准确预测增长趋势，但变形值的快速变化也伴随着更大的预测区间，反映了对该预测结果的低置信水平。

图中灰色曲线代表每个历史输入对当前预测的重要性，展示了模型在面对不同因素时如何优先考虑历史数据的不同时间段。在MT-MPC-PK-EV场景中，当滑坡变形加速时，模型主要依赖于过去3–5天的测量数据（即注意力权重高）；而在变形波动较小的情形下，模型则更重视过去5–10天的数据，利用更长的历史上下文进行外推。这说明将空间特异性知识注入到可解释深度神经网络中，有助于理解每个监测点的历史行为如何在考虑多种内部和外部因素的基础上用于未来预测。

接着，我们评估了所提方法在长时间尺度下的外推能力。通过增加输入序列长度和预测时间跨度，进一步探讨其长期预测能力，特别是在集成先验知识和驱动因素的MT-MPC-PK-EV场景中。我们将预测范围逐步延长至12个月，同时延伸历史变形数据长度至48个月，以确定实现高精度预测所需的时间信息量。

实验设置为：输入序列长度为24和48个月，预测范围为8和12个月，并引入先验的时间变化信息（如年份、月份、季节）以增强模型对时间动态的理解，从而捕捉黄莲树滑坡位移序列中的周期性变化。

结果显示，预测精度普遍随预测时间范围的增加而下降。当使用48个月的历史数据并设定12个月的预测期时，大多数监测点的误差指标显著改善（详见附录图A3）。不过，这种延长历史数据对不同区域影响存在差异。例如，在滑坡前缘区域，预测精度反而下降，可能是由于该区域位移主要受水库水位波动影响，对长期趋势不敏感；而在滑坡体其他部位（如FJ-010和FJ-013点），延长输入长度则提升了预测效果，可能由于更好地捕捉了降雨、季节变化与位移之间的复杂关系。

然后我们可视化并比较不同输入长度下模型从滑坡变形序列中学习到的时间模式，重点关注MT-MPC-PK-EV场景。研究目标是：(1) 理解模型学习了哪些时间模式；(2) 判断这些模式是否具有物理合理性。

图14显示，模型成功捕捉到了水库水位变化与滑坡变形之间的周期关系，包括变形增大前灰色曲线的上升趋势和隐含的周期性模式。当输入长度为48个月时，这些周期性更为明显。尤其在滑坡前缘点（如FJ-012），所学习的周期变化与实际水位变化高度一致。周期波动的幅度随着离前缘距离的增加而减小，反映了滑坡响应的空间异质性。这暗示了水位变化与滑坡活动之间的潜在联系，可能几乎没有滞后时间。

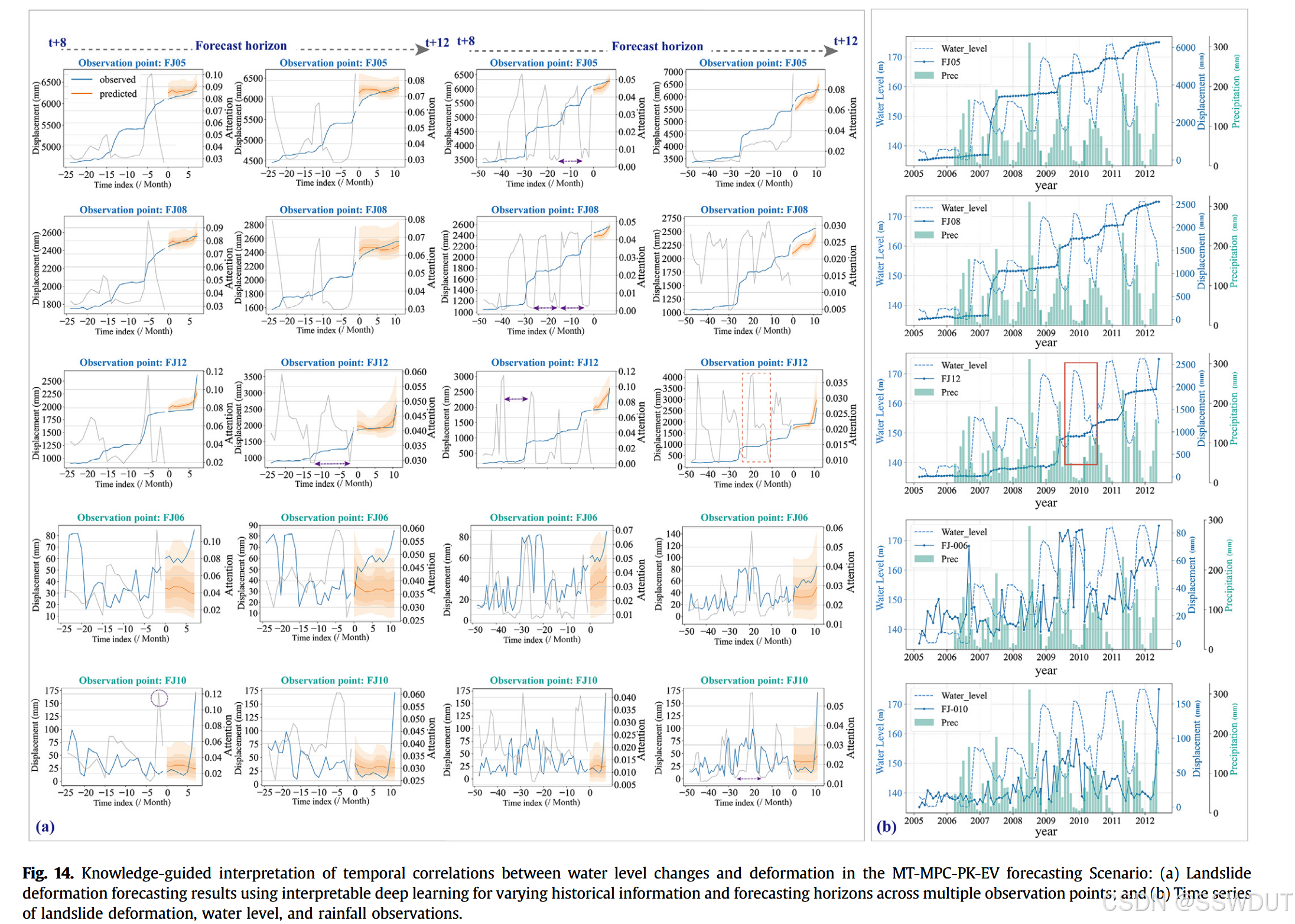
不过，该关系的精确机制仍需深入研究。已有文献指出，水位周期性涨落会通过渗流通道侵蚀、次生孔隙形成及岩体裂隙相互作用等机制影响边坡稳定性（Tang等, 2019a）。此外，图中加速变形期间的阶梯状位移也被模型捕捉到，这通常与水位下降期相对应。已有研究表明，水库水位下降可能诱发内部水流外移，产生不利的渗流压力，从而削弱边坡稳定性并加剧滑坡变形（Song等, 2018；Tang等, 2019b）。

4.2.3. 滑坡形变预测中关键影响因素的识别

在黄连树滑坡案例中，我们基于可解释深度学习的滑坡形变预测方法，定量评估了多种预测因子对预测准确性的贡献。所得的因素排序与专家的认识及滑坡动力学的物理知识（Sun et al., 2016；Zhou et al., 2016a,b）相符。图15a展示了ST-NSP-EV场景下滑坡体内影响因子的显著空间异质性。这种差异可能源于不同区域的敏感性差异，不同区域基于其地理和水文特征对驱动因子有不同响应（Huang et al., 2018）。滑坡前缘邻近长江水体，该区域对水位波动高度敏感。水位上升会导致土壤饱和和软化，削弱岩土体的稳定性，增加失稳风险。此外，水渗透增加滑坡体质量，进一步影响其稳定性（Yang et al., 2023）。相比之下，中心区和后缘受河流水体影响较小，对水位变化响应较慢；后缘区更易受降雨影响，因降雨主导该区土壤含水量及稳定性（见图15b）。

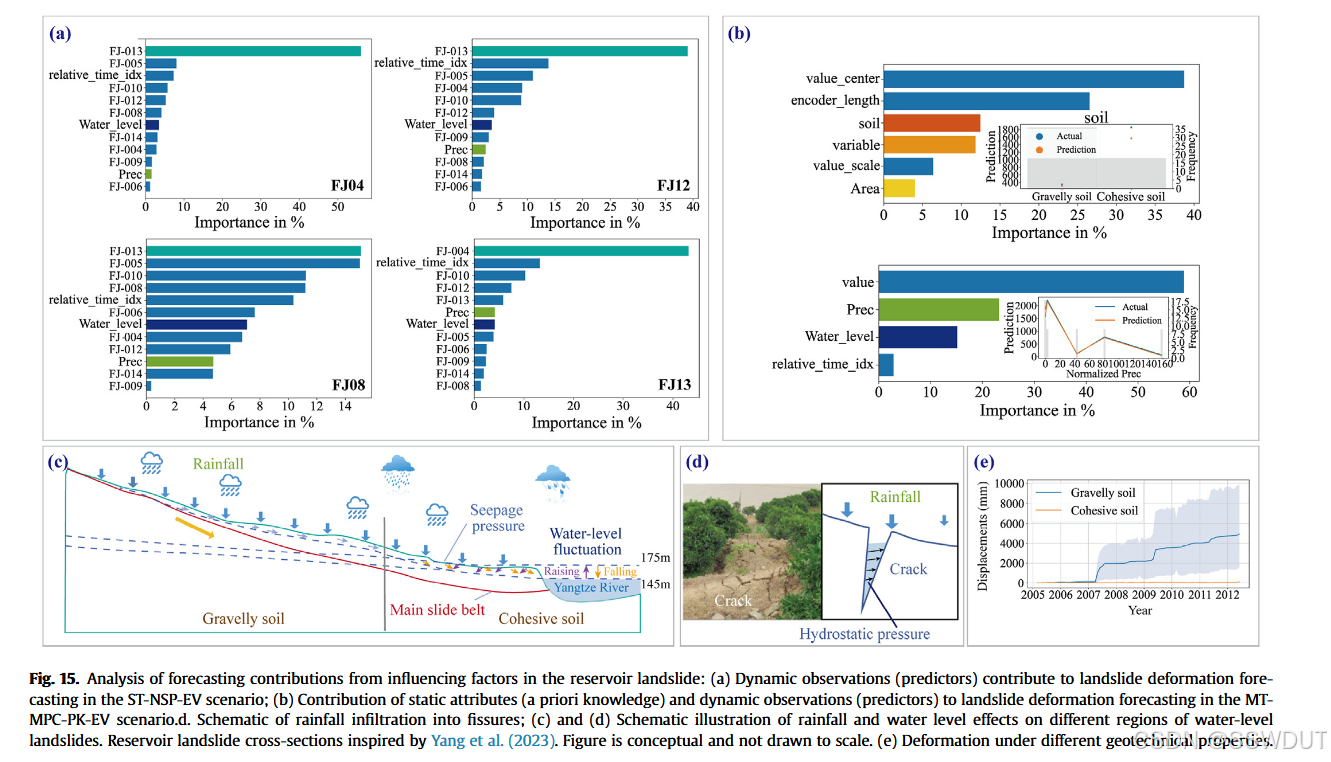
在MT-MPC-PK-EV场景中，图15c定量评估了区域特定的先验知识贡献。与滑坡机制理解及前人研究一致，岩土属性被证实为关键且影响显著的因素（Intrieri and Gigli, 2016；Yan et al., 2019；Tang et al., 2020；Zhang et al., 2022b）。值得注意的是，形变测量值对预测准确性也有显著影响，强调考虑变量间相互作用对于提升预测能力的重要性。这一发现揭示了传统单点预测模型忽视关键变量依赖关系的潜在局限。降雨和水位作为次要贡献因子仍然重要，附录图A4显示水位始终显著影响预测准确度，该结论与观察到的水位变化周期模式相符。附录图A5进一步显示岩土属性对滑坡形变预测影响最大。

4.3. 白格滑坡的形变预测及影响因素解析

针对白格滑坡，我们探索了融合多源形变观测和领域知识的方法能否通过同时刻画整体系统行为及其局部复杂模式，实现滑坡形变预测。我们设计了三个逐步复杂的实验场景，输入数据逐渐丰富，包括时变环境变量、多方向形变和区域特定的地质知识。

在单目标预测场景ST-NSP-EV中，加入了代表关键影响因素的时变协变量，如海拔、坡度、湿度、温度和降雨，用于预测单一监测方向的形变时间序列。同时添加了其他监测点及方向的形变测量和坐标信息作为时变协变量。

在多目标预测场景MT-MPC中，利用多方向形变时间序列作为类别数据，并以监测点为额外类别标签，代表局部滑坡状况。

多目标预测场景MT-MPC-PK-EV在MT-MPC基础上进一步整合了先验领域信息，包括形变数据的静态属性（如不稳定区域特征）和时变影响因素（海拔、温度、湿度、降雨等）。

4.3.1. 空间相关性在滑坡形变预测中的考虑

如图16所示，我们对三个不稳定区的预测误差指标进行了评估。环境预测因子与先验知识的整合（MT-MPC-PK-EV场景）显著提升了预测精度，尤其是在K2和K3区域。然而在K1区，此信息的加入反而降低了预测精度，表明不同滑坡区域的预测来源存在异质性（Intrieri and Gigli, 2016）。

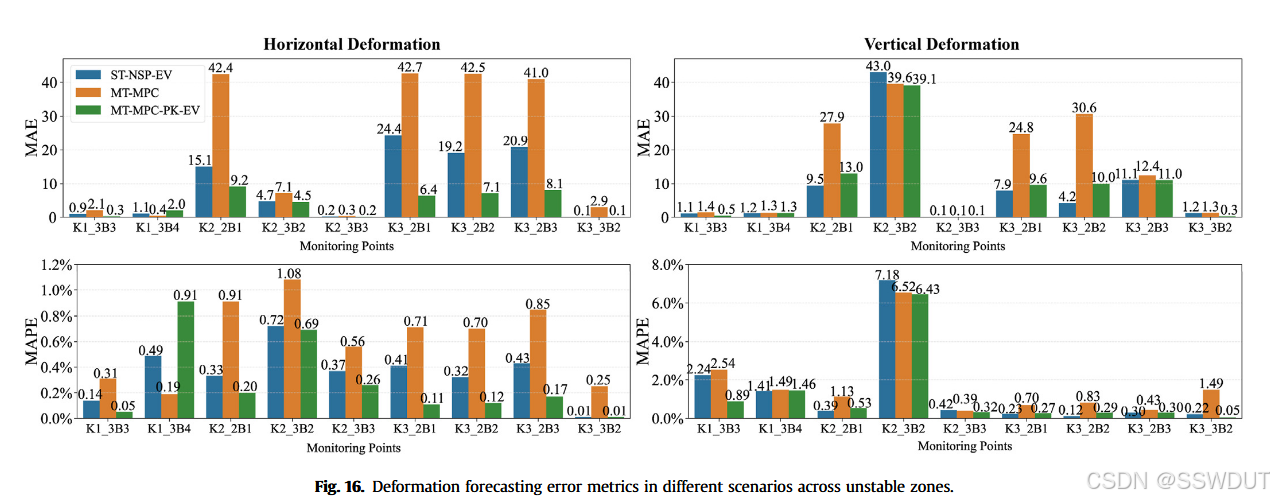
随后，我们考察了方法对滑坡水平方向与垂直方向形变的预测结果。与预期一致，整合多种环境预测因子和空间相关先验知识显著提升了复杂滑坡现象的预测能力。图17中灰线代表神经网络对滑坡时间特征的时间敏感度，显示知识融合的深度网络在预测时对当前时刻赋予高度权重。监测点K1与K3（滑坡右侧）时间滞后五步的明显峰值，暗示滑坡在接下来6天可能维持稳定，但长周期内存在较大位移风险。

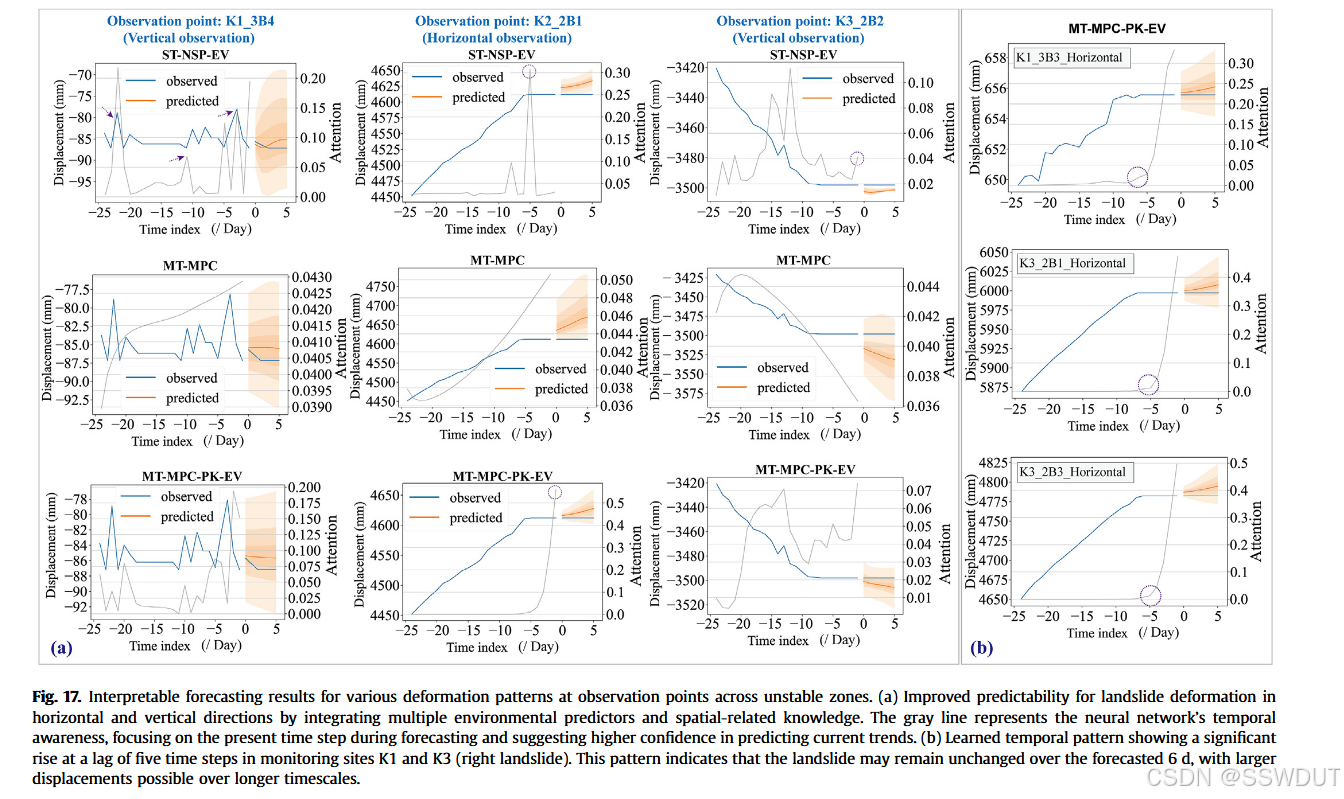
4.3.2. 滑坡形变预测中关键影响因素的识别

在白格滑坡案例中，我们使用方法定量评估了各预测因子的贡献及影响，识别出显著提升滑坡形变预测的关键因子。基于可解释深度学习，首次揭示了白格滑坡复杂的时空动力学。图18a展示ST-NSP-EV场景下预测因子对不同滑坡区的异质贡献。在K2和K3等区，降雨被视为关键的预测来源，可能与渗流机制相关（Li et al., 2019, 2020a）；而温度主导K1区，或因其对雪融和孔隙水压力的影响（Su et al., 2019；Zhang et al., 2020）。MT-MPC-PK-EV场景强调降雨作为滑坡预测的重要因素（见图18c）。

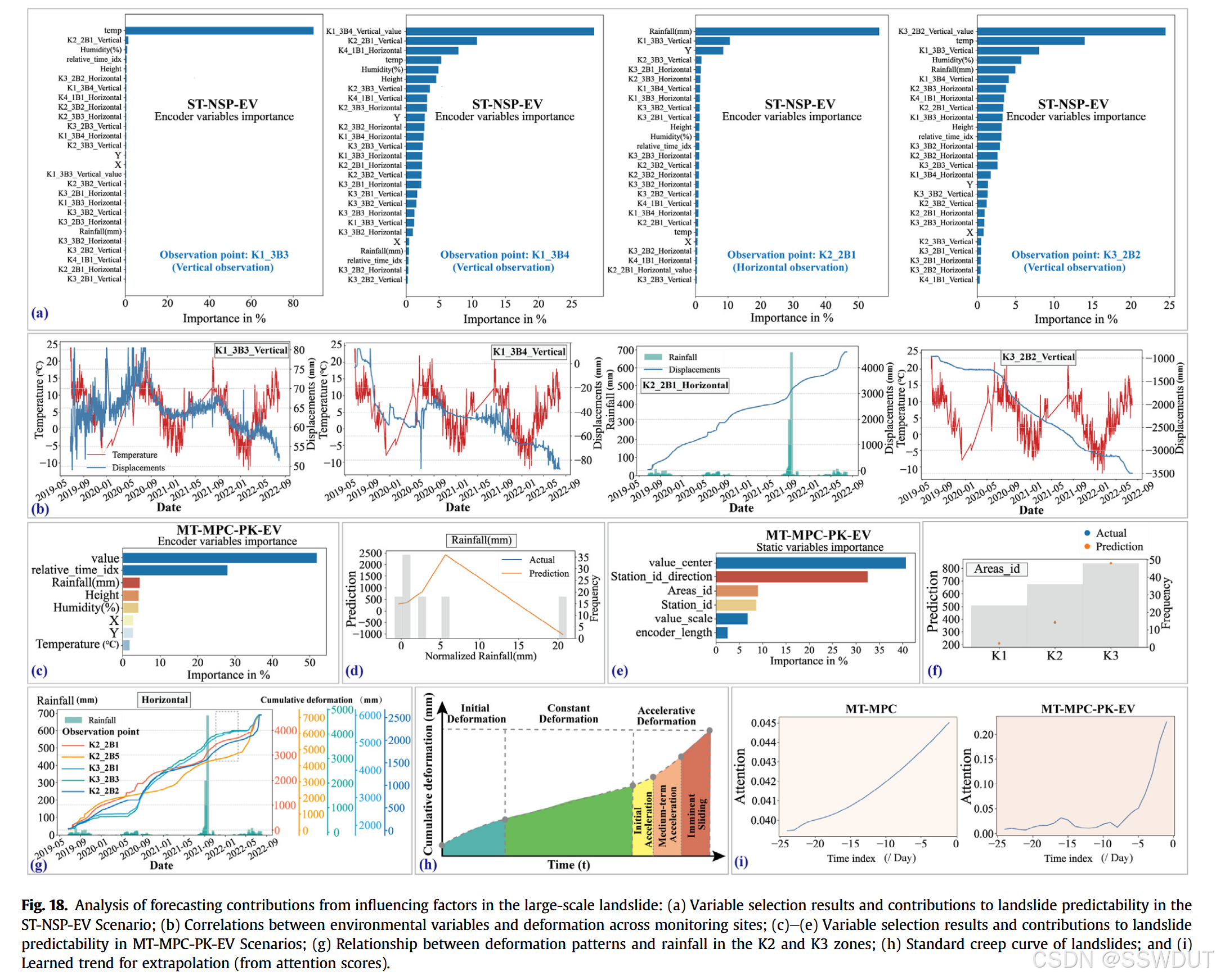
这些结果明确显示影响滑坡的因素在不同滑坡区域表现不同，强调在预测中必须考虑空间异质性。此外，两种场景提取的时间特征均表现出加速增长趋势（图18a），对应标准蠕变曲线的第三阶段，即形变速率逐渐增加（Li et al., 2020b）。在白格滑坡背景下，这意味着经历了相对稳定期后，长时间尺度内可能出现显著位移。尽管未发现直接可比的层次分析法（AHP）研究，整体因子排序与既有研究和滑坡驱动机制相符，进一步验证了本研究发现的有效性。附录图A10提供了支持性结果。

5. 讨论

本研究提出了一种全面的滑坡形变预测方法，兼顾该类现象的时空特征。基于多点形变观测，我们融合了可解释深度学习技术与详细领域知识，提供比传统方法更具洞察力和实用性的预测结果。

从空间角度看，该方法能够捕捉多个观测点间形变模式的传播和相互依赖，揭示整个滑坡系统的整体行为。此前较少关注的复杂相互依赖网络，有助于更好地理解不同区域滑坡运动的传播与同步，最终促进对整体形变行为的深入分析。

从时间角度看，结合区域特定领域知识，方法识别出每一区域独特的时间演化模式，整合内在属性与外部触发因素，实现整体趋势和幅度的预测，同时揭示不同区块对多种触发因素的响应差异。

接下来，我们将从三个关键视角讨论提出的集成且可解释的深度学习滑坡形变预测方法：

1. 深度学习与领域知识整合对滑坡预测性能的显著提升；

2. 基于可解释深度学习获得的主要发现及其意义；

3. 当前方法的局限性及未来在多样滑坡类型和环境中的更广泛适用性。

5.1. 深度学习与领域知识整合对滑坡形变预测的显著提升

现有滑坡形变预测方法常难以有效处理复杂的时空动力学。我们提出的创新方法通过将领域知识与可解释深度学习结合，显著提升了滑坡形变的预测能力。

具体而言，本方法通过以下三方面实现性能提升：

1. 利用多点监测数据刻画滑坡的时空行为；

2. 融入区域特定领域知识，实现对局部特征的深入理解；

3. 数据与知识的融合，获得全面的形变洞察。

首先，基于多点形变数据，我们将滑坡视为由多个相互影响的离散斑块组成的网络，识别整体滑坡系统行为（Lim et al., 2021）。类似假设认为，特定监测点观测可作为滑坡系统中对应斑块的代理指标（Handwerger et al., 2022）。这些观测间的关系反映斑块间的相互连接。

具备增强空间感知能力的深度神经网络能有效识别部分监测点出现的异常情形。例如，在滑坡灾变前，多个监测点形变显著增加，深度神经网络能结合斑块间的相互作用，精准发现相对稳定区域的突变信号。

其次，针对每个监测点的局部环境和条件进一步考虑差异化响应。我们将描述每个观测点地理环境的属性视为先验知识，通常为定性描述。已有研究表明，词嵌入技术可将文本信息映射至高维空间，有效捕获复杂的地质属性关系（Padarian and Fuentes, 2019；Lawley et al., 2022）。受此启发，我们利用每个监测点周边的定性描述作为先验知识，通过词嵌入编码，增强局部预测能力。

第三，关键在于无缝融合数据与领域知识。我们设计了基于Transformer的神经网络架构，从多点监测数据中提取复杂关系。在嵌入的领域知识引导下，网络采用门控机制筛选关键特征，弥补传统方法可能忽略的信息。同时，基于LSTM的模块结合领域知识，丰富对滑坡局部时序行为的理解。

5.2. 通过可解释深度学习洞察获得的主要发现

本研究通过可解释深度学习提取关键洞察，深化了对滑坡形变预测的理解。我们的研究聚焦于两个核心方面：（1）识别滑坡形变的主要驱动因素；（2）揭示这些因素影响下的时空动态。通过真实案例验证了方法的有效性，证明其在预测过程中能够提供对滑坡形变动力学的深入洞察。

在黄连树滑坡案例中，我们发现该水库滑坡前缘的周期性形变模式与水位波动高度相关。通过对比预测变量（水位）与学习到的形变时间模式，证明将先验知识注入可解释神经网络能够捕捉并展示与水库滑坡相关的关键物理过程。这一发现表明，实时水位监测在水库滑坡预警系统中可能发挥重要作用。

在白格滑坡案例中，我们识别出降雨和温度在驱动该缓慢蠕动滑坡不同区域快速形变中的关键作用。同时考虑不稳定区域的分类也有助于提升预测能力，因为不同区域展现出独特的裂缝分布和岩性特征。形变外推的时间模式显示未来形变呈快速增长趋势，该观察结果通过三个月后滑坡的实际崩塌得到验证。

5.3. 局限性与适用性

本研究存在两个值得进一步探讨的局限性。首先，当前方法主要依赖领域知识进行空间识别，尽管能有效捕捉不同滑坡区的异质性，但难以显式刻画控制滑坡形变的复杂物理过程。其次，本研究仅在有限的滑坡类型上验证模型，尚未充分探索其在更广泛情形中的适用性。

未来计划针对上述两点进行改进：

1. 计划通过引入基于物理过程的模型来增强所提综合框架。该步骤包括将已建立的滑坡力学物理模型（如水文模型和岩土力学模型）嵌入深度学习架构中。通过在架构中融合物理定律和约束，期望模型能更细致地刻画和理解滑坡动力学。

2. 拟拓展方法适用范围，涵盖更多滑坡类型，如地震诱发滑坡。多源数据融合支持整合地形、地震活动和材料属性等多种数据。地震诱发滑坡通常受地形崎岖度指数、坡度、断层线距离、峰值地面加速度和破裂区距离等因素影响（Tanyas et al., 2019；Gong et al., 2023；Pyakurel et al., 2023）。预计这些数据将为地震诱发滑坡预测提供宝贵输入。

此外，方法有望揭示这些因素的贡献，明确它们对地震诱发滑坡形变模式的潜在影响。可解释方法预计能刻画这些时变形变模式，并识别地震导致的滑坡行为突变与加速（Sun and Huang, 2023；Zhang et al., 2023b）。

鉴于当前数据样本量的限制，未来将扩展数据采集。现有数据虽足以进行初步验证，但为全面探讨和验证（尤其是地震诱发滑坡情形），仍需更多样化和大规模数据。

总之，所提综合且可解释的深度学习方法在区域尺度滑坡预警系统中展现出巨大潜力，有助于提升公共安全和基础设施韧性。该方法关键在于揭示滑坡类型与影响因素之间复杂交互关系，揭示每种触发机制的特定时空模式，从而实现快速且针对性的滑坡预警。

6. 结论

本文提出了一种新颖的滑坡形变预测方法，该方法将领域知识融入可解释深度学习，考虑时空相关性。通过捕捉和揭示内外因素作用下的滑坡形变模式，提升了预测准确性并明确了预测来源。

主要贡献和发现如下：

• 本方法从两个方面推动滑坡形变预测发展。首先，融合来自不同监测点的多组形变测量数据，并整合各监测点的领域知识，捕捉整体复杂形变模式，同时考虑各点时间模式的异质性。整体视角有助于捕捉外部因素对不同区域的异质影响，从而显著提升预测精度，优于现有方法。

• 其次，采用一种新颖的自解释神经网络，置于知识引导的深度学习框架中。该网络揭示了内外因素对形变预测的具体贡献，展示了用于外推未来形变的时间模式。方法不仅提升了预测能力，也揭示了提升预测的潜在机制。

在应用于黄连树水库滑坡和青藏高原白格滑坡两个案例中，得到若干重要发现：

• 黄连树滑坡案例中，方法有效识别水库水位波动为前缘形变的主要影响因素。捕获的时变周期模式与水位波动高度相关，体现了水库诱发滑坡的物理过程。

• 白格滑坡案例中，K1区形变主要受温度影响，K2与K3区形变主要受降雨影响，与观测数据分析结果一致。

这些发现表明，将领域知识融入可解释深度学习的滑坡形变预测方法具有显著的减灾潜力。