“鱼书”深度学习入门 笔记（1）前四章内容

最近在看斋藤康毅的《深度学习入门：基于Python的理论与实现》 ，以下按章节做一点笔记。
封面如下：（大家称为“鱼书”）

01 第二章 感知机

在本章中，可粗略将感知机理解为多输入，单输出的结构。

1.1 与门实现

# 01 AND 电路实现
def AND(x1, x2):w1, w2, theta = 0.5, 0.5, 0.7tmp = x1*w1 + x2*w2if tmp <= theta:return 0elif tmp > theta:return 1print(AND(0,0))
print(AND(0,1))
print(AND(1,0))
print(AND(1,1))# 优化版本
import numpy as np
def AND_1(x1, x2):x = np.array([x1, x2])w = np.array([0.5, 0.5])b = -0.7tmp = np.sum(w*x) + bif tmp <= 0:return 0else:return 1

与非门、或门等其他门，也可以用类似方法实现。
与门、与非门、或门是具有相同构造的感知机，区别只在于权重参数的值。

1.2 感知机的局限

将二输入或门平面化（形象化），可以得到如下图像：

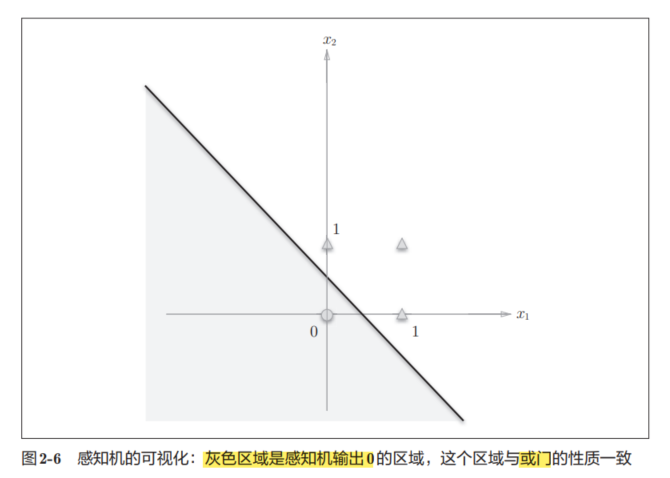
○表示0，△表示1。
如果想制作或门，需要用直线将图2-6中的○和△分开即可。
但观察异或门的平面化图像：

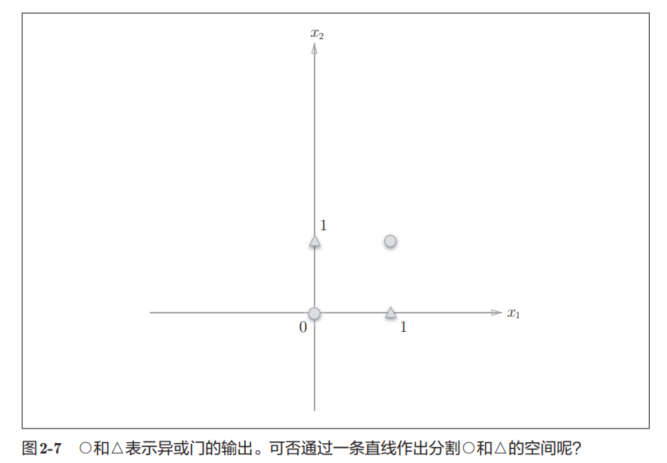
无法用一条直线将图2-7中的○和△分开，只能用曲线将其分开，需要用曲线分割而成的空间称为非线性空间。
感知机的局限性就在于它只能表示由一条直线分割的空间。

1.3 多层感知机

感知机的绝妙之处在于它可以“叠加层”。
我们可以通过能够实现的单层感知机，构成异或门，如图2-11所示。

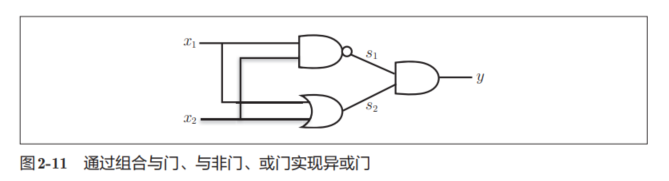
即，使用之前定义的AND函数、NAND函数、OR函数实现异或门。

def XOR(x1, x2):s1 = NAND(x1, x2) s2 = OR(x1, x2)y = AND(s1, s2)return y

所以，我们可以很容易明白，感知机可以通过叠加层进行非线性的表示。

02 第三章 神经网络

感知机是神经网络的基础。
理论上，复杂的计算，也是可以通过感知机表达出来，但是确定符合预期的参数，往往是由人工确定的。而神经网络比较重要的一个性质，就是它可以自动地从数据中学习到合适的权重参数。

2.1 基本结构

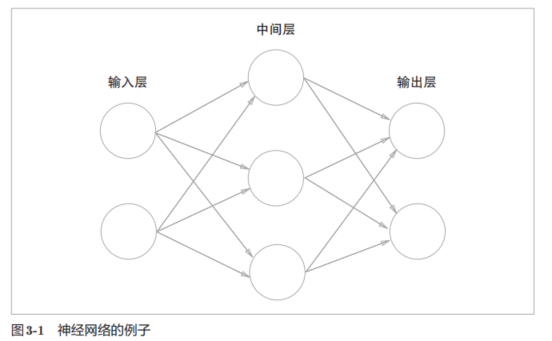
如下图为基本结构，中间层也叫隐含层。
由于参数（权重）设置只有两层，所以被称为两层网络。

2.2 激活函数

2.2.1 基本理解

激活函数的作用在于决定如何来激活输入信号的总和。
对于某一个输出，设有：
a = b + w1x1 + w2x2
y = h(a)
过程可以用下图理解，神经元的○中明确显示了激活函数的计算过程，即信号的加权总和为节点a，然后节点a被激活函数h()转换成节点y。

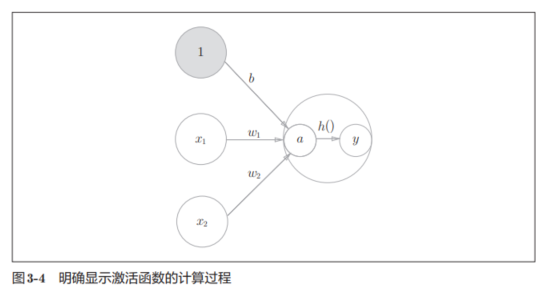
2.2.2 常用激活函数

sigmoid函数表达式：

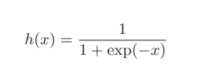
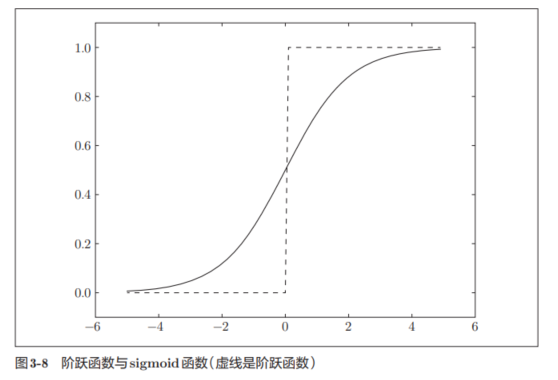
sigmoid函数如下，可以粗略看看与阶跃函数的对比：
两者的区别主要在平滑性和返回值上

ReLU函数：
表达式为：

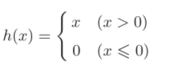
函数图像为：

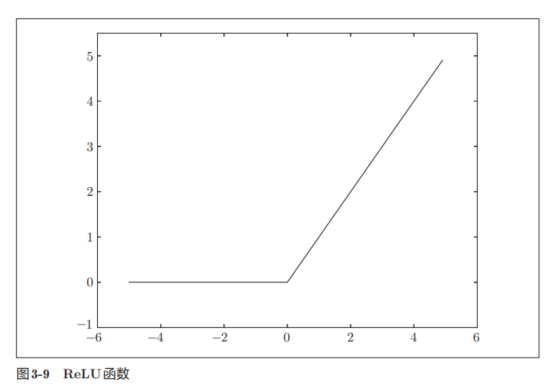
ReLU的函数实现非常简单，maximum函数会从输入的数值中选择较大的那个值进行输出：

import numpy as npdef relu(x):return np.maximum(0, x)

一般地，回归问题可以使用恒等函数，二元分类问题可以使用sigmoid函数，多元分类问题可以使用softmax函数。
softmax的计算式为，计算值表示属于某一类的概率：

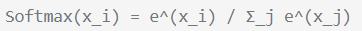
但是softmax函数存在溢出风险，因为指数运算很容易让值变得很大。
改进方式如下：

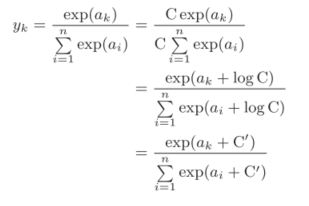
理论上，这里的C '可以使用任何值，但是为了防止溢出，一般会使用输入信号中的最大值。下面给出一个例子：

如上，就可以防止溢出问题。整理代码实现softmax函数：

def softmax(a):c = np.max(a)exp_a = np.exp(a - c) # 溢出对策 sum_exp_a = np.sum(exp_a)y = exp_a / sum_exp_areturn y

2.2.3 符号定义

基本规则如下图：

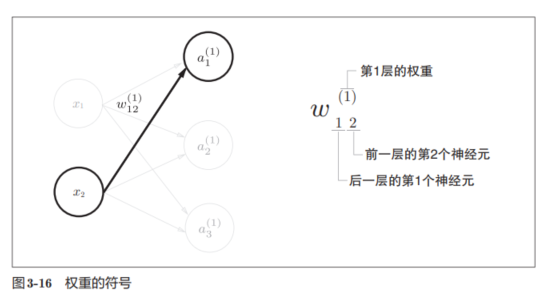
下面是一个完整的表达：


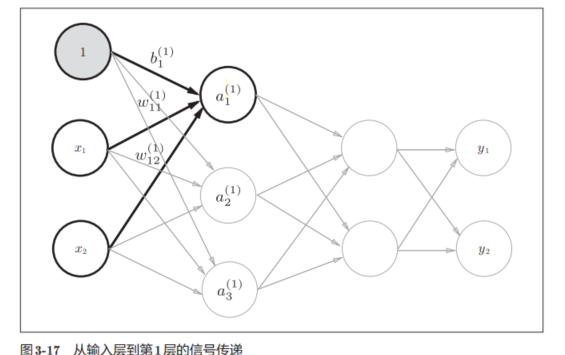
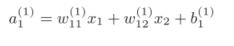
所以，考虑到矩阵的乘法运算，可以将第1层的加权和表示如下，进行数组计算时一定要注意维度的问题：

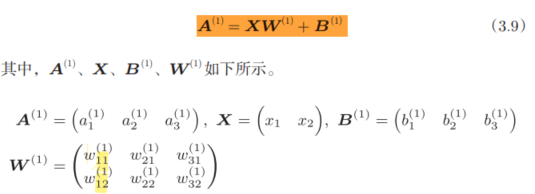
对于分类问题，输出层的神经元数量一般设定为类别的数量。

2.2.4 其他概念

把数据限定到某个范围内的处理称为正规化（normalization）。
对神经网络的输入数据进行某种既定的转换称为预处理（pre-processing）。
实际上，很多预处理都会考虑到数据的整体分布。比如，利用数据整体的均值或标准差，移动数据，使数据整体以0为中心分布，或者进行正规化，把数据的延展控制在一定范围内。
除此之外，还有将数据整体的分布形状均匀化的方法，即数据白化（whitening）等。
打包式的输入数据称为批（batch）。批处理可以加快运算，本书的解释如下：

03 第四章 神经网络的学习

本章所说的“学习”是指从训练数据中自动获取最优权重参数的过程。
为了使神经网络能进行学习，引入损失函数这一指标。学习的目的就是以该损失函数为基准，找出能使它的值达到最小的权重参数。
为了找出尽可能小的损失函数的值，引入梯度。

本章用Python实现对MNIST手写数字数据集的学习。
（代码部分不完全是作者提供的，按自己习惯的方式进行了部分修改，逻辑基本相差不大）

3.1 数据

如果让我们自己来设计一个能将数字5正确分类的程序，这非常难，一方面，我们难以归纳出我们是基于什么规则进行识别的；另一方面，每个人，都有不同的写字习惯。

• 一种方案，从图像中提取特征量，利用“机器学习”学习这些特征量的模式。

图像的特征量通常表示为向量的形式。
在计算机视觉领域，常用的特征提取方法包括SIFT、SURF和HOG等。使用这些特征量将图像数据转换为向量，然后对转换后的向量使用SVM、KNN等分类器进行学习。
贴上gpt对这三种特征提取方法的基本介绍：




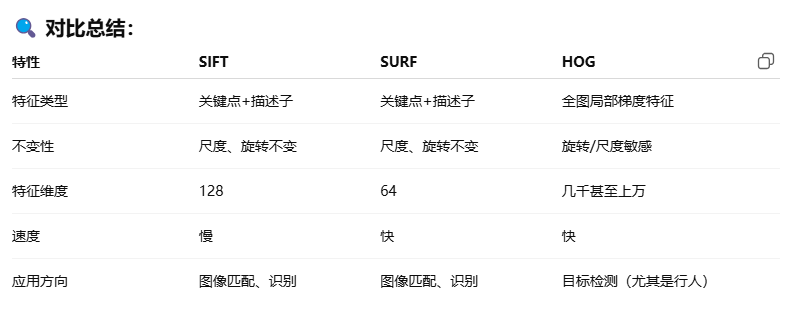
可以等后面有需要了，再详细学习算法逻辑。
因为不同场景适合于不同的特征向量，这里需要用到的特征向量提取的方法，还是需要人为比较（人为介入）。而深度学习（神经网络）被认为尽量少人为介入的方法。
即，神经网络的优点是对所有的问题都可以用同样的流程来解决。比如，不管要求解的问题是识别5，还是识别狗，抑或是识别人脸，神经网络都是通过不断地学习所提供的数据，尝试发现待求解的问题的模式。

3.1.1 训练数据和测试数据

一般将数据分为训练数据和测试数据两部分来进行学习和实验等。
首先，使用训练数据进行学习，寻找最优的参数；然后，使用测试数据评价训练得到的模型的实际能力。
即，测试集，为了正确评价模型的泛化能力（适用于不同数据集的能力）。

3.1.2 过拟合

对某个数据集过度拟合的状态称为过拟合（over fftting）。

3.2 损失函数

神经网络以某个指标为线索寻找最优权重参数。神经网络的学习中所用的指标称为损失函数（loss function）。
这个损失函数可以使用任意函数，但一般用均方误差和交叉熵误差等。

3.2.1 均方误差

均方误差的表达式为：

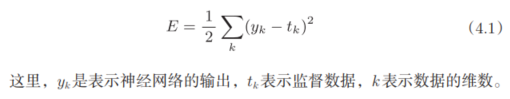
3.2.2 交叉熵误差

交叉熵误差的关系式为：

即，交叉熵误差的值是由正确解标签所对应的输出结果决定的。

3.2.3 mini-batch学习

神经网络的学习往往是从训练数据中选出一批数据（称为mini-batch,小批量），然后对每个mini-batch进行学习。比如，从60000个训练数据中随机选择100笔，再用这100笔数据进行学习。这种学习方式称为mini-batch学习。

先读取数据集：

import torch
import numpy as np
from torchvision import datasets,transforms
import torch.nn.functional as F# 所有图像和标签打包到 DataLoader 中
from torch.utils.data import DataLoader# 这行代码会自动下载并加载 MNIST 数据集
mnist_train = datasets.MNIST(root='./data_mnist', train=True, download=True,transform= transforms.ToTensor())
mnist_test = datasets.MNIST(root='./data_mnist', train=False , download=True,transform= transforms.ToTensor())train_loader = DataLoader(mnist_train, batch_size=len(mnist_train))  # 一次性全部取出
images_train, labels_train = next(iter(train_loader))
test_loader = DataLoader(mnist_test, batch_size=len(mnist_test))  # 一次性全部取出
images_test, labels_test = next(iter(test_loader))# 手动将标签转换为 One-Hot 编码
# F.one_hot 默认输出 LongTensor，我们转成 float32 方便后续计算
labels_train_one_hot = F.one_hot(labels_train, num_classes=10).float()
labels_test_one_hot = F.one_hot(labels_test, num_classes=10).float()
# 变成二维张量
images_train=np.reshape(images_train,(60000,784))
images_test=np.reshape(images_test,(10000,784))# 输出各个数据的形状
print(f"图像 shape: {images_train.shape}")
print(f"标签 shape: {labels_train.shape}")
print(f"标签（One-Hot） shape: {labels_train_one_hot.shape}")  # torch.Size([60000, 10])
print('ok')

这里标签转换成了one-hot label的形式。（即仅正确解标签为1，其余为0的数据结构）。
尝试从这个训练数据中随机抽取10笔数据，使用NumPy的np.random.choice()，部分代码如下：

# 训练数据随机抽出10笔数据
train_size=len(images_train)  #len() 返回的是张量的第一个维度（axis=0）的大小
test_size=len(images_test)
bact_size=10
# 从 train_size 个样本中随机选出 batch_size 个重复的索引，存入 batch_mask
batch_mask=np.random.choice(train_size,bact_size)  #replace参数默认为true，表示可以重复的索引
images_train_batch=images_train[batch_mask]
labels_train_batch=labels_train_one_hot[batch_mask]print(batch_mask)
print(images_train_batch.shape)

可以适当设置print，查看代码是否实现了需求。
后续只需指定这些随机选出的索引，取出mini-batch，使用这个mini-batch计算损失函数即可。

3.2.4 mini-batch版交叉熵误差的实现

交叉熵的计算包括one-hot标签和非one-hot标签两种。
下面贴上gpt贴上的介绍和对比。

如果是正常运算的情况下，对于同一组数据，one-hot标签和非one-hot标签的运算结果是一致的。

下面是这部分代码：

# 计算mini-batch交叉熵误差
# 配合one-hot 编码的标签
# y表示模型的预测输出（通常是softmax输出，值在0-1之间），t表示真实标签（通常是one-hot编码的形式）
def cross_entropy_error(y, t):if y.ndim == 1:  # 如果y是一维向量（即单个样本），则对其进行维度扩展，变成二维的形状t = t.reshape(1, t.size)y = y.reshape(1, y.size)batch_size = y.shape[0]  #batch_size表示一个batch中样本的数量return -np.sum(t * np.log(y + 1e-7)) / batch_size

贴一点最后一句的分步解释：

如果是非one-hot方法，最后一句话发生变化，变成：
-np.sum(np.log(y[np.arange(batch_size), t] + 1e-7))/ batch_size
其中，y[np.arange(batch_size), t] 表示从每一行 y[i] 中，选出 t[i] 所对应的那个元素。
下面给出一简单例子：

3.2.5 为什么要设定损失函数

损失函数也可以叫目标函数（objective function） 或 代价函数（cost function），本质上衡量模型好坏的。

“在进行神经网络的学习时，不能将识别精度作为指标。因为如果以识别精度为指标，则参数的导数在绝大多数地方都会变为 0。”
如何理解？
识别精度（accuracy）是一个离散型指标，只告诉我们：
预测结果是否正确（1 或 0），举例：
预测正确 → accuracy = 1；预测错误 → accuracy = 0

可以清楚：

• accuracy 是一个“非连续”、“不光滑”的函数（同理，阶跃函数也存在绝大多数时候导数为0，导致微小变化被抹杀）
• 它不像交叉熵那样随着输出概率的细微变化连续变化
• 它在“预测是否正确”这一个点上突然跳变 → 不可导！

一般说的最优参数是指损失函数取最小值时的参数（理论上）。
使用梯度来寻找函数最小值（或者尽可能小的值）
梯度表示的是各点处的函数值减小最多的方向
（在复杂的函数中，梯度指示的方向基本上都不是函数值最小处，还可能是极小值或鞍点，也可能是学习的平坦期）

3.3 梯度

寻找最小值的梯度法称为梯度下降法（gradient descent method），寻找最大值的梯度法称为梯度上升法（gradient ascent method）。
通过反转损失函数的符号，求最小值的问题和求最大值的问题会变成相同的问题

参数更新的定义为：

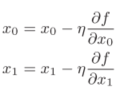
η叫学习率，决定在一次学习中，应该学习多少，以及在多大程度上更新参数。
若有更多的变量，更新表达式与上类似。
学习率需要事先确定数值，一般会一边改变学习率的值，一边确认学习是否正确进行了。在一些算法中，也提出在不同位置，学习率会进行变化。

使用随机选择的mini batch数据，随机梯度下降法（stochastic gradient descent）简写为SGD。

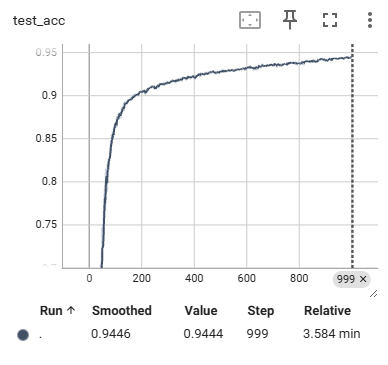
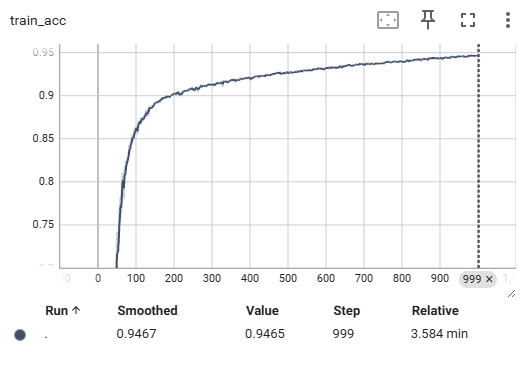
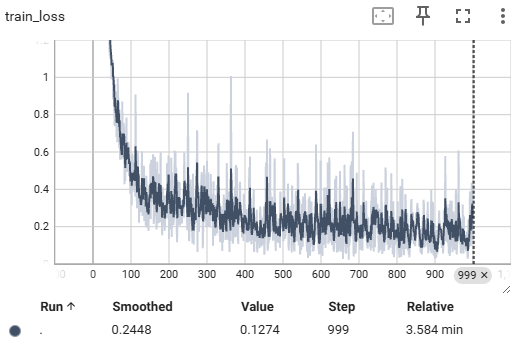
组合起来，一个完整代码，主要用tensorboard进行展示。
还是会有比较多可优化的地方，这里主要和书上逻辑一致（比如，很多函数都自己写的，实际可以直接调用）。超参数设置比较大的时候，需要跑的时间比较久，可以先改成比较小的值，先看功能可不可以实现，再说其他。

# 03 实现两层神经网络
import sys, os
import numpy as np
from torch.utils.tensorboard import SummaryWriter# 函数定义
def identity_function(x):return xdef step_function(x):return np.array(x > 0, dtype=np.int)def sigmoid(x):return 1 / (1 + np.exp(-x))def sigmoid_grad(x):return (1.0 - sigmoid(x)) * sigmoid(x)def relu(x):return np.maximum(0, x)def relu_grad(x):grad = np.zeros(x)grad[x >= 0] = 1return graddef softmax(x):if x.ndim == 2:x = x.Tx = x - np.max(x, axis=0)y = np.exp(x) / np.sum(np.exp(x), axis=0)return y.Tx = x - np.max(x)  # 溢出对策return np.exp(x) / np.sum(np.exp(x))def mean_squared_error(y, t):return 0.5 * np.sum((y - t) ** 2)def cross_entropy_error(y, t):  # 交叉熵损失if y.ndim == 1:t = t.reshape(1, t.size)y = y.reshape(1, y.size)# 监督数据是one-hot-vector的情况下，转换为正确解标签的索引if t.size == y.size:t = t.argmax(axis=1)batch_size = y.shape[0]return -np.sum(np.log(y[np.arange(batch_size), t] + 1e-7)) / batch_sizedef softmax_loss(X, t):y = softmax(X)return cross_entropy_error(y, t)# 梯度计算
def numerical_gradient(f, x):h = 1e-4  # 0.0001grad = np.zeros_like(x)# 创建nditer迭代器# nditer 常用于在多维数组上高效地逐元素访问、修改等操作# flags=['multi_index']表示可以获取当前元素在多维数组中的坐标索引# op_flags=['readwrite']，表示X中的元素可读可写it = np.nditer(x, flags=['multi_index'], op_flags=['readwrite'])while not it.finished:  # it.finished 是一个布尔值，表示是否迭代完成idx = it.multi_index  # 获取当前索引tmp_val = x[idx]  # 取出当前值x[idx] = float(tmp_val) + hfxh1 = f(x)  # f(x+h)x[idx] = tmp_val - hfxh2 = f(x)  # f(x-h)grad[idx] = (fxh1 - fxh2) / (2 * h)  # 用中心差分公式计算梯度x[idx] = tmp_val  # 还原值，确保不会影响后续计算it.iternext()  #移动到下一个元素，继续循环return gradclass TwoLayerNet:def __init__(self, input_size, hidden_size, output_size, weight_init_std=0.01):# 初始化权重self.params = {}self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size)self.params['b1'] = np.zeros(hidden_size)self.params['W2'] = weight_init_std * np.random.randn(hidden_size, output_size)self.params['b2'] = np.zeros(output_size)def predict(self, x):W1, W2 = self.params['W1'], self.params['W2']b1, b2 = self.params['b1'], self.params['b2']a1 = np.dot(x, W1) + b1z1 = sigmoid(a1)a2 = np.dot(z1, W2) + b2y = softmax(a2)return y# x:输入数据, t:监督数据def loss(self, x, t):y = self.predict(x)return cross_entropy_error(y, t)def accuracy(self, x, t):y = self.predict(x)y = np.argmax(y, axis=1)t = np.argmax(t, axis=1)accuracy = np.sum(y == t) / float(x.shape[0])return accuracy# x:输入数据, t:监督数据def numerical_gradient(self, x, t):loss_W = lambda W: self.loss(x, t)grads = {}grads['W1'] = numerical_gradient(loss_W, self.params['W1'])  # 计算梯度值（计算损失函数分别对权重参数的偏导）grads['b1'] = numerical_gradient(loss_W, self.params['b1'])grads['W2'] = numerical_gradient(loss_W, self.params['W2'])grads['b2'] = numerical_gradient(loss_W, self.params['b2'])return gradsdef gradient(self, x, t):W1, W2 = self.params['W1'], self.params['W2']b1, b2 = self.params['b1'], self.params['b2']grads = {}batch_num = x.shape[0]# forwarda1 = np.dot(x, W1) + b1z1 = sigmoid(a1)a2 = np.dot(z1, W2) + b2y = softmax(a2)# backwarddy = (y - t) / batch_num   # 计算的是平均交叉熵grads['W2'] = np.dot(z1.T, dy)  #计算的是L对W2的梯度，下面同理grads['b2'] = np.sum(dy, axis=0)da1 = np.dot(dy, W2.T)dz1 = sigmoid_grad(a1) * da1grads['W1'] = np.dot(x.T, dz1)grads['b1'] = np.sum(dz1, axis=0)return grads# mini-batch实现
from torchvision import datasets,transforms
import torch.nn.functional as F# 所有图像和标签打包到 DataLoader 中
from torch.utils.data import DataLoader# 这行代码会自动下载并加载 MNIST 数据集
mnist_train = datasets.MNIST(root='./data_mnist', train=True, download=True,transform= transforms.ToTensor())
mnist_test = datasets.MNIST(root='./data_mnist', train=False , download=True,transform= transforms.ToTensor())# 分离
train_loader = DataLoader(mnist_train, batch_size=len(mnist_train))  # 一次性全部取出
images_train, labels_train = next(iter(train_loader))
test_loader = DataLoader(mnist_test, batch_size=len(mnist_test))  # 一次性全部取出
images_test, labels_test = next(iter(test_loader))# 手动将标签转换为 One-Hot 编码
# F.one_hot 默认输出 LongTensor，我们转成 float32 方便后续计算
labels_train_one_hot = F.one_hot(labels_train, num_classes=10).float()
labels_test_one_hot = F.one_hot(labels_test, num_classes=10).float()
# 变成二维张量
# 之前版本没有加.numpy()，会报错，因为np.reshape和tensor的结构混乱了，需要改为一致
images_train=np.reshape(images_train.numpy(),(60000,784))
images_test=np.reshape(images_test.numpy(),(10000,784))
labels_train=np.reshape(labels_train_one_hot.numpy(),(60000,10))
labels_test=np.reshape(labels_test_one_hot.numpy(),(10000,10))# rename here
# x means imgs, t means labels
x_train,t_train=images_train,labels_train
x_test,t_test=images_test,labels_testtrain_loss_list = []
train_acc_list = []
test_acc_list = []# 超参数
iters_num = 10000
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.1network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)
writer=SummaryWriter('logs_book')step=0
for i in range(iters_num):# 获取mini-batchbatch_mask = np.random.choice(train_size, batch_size)x_batch = x_train[batch_mask]t_batch = t_train[batch_mask]# 计算梯度# grad = network.numerical_gradient(x_batch, t_batch)grad = network.gradient(x_batch, t_batch) # 高速版! # 更新参数，推荐使用这个for key in ('W1', 'b1', 'W2', 'b2'):network.params[key] -= learning_rate * grad[key]# 记录学习过程loss = network.loss(x_batch, t_batch)train_loss_list.append(loss)# 每10次记录一次精度if i % 10 == 0:train_acc = network.accuracy(x_train, t_train)test_acc = network.accuracy(x_test, t_test)train_acc_list.append(train_acc)test_acc_list.append(test_acc)print("train acc, test acc | " + str(train_acc) + ", " + str(test_acc))writer.add_scalar("train_acc", train_acc, step)writer.add_scalar("test_acc", test_acc, step)writer.add_scalar("train_loss", loss, step)step += 1# 监控迭代到哪里了if i % 5==0:print(i)writer.close()

我修改了一下参数，让尽量快一点迭代，结果可以看到一些结果图，比较符合预期：