如何验证分类模型输出概率P值的“好坏”:评估与校准示例
在分类建模中,除了常见的准确率、AUC、召回率等指标外,模型输出的概率值是否真实可信(即概率校准),是评估模型质量的重要维度。
本文结合 Samuele Mazzanti 在 Medium 上的文章,系统讲解如何验证模型预测概率的质量,介绍衡量指标 Expected Calibration Error (ECE) 及其合理基线的确定方法,并提供实用代码示例。
文章:
How to Test if Your Model’s Probabilities Are Good (Enough)
关联代码github:medium_how_to_test_if_your_model_probabilities_are_good_enough
内容大纲:
| 关键点 | 说明 |
|---|---|
| 验证模型概率质量 | 通过分箱校准曲线比较预测概率与真实正样本比例 |
| 衡量指标 ECE | 量化预测概率与真实概率的平均偏差 |
| 合理基线判断 ECE 好坏 | 设计统计基线,计算 p 值,判断模型概率是否显著优于随机概率 |
| 校准器作用与检查方法 | 用辅助模型调整概率分布,校准前后比较 ECE 和校准曲线有效性 |
文章目录
- 1. 模型输出概率的质量如何验证?
- 1.1 分箱校准曲线
- 1.2 衡量预测概率与真实分布差异的指标:Expected Calibration Error (ECE)
- 1.3 如何判断 ECE 是否“足够好”?
- 2 校准器(Calibrator)
- 2.1 校准器的作用
- 2.2 代码示例
1. 模型输出概率的质量如何验证?
1.1 分箱校准曲线
传统分类模型往往关注的是判别能力(如 ROC 曲线下的面积 AUC),即模型能否正确排序样本的正负概率。但在很多业务场景中,我们更关心模型输出的概率是否能真实反映事件发生的概率,例如金融风控、医疗诊断、营销推荐等。
再来看一个例子:
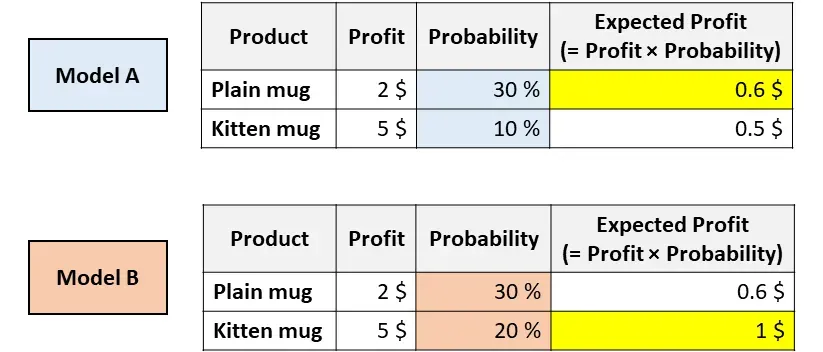
您的公司销售两个杯子——一个是纯白色的,另一个是小猫图案的。您需要通过预测顾客购买每个杯子的概率来决定向顾客展示哪个杯子。您训练了两个模型并得到了以上两个结果。
两种模型都认为用户更有可能购买普通的杯子(因此,模型 A 和模型 B 具有相同的 ROC 分数,因为该指标仅评估排序)。
然而,根据模型 A,根据 利润 * 概率,预期利润是普通杯子 > 小猫杯子,模型B 确相反。
所以,获得真实可靠的概率P值,也是非常重要的。
检验的方案:
- 基于“分箱校准曲线”(Calibration Curve):将测试集中预测概率相近的样本分为若干个区间(bin),计算每个区间内的平均预测概率和真实正样本比例。
- 如果模型概率是“真实概率”,那么每个分箱的平均预测概率应当接近该分箱内的真实正样本比例。
通过这种分箱比较,我们能直观地看到模型输出概率的偏差。
1.2 衡量预测概率与真实分布差异的指标:Expected Calibration Error (ECE)
为了量化校准曲线中预测概率与真实概率的偏差,文章定义了**预期校准误差(ECE)**指标。
ECE 定义
ECE=∑m=1M∣Bm∣n∣acc(Bm)−conf(Bm)∣ECE = \sum_{m=1}^M \frac{|B_m|}{n} \left| \text{acc}(B_m) - \text{conf}(B_m) \right|ECE=∑m=1Mn∣Bm∣∣acc(Bm)−conf(Bm)∣
- MMM:分箱数量
- BmB_mBm:第 mmm 个分箱的样本集合
- ∣Bm∣|B_m|∣Bm∣:第 mmm 个分箱样本数
- nnn:总样本数
- acc(Bm)\text{acc}(B_m)acc(Bm):第 mmm 个分箱内的真实正样本比例(准确率)
- conf(Bm)\text{conf}(B_m)conf(Bm):第 mmm 个分箱的平均预测概率(置信度)
作用
- ECE 反映了模型预测概率与实际概率的平均偏差。
- 值越小,说明模型概率越接近真实概率,校准效果越好。
1.3 如何判断 ECE 是否“足够好”?
ECE存在的问题:
- 箱子数量的选择是任意的:改变箱子数量将产生不同的 ECE 值 。
- 很难确定 ECE 值是否“足够好”。 虽然 ECE 值越低越好,但并没有明确的阈值来衡量可接受的值。就我们的情况而言,2.1% 是好还是坏?
所以需要寻找合理的基线
单纯看 ECE 数值难以判断模型概率是否合格,因为:
- 理想的 ECE 是 0,但实际上即使模型完美校准,也会因为随机性导致 ECE 不为零。
- 因此,直接用 0 作为基线不现实。需要一个实际的、基于随机波动的合理基线来对比。
文章提出的解决方案
- 设计一个合理的基线,用来对比当前模型的 ECE。
- 通过统计检验(如计算 p 值)判断模型的概率输出是否显著优于随机或不校准的概率分布。
- 只有当 ECE 明显低于基线时,才能认为模型概率“足够好”。
解决思路:反向模拟法
- 假设模型预测的概率是完美校准的,也就是说,模型给出的概率是真实的概率分布。
- 基于这些概率模拟多个目标变量:利用模型预测的概率,生成多组可能的“真实”标签(目标变量)。
具体做法是:
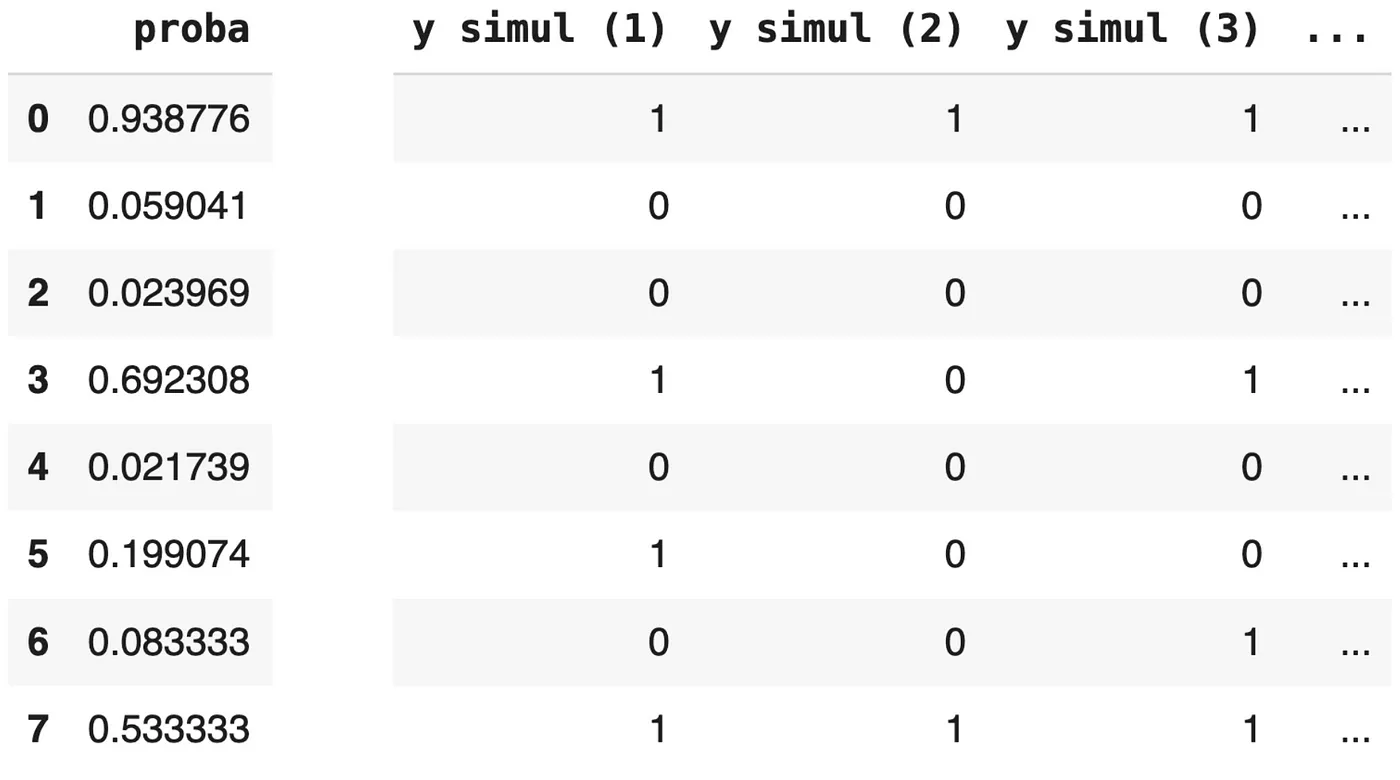
- 对每个样本,用预测概率作为事件发生的概率,随机生成 0 或 1 标签。
y_test_simul = np.random.uniform(0, 1, size=n) < proba_test这个模拟手法,笔者倒是疑惑了好一会,这里面会生成一个随机数,然后proba_test是模型预测概率 (proba_test):比如 0.9(即 90%),事件发生的可能性非常大。在这种情况下,大多数介于 0 到 1 之间生成的随机数都会小于 0.9,随机数如果落入(小于)0.9,就会标记为正例,为1
这种模拟方法能有效地将预测概率转化为模拟的二元结果,并且经过多次模拟后,模拟出的“1”的比例会与平均预测概率非常接近。
- 重复上述模拟过程多次(例如1000次),得到多个模拟的目标变量集合。
- 对每个模拟的目标变量,计算校准曲线和对应的 ECE。
- 构建 ECE 的分布基线,这些模拟的 ECE 代表在假设模型完美校准且存在随机波动情况下,可能出现的 ECE 范围。
- 比较实际模型的 ECE 与模拟分布,计算实际模型 ECE 在模拟 ECE 分布中的位置,类似于计算 p 值:
p_value = np.mean(simulated_eces >= actual_ece)
结果解释
- 如果 p 值很高(接近 1),说明实际模型的 ECE 在模拟的完美校准情况下也很常见,表明模型预测概率接近真实概率(校准较好)。
- 如果 p 值很低(接近 0),说明实际模型的 ECE 超出了完美校准情况下的随机波动范围,模型概率校准较差。
2 校准器(Calibrator)
校准器(Calibrator)如何帮助提升概率质量?如何检查校准器?
2.1 校准器的作用
校准器 是建模之后的一个“补充”模型
- 校准器是一个辅助模型,用来调整原始模型输出的概率分布,使其更接近真实概率。
- 常见方法有:
- 保序回归(Isotonic Regression):非参数单调函数拟合概率映射。
- Platt Scaling:用逻辑回归拟合概率映射。
校准器的训练流程
- 在验证集上获取原模型的预测概率。
- 用验证集的预测概率和真实标签训练校准器。
- 用校准器对测试集的预测概率进行转换,得到校准后的概率。
检查校准器的方法
- 同样使用分箱校准曲线和 ECE 指标,比较校准前后概率的校准效果。
- 校准后若 ECE 显著降低,说明校准器有效。
2.2 代码示例
我们要做的就是在验证集上训练我们的校准器:
from sklearn.isotonic import IsotonicRegressioncalibrator = IsotonicRegression(y_min = 0, y_max = 1, out_of_bounds = "clip")
proba_valid = model.predict_proba(X_valid)[:, 1]
calibrator = calibrator.fit(X=proba_valid, y=y_valid)
我们可以要求原始模型预测测试集上的分数,并使用校准器尝试纠正它们。
proba_test = model.predict_proba(X_test)[:, 1]cal_proba_test = calibrator.predict(proba_test)
最终的 ECE 和 p 值是多少。
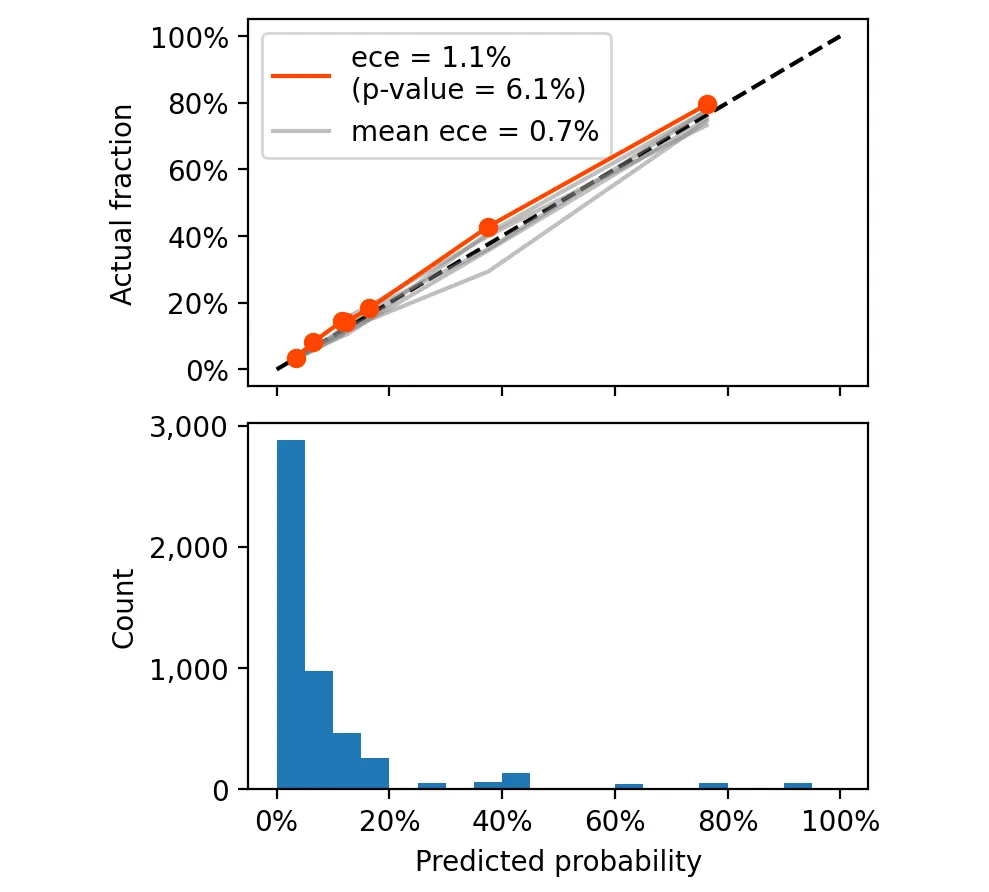
这次的 p 值为 6.1%,这意味着在 1,000 个完美校准的目标变量中,有 61 个的 ECE 大于或等于 1.1%。这表明,我们可以非常有信心,使用这个新模型可以得到真实的潜在概率。
