当前位置：首页 > news >正文

DFS习题篇【下】

news 2025/7/23 5:03:55

文章目录

P1683 入门
推荐练习
洪水灌溉
1114. 棋盘问题
P1025 数的划分

一些迷宫问题

P1683 入门

P1683 入门
在这里插入图片描述

这题考察的是最大联通问题，要把所有能走的瓷砖都走了才能通过。那么我们只需要弄清几个问题：

怎么走？怎么转弯？如何判断走还是不走等。
我们可以用dfs遍历，从@的位置开始，依次遍历它的四个方向，如果是 **.**就走，并ans++记录，同时为了避免重复计算还要再将它赋值为#.就这样一直搜下去，注意终止条件，代码中会有解释.

#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define int long long
#define PII pair<int,int>
#define fi first
#define se second
#define endl '\n'
const int N=26;
int n,m,ans; 
char a[N][N];
int dx[]={1,0,-1,0};
int dy[]={0,1,0,-1};
void dfs(int x,int y)
{if(x<1||x>n||y<1||y>m||a[x][y]=='#')//如果位置越界了，或者是#就返回掉 return ;a[x][y]='#';//赋值为#避免重复计算 ans++;//记录数量 for(int i=0;i<4;i++)//遍历四个方向 {int tx=x+dx[i];int ty=y+dy[i];dfs(tx,ty);}
}
void solve()
{cin>>m>>n;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){cin>>a[i][j];}	}for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){if(a[i][j]=='@')//从@的位置开始深搜 dfs(i,j);}	}cout<<ans;}
signed main()
{IOS;int _=1;
//	cin>>_;while(_--)solve();return 0;
}

洪水灌溉

P1596 [USACO10OCT] Lake Counting S

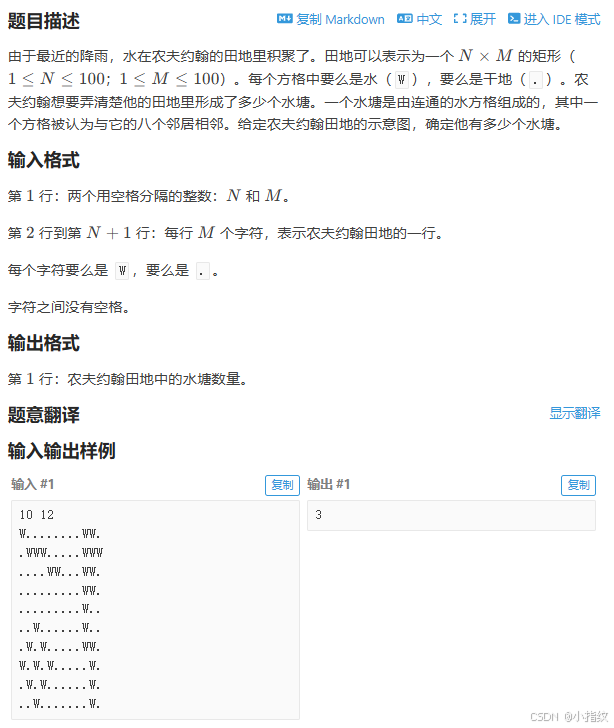
在这里插入图片描述

这道题是让找有几个连通块问题，我们只需先找到一个为W的点，再将它八个方向的点都深搜一下，将#改为.并且这一个联通部分只算一个水塘。这道题主要就是注意它的方向是八个方向，与以往的4的方向不同。
如果用方向数组写的话：(八联通）
int dx[]={1,1,1,0,0,-1,-1,-1}
int dy[]={-1,0,1,1,-1,1,0,-1}

#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define int long long
#define PII pair<int,int>
#define fi first
#define se second
#define endl '\n'
const int N=105;
int n,m,ans;
char a[N][N];
void dfs(int x,int y)
{if(x>n||x<1||y>m||y<1||a[x][y]=='.')return ;a[x][y]='.';dfs(x+1,y);dfs(x,y+1);dfs(x,y-1);dfs(x-1,y);dfs(x+1,y+1);dfs(x-1,y-1);dfs(x+1,y-1);dfs(x-1,y+1);} 
void solve()
{cin>>n>>m;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++)cin>>a[i][j];}for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){if(a[i][j]=='W'){ans++;
//				cout<<i<<" "<<j<<endl;dfs(i,j);}}}cout<<ans;
}
signed main()
{IOS;int _=1;
//	cin>>_;while(_--)solve();return 0;
}

推荐练习：P1451 求细胞数量

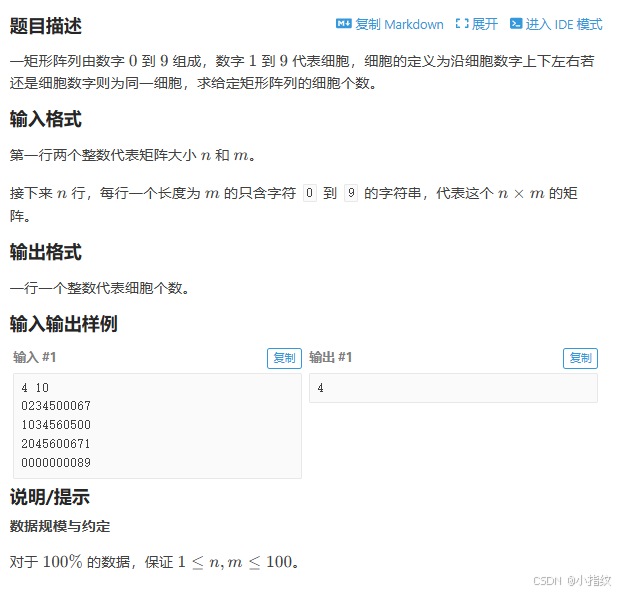
在这里插入图片描述

很相似的一道，直接上代码吧~

#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define int long long
#define PII pair<int,int>
#define fi first
#define se second
#define endl '\n'
const int N=105;
int n,m;
char a[N][N]; 
int dx[]={1,0,-1,0};
int dy[]={0,1,0,-1};
void dfs(int x,int y)
{if(x<=0||x>n||y<=0||y>m||a[x][y]=='0') return ;a[x][y]='0';for(int i=0;i<4;i++){int tx=x+dx[i];int ty=y+dy[i];dfs(tx,ty);}
}
void solve()
{int ans=0;cin>>n>>m;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++)cin>>a[i][j];}for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){if(a[i][j]!='0'){ans++;dfs(i,j);}}}cout<<ans;
}
signed main()
{IOS;int _=1;
//	cin>>_;while(_--)solve();return 0;
}

棋盘问题

1114. 棋盘问题

1114. 棋盘问题
在这里插入图片描述

题目的要求还是嗯明确的，

保证每行每列最多只放一个棋子
#区域才能放棋子，不能把棋子房子 . 即空白区域。

可以先看这个问题：
在这里插入图片描述
以3*3为例，只有以下这六种方案，我们可以通过枚举每一行放在第即列，如果第一行放在了第一列，那么后面枚举的时候第一列就不能在放了。

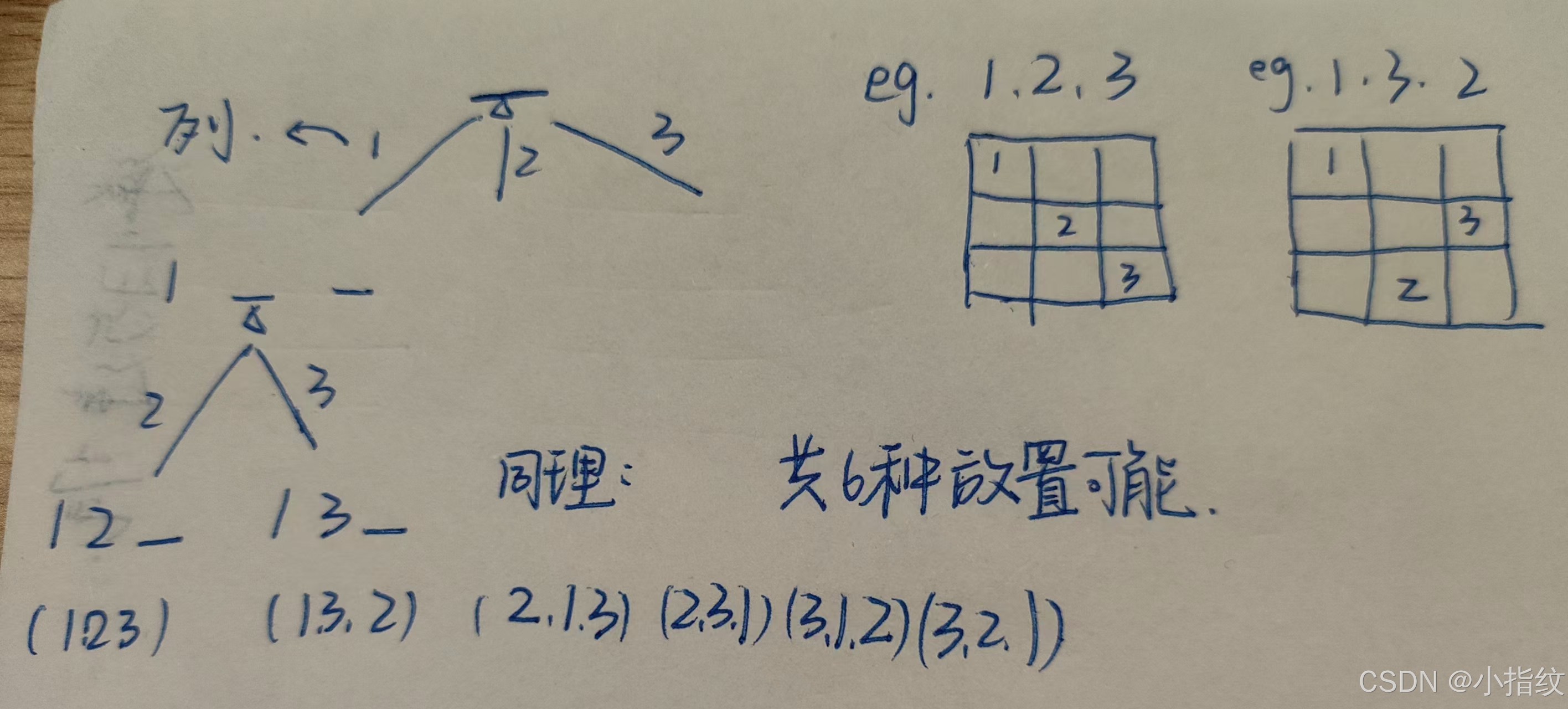
以此为例那么这道题我们只需多判断一下它再这个位置时能否放棋子，以及放k个棋子有多少种情况。

#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define int long long
#define PII pair<int,int>
#define fi first
#define se second
#define endl '\n'
const int N=10;
int n,k;
char g[N][N];
int ans=0;//记录方案数 
int st[N];//记录某一列有没有被占 
void dfs(int x,int cnt)//x表示当前枚举到第几行，cnt是记录当前棋子用了多少
{if(cnt==k)//当 {ans++;return ;}if(x>= n) return ;for(int i=0;i<n;i++){if(!st[i]&&g[x][i]=='#')//如果当前列没被占，并且当前位置可以放棋子{st[i]=1;dfs(x+1,cnt+1);st[i]=0;} }dfs(x+1,cnt);//访问下一行	
} 
void solve()
{while(cin>>n>>k){if(n==-1&&k==-1)return;for(int i=0;i<n;i++)cin>>g[i];ans=0;dfs(0,0);cout<<ans<<endl;}
}
signed main()
{IOS;int _=1;
//	cin>>_;while(_--)solve();return 0;
}

推荐练习：P1219 [USACO1.5] 八皇后 Checker Challenge

数的划分

P1025 数的划分

P1025 [NOIP 2001 提高组] 数的划分

在这里插入图片描述

因为这道题三个数不同的顺序也只算一种，所以我们可以用排列数来做，只枚举按字典序排列小的那一种情况，然后记录符合情况的就可以啦。注意剪枝，不然会T

#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define int long long
#define PII pair<int,int>
#define fi first
#define se second
#define endl '\n'
const int N=206;
int n,k,ans,a[N];
void dfs(int x,int st,int sum)
//分别代表当前枚举到的位置，当前第一个能枚举的数，以及当前数的总和 
{if(sum>n)return ;if(x>k){if(sum==n)ans++;return;}for(int i=st;sum+i*(k-x+1)<=n;i++){a[x]=i;dfs(x+1,i,sum+i);a[x]=0;}
}
void solve()
{cin>>n>>k;dfs(1,1,0);cout<<ans;
}
signed main()
{IOS;int _=1;
//	cin>>_;while(_--)solve();return 0;
}