Unity-NavMesh详解-其二

终于来写我们一直拖着的NavMesh的内容了：

我们先来看这么一个界面：这是我们的recast navigation给的一个具体的Recast Demo，我们可以根据cmake文件来具体构建一个可执行文件实现可视化。

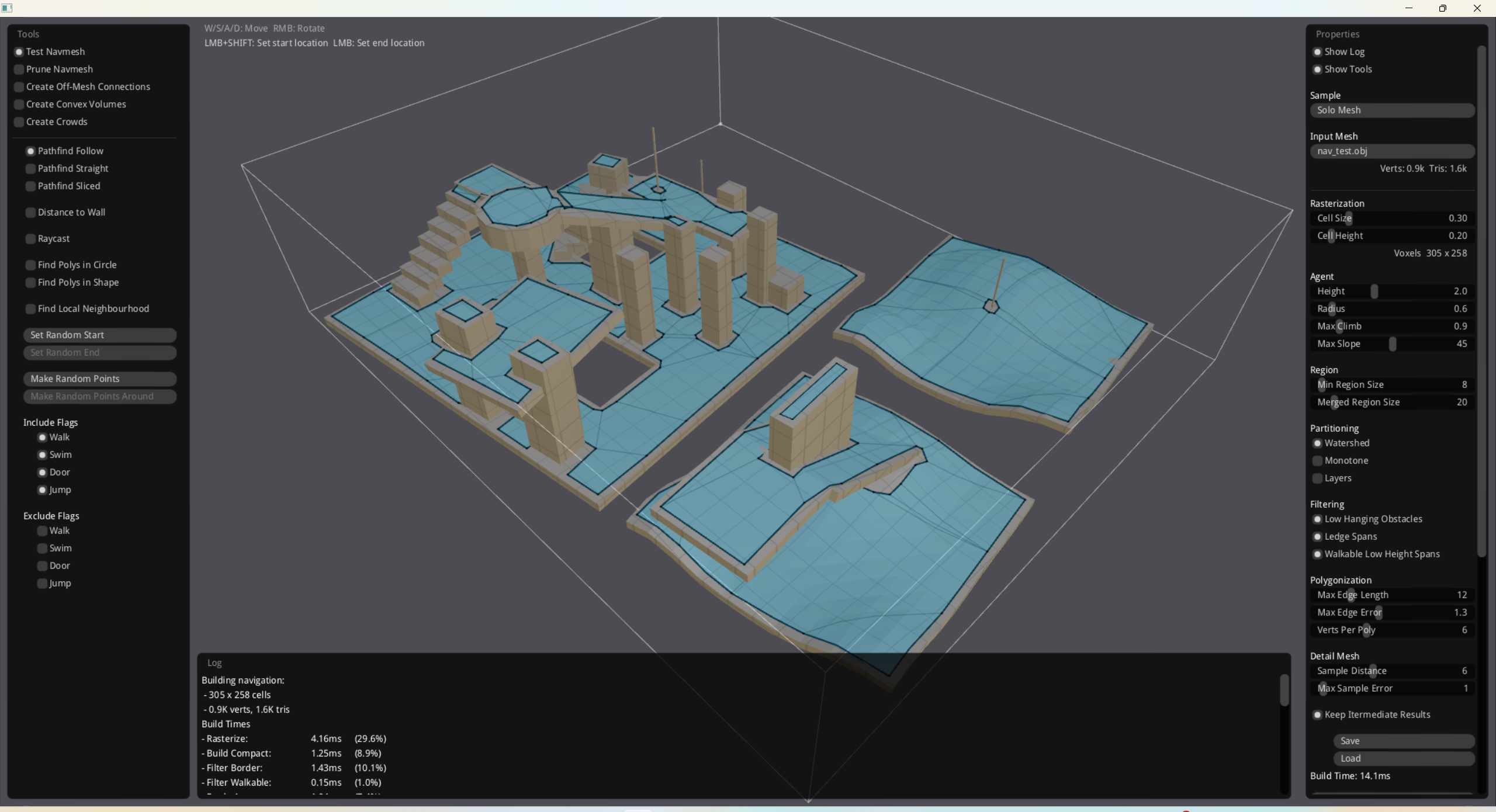
可以看到有很多参数啊，我们一个一个地来说：

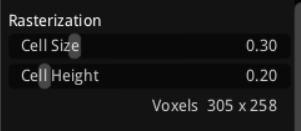
Rasterization面板控制navmesh生成的第一步，即将3D几何模型转换为体素（voxel）网格的过程，其中Cell Size（单元格大小，默认0.3）定义水平方向每个voxel的尺寸，影响整体分辨率，越小越精确但计算更慢，一般值设置为Agent半径的0.5倍以捕捉细微通道；Cell Height（单元格高度，默认0.2）定义垂直方向voxel的高度，决定了高度差的检测精度，与最大攀爬高度相关联，建议值与Cell Size协调以处理台阶或坡度；Voxels（体素计数，如305 x 258）是自动计算的网格尺寸，代表模型在该分辨率下的体素数量，直接影响内存和构建时间，如果模型大可增大Cell Size以减少voxel总数，从而加速大规模场景的处理。

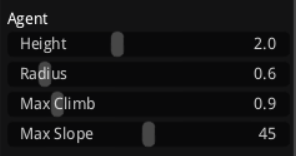
Agent面板定义行走代理的物理属性，用于过滤可行走区域，其中Height（代理高度，默认2.0）表示代理的垂直尺寸，确保navmesh排除太低的通道，建议值为角色实际高度如人类1.8-2.0以适应低矮环境；Radius（代理半径，默认0.6）代表代理的水平宽度，创建边缘缓冲区防止卡住，建议值0.5-1.0根据角色大小调整以优化窄道通行；Max Climb（最大攀爬高度，默认0.9）指定代理能越过的台阶高度，促进navmesh连接分层表面，一般值为台阶的1.5倍以处理楼梯或平台；Max Slope（最大坡度，默认45度）设定可行走的坡度阈值，超过则视为墙壁，这些参数共同影响navmesh的可达性，修改后需重新构建以更新网格。

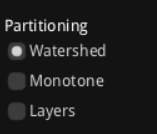
Partitioning面板选择区域分割算法，用于将体素分组为连通区域，其中Watershed（分水岭算法，已选中）是一种默认方法，通过模拟水流分割区域，提供平衡的精度和性能，适合复杂地形以生成自然连通的navmesh；Monotone（单调算法）使用水平扫描线简化分割，更快但可能在垂直结构中丢失细节，建议用于简单平面场景；Layers（层级算法）按高度层分割，优化多层建筑如楼层，建议在有叠加结构的模型中使用，这些选项影响区域的生成效率和质量，选择后会改变navmesh的连通性和构建速度，Watershed通常是最通用的起点。

这里补充一下分水岭算法的概念：分水岭算法（Watershed Algorithm）是一种经典的图像分割方法，源自地理学中的“分水岭”概念，指山脊线将雨水分流到不同盆地的界线；在Recast Navigation中，它被应用于Partitioning（区域分割）阶段，将栅格化后的体素（voxel）网格分割成独立的连通区域，具体过程模拟从高处（体素高度）向低处“注水”，水流会自然形成“盆地”（regions），盆地间的“分水岭”则成为区域边界，这种方法特别适合复杂地形，能生成自然的、可连通的区域分割，提供较高的精度和鲁棒性，但计算量稍大，相比Monotone算法更慢却更准确，建议在有不规则坡度或多层结构的模型中使用，以优化navmesh的连通性和路径质量。

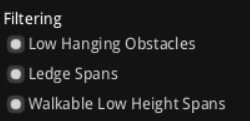
Filtering面板启用体素过滤选项，以移除不可行走特征，其中Low Hanging Obstacles（低悬挂障碍，已选中）过滤代理头部下方的低矮障碍如枝条，确保代理不会卡在低处，建议在有天花板或悬挂物的场景启用以提高安全性；Ledge Spans（边缘跨度，已选中）标记和过滤悬崖或边缘跨度，防止代理从高处掉落，建议用于有平台或悬崖的地图以增强路径可靠性；Walkable Low Height Spans（可行走低高度跨度，已选中）过滤太低的跨度区域如狭窄缝隙，基于代理高度排除不可达部分，建议在洞穴或低矮环境中启用，这些过滤共同精炼体素数据，减少噪声并优化navmesh的可行走性，启用过多可能增加构建时间但提升精度。

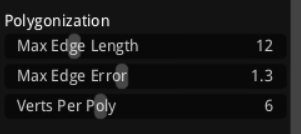
Polygonization面板控制将区域转换为导航多边形的简化过程，其中Max Edge Length（最大边缘长度，默认12）限制多边形边缘的最大长度，超过则分割以提高路径精度，建议值10-20用于大开放区域以避免长直线偏差；Max Edge Error（最大边缘误差，默认1.3）定义简化边缘时的允许偏差，平衡形状准确性和顶点减少，建议值1.0-1.5以优化性能而不丢失细节；Verts Per Poly（每个多边形的最大顶点，默认6）限制多边形的复杂度，防止过于复杂的形状影响查询效率，建议值3-6以保持简单，这些参数影响navmesh的多边形质量和大小，调整后可减少内存占用并加速寻路。

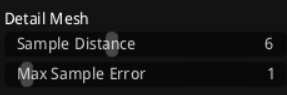
Detail Mesh面板优化navmesh的细节三角网格，用于更精确的路径采样，其中Sample Distance（采样距离，默认6）控制三角网格的采样间距，值越小细节越丰富但内存增加，建议值4-8用于中等精度以平衡路径平滑和性能；Max Sample Error（最大采样误差，默认1）限制采样时的高度偏差，确保三角网格贴合原始几何，建议值1-2以避免路径不准，这些参数在navmesh生成后期添加细节，支持更平滑的移动和查询，禁用（设0）可简化但降低准确性。

这里还提供了一些NavMesh的相关工具：其中Test Navmesh（测试navmesh，已选中）允许在生成的navmesh上进行路径查找和查询，如设置起点终点测试A路径；Prune Navmesh（修剪navmesh）移除不必要的多边形以优化大小；Create Off-Mesh Connections（创建离线连接）手动添加跳跃或桥接链接，连接不连通区域；Create Convex Volumes（创建凸体体积）绘制凸形标记区域如不可走区或特殊地带；Create Crowds（创建群体）模拟多个代理的移动和避障，这些工具扩展navmesh功能，适合在生成后细化或验证，Test Navmesh是入门测试寻路的起点。

关于具体的导航网格生成过程，我们在第一篇笔记中已经写得非常详细了，所以我们就按下不表，接下来我们来把目光放在具体的寻路算法和避障算法上。

寻路

dtStatus dtNavMeshQuery::findPath(dtPolyRef startRef, dtPolyRef endRef,const float* startPos, const float* endPos,const dtQueryFilter* filter,dtPolyRef* path, int* pathCount, const int maxPath) const
{// ...参数校验和初始化...m_nodePool->clear();m_openList->clear();// 起点入open listdtNode* startNode = m_nodePool->getNode(startRef);dtVcopy(startNode->pos, startPos);startNode->pidx = 0;startNode->cost = 0;startNode->total = dtVdist(startPos, endPos) * H_SCALE;startNode->id = startRef;startNode->flags = DT_NODE_OPEN;m_openList->push(startNode);dtNode* lastBestNode = startNode;float lastBestNodeCost = startNode->total;while (!m_openList->empty()){// 取出open list中总代价最小的节点dtNode* bestNode = m_openList->pop();bestNode->flags &= ~DT_NODE_OPEN;bestNode->flags |= DT_NODE_CLOSED;// 到达终点if (bestNode->id == endRef){lastBestNode = bestNode;break;}// 遍历所有相邻多边形for (unsigned int i = bestPoly->firstLink; i != DT_NULL_LINK; i = bestTile->links[i].next){dtPolyRef neighbourRef = bestTile->links[i].ref;// 跳过无效或回头的多边形if (!neighbourRef || neighbourRef == parentRef)continue;// 过滤不可通行区域if (!filter->passFilter(neighbourRef, neighbourTile, neighbourPoly))continue;// 获取或创建邻居节点dtNode* neighbourNode = m_nodePool->getNode(neighbourRef, crossSide);if (!neighbourNode)continue;// 计算代价和启发式float cost = bestNode->cost + filter->getCost(...);float heuristic = dtVdist(neighbourNode->pos, endPos) * H_SCALE;float total = cost + heuristic;// 如果已有更优路径，跳过if ((neighbourNode->flags & DT_NODE_OPEN) && total >= neighbourNode->total)continue;if ((neighbourNode->flags & DT_NODE_CLOSED) && total >= neighbourNode->total)continue;// 更新节点信息并加入open listneighbourNode->pidx = m_nodePool->getNodeIdx(bestNode);neighbourNode->id = neighbourRef;neighbourNode->flags = (neighbourNode->flags & ~DT_NODE_CLOSED);neighbourNode->cost = cost;neighbourNode->total = total;if (neighbourNode->flags & DT_NODE_OPEN)m_openList->modify(neighbourNode);else{neighbourNode->flags = DT_NODE_OPEN;m_openList->push(neighbourNode);}// 记录到终点的最近节点if (heuristic < lastBestNodeCost){lastBestNodeCost = heuristic;lastBestNode = neighbourNode;}}}// ...回溯路径，输出结果...
}

NavMesh中具体的寻路算法的底层实现就是我们常说的A-star算法。

它首先对输入参数进行校验和初始化，然后清空节点池和open list（优先队列），将起点节点加入open list，并初始化总代价（cost+heuristic）。在主循环中，每次从open list中取出总代价最小的节点（即当前最有希望到达终点的节点），如果该节点就是终点，则寻路结束；否则遍历所有与当前节点相邻的多边形（即可达的下一个区域），对每个邻居节点，先进行有效性和可通行性检查，再计算从起点到该邻居的实际代价（cost）和到终点的启发式距离（heuristic），两者相加得到总代价。如果该邻居节点已经有更优的路径，则跳过，否则更新其父节点、总代价等信息，并将其加入open list。整个过程中，算法会不断记录距离终点最近的节点，以便在找不到完全路径时返回最优近似路径。最终，算法通过回溯父节点链表，输出一条从起点到终点的最优路径。

作为NavMesh中核心的寻路算法，优化思路有很多，接下来我通过伪代码列举一些可能的优化方法。

分层寻路：

// 1. 构建高层图（每个Tile/区域为一个节点，边为可达关系）
struct TileNode { int id; std::vector<int> neighbors; };// 2. 高层A*：在TileNode之间寻路，得到Tile序列
std::vector<int> highLevelPath = AStar(tileGraph, startTile, endTile);// 3. 低层A*：在每个Tile内部用Detour原生A*细化路径
for (int i = 0; i < highLevelPath.size() - 1; ++i) {// 在Tile[i]内部用findPath()，起点为上一个Tile的出口，终点为下一个Tile的入口std::vector<PolyRef> subPath = detour.findPath(...);// 合并到总路径
}

如果我们是一个大地图，具体的节点很多，那么我们可以在Tile Mesh模式下，先用Tile为单位做高层寻路，再用Detour的findPath做细化。

分层寻路中的“Tile”就是我们在地图区域划分时的Tile单元，也就是Recast/Detour在大地图NavMesh构建时的瓦片区块。当地图较大时，我们可以先以这些区域（Tile）为单位进行一次高层次的寻路，快速确定经过哪些区块，然后再在每个具体的区域内部用更精细的寻路算法（如A）计算实际的行走路径。这样分两层进行寻路，能够显著减少全局A的扩展节点数量，提升大规模场景下的寻路效率和响应速度，是大型游戏和仿真系统中常用的寻路加速方案。

双向A：

// 初始化两个open list
OpenList openStart, openEnd;
openStart.push(startNode);
openEnd.push(endNode);while (!openStart.empty() && !openEnd.empty()) {// 从起点方向扩展Node* nodeFwd = openStart.pop();// ...常规A*扩展...if (nodeFwd在openEnd已访问) {// 两边相遇，拼接路径return 合并路径(nodeFwd, openEnd中对应节点);}// 从终点方向扩展Node* nodeBwd = openEnd.pop();// ...常规A*扩展...if (nodeBwd在openStart已访问) {return 合并路径(openStart中对应节点, nodeBwd);}
}

双向A（Bidirectional A）的核心思想就是：在已知起点和终点的情况下，同时从起点和终点各自出发，各自执行A寻路算法，分别维护两个开放队列（open list）。每次轮流从两个方向扩展节点，当发现两个队列中有节点重合（即某个节点被两边都访问到）时，就说明已经找到了一条从起点到终点的可行路径。此时可以通过回溯两边的父节点，将路径拼接起来，得到完整的最优路径。

这种方法通常能显著减少搜索空间，提升长距离寻路的效率，尤其适合大地图或起终点距离较远的场景。

OpenList优化：

// 假设总代价范围有限，可用数组桶
std::vector<std::vector<Node*>> buckets;
int minCost = ...;
int maxCost = ...;
for (int cost = minCost; cost <= maxCost; ++cost) {for (Node* node : buckets[cost]) {// 处理该总代价的所有节点}
}

一般的开放队列使用二叉堆实现，特定情况下可以用更高效的数据结构（如斐波那契堆、桶队列）减少插入/弹出耗时。

斐波那契堆是一种由多棵最小堆有序的多叉树组成的数据结构，所有树的根节点通过循环链表连接，插入新节点和减少关键字操作都可以在O(1)的摊还时间内完成，而取出最小值的操作是O(log n)。在A寻路算法中，open list需要频繁插入新节点、取出总代价最小的节点以及动态更新节点的优先级（decrease-key），斐波那契堆非常适合这种大规模、频繁优先级更新的场景。具体用法是：每当A扩展到新多边形时，将其作为新节点插入斐波那契堆；每次主循环时，从堆中取出总代价最小的节点进行扩展；如果发现某个节点有更优路径到达，则用decrease-key操作更新其优先级。这样可以显著提升大地图、复杂环境下A寻路的整体效率。不过，如果节点数量不大或优先级更新不频繁，二叉堆实现更简单、常数更小，实际效果可能更好。

桶队列（Bucket Queue）的核心思想，就是根据节点的优先级（在A中通常是总代价函数的值）将所有节点分配到不同的“桶”中。这里的“桶”可以是链表，也可以是数组，而整个桶队列就是由多个这样的桶（链表或数组）组成的一个数组或列表。每当我们插入一个新节点时，就根据它的优先级（总代价）直接放入对应优先级的桶中；如果该优先级还没有桶，就新建一个桶（链表/数组）来存放。查找最小优先级节点时，只需要从优先级最小的非空桶中取出一个节点即可，这样理论上所有操作（插入、取最小、减少关键字）都可以达到O(1)的效率，前提是优先级范围有限且分布较为集中。

在导航网格寻路中，A算法的open list就可以用桶队列来实现：每个节点的总代价（优先级）由代价函数计算得出，总代价相同的节点放在同一个桶里。每次扩展节点时，直接从总代价最小的桶中取出节点即可，这样可以极大提升效率。但如果总代价的取值范围很大或者分布很稀疏，桶的数量就会变多，空间浪费严重，查找最小优先级桶的效率也会下降，极端情况下会退化到和普通优先队列（如二叉堆）一样的复杂度。因此，桶队列最适合优先级范围有限、分布集中的场景，在这种情况下可以实现所有操作的O(1)效率。

避障

在Recast Navigation项目中，动态避障主要由DetourCrowd模块负责实现。它的核心思想是：在全局路径规划（A算法）生成的导航路径基础上，每个智能体（Agent）在移动过程中会实时感知周围的其他Agent和动态障碍物，根据当前速度、目标点和邻居的位置，动态调整自己的速度和移动方向，从而有效避免与其他移动体发生碰撞。这一过程通常采用局部避障算法（如RVO、ORCA等原理），通过预测未来的运动趋势，提前规避潜在冲突。此外，DetourCrowd还支持群体行为模拟和局部路径重规划，使得多个Agent能够在复杂、动态变化的环境中高效、自然地协同移动，实现了真实感很强的动态避障效果。

我们先来看看一些简单的局部避障算法，我用伪代码来表明其含义：

VO（Velocity Obstacle，速度障碍）

for (int i = 0; i < obstacle_count; ++i) {Vector2 rel_pos = obstacle[i].pos - agent.pos;Vector2 rel_vel = agent.vel - obstacle[i].vel;DangerZone dz = compute_velocity_obstacle(rel_pos, obstacle[i].radius, time_window);add_to_all_danger_zones(dz);
}// 在所有危险区间外选择一个速度
for (int j = 0; j < candidate_vel_count; ++j) {if (!in_any_danger_zone(candidate_vel[j], all_danger_zones)) {agent.vel = candidate_vel[j];break;}
}

VO算法通过计算每个障碍物与自身的相对速度和位置，推导出一组“危险速度区间”，只要Agent选择的速度不落在这些区间内，就能避免未来发生碰撞。它只考虑自身主动避让，适合单Agent场景。

RVO（Reciprocal Velocity Obstacle，对等速度障碍）

for (int i = 0; i < neighbor_count; ++i) {Vector2 rel_pos = neighbor[i].pos - agent.pos;Vector2 rel_vel = agent.vel - neighbor[i].vel;DangerZone rvo_zone = compute_rvo(rel_pos, rel_vel, agent.radius, neighbor[i].radius, time_window);add_to_all_rvo_zones(rvo_zone);
}// 选择一个不在任何RVO区间内的速度
for (int j = 0; j < candidate_vel_count; ++j) {if (!in_any_rvo_zone(candidate_vel[j], all_rvo_zones)) {agent.vel = candidate_vel[j];break;}
}

RVO算法假设所有Agent都在主动避让，计算时将速度调整分摊给双方。每个Agent选择一个不在RVO危险区间内的速度，从而实现更自然的多Agent避障，避免“你让我也让”的僵局。

在源码中，具体使用了哪种动态避障算法呢？

int dtObstacleAvoidanceQuery::sampleVelocityAdaptive(const float* pos, const float rad, const float vmax,const float* vel, const float* dvel, float* nvel,const dtObstacleAvoidanceParams* params,dtObstacleAvoidanceDebugData* debug)
{prepare(pos, dvel); // 预处理障碍物信息memcpy(&m_params, params, sizeof(dtObstacleAvoidanceParams));m_invHorizTime = 1.0f / m_params.horizTime;m_vmax = vmax;m_invVmax = vmax > 0 ? 1.0f / vmax : FLT_MAX;dtVset(nvel, 0,0,0);if (debug)debug->reset();// 构建采样模式（围绕期望速度的多个方向和半径）float pat[(DT_MAX_PATTERN_DIVS*DT_MAX_PATTERN_RINGS+1)*2];int npat = 0;// ... 省略采样点生成代码 ...// 多层采样，逐步细化float cr = vmax * (1.0f - m_params.velBias);float res[3];dtVset(res, dvel[0] * m_params.velBias, 0, dvel[2] * m_params.velBias);int ns = 0;for (int k = 0; k < depth; ++k){float minPenalty = FLT_MAX;float bvel[3];dtVset(bvel, 0,0,0);for (int i = 0; i < npat; ++i){float vcand[3];vcand[0] = res[0] + pat[i*2+0]*cr;vcand[1] = 0;vcand[2] = res[2] + pat[i*2+1]*cr;if (dtSqr(vcand[0])+dtSqr(vcand[2]) > dtSqr(vmax+0.001f)) continue;const float penalty = processSample(vcand,cr/10, pos,rad,vel,dvel, minPenalty, debug);ns++;if (penalty < minPenalty){minPenalty = penalty;dtVcopy(bvel, vcand);}}dtVcopy(res, bvel);cr *= 0.5f; // 逐步缩小采样半径}dtVcopy(nvel, res);return ns;
}

每一帧，系统会在速度空间内围绕Agent的期望速度采样大量候选速度（不同方向和速度大小），对每个候选速度，调用processSample函数综合评估其与障碍物发生碰撞的风险、与期望速度的偏离程度等，计算一个“惩罚值”（penalty）。最终，Agent选择惩罚值最小的速度作为自己的新速度，从而既能尽量接近期望目标，又能有效避开周围的动态和静态障碍。

processSample函数的具体实现如下：

float dtObstacleAvoidanceQuery::processSample(const float* vcand, const float cs,const float* pos, const float rad,const float* vel, const float* dvel,const float minPenalty,dtObstacleAvoidanceDebugData* debug)
{// 1. 惩罚项：与期望速度和当前速度的偏离const float vpen  = m_params.weightDesVel * (dtVdist2D(vcand, dvel) * m_invVmax);const float vcpen = m_params.weightCurVel * (dtVdist2D(vcand, vel) * m_invVmax);// 2. 计算与障碍物的碰撞时间阈值float minPen = minPenalty - vpen - vcpen;float tThresold = (m_params.weightToi / minPen - 0.1f) * m_params.horizTime;if (tThresold - m_params.horizTime > -FLT_EPSILON)return minPenalty; // 惩罚过大，提前返回// 3. 计算与所有圆形障碍物的最小碰撞时间float tmin = m_params.horizTime;float side = 0;int nside = 0;for (int i = 0; i < m_ncircles; ++i){const dtObstacleCircle* cir = &m_circles[i];// RVO思想：计算相对速度float vab[3];dtVscale(vab, vcand, 2);dtVsub(vab, vab, vel);dtVsub(vab, vab, cir->vel);// 侧向惩罚side += dtClamp(dtMin(dtVdot2D(cir->dp,vab)*0.5f+0.5f, dtVdot2D(cir->np,vab)*2), 0.0f, 1.0f);nside++;float htmin = 0, htmax = 0;if (!sweepCircleCircle(pos,rad, vab, cir->p,cir->rad, htmin, htmax))continue;// 处理重叠if (htmin < 0.0f && htmax > 0.0f)htmin = -htmin * 0.5f;if (htmin >= 0.0f && htmin < tmin){tmin = htmin;if (tmin < tThresold)return minPenalty;}}// 4. 计算与所有线段障碍物的最小碰撞时间for (int i = 0; i < m_nsegments; ++i){const dtObstacleSegment* seg = &m_segments[i];float htmin = 0;if (seg->touch){// 靠得很近，立即碰撞float sdir[3], snorm[3];dtVsub(sdir, seg->q, seg->p);snorm[0] = -sdir[2];snorm[2] = sdir[0];if (dtVdot2D(snorm, vcand) < 0.0f)continue;htmin = 0.0f;}else{if (!isectRaySeg(pos, vcand, seg->p, seg->q, htmin))continue;}htmin *= 2.0f;if (htmin < tmin){tmin = htmin;if (tmin < tThresold)return minPenalty;}}// 5. 归一化侧向惩罚if (nside)side /= nside;// 6. 计算最终惩罚分数const float spen = m_params.weightSide * side;const float tpen = m_params.weightToi * (1.0f/(0.1f+tmin*m_invHorizTime));const float penalty = vpen + vcpen + spen + tpen;// 7. 记录调试信息if (debug)debug->addSample(vcand, cs, penalty, vpen, vcpen, spen, tpen);return penalty;
}

对于每一个候选速度，系统会综合评估它与期望速度和当前速度的偏离程度、与周围障碍物（包括其他Agent和静态障碍）的最小碰撞时间，以及侧向避让的安全性等因素，分别计算出对应的惩罚分数，然后将这些分数加权相加得到一个总的惩罚值。最终，所有候选速度中惩罚值最低的那个被选为Agent的下一步移动速度，这样既能保证Agent尽量朝目标方向平滑移动，又能有效避开动态和静态障碍，实现了高效、智能的动态避障行为。

通俗的说就是：

1. 这种速度是不是朝着目标方向走的（越接近目标方向分数越低）；
2. 这种速度会不会很快撞上别人或障碍物（越安全分数越低）；
3. 这种速度是不是和自己当前的速度差别太大（越平滑分数越低）。

那现在理解了底层的动态避障算法后，我们如何去优化呢？

ORCA（Optimal Reciprocal Collision Avoidance，最优对等碰撞规避）

for (int i = 0; i < neighbor_count; ++i) {Line orca_line = compute_orca_line(agent, neighbor[i], time_window);add_to_all_orca_lines(orca_line);
}// 在所有ORCA半平面内，选择距离期望速度最近的速度
Vector2 best_vel = agent.pref_vel;
for (int k = 0; k < orca_line_count; ++k) {if (!in_orca_halfplane(best_vel, orca_lines[k])) {best_vel = project_to_orca_halfplane(best_vel, orca_lines[k]);}
}
agent.vel = best_vel;

ORCA（Optimal Reciprocal Collision Avoidance）算法是一种用于多智能体系统的高效动态避障算法，其核心思想是在每一帧，每个Agent都会在速度空间中进行采样，并根据自己与其他Agent之间的距离和速度关系进行判断。与传统的VO（速度障碍）算法不同，VO算法假设碰撞规避的责任完全由自己承担，因此当检测到与其他Agent有碰撞风险时，自己必须大幅调整速度，而对方Agent则不做任何让步，这在多Agent场景下容易导致所有Agent都过度减速，效率低下。而ORCA算法的核心假设是，任何两个Agent都各自承担一半的避让责任，也就是说，当A和B有碰撞风险时，双方都只需各自调整一半的速度，具体做法是先计算出各自需要调整的速度，然后取两者的中点作为新的分界线，双方都将自己的速度调整到这条分界线的安全一侧。这样，每个Agent在每一帧都要与所有可能发生碰撞的其他Agent和障碍物分别进行速度空间的分界线划分，最终将所有安全速度区域的交集作为自己的可选速度区间，并在其中选择最接近当前期望速度的那个速度作为本帧的实际移动速度。通过这种方式，ORCA算法既能保证所有Agent安全避障，又能避免过度减速，实现高效、自然的多智能体动态避障。

值得一题的是在A-star算法计算出的静态路径规划的基础上，我们其实往往不仅仅是一个避障就解决的问题，当我们在运行时发现了障碍或者其他agent，往往要牵扯到一系列内容：

当Agent在实际运行过程中遇到障碍物或其他Agent时，系统首先会通过局部避障算法（如DetourCrowd的速度采样与打分机制）尝试在当前路径上调整自身的速度和方向，以实现即时的避让和安全通行。如果局部避障能够解决问题，Agent会继续沿着原有的全局路径前进，只是移动轨迹会临时发生偏移；但如果局部避障无法有效绕开障碍（比如前方完全被堵死、动态障碍长时间阻挡、或偏离原路径过远），系统就需要触发局部路径重规划或全局路径重规划。这时，Agent会以当前位置为新的起点，重新在NavMesh上用A等算法计算一条到目标的新路径，并用Funnel等算法进行路径平滑，确保转向自然。

所以我们除了想办法优化局部避障算法以外，还要考虑一个问题就是我们的路径平滑算法。

Funnel算法：

Funnel算法（通道算法）是路径平滑的基础层，它能将A或NavMesh多边形路径转化为一条最短、无碰撞的折线，为后续的曲线平滑（如贝塞尔插值）提供基础。

// 输入：portals为多边形路径的边界点对（每一对为一个门），start为起点
// 输出：result为平滑后的折线路径
void funnelAlgorithm(Vector2* portals_left, Vector2* portals_right, int num_portals, Vector2 start, Vector2* result, int* result_count)
{int apexIndex = 0, leftIndex = 0, rightIndex = 0;Vector2 apex = start;Vector2 left = portals_left[0];Vector2 right = portals_right[0];result[0] = apex;*result_count = 1;for (int i = 1; i < num_portals; ++i) {Vector2 newLeft = portals_left[i];Vector2 newRight = portals_right[i];// 更新右边界if (triangleArea2D(apex, right, newRight) <= 0.0f) {if (apex == right || triangleArea2D(apex, left, newRight) > 0.0f) {right = newRight;rightIndex = i;} else {// 走到左边界，apex前进apex = left;apexIndex = leftIndex;result[(*result_count)++] = apex;left = apex;right = apex;leftIndex = apexIndex;rightIndex = apexIndex;i = apexIndex;continue;}}// 更新左边界if (triangleArea2D(apex, left, newLeft) >= 0.0f) {if (apex == left || triangleArea2D(apex, right, newLeft) < 0.0f) {left = newLeft;leftIndex = i;} else {// 走到右边界，apex前进apex = right;apexIndex = rightIndex;result[(*result_count)++] = apex;left = apex;right = apex;leftIndex = apexIndex;rightIndex = apexIndex;i = apexIndex;continue;}}}// 终点result[(*result_count)++] = portals_left[num_portals-1];
}

给定一条多边形路径（即A算法输出的多边形序列），我们把每两个相邻多边形的公共边（交界线）提取出来，得到一系列线段，每个线段有两个端点，分别称为左点和右点。算法从起点出发，维护当前路径的apex点（即当前路径的拐点），并动态维护可行走区域的最左点和最右点。遍历所有交界线时，判断新的左点是否收紧了可行走区域的左边界（这个判断通常用三角形面积符号（叉积）来实现），若是则更新左点；判断新的右点是否收紧了右边界，若是则更新右点。如果发现新的左点已经跨过了当前右点，说明可行走区域被夹到极限，此时将apex点更新为当前右点，并把这个点作为拐点加入路径，然后重置apex、左点和右点，继续处理后续交界线。反之亦然，如果新的右点跨过了当前左点，也做类似处理。最后将终点加入路径。这样处理后，最终得到的路径是由起点、若干个拐点和终点组成的折线，每一段都保证在NavMesh的可行走区域内，且路径最短、不会穿越障碍。

贝塞尔曲线： 

这样我们就输出了一条折线了，在这个基础上我们就可以去实现一个折线转曲线的过程：

// 二次贝塞尔曲线插值
// 输入：P0, P1, P2为三控制点，step为采样间隔（如0.05），output为输出平滑点数组
void bezierQuadratic(Vector2 P0, Vector2 P1, Vector2 P2, float step, Vector2* output, int* out_count)
{int count = 0;for (float t = 0.0f; t <= 1.0f; t += step) {float u = 1.0f - t;Vector2 B;B.x = u*u*P0.x + 2*u*t*P1.x + t*t*P2.x;B.y = u*u*P0.y + 2*u*t*P1.y + t*t*P2.y;output[count++] = B;}*out_count = count;
}// 用法示例：对Funnel输出的折线每3个点做一次插值
for (int i = 0; i < num_points - 2; i += 2) {bezierQuadratic(waypoints[i], waypoints[i+1], waypoints[i+2], 0.05f, smooth_path + smooth_count, &segment_count);smooth_count += segment_count;
}

通过一组控制点（如P0、P1、P2），用数学公式对它们进行加权插值，生成一系列平滑过渡的中间点。二次贝塞尔曲线的公式是B(t) = (1-t)^2*P0 + 2*(1-t)*t*P1 + t^2*P2，t从0到1变化时，B(t)会在三点之间画出一条平滑的曲线。

具体贝塞尔曲线的内容可以自行查阅，之前在图形学的笔记中也做过介绍，这里就不再赘述。

群体寻路

聊完了Detour的部分，我们当然也要聊一聊DetourCrowd的部分：毕竟在真正的应用场景中，可不会只有一个Agent。

DetourCrowd模块主要实现了在导航网格（NavMesh）基础上的多智能体（Agent）群体移动与动态避障功能，其核心能力包括：支持同时管理大量Agent，每个Agent都可以独立发起全局路径规划（如A寻路），并在路径跟随过程中维护一条“路径走廊”，实现平滑且鲁棒的路径跟随；在每一帧，DetourCrowd会为每个Agent实时感知周围的其他Agent和动态障碍物，通过基于速度采样和打分的局部避障算法，动态调整Agent的移动速度和方向，从而有效避免碰撞，实现自然的群体避让行为；此外，DetourCrowd还支持动态障碍的增删和局部NavMesh的增量重建，使Agent能够适应环境的实时变化，并通过异步路径请求队列提升大规模Agent寻路的效率。整体而言，DetourCrowd为复杂场景下的AI群体导航、动态避障和群体行为模拟提供了高效、可扩展的底层支持。

避障算法和路径平滑算法的创新我之前也已经说得差不多了，现在我还想提出一个似乎与路径走廊差不多的创新点：全局路径缓存。

路径走廊（Path Corridor）是每个Agent内部维护的一条从当前位置到目标点的多边形序列，它的主要作用是让Agent能够在动态环境下平滑、鲁棒地跟随路径，并在遇到小范围偏离或障碍时进行局部修正。只要路径没有完全失效，Agent就可以一直沿用这条走廊，无需频繁全局重算路径，从而提升了导航的实时性和稳定性。

全局路径缓存是一种面向整个系统的路径结果复用机制，用于存储和复用不同Agent之间常用的起点-终点路径。当多个Agent请求相同或相似的路径时，系统可以直接返回缓存中的路径结果，避免重复进行A寻路计算，显著提升大规模群体AI的整体寻路效率和系统吞吐量，特别适合热点区域和重复路径场景。

路径走廊是每个Agent独有的、动态变化的即时路径缓存，主要用于单Agent的平滑移动和局部修正；而全局路径缓存是所有Agent共享的、长期存储的路径复用机制，主要用于减少全局寻路的重复计算。两者没有重复，路径走廊提升单Agent的移动鲁棒性，全局路径缓存提升系统整体性能，两者互为补充。

// 全局路径缓存结构
Map<PathKey, PathResult> globalPathCache;// 路径请求流程
PathResult requestPath(Vector3 start, Vector3 end, Filter filter) {PathKey key = hash(start, end, filter);if (globalPathCache.contains(key)) {// 命中缓存，直接返回return globalPathCache[key];} else {// 未命中，调用A*寻路PathResult path = AStarFindPath(start, end, filter);// 存入缓存globalPathCache[key] = path;return path;}
}

这段伪代码展示了全局路径缓存的基本实现思路：系统维护一个以“起点-终点-过滤器”为key的全局路径缓存表，每当有Agent请求路径时，先查找缓存，若命中则直接返回缓存结果，若未命中则调用A算法计算新路径，并将结果存入缓存。这样可以大幅减少重复路径的实时寻路计算，提升大规模群体AI的整体效率和响应速度。