【数据结构与算法】数据结构初阶:详解二叉树(一)

🔥个人主页:艾莉丝努力练剑
❄专栏传送门:《C语言》、《数据结构与算法》、C语言刷题12天IO强训、LeetCode代码强化刷题
🍉学习方向:C/C++方向
⭐️人生格言:为天地立心,为生民立命,为往圣继绝学,为万世开太平

再次提醒:为什么我们要学那么多的数据结构?这是因为没有一种数据结构能够去应对所有场景。我们在不同的场景需要选择不同的数据结构,所以数据结构没有谁好谁坏之分,而评估数据结构的好坏要针对场景,如果在一种场景下我们需要频繁地对头部进行插入删除操作,那么这个时候我们用链表;但是如果对尾部进行插入删除操作比较频繁,那我们用顺序表比较好。
因此,不同的场景我们选择不同的数据结构。
前言:本篇文章,我们开始来看二叉树相关的知识点,在初阶的数据结构与算法阶段,我们把知识点分成三部分,复杂度作为第一部分,顺序表和链表、栈和队列、二叉树为第二部分,排序为第二部分,我们之前已经介绍完了第一部分:算法复杂度,本文我们将正式开始学习第二部分中的二叉树部分内容啦。
注意,二叉树的学习需要一定的基础,涉及到【函数栈帧的创建与销毁】,而且二叉树基本上是递归算法的暴力美学。
链接: 【深入详解】函数栈帧的创建与销毁:寄存器、压栈、出栈、调用、回收空间
正片开始之前,我们来了解一下我们即将要来介绍、学习的这个数据结构——二叉树。
二叉树的作用:
(1)快速查找
二叉树(尤其是二叉排序树)可以用于高效的数据查找,其查找的时间复杂度为 O(logn),最坏情况下为O(n)。这种特性使得二叉树特别适合需要频繁查找、插入和删除操作的场景。(2)动态数据管理
由于二叉树支持动态查询,并且可以通过调整树的结构来优化性能(例如 AVL 树、红黑树),它被广泛应用于需要动态管理数据的场景,如数据库索引和内存管理。(3)有序序列生成
中序遍历一棵二叉排序树可以得到一个关键字的有序序列,这使得二叉树成为一种有效的排序工具。构造二叉排序树的过程本质上就是对无序序列进行排序的过程。(4)树状结构表示
许多现实世界的问题可以用树状结构来建模,例如网站目录结构、文件系统等。虽然这些结构可能不是严格的二叉树,但通过适当的转换,它们可以使用二叉树的相关算法来处理。
应用场景:
(1)网页爬虫中的遍历
在互联网工程中,当需要下载某个网站的所有网页时,可以利用二叉树的遍历算法来模拟这一过程。这种算法能够确保所有页面都被访问到,并且按照一定的顺序进行处理。(2)二叉树的展开
在某些特定的应用中,比如将二叉树转换为链表形式,可以通过递归的方式实现。例如,在先序遍历的顺序下,左子树会被移到右指针位置,而左子树的最后一个节点会指向原来的右子树。(3)平衡二叉树的应用
平衡二叉树(如 AVL 树、红黑树)通过保持树的高度平衡来确保查找、插入和删除操作的时间复杂度始终为O(logn)。这类树结构广泛应用于需要高性能数据检索的场景,例如数据库索引和操作系统调度器。(4)表达式树
表达式树是一种特殊的二叉树,其中叶子节点表示操作数,内部节点表示运算符。这种结构可以用于解析和求值数学表达式,并且在编译器设计中具有重要应用。(5)哈夫曼编码
哈夫曼树是一种带权路径长度最短的二叉树,常用于数据压缩领域。通过构建哈夫曼树,可以生成最优前缀编码,从而减少存储空间或传输成本。(6)决策树
在机器学习和人工智能领域,二叉树可以用来表示决策过程。每个节点代表一个特征判断,每个分支代表一个可能的结果,最终的叶子节点则代表最终的决策结果。
二叉树这个部分学起来不会容易,但是会让你觉得很有收获,你慢慢会觉得学二叉树很爽!
目录
正文
一、树
(一)树的概念与结构
1、概念与结构
2、非树形结构
3、注意事项
(二)树的相关术语整理
(三)树的表示方法——孩子兄弟表示法:
(四)树的实际应用场景
二、二叉树
(一)二叉树的概念与结构
1、概念
2、结构
(二)一些特殊的二叉树
1、满二叉树
2、完全二叉树
3、二叉树存储结构
(1)顺序结构
(2)链表结构
结尾
正文
一、树
树是什么?数据结构中的树和自然界中的树有什么联系吗?有。


树的根在地下,故曰“向阳而生”;树形结构的根在上面——
(一)树的概念与结构
1、概念与结构
树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。
(1)有一个特殊的结点,称为根结点,根结点没有前驱结点(父结点/双亲结点)。
(2)除根结点外,其余结点被分成 M(M>0) 个互不相交的集合 T1、T2、……、Tm ,其中每一个集合Ti(1 <= i <= m) 又是一棵结构与树类似的子树。每棵子树的根结点有且只有一个前驱,可以有 0 个或多个后继。因此,树是递归定义的。
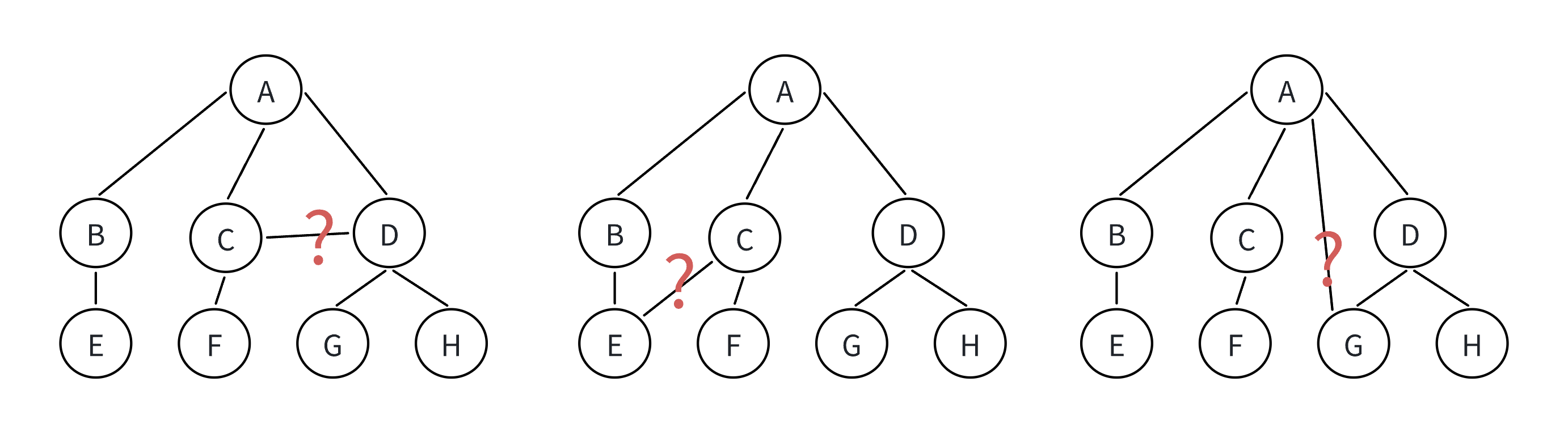
2、非树形结构
注意:树形结构中,子树之间不能有交集,否则就不是树形结构。
下面这些就不是树形结构,即非树形结构——
3、注意事项
(1)子树是不相交的(如果存在相交就是图了,图以后会介绍);
(2)除了根结点外,每个结点有且仅有一个父结点;
(3)一棵N个结点的树有N - 1条边 。
(二)树的相关术语整理
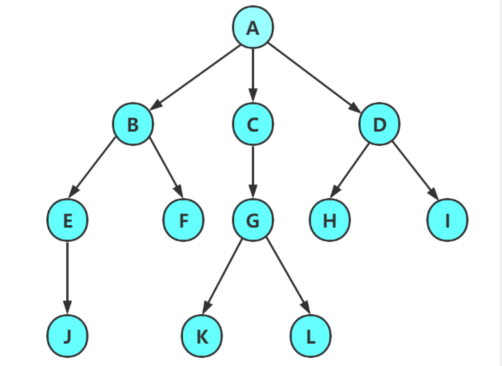
下图就是一个树形结构——
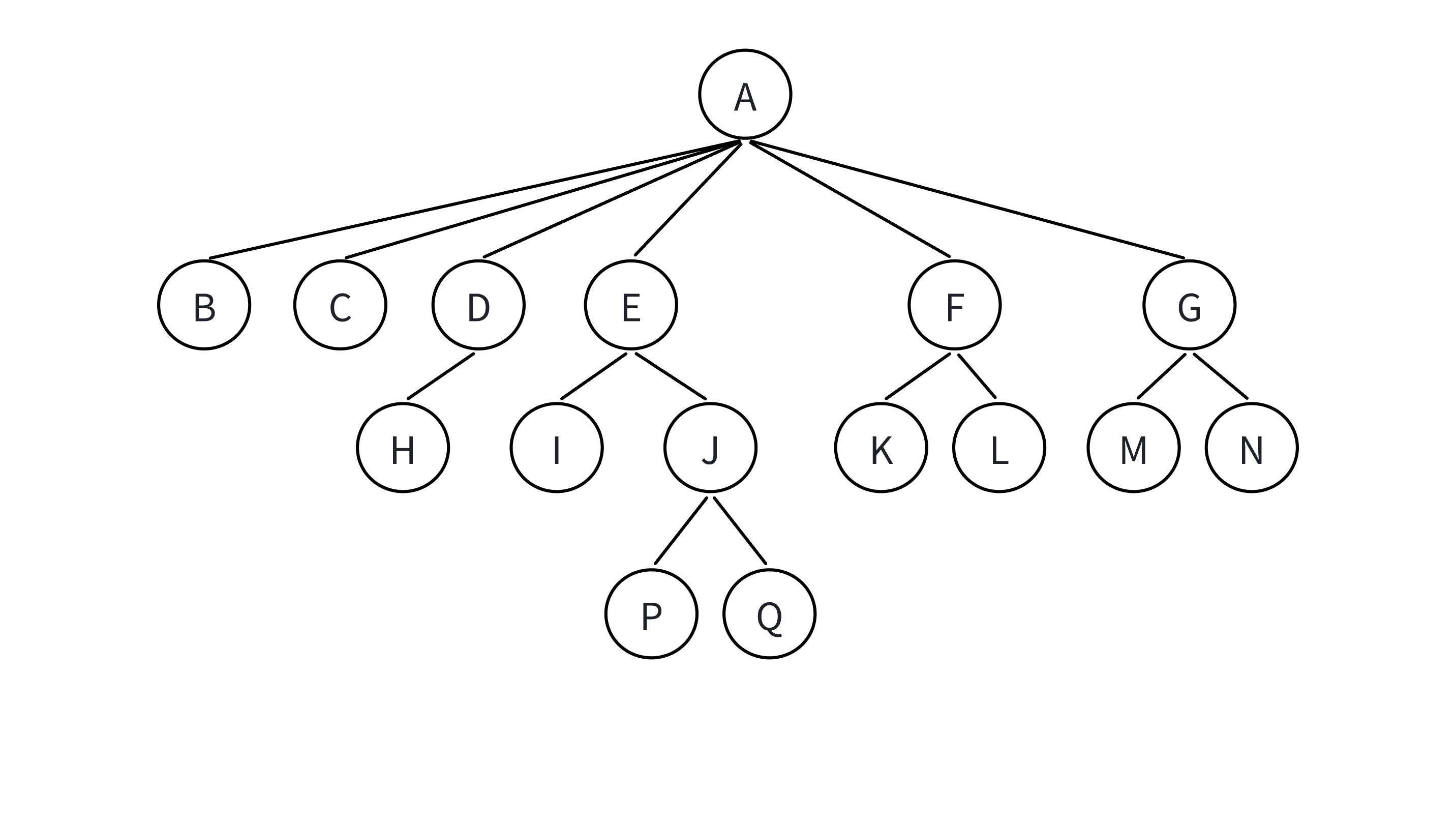
父结点/双亲结点:若一个结点含有子结点,则这个结点称为其子结点的父结点,如上图:A是B的父结点。
子结点/孩子结点:一个结点含有的子树的根结点称为该结点的子结点,如上图:B是A的孩子结点。
结点的度:一个结点有几个孩子,他的度就是多少,比如A的度为6,F的度为2,K的度为0。
树的度:一棵树中,最大的结点的度称为树的度,如上图:树的度为6。
叶子结点/终端结点:度为0的结点称为叶结点,如上图: B、C、H、I . . .等结点为叶结点。
分支结点/非终端结点:度不为0的结点,如上图: D、E、F、G... 等结点为分支结点。
兄弟结点:具有相同父结点的结点互称为兄弟结点(必须是亲兄弟),如上图: B、C 是兄弟结点。
结点的层次:从根开始定义起,根为第 1 层,根的子结点为第 2 层,以此类推。
树的高度或深度:树中结点的最大层次,如上图:树的高度为4。
结点的祖先:从根到该结点所经分支上的所有结点,如上图: A 是所有结点的祖先。
路径:一条从树中任意节点出发,沿父结点 - 子节点连接,达到任意节点的序列,比如A到Q的路径为: A-E-J-Q、H到Q的路径H-D-A-E-J-Q。
子孙:以某结点为根的子树中任一结点都称为该结点的子孙,如上图:所有结点都是A的子孙。
森林:由m(m>0)棵互不相交的树的集合称为森林。
(三)树的表示方法——孩子兄弟表示法:
树形结构相对于线性表来说就比较复杂了,要存储表示起来就比较麻烦,既需要保存值域,也要保存结点和结点之间的关系,这应该怎么表示?
方法很多,聪明的前辈们想出了一个非常天才的表示方法——孩子兄弟表示法。
我们定义一个树的结构体——
struct TreeNode
{ struct Node* child; // 左边开始的第⼀个孩⼦结点 struct Node* brother; // 指向其右边的下⼀个兄弟结点 int data; // 结点中的数据域
};
比如说下面这幅图中的树结构:
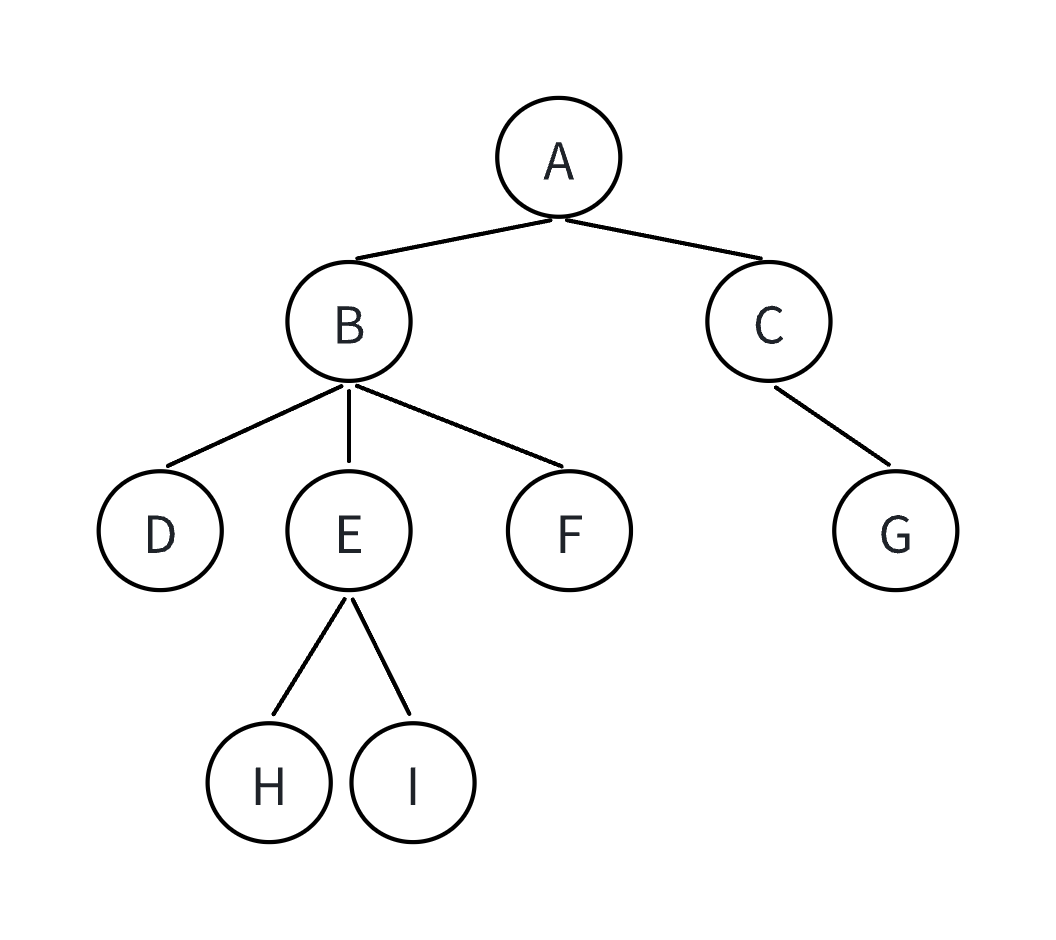
我们用孩子兄弟表示法可以这样表示——
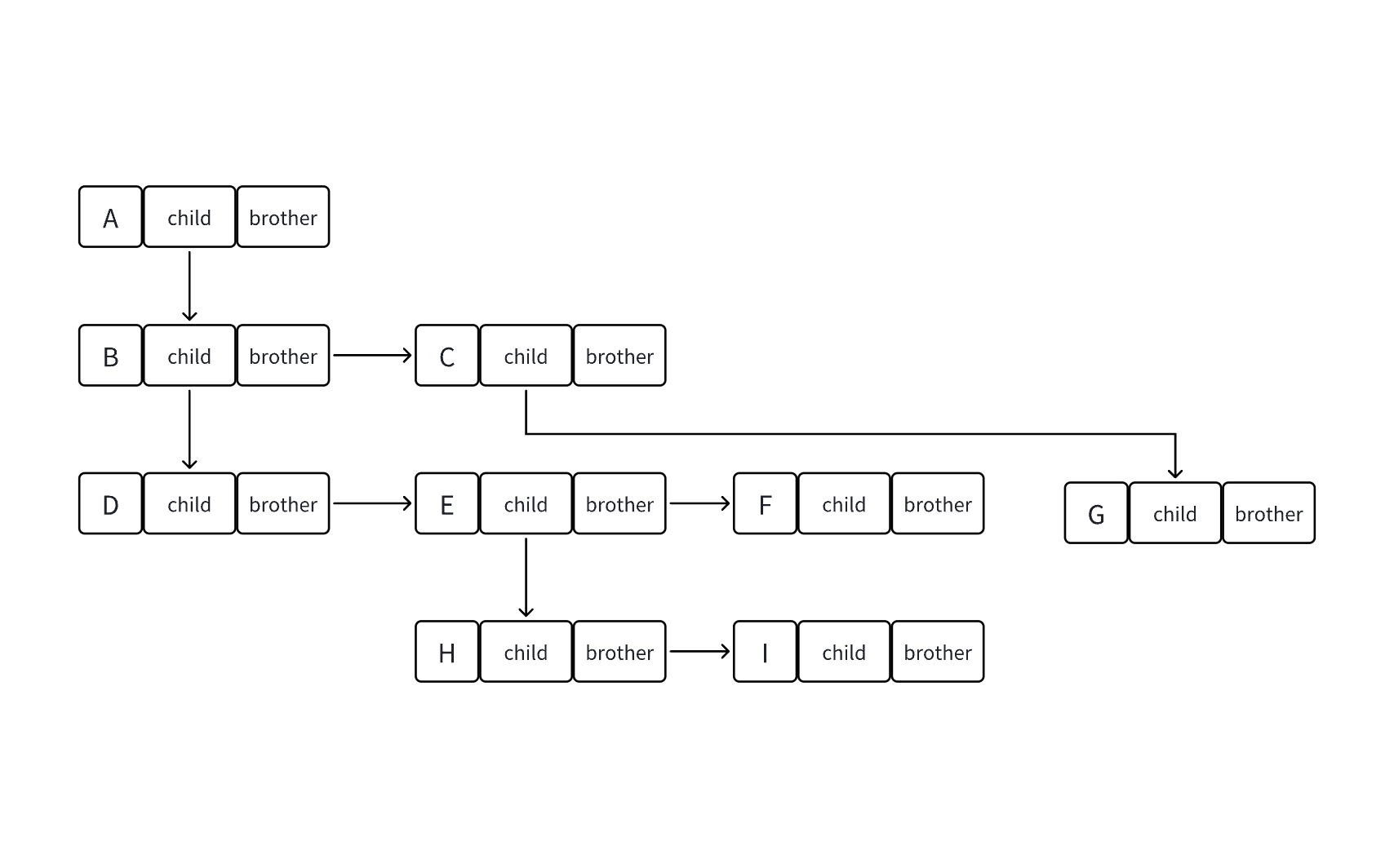
(四)树的实际应用场景
文件系统是计算机存储和管理文件的一种方式,它利用树形结构来组织和管理文件和文件夹。
在文件系统中,树结构被广泛应用,它通过父节点和子节点之间的关系来表示不同层级的文件和文件夹之间的关联。
比如我们【此电脑】里面的【设备和驱动器】——

比如我们的系统资源管理——
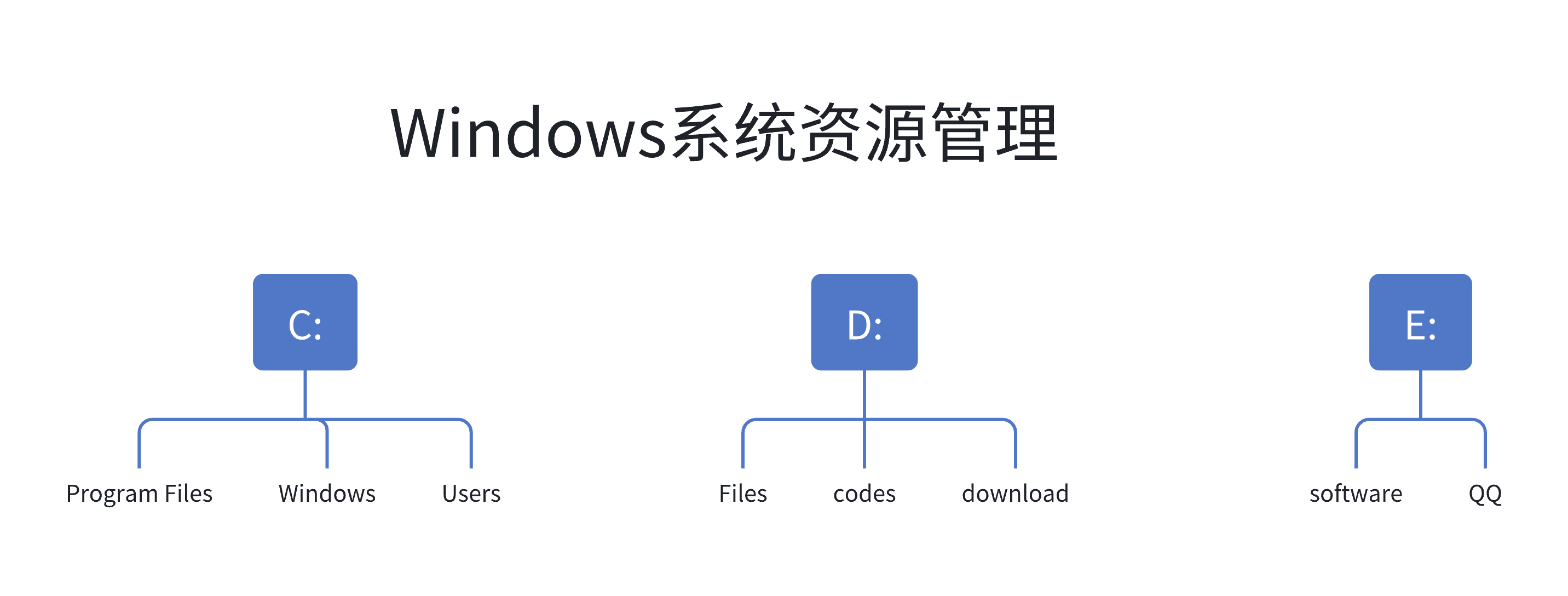
二、二叉树
(一)二叉树的概念与结构
1、概念
在树形结构中,我们最常用的就是二叉树,一棵二叉树是结点的一个有限集合,该集合由一个根结点加上两棵别称为左子树和右子树的二叉树组成或者为空。
2、结构
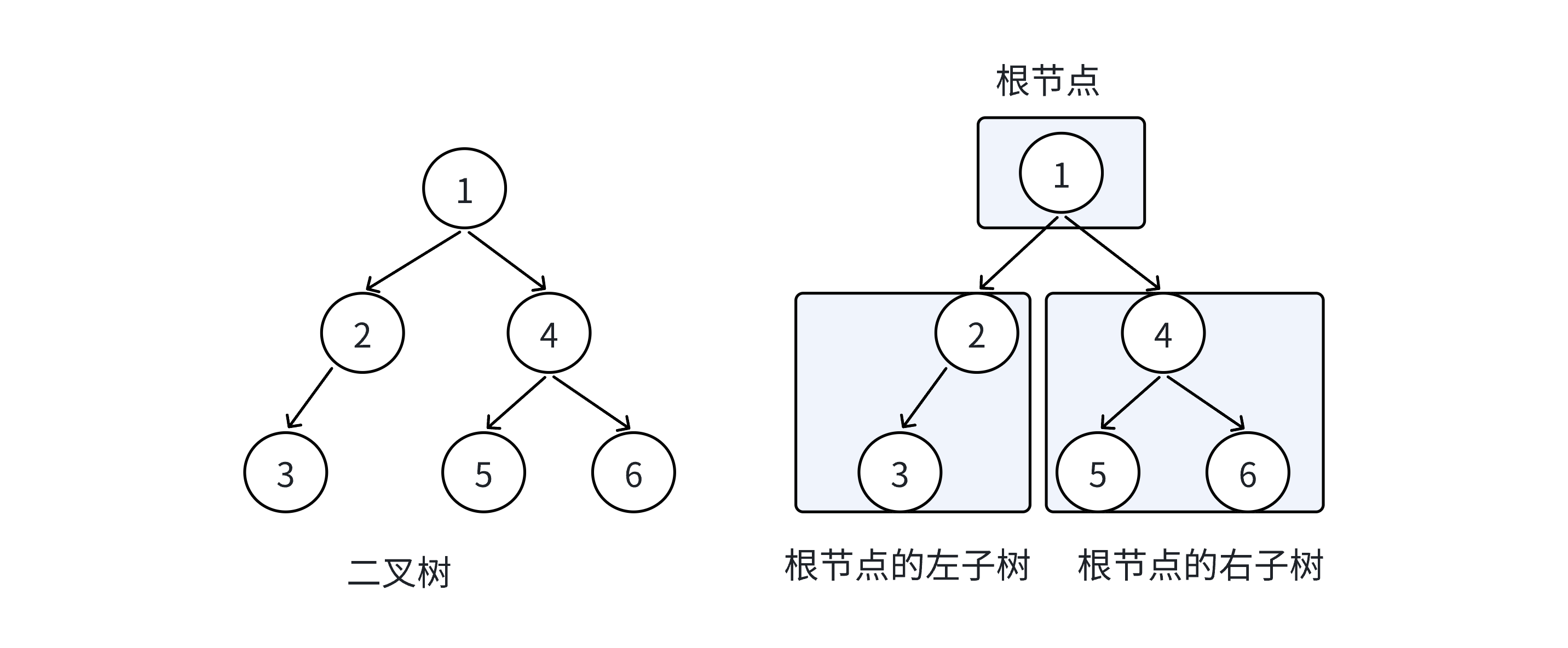
二叉树具备的特点:
1、二叉树不存在度大于2的结点(0、1、2);
2、二叉树有左右之分,次序不能颠倒,因此二叉树是有序树。
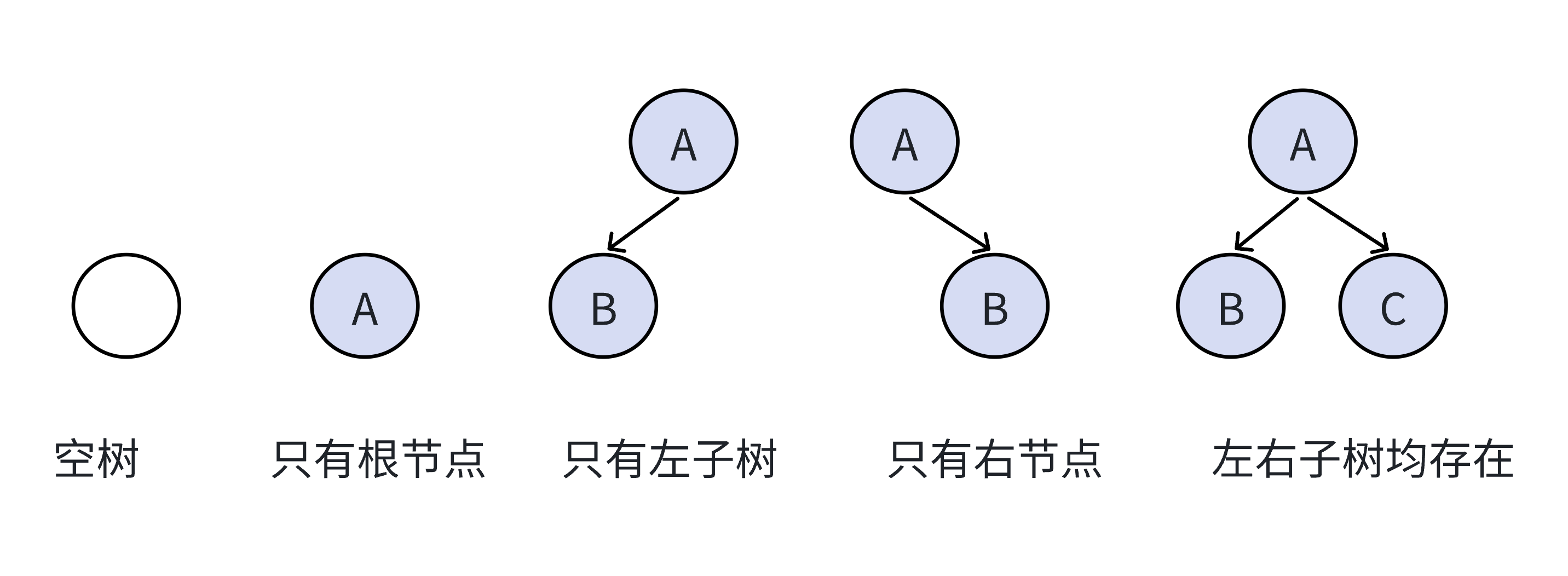
二叉树的结构非常多,比如下面这些,都是二叉树——
注意:对于任意的二叉树都是由以下几种情况复合而成的——
因此二叉树不是很好驾驭,于是我们定义了特殊的二叉树,比如满二叉树、完全二叉树等。
(二)一些特殊的二叉树
1、满二叉树
树->二叉树->特殊的二叉树->满二叉树
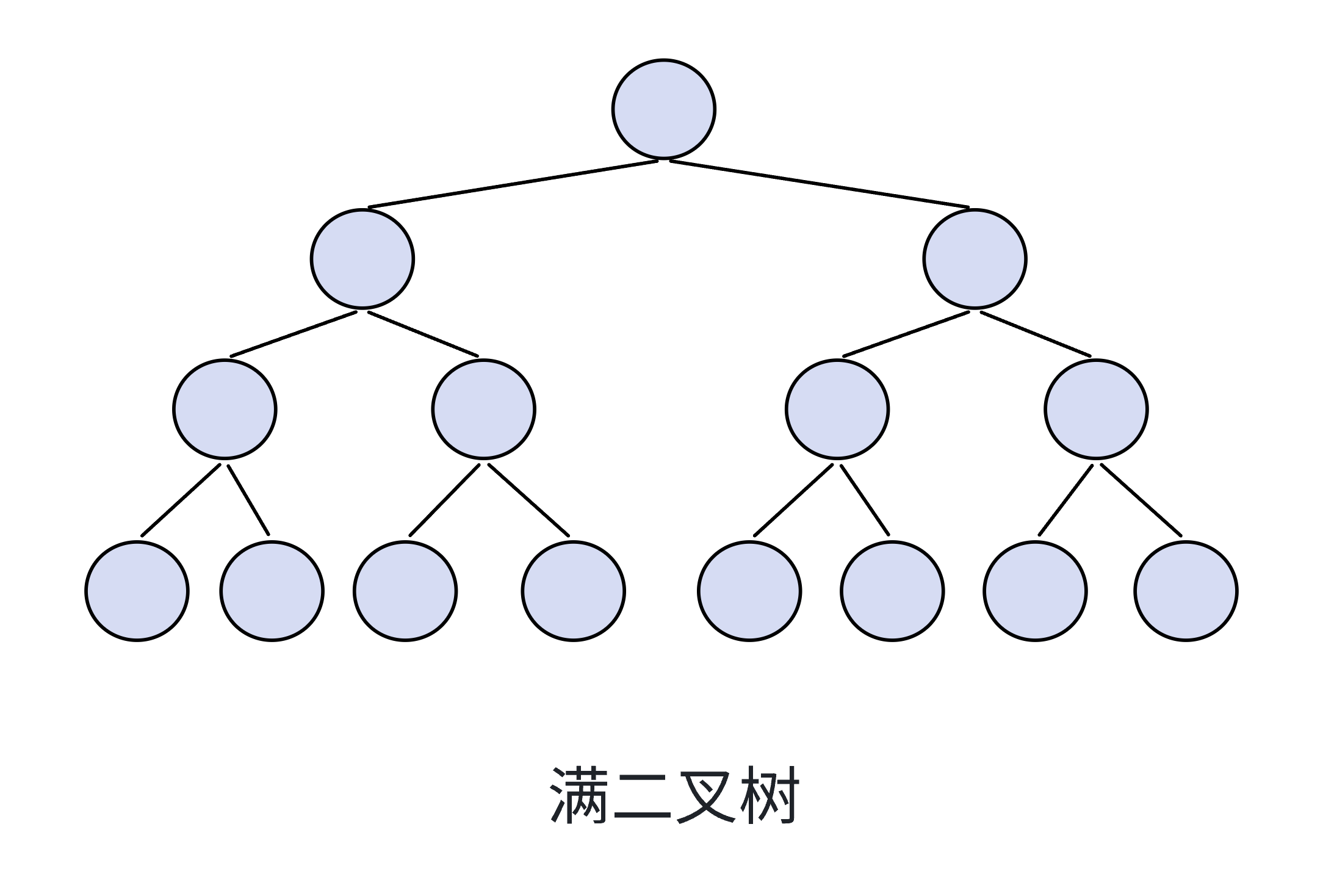
满二叉树(度为2,即最大结点个数为2),每一层结点数都最大,层数为K,结点总数为2^(k-1),这就是满二叉树。
1 1 2^02 2 2^13 4 2^24 8 2^3. . .. . .. . .k 2^(k-1) 2^(k-1)
层数 度问:总的结点个数是多少?
即让你求2^0 + 2^1 + 2^2 + 2^3 + .... + 2^(k-1) = ?。
我们想到等比数列求和公式,Sn——
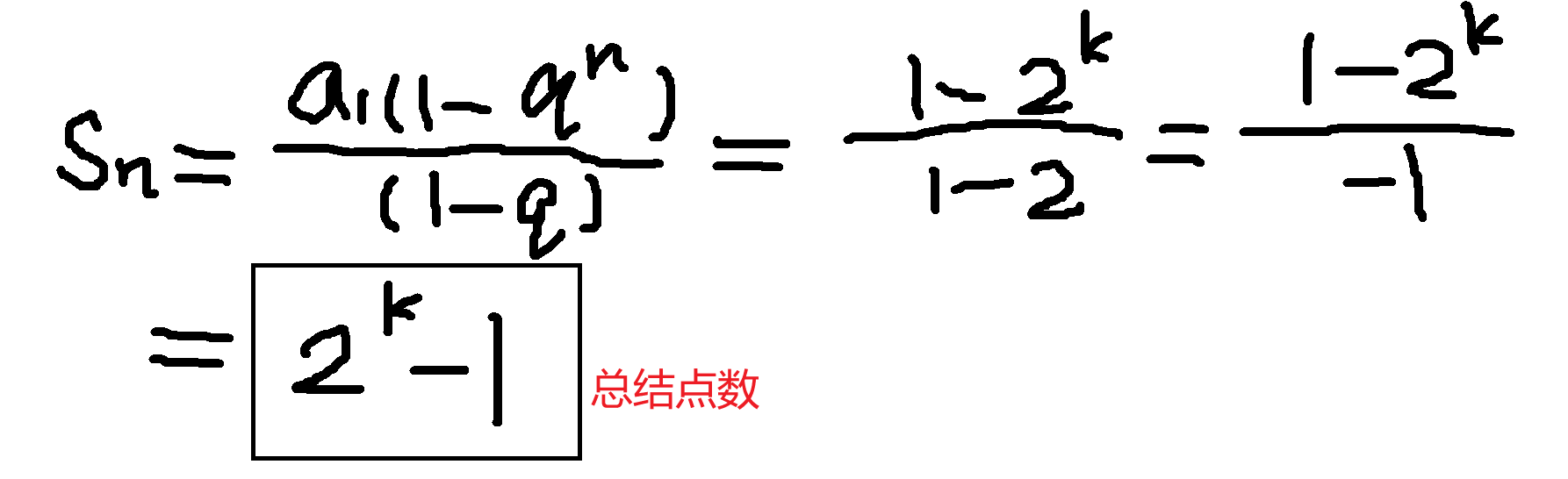
2、完全二叉树
完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。
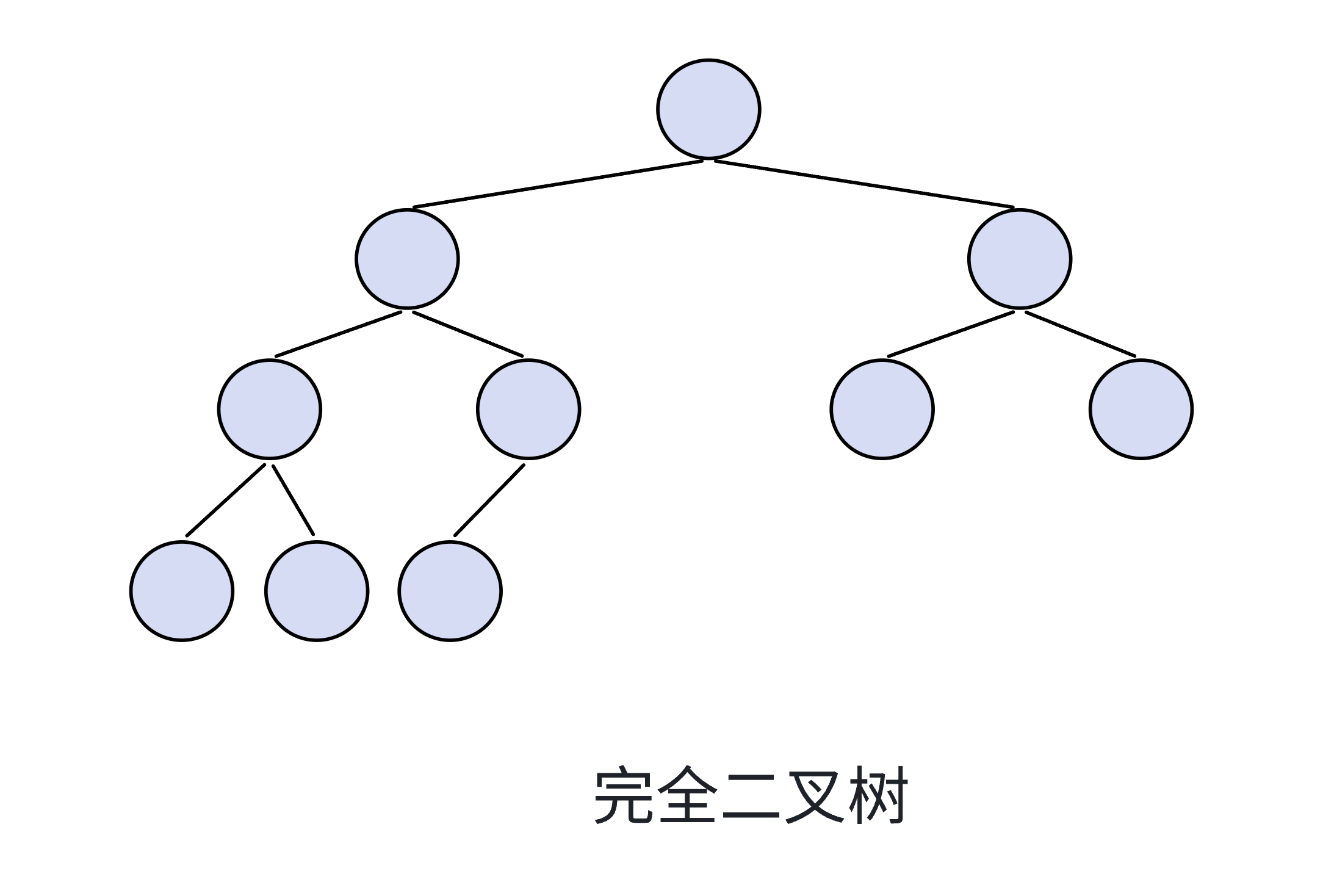

满二叉树是一种特殊的完全二叉树。
完全二叉树这个数据结构效率很高。
除了最后一层(叶子结点),其他每层结点个数都达到最大,最后一层不一定能达到最大(有可能达到,也可能达不到)——
达到了——满二叉树;达不到——完全二叉树。
满二叉树是完全二叉树的一种,也就是说:满二叉树既是完全二叉树,也是满二叉树(似废话)。
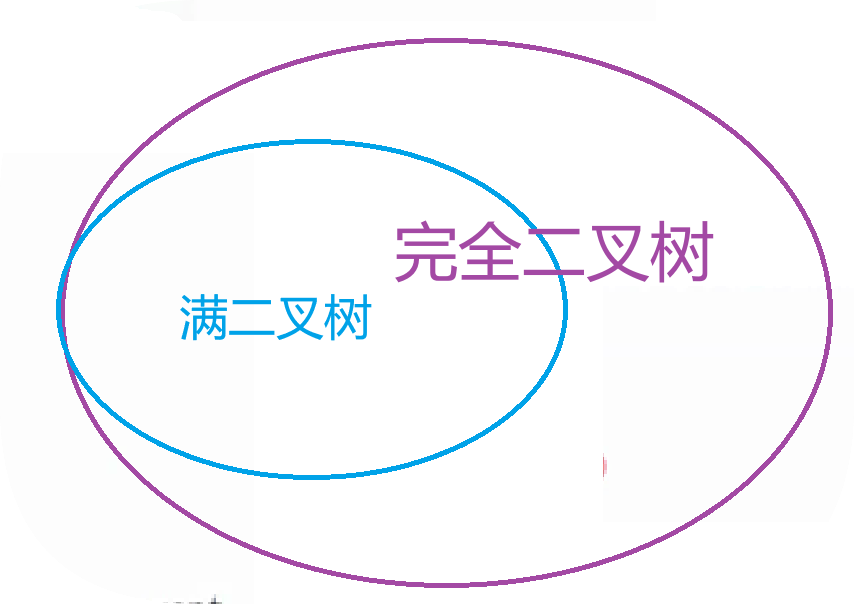
完全二叉树的结点是从左往右依次排列的——
这是非常重要的一个知识点,观察下图,是不是一个完全二叉树——
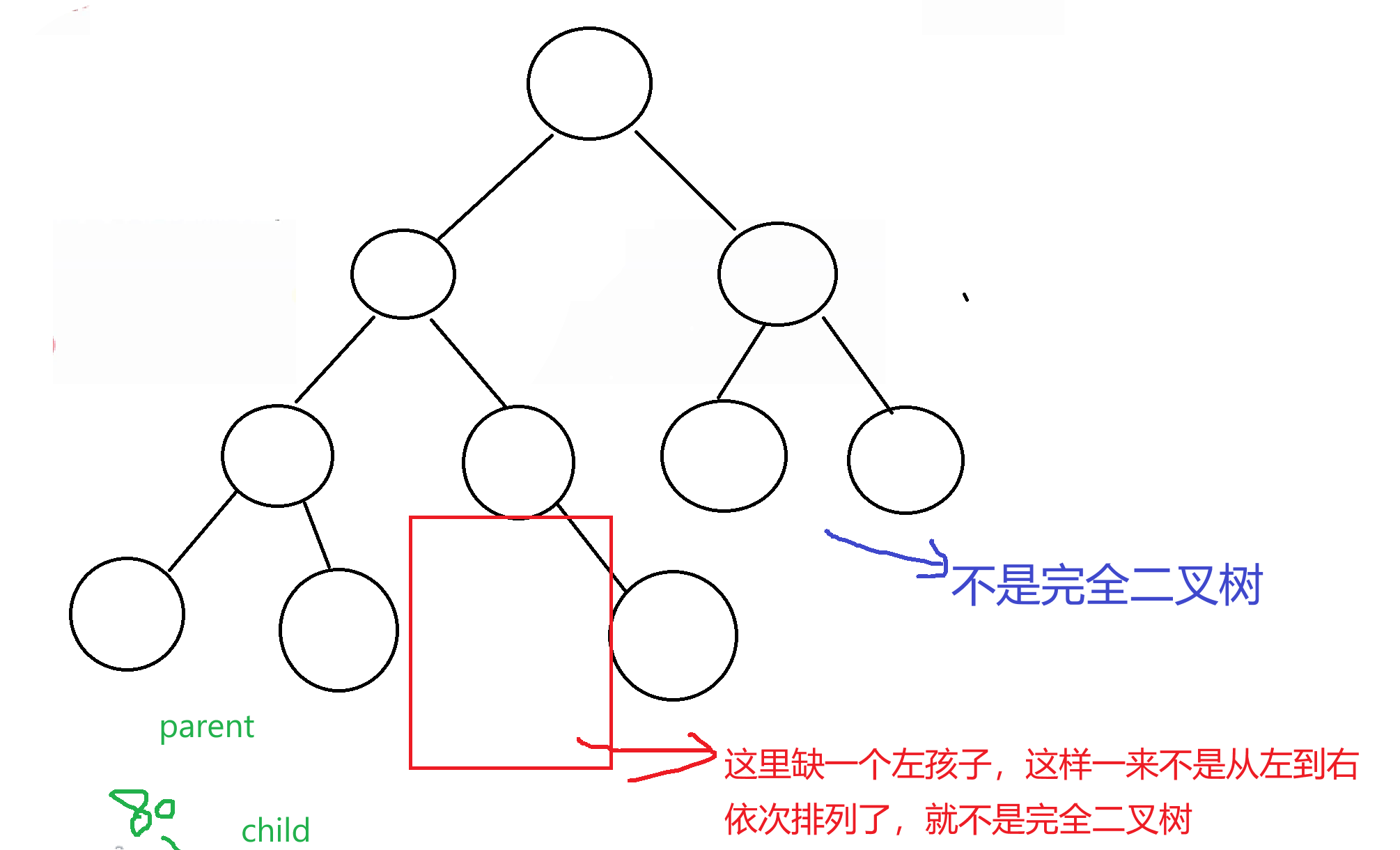
缺一个左孩子,这样一来不是从左到右依次排列了,就不是完全二叉树
3、二叉树存储结构
二叉树一般可以使用两种结构存储,一种顺序结构,一种链式结构。
(1)顺序结构
顺序结构存储就是使用数组来存储,一般使用数组只适合表示完全二叉树,因为不是完全二叉树会有空间的浪费,完全二叉树更适合使用顺序结构存储。
我们通常把堆(一种二叉树)使用顺序结构的数组来存储,需要注意的是这里的堆和操作系统虚拟进程地址空间中的堆是两回事,一个是数据结构,一个是操作系统中管理内存的一块区域分段。
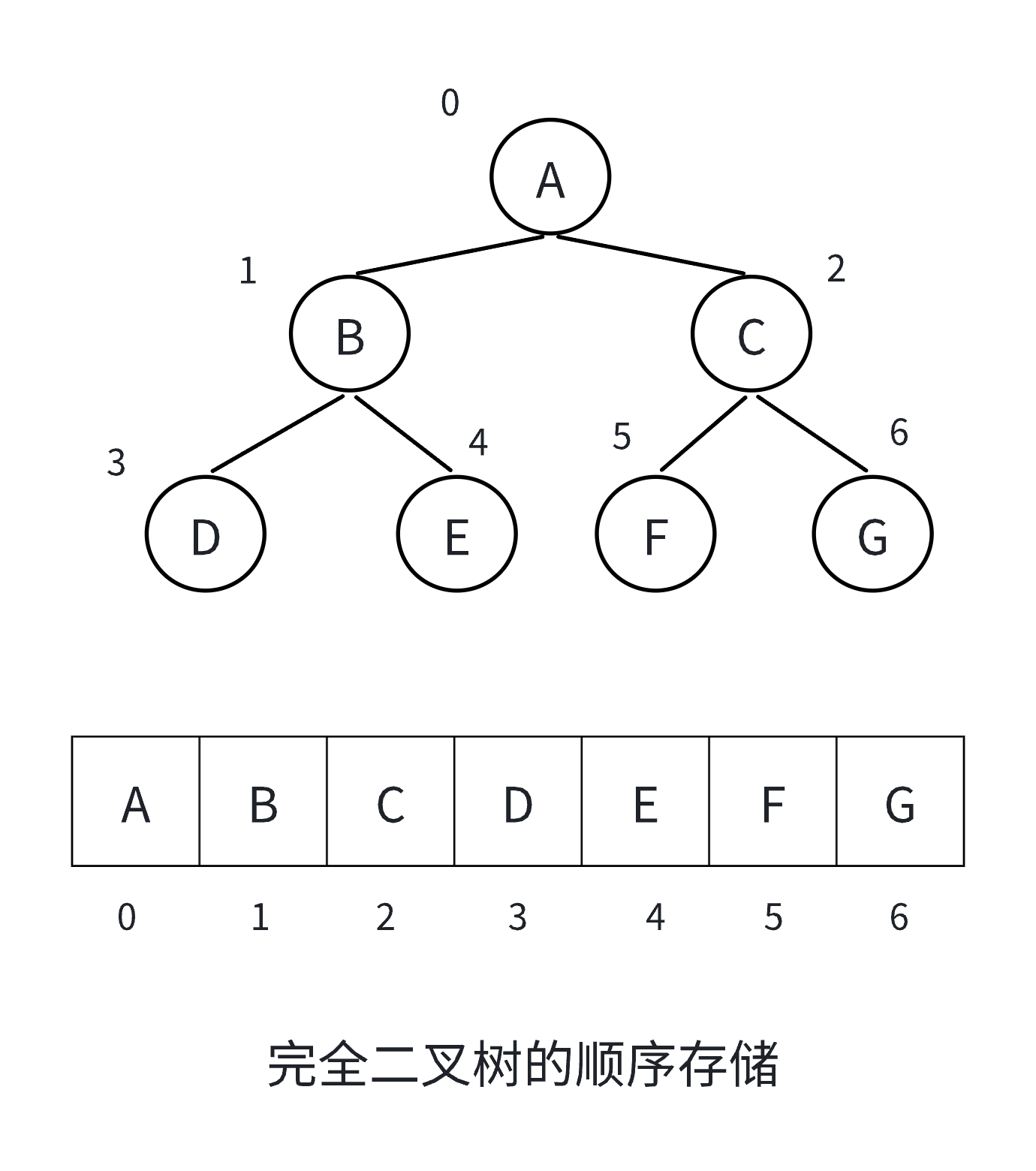
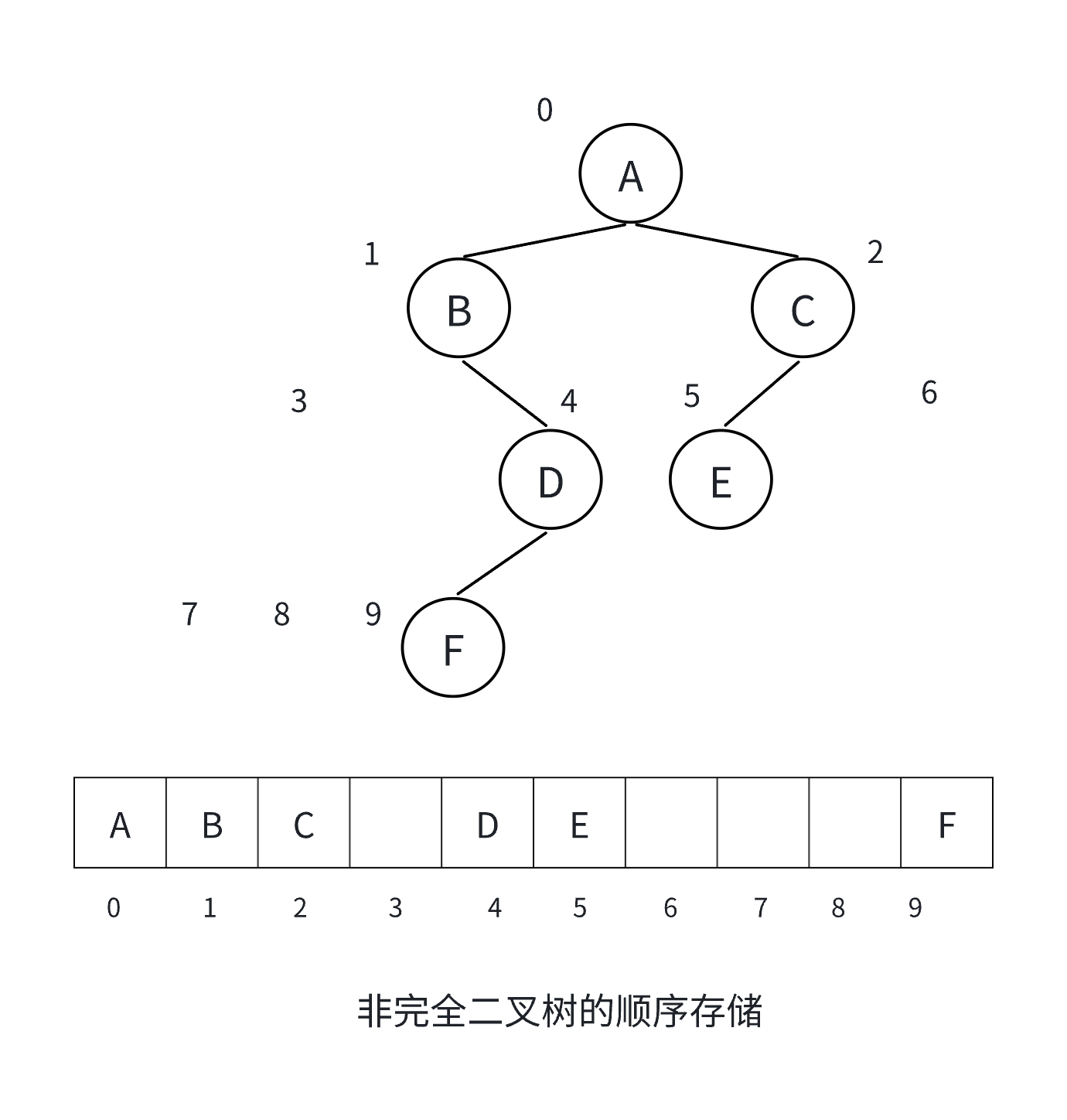
(2)链表结构
二叉树的链式存储结构是指,用链表来表示一棵二叉树,即用链来指示元素的逻辑关系。
通常的方法是链表中每个结点由三个域组成,数据域和左右指针域,左右指针分别用来给出该结点左孩子和右孩子所在的链结点的存储地址。
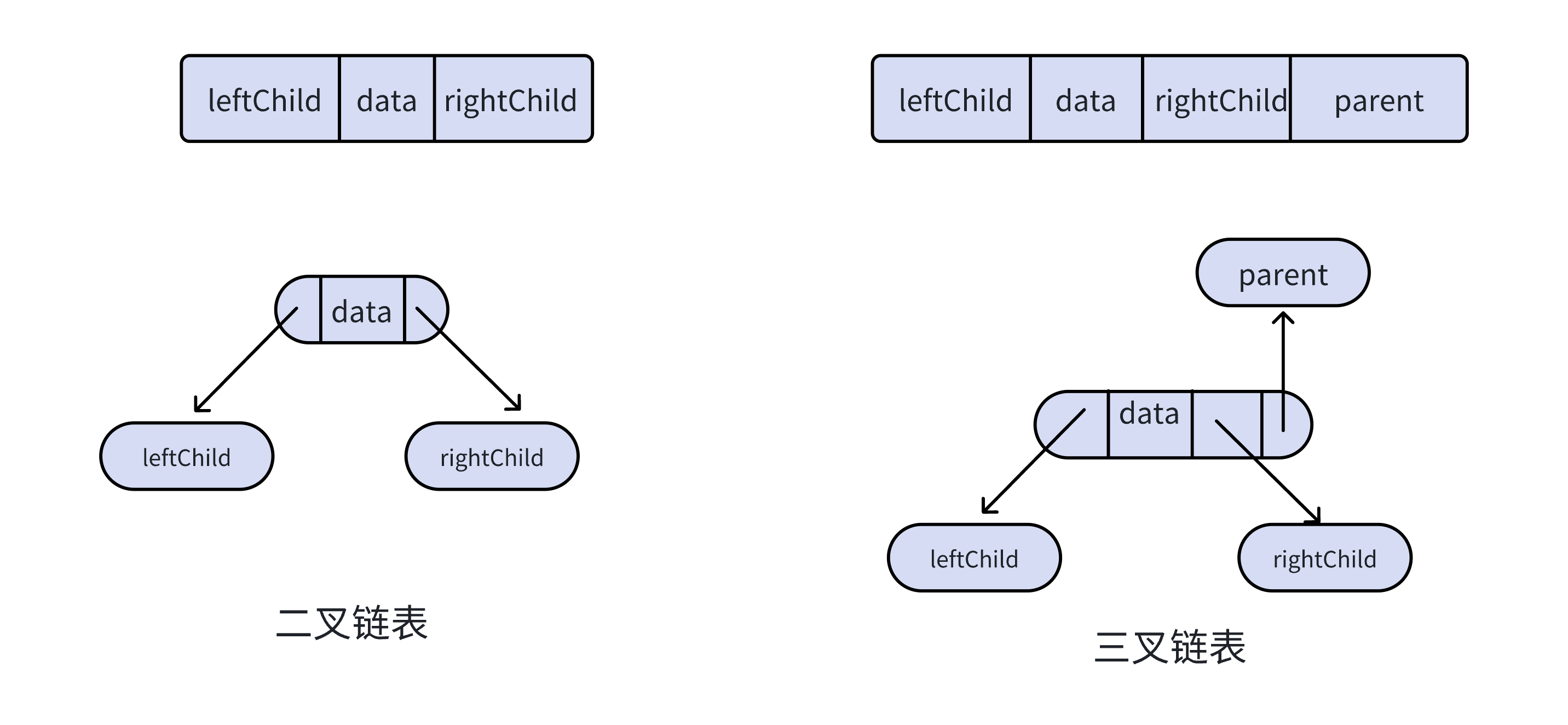
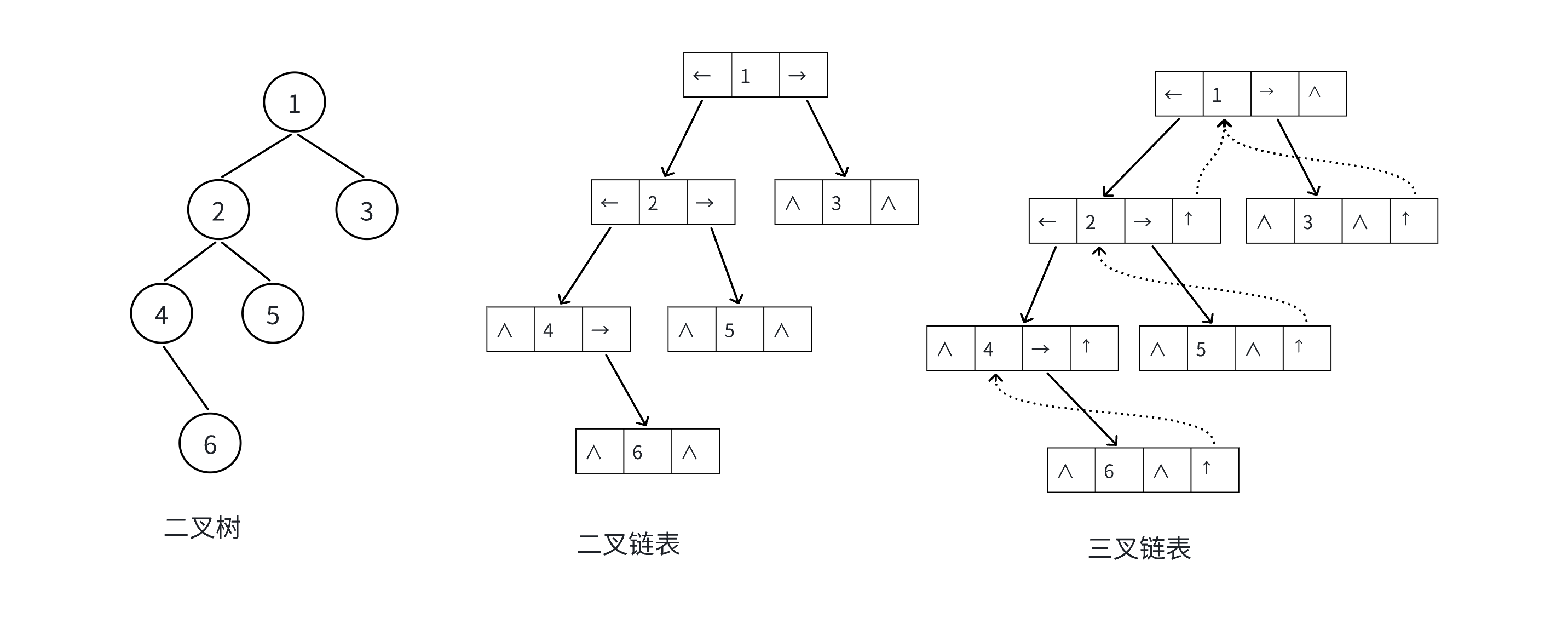
链式结构又分为二叉链和三叉链,当前我们学习中一般都是二叉链。后面博主等专栏(大概率会收录在新的C++专栏里面)更新到高阶数据结构如红黑树等会用到三叉链。
结尾
函数栈帧的创建与销毁相关博客的链接博主已经放在正文前面了,有需要自取。
往期回顾:
【数据结构与算法】数据结构初阶:详解栈和队列(下)——队列
【数据结构与算法】数据结构初阶:详解栈和队列(上)——栈
【数据结构与算法】数据结构初阶:详解顺序表和链表(五)——双向链表
【数据结构与算法】数据结构初阶:详解顺序表和链表(四)——单链表(下)
【数据结构与算法】数据结构初阶:详解顺序表和链表(三)——单链表(上)
本期内容需要回顾的C语言知识如下面的截图中所示(指针博主写了6篇,列出来有水字数嫌疑了,就只放指针第六篇的网址,博主在指针(六)把指针部分的前五篇的网址都放在【往期回顾】了,点击【传送门】就可以看了)。
大家如果对前面部分的知识点印象不深,可以去上一篇文章的结尾部分看看,博主把需要回顾的知识点相关的博客的链接都放在上一篇文章了,上一篇文章的链接博主放在下面了:
【数据结构与算法】数据结构初阶:详解顺序表和链表(三)——单链表(上)
结语:本篇文章到这里就结束了,对数据结构的二叉树知识感兴趣的友友们可以在评论区留言,博主创作时可能存在笔误,或者知识点不严谨的地方,大家多担待,如果大家在阅读的时候发现了行文有什么错误欢迎在评论区斧正,再次感谢友友们的关注和支持!