相似度计算
相似度计算是分类和聚类算法的前提
优秀的算法将类间的距离分的非常大,而类内的距离很小
欧几里得距离
欧式距离(Euclidean distance)是最常见、最直观的“直线距离”度量方式。它来源于欧几里得几何,用来计算两个点之间的“最短路径”长度。
数学定义
二维平面:两点 P(x_1, y_1) 与 Q(x_2, y_2) 的欧式距离
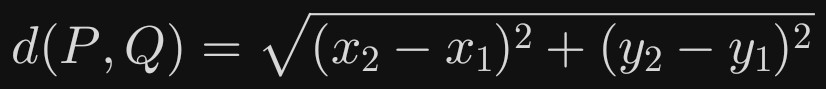
n 维空间:向量 X=(x_1,…,x_n) 与 Y=(y_1,…,y_n)
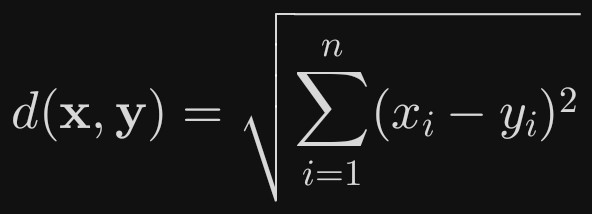
应用场景
KNN、K-means:样本相似度度量。
SLAM、机器人:路径规划中的“实际直线”距离。
图像处理:像素级差异度量(如 PSNR)。
推荐系统:把用户/物品嵌入向量后计算距离。
曼哈顿距离
曼哈顿距离(Manhattan Distance),又叫出租车几何(Taxicab Geometry)或 L1 距离,是衡量两点在“网格”状空间里沿轴对齐路径最短距离的一种方式。直观地讲,它模拟了在棋盘格城市(如纽约曼哈顿)里,出租车只能沿着水平和垂直街道行驶,而不能斜穿街区时,从 A 到 B 需要走过的街区总数。
数学定义
对于 n 维空间中的两点
P = (p₁, p₂, …, pₙ)
Q = (q₁, q₂, …, qₙ)
曼哈顿距离为:
D₁(P, Q) = Σᵢ |pᵢ − qᵢ|
应用场景
高维稀疏数据(文本 TF-IDF、推荐系统)
需要轴对齐可解释性的场景(如特征工程、规则系统)
对异常值更鲁棒,计算比欧氏距离更快(无平方、开方)
A* 寻路、网格地图上的启发函数 h(n) 常用曼哈顿距离(若只能四向移动)
切比雪夫距离
切比雪夫距离(Chebyshev distance,也叫 L∞ 距离或棋盘距离)是度量两个向量之间差异的一种“最极端”方式
数学定义
对于 n 维空间中的两个点
P = (p₁, p₂, …, pₙ)
Q = (q₁, q₂, …, qₙ)
其切比雪夫距离
d∞(P, Q) = maxᵢ |pᵢ − qᵢ|
应用场景
棋盘/网格路径规划(A*、Dijkstra 用切比雪夫启发式)。
某些鲁棒优化问题:当系统对“最坏维度误差”敏感时,用 L∞ 作为损失。
数字图像处理中的膨胀、腐蚀算子(最大滤波器)。
聚类或 k-NN 中,当特征量纲差异很大且只关心“有没有维度严重偏离”时,L∞ 可避免被小尺度维度主导。
闵可夫斯基距离
闵可夫斯基距离(Minkowski Distance)是一类通用的距离度量,它把许多我们熟悉的距离公式统一成一个带参数的“家族”。
数学表达
给定两个 n 维向量x = (x₁, x₂, …, xₙ)
y = (y₁, y₂, …, yₙ)
闵可夫斯基距离定义为
Dₚ(x, y) = (∑ᵢ |xᵢ − yᵢ|ᵖ)^(1/p) (p ≥ 1)
其中 p 是一个可调的超参数。
家族成员速览
p = 1:曼哈顿距离(L₁)
城市街区式的“只能走格子”路径长度。
p = 2:欧氏距离(L₂)
我们日常直觉里的“直线距离”。
p → ∞:切比雪夫距离(L∞)
只关注差异最大的那一维:maxᵢ |xᵢ − yᵢ|。
直观理解
把 p 想成“对差异的敏感度”:
p 越小,越“平等”地对待每一维的差异;
p 越大,越“放大”最大差异维度的影响。
应用场景
机器学习特征缩放:不同 p 的选择会改变聚类或 k-NN 对特征重要性的权衡。
异常检测:p 较大时,异常值对距离贡献更突出。
图像/信号处理:根据噪声维度特性选择合适的 p,调节对局部或全局差异的敏感度。
马哈拉诺比斯距离
马哈拉诺比斯距离(Mahalanobis Distance)可以一句话概括为:“考虑了变量相关性的加权欧氏距离”。它比普通的欧氏距离更聪明,能纠正不同尺度、不同相关性的变量带来的偏差。
数学定义
给定一个随机向量 X in Rp 和其分布的协方差矩阵 S(正定),与均值向量 mu的马氏距离为:若 S 是单位矩阵(变量独立且方差相等),则退化为欧氏距离。若变量尺度不同或存在相关性, S-1会“修正”这些影响。
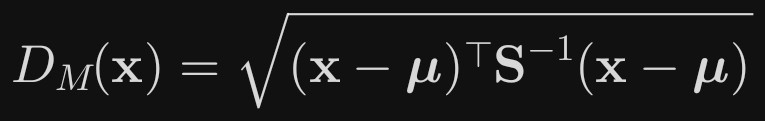
马氏距离里对“尺度差异”的修正,和标准化(比如Z-score标准化)的思路很像,都是为了消除变量单位和数值范围不同带来的影响。
不过马氏距离更进一步:标准化只能处理尺度差异,而马氏距离通过 \mathbf{S}^{-1} 还能同时消除变量间的相关性(比如身高和体重的正相关),这是它比“先标准化再算欧氏距离”更全面的地方。
应用场景
异常检测:识别多维数据中的离群点(如工业传感器数据)。
分类:如二次判别分析(QDA)中,用马氏距离衡量样本到各类的分布差异。
聚类:K-means++初始化时用马氏距离避免“维度灾难”。
皮尔逊相关系数
皮尔逊相关系数(Pearson Correlation Coefficient)是一种用于衡量两个变量之间线性相关程度的统计指标,通常用符号 r 表示。
数学定义
皮尔逊相关系数( r )的数学表达式如下:
对于两个变量 X 和 Y ,其样本皮尔逊相关系数为:
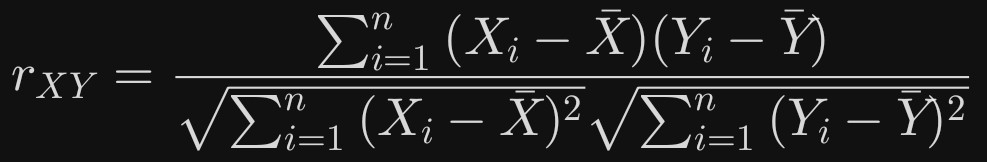
核心特点
取值范围:介于 -1 到 1 之间。
r = 1:完全正相关(一个变量随另一个变量同步递增)。
r = -1:完全负相关(一个变量随另一个变量同步递减)。
r = 0:无线性相关(但可能存在非线性关系)。
适用条件:
两个变量需为连续型数据(如身高、温度等)。
变量间关系近似线性。
数据大致符合正态分布。
应用场景
用于衡量两个连续变量之间的线性相关程度,其应用场景广泛,核心是判断变量间是否存在线性关联及关联强度。
余弦相似度
余弦相似度(cosine similarity)是一种衡量两个向量方向相近程度的无量纲指标。它把向量想象成从原点出发的箭头,只关心夹角,不关心长度,因此特别适合那些“频率”“权重”会被整体放缩的场景,比如文本、推荐系统或深度学习中的高维表征。
数学定义
给定两个非零向量 A、B,其余弦相似度定义为
cos(θ)= (A·B) / (‖A‖‖B‖) = Σᵢ AᵢBᵢ / √(ΣᵢAᵢ²) √(ΣᵢBᵢ²)
结果落在 [-1, 1]:
1 表示方向完全一致;
0 表示正交、无相关性;
-1 表示方向完全相反。
应用场景
文本:把文档变成 TF-IDF 或嵌入向量,用余弦相似度做检索、聚类、去重。
推荐:用户或物品的 embedding 向量,计算“兴趣接近度”。
深度学习:对比学习(如 SimCLR)用余弦相似度拉近正样本、推远负样本。
图像/音频:特征向量归一化后,用余弦距离(1-相似度)做匹配。
汉明距离
汉明距离(Hamming distance)是一种衡量两个等长字符串(或更一般的,两个等长符号序列)差异的度量方式。
它定义为:在相同位置上符号不同的总个数。
数学定义
对于两个向量 x, y in Sigman( Sigma 是符号集合),汉明距离为:
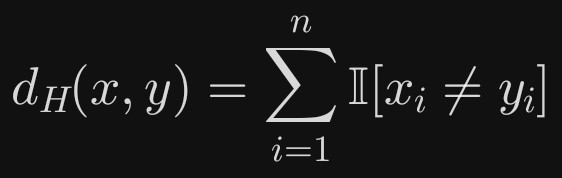
其中 I 是指示函数,条件成立时取1,否则取0。
应用场景
纠错码:如海明码(Hamming code)利用汉明距离检测并纠正单个比特错误。
信息检索:快速比对指纹、哈希值或二进制特征向量。
生物信息学:比较基因序列的相似性。
机器学习:用于分类任务中的k-NN算法(如文本分类中的词袋模型)。
KL散度
KL 散度(Kullback-Leibler divergence,记作 KL(P‖Q))是信息论里用来衡量“两个概率分布 P 与 Q 的差异”的一种非对称度量。它不是数学意义上的距离,而是一种“信息损失”或“惊讶度差”的量化方式——用来实现描述分布的差异
直观含义
把 P 当成真实分布、Q 当成近似分布。从 P 里采样一个事件 x,用 Q 去描述它时需要的“额外比特数”就是 log( P(x)/Q(x) )。对所有 x 取期望,就得到 KL(P‖Q)。
若 Q 与 P 完全一致,额外比特数为 0;
若 Q 在某些 P 高频的区域概率过低,KL 会很大。
数学定义
离散形式
KL(P‖Q)=∑ₓ P(x) log( P(x)/Q(x) )
连续形式
KL(P‖Q)=∫ p(x) log( p(x)/q(x) ) dx
约定:0 log(0/q)=0,p log(p/0)=+∞(Q 的支撑集必须覆盖 P 的支撑集)。
KL(P‖Q) ≠ KL(Q‖P),因此不对称,也不满足三角不等式。
应用场景
变分推断:ELBO 中的 −KL(q‖p) 项,迫使变分分布 q 靠近先验 p;
生成模型:VAE 用 KL(q(z|x)‖p(z)) 做正则;策略优化:RL 里的 TRPO、PPO 用 KL 约束策略更新幅度;
领域自适应:最小化源域与目标域特征分布的 KL;
特征选择 / 聚类:衡量变量分布变化,筛选信息量大的特征。
海林格距离
海林格距离(Hellinger distance)是用来衡量两个概率分布之间“差异”的一种度量,它介于 0 和 1 之间,越接近 0 表示两个分布越相似,越接近 1 表示差异越大。
数学定义
对两个概率密度函数(或概率质量函数)p 与 q,海林格距离定义为:
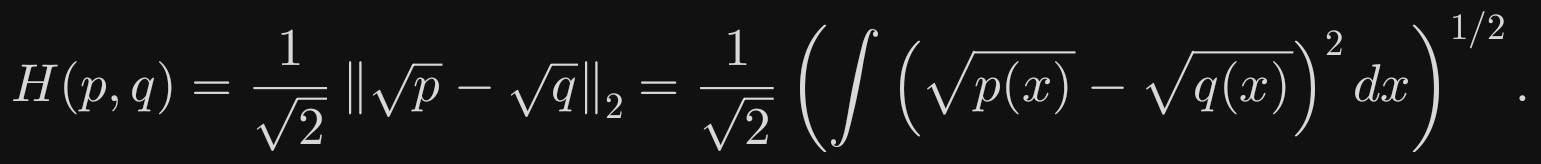
离散情形把积分换成求和即可。
更常用的是平方形式
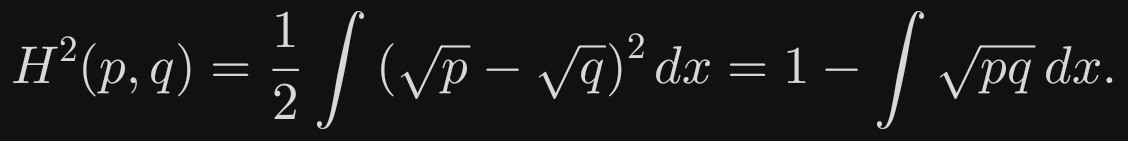
特点
对概率密度开平方,让差异更“温和”(避免极端值主导)。
1/sqrt(2) 和外面的根号:是为了让距离满足数学上“距离”的性质(比如非负、对称、三角不等式),相当于标准化系数。
最后一项称为 Bhattacharyya 系数,介于 0 与 1。
应用场景
非参数贝叶斯:在 Dirichlet 过程、Pitman–Yor 过程等模型中,Hellinger 距离常被用来度量后验收缩速度。
鲁棒统计:相比 KL 散度,它对模型误设更稳健。
生成模型评估:作为 GAN 或 VAE 中真实分布与生成分布的差异度量之一。
聚类与分类:在概率分布空间上定义“样本”之间的距离,再使用 k-means、核方法等。
编辑距离
编辑距离(Edit Distance)是衡量两个字符串之间“差异度”的一种量化指标,也叫 Levenshtein Distance(列文斯坦距离)。它定义为:将一个字符串转换成另一个字符串所需的最少“编辑操作”次数。
允许的编辑操作
- 插入(Insertion):在任意位置插入一个字符。
- 删除(Deletion):删除任意一个字符。
- 替换(Substitution):将任意一个字符替换成另一个字符。
例子
比较字符串
kitten 和 sitting:kitten → sitten (k → s,替换)
sitten → sittin (e → i,替换)
sittin → sitting (末尾插入 g,插入)共 3 次操作
因此它们的编辑距离为 3。
计算方式
编辑距离通常用 动态规划 计算。设 dp[i][j] 表示字符串 a[0…i-1] 与 b[0…j-1] 的编辑距离,状态转移方程为:
if a[i-1] == b[j-1]:dp[i][j] = dp[i-1][j-1] # 字符相同,无需操作
else:dp[i][j] = 1 + min(dp[i-1][j], # 删除 a[i-1]dp[i][j-1], # 插入 b[j-1]dp[i-1][j-1] # 替换 a[i-1] 为 b[j-1])
应用场景
拼写纠错(如搜索引擎的“您是不是想找…”)
DNA 序列比对(生物信息学)
版本控制系统(如 Git 的 diff 算法)
语音识别(匹配声学模型输出与词典词条)
