后来者居上与先来后到：栈和队列的顺序哲学及算法实战（含源码）

---

栈的概念

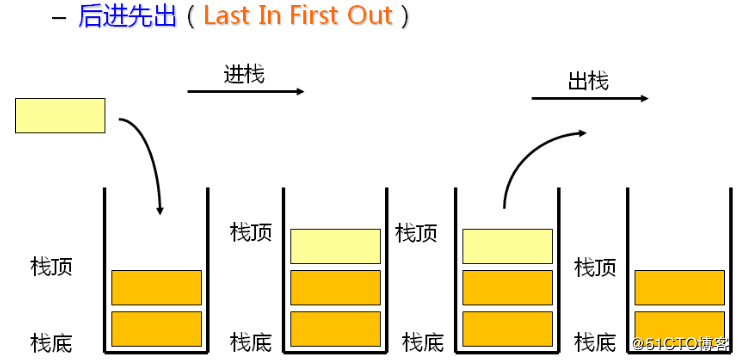
   栈：一种特殊的线性表，其只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端称为栈顶，另一端称为栈底（不做任何操作）。栈中的数据元素遵守后进先出LIFO（Last In First Out）的原则。

       上述是官方堆栈的基本介绍，下面我通过画图的方式给大家介绍下在栈中进行插入和删除数据。

        插入数据有个专业名字叫压栈或者进栈/入栈，入数据是在栈顶。

       删除数据同样有专有名词叫出栈，可以理解为把数据从栈中拿出，同样也是在栈顶进行操作，因为栈底根据下图可以发现是封住的，只有栈顶有开口，方便进出数据。

       我们不断的进出栈，发现我们后进栈的数据在最上面，所以我们先要拿走的数据也是最上面的，因此可得入栈和出栈满足后进先出的规律，可以理解成后来者居上

栈底层结构的选择

       思考：栈既然是线性表的一种，在逻辑结构上则一定是线性的，那么在物理结构上是线性的还是非线性的呢？

       这个问题的实质就是我们是使用数组还是链表构造栈，数组则是：一定是线性的，链表则是不一定是线性的。

  首先申明：栈使用链表和数组均可实现

1 . 用链表实现栈时，若头结点位置是栈顶、尾节点位置是栈底，增删数据（操作栈顶）很快，时间复杂度是 O (1)，但是使用链表需要不断移动指针来确定栈顶和栈底的位置。

2 . 用数组实现栈就简单多了，把 a [0] 设为栈底后，这个位置就不用改了。栈顶的增删操作因为数组地址连续，不用遍历，只需要size++/- -，消耗成本更低，时间复杂度也是 O (1)。

数组实现：

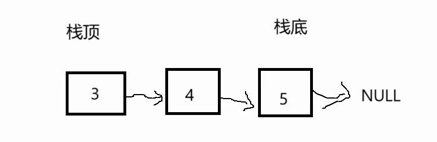
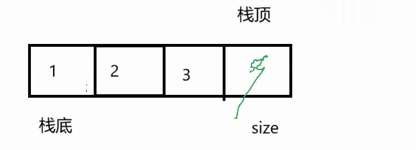
链表实现：

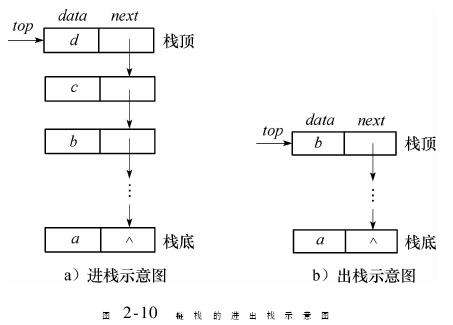
结论：因此更推荐使用数组实现栈

二、栈的实现

1. 栈的定义

       这里定义栈和顺序表类似，将顺序表中的size换了个名字为top（作用一样）表示栈顶

typedef int STDataType;
//定义栈的数据结构
typedef struct Stack
{STDataType* arr;int top;//指向栈顶的位置int capacity;
}ST;

2. 初始化

      1.需要断言，检査的是传入的队列指针本身是否为NULL，防止空指针接音乐

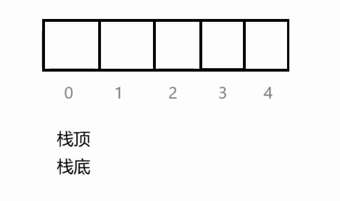
      2.在初始化时，栈中没有任何数据，栈顶和栈底位置均在a[0]处

void STInit(ST* ps)
{assert(ps);ps->arr = NULL;ps->capacity = ps->top = 0;
}

3. 销毁

      既然创建了栈就要回收进行销毁，这里和顺序表链表代码原理一样（可以看我之前的博客），不进行过多介绍

void STDestroy(ST* ps)
{if (ps->arr != NULL)free(ps->arr);ps->arr = NULL;}

4. 入栈

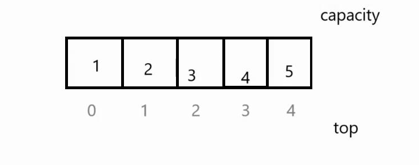
      1.初始情况下栈为空，数组需要申请空间，也就需要判断空间是否足够，当top等于capacity时栈满了（初始情况下top在a[0]处，每插入一个数据，top++）就需要增容，这里防止增容失败将原来数据弄丢定义临时变量保证安全

      2.增容成功后赋值，将要插入的数据放到top++位置

void  StackPush(ST* ps, STDataType x)
{assert(ps);if (ps->capacity == ps->top){//空间满了--增容int newcapacity = ps->capacity == 0 ? 4 : 2 * ps->capacity;STDataType* tmp = (STDataType*)realloc(ps->arr,newcapacity*sizeof(STDataType));if (tmp == NULL){perror("realloc fail!\n");exit(1);}ps->arr = tmp;ps->capacity = newcapacity;}//空间足够ps->arr[ps->top++] = x;
}

5. 判断栈是否为空

1 . 定义bool类型的函数判断栈是否为空
2.需要断言空指针
3.如果top（栈顶）位置为0，则栈为空返回true，否则返回false

bool StackEmpty(ST* ps)
{assert(ps);return ps->top == 0;
}

6. 出栈

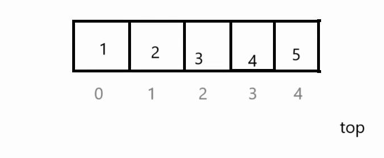
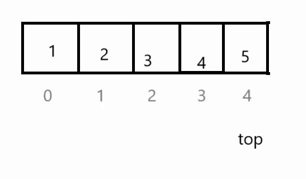
     出栈需要考虑到栈是否为空，为空则不能删除数据，即top为0时不能继续减了，不为空直接让top自减即可。

     在下图中原本栈中有五个数据，删除一个数据后，top在a[4]位置，栈中只有四个有效数据1,2，3,4，其中5不包含在内，如果后面要插入数据在top位置插入数据即可（若插入数据6，那么把原来的5覆盖即可）

void  StackPop(ST* ps)
{assert(!StackEmpty(ps));--ps->top;}

7. 取栈顶元素

     取栈顶元素和出栈很类似，但是要注意的是出栈直接top- -，不知道原来的栈顶元素是什么，但是取栈顶这个方法是知道栈顶元素的。

     这里还是要判断栈是否为空，为空栈顶元素不存在，无法取，若存在我们直接返回数组中arr[top-1]位置的数据，如下图，栈顶元素为5

STDataType StackTop(ST* ps)
{assert(!StackEmpty(ps));return ps ->arr[ps->top - 1];
}

8.获取栈中有效元素个数

     我们发现top位置下标的数据就是栈中现有的数据个数，如下图，top为5，那么栈中存放了5个有效数据

int STSize(ST* ps)
{assert(ps);return ps->top;}

三、与栈相关的简单OJ题

有效的括号

题目解释： 题目给定来判断字符串是否有效需要满足的三个定义，

1. 若有左括号必须有与其对应的有右括号，这很好理解，如有“（” 则必须有 “）”，有“ [ ”则必须有“ ] ”,具体可以借鉴示例1和3
2. 正确的顺序我们可以借鉴示例4发现，先存放了“（”后存放“ [ ”,但是对应的“ ] ”却是先出现，而“）”是后出现，我们通过案例发现先进后出的规律，这与我们学习的栈是否有关系呢？
3. 初次看这个条件我们感觉与条件1不就是一样的吗？为啥还需多此一举呢，但我们仔细想想发现除了满足条件1下还有个细节：如果没有左括号，仅有右括号字符串也无效

经过上述题目描述我们明确了使用数据结构——栈可以解决该题目，那么我们如何根据栈的入栈和出栈特性来定义左括号和右括号?我们可以定义变量pi遍历字符串，遇到左括号就入栈，遇到右括号就取栈顶元素检查是否是与之对应的右括号。在进行上述过程中我们发现如果是有效字符串，取完栈顶元素后，栈为空 ，下面是临界条件的判断：

   如果pi与栈顶元素不匹配，则该字符串不是有效的，如“{ ( } ) [ ]”
   取栈顶元素时若栈顶为空，即只有右括号，该字符串不是有效的括号，如“） ”

   若字符串遍历完不为空，只有左括号，同样不是有效的，如“ { ”

   代码思路：pi遍历字符串直至到“\0”结束，如果pi遍历到的是“[” ,“{”,"("的其中一个便入栈，如果不是则判断栈是否为空，为空返回false，不为空判断栈顶是否与pi位置的括号是相对应的，不是继续返回false，是则取栈顶元素，然后继续让pi++。最后退出循环，判断栈是否为空，为空则是有效的，不为空是无效的

代码如下

typedef char STDataType;
//定义栈的数据结构
typedef struct Stack
{STDataType* arr;int top;//指向栈顶的位置int capacity;
}ST;//初始化
void STInit(ST* ps)
{assert(ps);ps->arr = NULL;ps->capacity = ps->top = 0;
}//销毁
void STDestroy(ST* ps)
{if (ps->arr != NULL)free(ps->arr);ps->arr = NULL;}//入栈
void  StackPush(ST* ps, STDataType x)
{assert(ps);if (ps->capacity == ps->top){//空间满了--增容int newcapacity = ps->capacity == 0 ? 4 : 2 * ps->capacity;STDataType* tmp = (STDataType*)realloc(ps->arr,newcapacity*sizeof(STDataType));if (tmp == NULL){perror("realloc fail!\n");exit(1);}ps->arr = tmp;ps->capacity = newcapacity;}//空间足够ps->arr[ps->top++] = x;
}//判断栈是否为空bool StackEmpty(ST* ps)
{assert(ps);return ps->top == 0;
}//出栈--栈顶
void  StackPop(ST* ps)
{assert(!StackEmpty(ps));--ps->top;}//取栈顶元素
STDataType StackTop(ST* ps)
{assert(!StackEmpty(ps));return ps ->arr[ps->top - 1];
}//获取栈中有效元素个数
int STSize(ST* ps)
{assert(ps);return ps->top;}
bool isValid(char* s) {//思路：借助数据结构-栈，遇到左括号就入栈，遇到右括号就取栈顶元素检查是否是与之对应的右括号ST st;STInit(&st);char *pi=s;while(*pi!='\0'){if(*pi=='('||*pi=='['||*pi=='{'){//入栈StackPush(&st,*pi);}else{//取栈顶，判断//1.若栈顶为空，即没有右括号，该字符串不是有效的括号//2.若字符串遍历完，栈不为空，该字符串不是有效的括号//如果栈为空if(StackEmpty(&st)){return false;}//栈不为空char top=StackTop(&st);if((top=='('&&*pi!=')')||(top=='['&&*pi!=']')||(top=='{'&&*pi!='}')){STDestroy(&st);return false;}StackPop(&st);}pi++;}/*if(StackEmpty(&st)){return true}else{return false;}*/bool ret=StackEmpty((&st))?true:false;STDestroy(&st);return ret;
}

     注意：我们使用的是C语言，由于之前我们手动实现了栈，这里直接调用即可，如果说是java或C++直接调用即可，不需要这么麻烦

四、队列的概念

     队列：只允许在一端进行插入数据操作，在另一端进行删除数据操作的特殊线性表，队列具有先进先出FIFO(First In First Out) 。

     我们发现队列和栈不同之处在于，栈只有一段开口，插入和删除均在栈顶实现，而队列则是两端开口，但是我们规定了：一端只能插入数据，一端只能删除数据，如下图

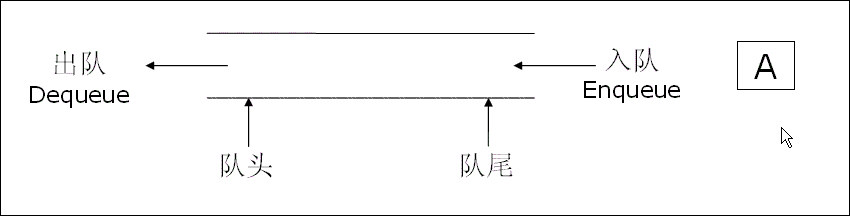
     入队列：进行插入操作的一端称为队尾

     出队列：进行删除操作的一端称为队头

     在上图中我们发现先进队列的数据先出队列，后进队列的后出来，满足先进先出原则，可以理解成先来后到

队列底层结构的选择

     这里我们和栈一样要对队列底层结构是使用数组还是链表进行判断。

     假设我们使用数组来构造，因为入数据尾插简单，我们先假设数组末端为队尾，那么a[0]位置就是队头，入数据我们发现时间复杂度为O(1)，但是出数据我们把数据删除完后，还要将后面的数据往前移动，那么就需要遍历数组，时间复杂度为O（n）。所以我们放放弃使用数组构造

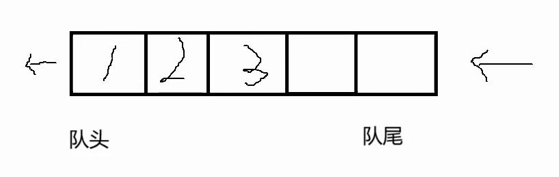
       那么我们使用链表构造呢？

        我们假设队头是链表头结点，入数据时间复杂度为O（1），那么队尾就是尾节点处，但是我们发现如果出数据，我们出去的数据在尾节点处，但是链表的地址不一定是连续的，那么我们就需要遍历链表的next节点来找尾节点，时间复杂度也为O（n）

       那么是否链表也不行呢？这里我们想到了如果我们使用双向链表是否可以呢？这里确实是可以的，时间复杂度为O(1),但是会有额外空间的消耗（要定义prev指针）。如果我们就想使用单链表那么该怎么办？

       这里我们让头结点为队头，出数据时间复杂度为O(1),尾节点为队尾,如果我们给尾节点是,链表我们已知有个phead指向头结点，那么我们可以给链表再加上个ptail指针指向尾节点，我们在尾节点后面插入数据，因为已知到尾节点，直接插入数据即可(尾节点的next指向newnode)，不需要遍历，时间复杂度为O(1)，

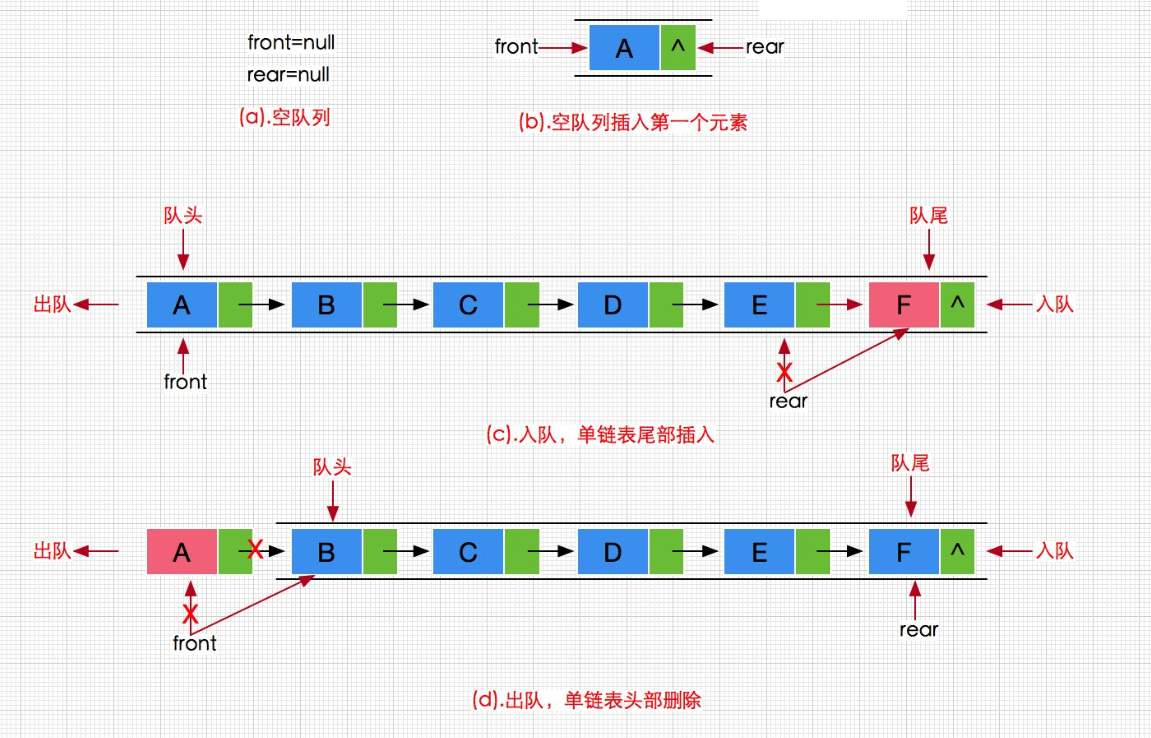
结论： 所以这里我们使用链表即可

五、队列的实现

1. 队列的定义

      队列是链表构成，链表是由一个个节点构成，因此我们先定义队列的节点结构，定义完了节点，我们还要针对队列要定义phead指向队头（头结点），，ptail指向队尾（尾节点），它们是节点结构类型的指针，如果不定义结构体就需要传二级指针了，比较麻烦

typedef int QDataType;
//定义队列节点的结构
typedef struct QueueNode
{QDataType data;struct QueueNode* next;}QueueNode;//定义队列的结构
typedef struct Queue
{QueueNode* phead;//队头：出数据QueueNode* ptail;//队尾：入数据int size;		//队列有效元素个数}Queue;

2. 初始化

      这里的初始化和链表的初始化原理相同，借鉴我之前博客解释即可

void QueueInit(Queue* pq)
{assert(pq);pq->phead = pq->ptail = NULL;pq->size = 0;
}

3. 队尾插入数据

      和链表插入数据原理类似，在队列为空下，让头节点和尾节点均指向newnode，不为空则我们要让ptail的next指向插入的节点，然后再让ptail走到新位置

//队尾插入数据
void QueuePush(Queue* pq, QDataType x)
{assert(pq);QueueNode* newnode = (QueueNode*)malloc(sizeof(QueueNode));if (newnode == NULL){perror("malloc fail!\n");exit(1);}newnode->data = x;newnode->next = NULL;//队列为空，队头和队尾都是newnodeif (pq->phead == NULL){pq->phead = pq->ptail = newnode;}else {//pq->ptail newnodepq->ptail->next = newnode;pq->ptail = pq->ptail->next;}pq->size++;
}

4. 队列判空

      只需要判断头结点是否为NULL，为空的话队列为空，否则不为空

bool QueueEmpty(Queue* pq)
{assert(pq);return pq->phead == NULL;}

5.队列有效元素个数

      我们发现想看队列中有多少个数据，需要遍历，那我们就定义个指针pcur初始下指向头结点，定义size，不为空就自增，时间复杂度为O(n)

      但是在之前的接口中我们发现时间复杂度均是O（1），那么我们思考是否可以优化代码让其复杂度降低呢？

      我们可以在定义队列的时候再定义size变量表示队列有效元素个数，若插入数据size++，出数据则size- -，在这里我们直接返回size大小即可

int QueueSize(Queue* pq)
{/*int size = 0;QueueNode* pcur = pq->phead;while (pcur){size++;pcur=pcur->next;}return size;*/return pq->size;}

6.队头删除数据

      在删除数据时我们要判断临界条件，
      1 . 如果队列中只有一个节点，删除后，队列就为空了，由于我们创建队列时malloc了空间，那么我们就需要释放，防止内存泄漏。
      2 . 如果不止一个元素元素时，需要保存phead->next的数据，不然删除完头结点数据后，无法找到下一个节点.
      删除完头结点数据后，让phead->next走到phead位置作为新的头结点

void QueuePop(Queue* pq)
{assert(pq);assert(! QueueEmpty(pq));//只有一个节点的情况if (pq->phead == pq->ptail)//这里有多种可能，可以是pq->phead->next=NULL,pq->ptail->next=NULL,size=1,pq->phead == pq->ptail{free(pq->phead);pq->phead = pq->ptail = NULL;}else{ //多个节点QueueNode* next = pq->phead->next;free(pq->phead);pq->phead = next;}pq->size--;}

7. 取队头元素

     1.断言判空
     2.定义了phead一直指向头结点，因此我们只需要找到phead里面存储的data即可

QDataType QueueFront(Queue* pq)
{assert(pq);assert(!QueueEmpty(pq));return pq->phead->data;
}

8 .取队尾元素

     1.断言判空
     2.返回ptail存储的data数据

QDataType QueueBack(Queue* pq)
{assert(pq);assert(!QueueEmpty(pq));return pq->ptail->data;}

9. 销毁队列

     1.断言防止队列指针传入空
     2.定义pcur初始下指向头结点，遍历队列
     3.定义next保存pcur的next节点后再释放pcur
     4.pcur为空后退出循环，让phead=ptail=NULL，size置为0

void QueueDestroy(Queue* pq)
{assert(pq);QueueNode* pcur = pq->phead;while (pcur){QueueNode* next = pcur->next;free(pcur);pcur = next;}pq->phead = pq->ptail = NULL;pq->size = 0;
}

六、栈和队列综合OJ题

1.用队列实现栈

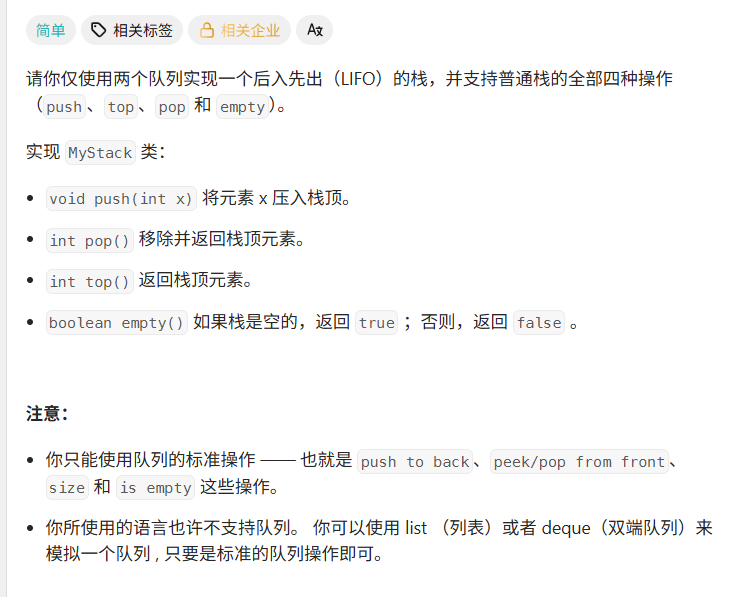
     题目解释： 使用两个队列结构实现栈的先进后出，并要支持栈的插入，删除，判空，返回栈顶元素的功能

     思考：
      我们发现如果我们使用之前OJ题的三指针反转队列的思路是可以实现这道题的，但是会把队列本身的性质给修改了，简单点理解就是队列自己的接口里面没有反转这个功能。

       这里我们又想到把两格队列给连接在一起，但是我们发现如果连接在一起就变成了一个队列，就违背了题目的条件。因此我们只能使用队列自己已有的接口来解决该题。

     思路： 1.入栈：往不为空的队列插入数据

                2.出栈：把不为空的队列中前size-1个数据挪到另一个队列中，不为空队列最后一个            元素出队列

                 3.取栈顶元素：取不为空队列中的队尾数据

代码实现：

typedef int QDataType;
//定义队列节点的结构
typedef struct QueueNode
{QDataType data;struct QueueNode* next;}QueueNode;//定义队列的结构
typedef struct Queue
{QueueNode* phead;//队头：出数据QueueNode* ptail;//队尾：入数据int size;		//队列有效元素个数}Queue;void QueueInit(Queue* pq)
{assert(pq);pq->phead = pq->ptail = NULL;pq->size = 0;
}//队尾插入数据
void QueuePush(Queue* pq, QDataType x)
{assert(pq);QueueNode* newnode = (QueueNode*)malloc(sizeof(QueueNode));if (newnode == NULL){perror("malloc fail!\n");exit(1);}newnode->data = x;newnode->next = NULL;//队列为空，队头和队尾都是newnodeif (pq->phead == NULL){pq->phead = pq->ptail = newnode;}else {//pq->ptail newnodepq->ptail->next = newnode;pq->ptail = pq->ptail->next;}pq->size++;
}//队列判空
bool QueueEmpty(Queue* pq)
{assert(pq);return pq->phead == NULL;}//队列有效元素个数
int QueueSize(Queue* pq)
{/*int size = 0;QueueNode* pcur = pq->phead;while (pcur){size++;pcur=pcur->next;}return size;*/return pq->size;}//队头删除数据
void QueuePop(Queue* pq)
{assert(pq);assert(! QueueEmpty(pq));//只有一个节点的情况if (pq->phead == pq->ptail)//这里有多种可能，可以是pq->phead->next=NULL,pq->ptail->next=NULL,size=1,pq->phead == pq->ptail{free(pq->phead);pq->phead = pq->ptail = NULL;}else{ //多个节点QueueNode* next = pq->phead->next;free(pq->phead);pq->phead = next;}pq->size--;}//取队头数据
QDataType QueueFront(Queue* pq)
{assert(pq);assert(!QueueEmpty(pq));return pq->phead->data;
}//取队尾数据
QDataType QueueBack(Queue* pq)
{assert(pq);assert(!QueueEmpty(pq));return pq->ptail->data;}//销毁队列
void QueueDestroy(Queue* pq)
{assert(pq);QueueNode* pcur = pq->phead;while (pcur){QueueNode* next = pcur->next;free(pcur);pcur = next;}pq->phead = pq->ptail = NULL;pq->size = 0;
}
///////////////////上面是队列以及相关的方法////////////////////////////////
typedef struct {Queue q1;Queue q2;
} MyStack;//栈的初始化
MyStack* myStackCreate() {MyStack*pst=(MyStack*)malloc(sizeof(MyStack));QueueInit(&pst->q1);QueueInit(&pst->q2);return pst;
}//入栈
void myStackPush(MyStack* obj, int x) {if(!QueueEmpty(&obj->q1)){QueuePush(&obj->q1,x);}else{QueuePush(&obj->q2,x);}
}//出栈
int myStackPop(MyStack* obj) {Queue*emp=&obj->q1;Queue*noneEmp=&obj->q2;if(QueueEmpty(&obj->q2)){emp=&obj->q2;noneEmp=&obj->q1;}//把noneEmp前size-1个数据导入到emp中while(QueueSize(noneEmp)>1){QueuePush(emp,QueueFront(noneEmp));QueuePop(noneEmp);}int top=QueueFront(noneEmp);QueuePop(noneEmp);return top;}//取栈顶元素
int myStackTop(MyStack* obj) {if(!QueueEmpty(&obj->q1)){return  QueueBack(&obj->q1);}else{return QueueBack(&obj->q2);}
}//判空
bool myStackEmpty(MyStack* obj) {//栈不为空则需要q1和q2队列均不为空return  QueueEmpty(&obj->q1)&&QueueEmpty(&obj->q2);
}void myStackFree(MyStack* obj) {QueueDestroy(&obj->q1);QueueDestroy(&obj->q2);free(obj);obj=NULL;
}/*** Your MyStack struct will be instantiated and called as such:* MyStack* obj = myStackCreate();* myStackPush(obj, x);* int param_2 = myStackPop(obj);* int param_3 = myStackTop(obj);* bool param_4 = myStackEmpty(obj);* myStackFree(obj);
*/

2. 用栈实现队列

     题目解释： 这里和上一题时类似，我们用栈的性质来实现队列的先进先出

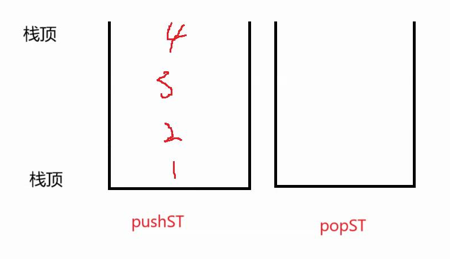
     思路： 入队列：往pushst栈中插入数据

                出队列：判断popst是否为空，不为空直接出数据（拿出来=删除数据），为空则将pushst中的数据全部导入到popst中（取pushst栈顶出栈然后入栈到popst中）

                取队头元素：判断popst是否为空，不为空直接取数据（不需要删除），为空则将pushst中的数据全部导入到popst中

代码实现：

typedef int STDataType;
//定义栈的数据结构
typedef struct Stack
{STDataType* arr;int top;//指向栈顶的位置int capacity;
}ST;
//初始化
void STInit(ST* ps)
{assert(ps);ps->arr = NULL;ps->capacity = ps->top = 0;
}//销毁
void STDestroy(ST* ps)
{if (ps->arr != NULL)free(ps->arr);ps->arr = NULL;}//入栈
void  StackPush(ST* ps, STDataType x)
{assert(ps);if (ps->capacity == ps->top){//空间满了--增容int newcapacity = ps->capacity == 0 ? 4 : 2 * ps->capacity;STDataType* tmp = (STDataType*)realloc(ps->arr,newcapacity*sizeof(STDataType));if (tmp == NULL){perror("realloc fail!\n");exit(1);}ps->arr = tmp;ps->capacity = newcapacity;}//空间足够ps->arr[ps->top++] = x;
}//判断栈是否为空bool StackEmpty(ST* ps)
{assert(ps);return ps->top == 0;
}//出栈--栈顶
void  StackPop(ST* ps)
{assert(!StackEmpty(ps));--ps->top;}//取栈顶元素
STDataType StackTop(ST* ps)
{assert(!StackEmpty(ps));return ps ->arr[ps->top - 1];
}//获取栈中有效元素个数
int STSize(ST* ps)
{assert(ps);return ps->top;}
////////////以上是栈的结构以及相关方法//////////////////
typedef struct {ST pushST;ST popST;
} MyQueue;MyQueue* myQueueCreate() {MyQueue*pq=(MyQueue*)malloc(sizeof(MyQueue));STInit(&pq->pushST);STInit(&pq->popST);return pq;
}void myQueuePush(MyQueue* obj, int x) {StackPush(&obj->pushST,x);
}int myQueuePop(MyQueue* obj) {if(StackEmpty(&obj->popST)){//把pushst中的数据全部导入到popst进来while(!StackEmpty(&obj->pushST)){StackPush(&obj->popST,StackTop(&obj->pushST));StackPop(&obj->pushST);}}int top=StackTop(&obj->popST);StackPop(&obj->popST);return top;}//取队头
int myQueuePeek(MyQueue* obj) {if(StackEmpty(&obj->popST)){//把pushst中的数据全部导入到popst进来while(!StackEmpty(&obj->pushST)){StackPush(&obj->popST,StackTop(&obj->pushST));StackPop(&obj->pushST);}}int top=StackTop(&obj->popST);// StackPop(&obj->popST);这里不需要出栈return top;
}bool myQueueEmpty(MyQueue* obj) {return StackEmpty(&obj->pushST)&&StackEmpty(&obj->popST);
}void myQueueFree(MyQueue* obj) {STDestroy(&obj->pushST);STDestroy(&obj->popST);free(obj);obj=NULL;
}/*** Your MyQueue struct will be instantiated and called as such:* MyQueue* obj = myQueueCreate();* myQueuePush(obj, x);* int param_2 = myQueuePop(obj);* int param_3 = myQueuePeek(obj);* bool param_4 = myQueueEmpty(obj);0 * myQueueFree(obj);
.3+1
12*/

3. 设计循环队列

循环队列的概念

     在解决这道题之前我们需要了解什么是循环队列，队列底层可以使用链表或者数组，而在之前的学习中我们知道循环链表如果尾节点不指向空，指向头结点那么就是循环链表。那么循环队列举一反三可得循环队列是首尾相连。

     循环队列成环，环形队列同样可以是使用数组或者链表均可以，具体如下图

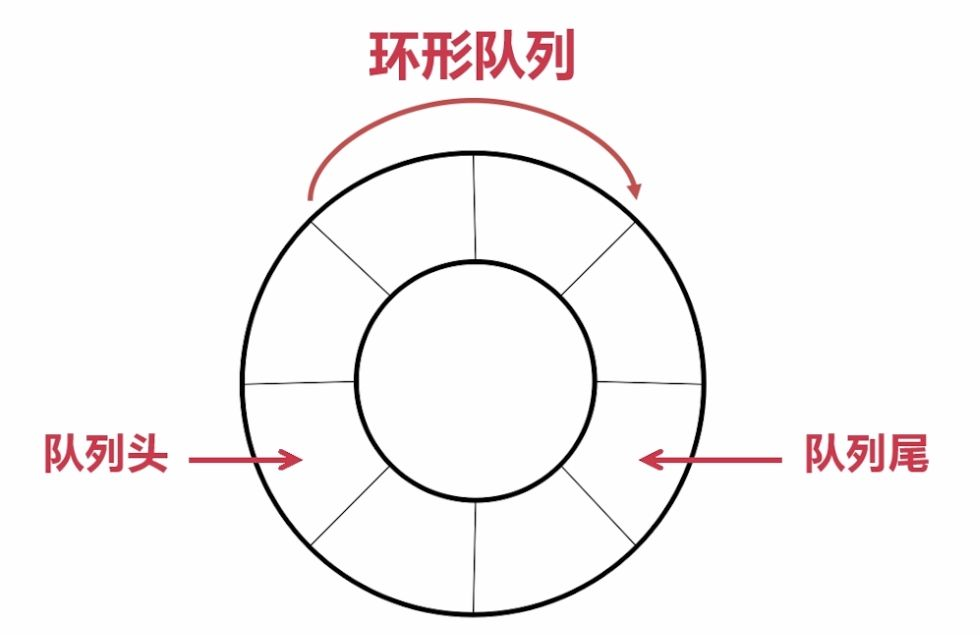
     题目解释： 这里我们需要用到题目中提到的循环队列的好处是可以利用这个队列之前用过的空间，所以我们可以得到以下的结论：
     1.循环队列满了，不能插入数据，即不能realloc
     2.删除数据的空间可以反复利用（不需要free还给操作系统）

     如果我们底层使用链表，会遇到下图找不到尾的窘境，删除phead存储的数据，那么phead就需要往后走走到了2的位置


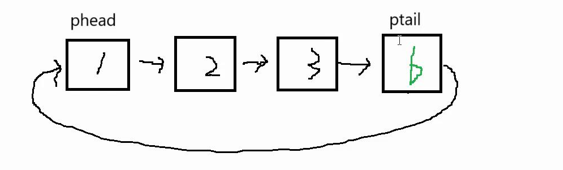
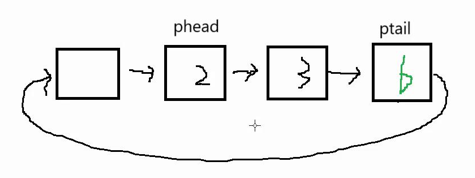
     那么如果我们要插入数据7，由于插入数据时队尾，所以我们要让ptail走到原本1的位置

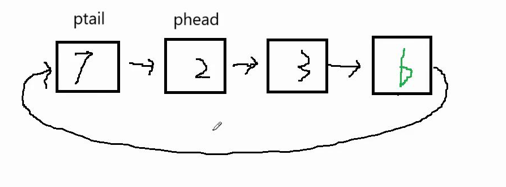
     如果我们又需要删除队头的数据，那么我们ptail就需要往回走，走到原来6的位置,我们发现使用单链表无法找到6的位置，那么我们就需要使用双向循环链表才行，比较麻烦

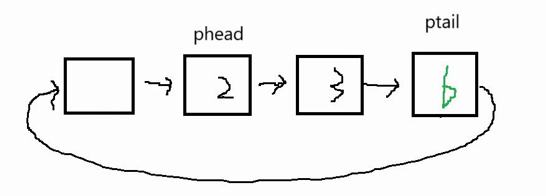
     因此我们假设使用数组来实现循环队列，如果我们要删除数据只需要让phead++即可，如果插入数据，在4的后面插5，我们让ptail往后走发现不能++，但是我们让ptail+1%数组的长度4=0，那么ptail就走到1的位置，我们在1的位置就可以插入5，如果ptail++可以往后走，那么我们直接让ptail++即可

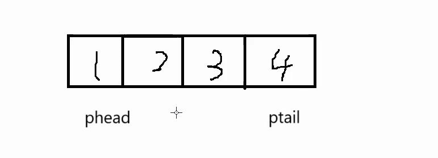
     最后经过分析我们发现底层使用数组代价更小

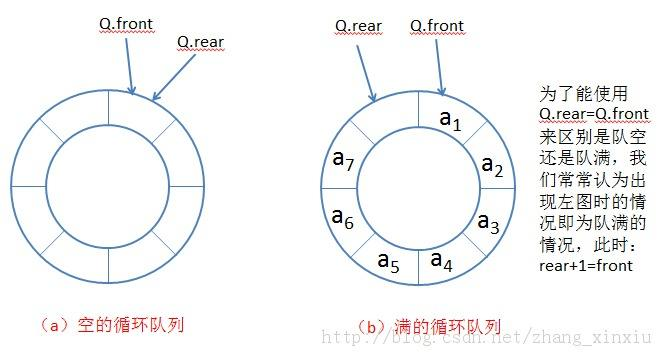
     思路 : 1 .循环队列为空：front==rear(rear是队尾，front是队头)

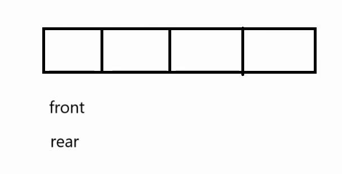
     思考：我们发现队列满的时候，rear在4数据位置，如果（rear+1）%capacity会走到front也就是a[0]位置，front=rear，这与队列为空条件一样无法区分队列为空还是满

     我们这里根据题目给的要求的capacity个空间的基础上多申请一个空间（capacity+1个空间），如下图假设题目要我们申请四个空间，我们申请五个空间，如果（rear+1)%(capacity+1) == front，那么空间就满了（思想就是始终要保留一个空位）

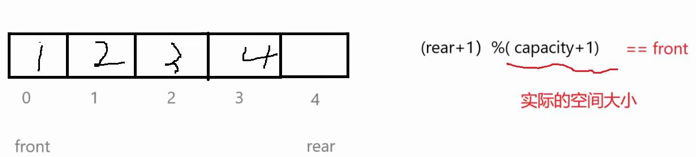
     再举个例子，如下图，rear+1=1,1%5=1，正好是front，满足队列满的时候条件，所以满了

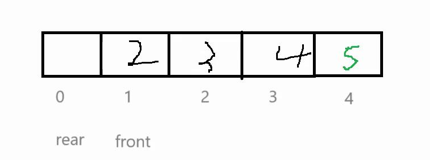
2. 循环队列满了：（rear+1)%(capacity+1) == front,（还可以定义一个size，如果size==capacity，则满，有多种方法）

代码实现：

//怎么判断循环队列是静态的还是动态的？
//静态：是否有限制规定循环队列只能是多大的空间
//动态：若循环队列的空间大小是给定的变量k，只能根据k向操作系统malloc
typedef struct {int *arr;int front;//队头int rear;//队尾int capacity;//循环队列的空间大小
} MyCircularQueue;//循环队列的初始化
MyCircularQueue* myCircularQueueCreate(int k) {MyCircularQueue*pq=(MyCircularQueue*)malloc(sizeof(MyCircularQueue));//申请k+1个空间pq->arr=(int*)malloc(sizeof(int)*(k+1));pq->front=pq->rear=0;pq->capacity=k;return pq;
}bool myCircularQueueIsEmpty(MyCircularQueue* obj) {return  obj->front==obj->rear;
}bool myCircularQueueIsFull(MyCircularQueue* obj) {return (obj->rear+1)%(obj->capacity+1)==obj->front;
}
//向循环队列插入一个元素
bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) {if(myCircularQueueIsFull(obj)){return false;}obj->arr[obj->rear++]=value;obj->rear%=obj->capacity+1;return true;}//出队列
bool myCircularQueueDeQueue(MyCircularQueue* obj) {if(myCircularQueueIsEmpty(obj)){return false;}//队列不为空obj->front++;obj->front%=obj->capacity+1;return true;
}//取队头
int myCircularQueueFront(MyCircularQueue* obj) {if(myCircularQueueIsEmpty(obj)){return -1;}return obj->arr[obj->front];
}//取队尾
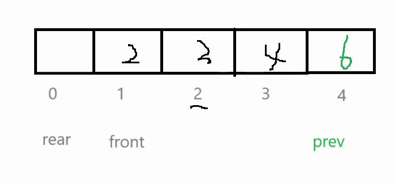
int myCircularQueueRear(MyCircularQueue* obj) {if(myCircularQueueIsEmpty(obj)){return -1;}//这里找队尾要特殊处理，可能rear是在arr[0]的位置，找不到队尾元素，会越界int prev=obj->rear-1;if(obj->rear==0){prev=obj->capacity;  }return obj->arr[prev];
}void myCircularQueueFree(MyCircularQueue* obj) {if(obj->arr)free(obj->arr);free(obj);obj=NULL;}/*** Your MyCircularQueue struct will be instantiated and called as such:* MyCircularQueue* obj = myCircularQueueCreate(k);* bool param_1 = myCircularQueueEnQueue(obj, value);* bool param_2 = myCircularQueueDeQueue(obj);* int param_3 = myCircularQueueFront(obj);* int param_4 = myCircularQueueRear(obj);* bool param_5 = myCircularQueueIsEmpty(obj);* bool param_6 = myCircularQueueIsFull(obj);* myCircularQueueFree(obj);
*/

注意：如果队尾在下标为3的位置，那么再插入个数据6，队尾rear就走到了下标为0的位置，空间满了，如果取队尾，就是rear前一个位置的数据，在未插入数据6时，队尾数据是rear-1为位置的数据4。但是在现在这种情况我们发现如果直接让rear-1不行，无法找到前一个位置，那么我们就需要特殊处理，如果rear指向a[0]处，那么队尾就在a[capacity]处
—

七、栈和队列接口实现源码

1. 栈的源码

最详细源码–点我即可直达源码

2. 队列的源码

最详细源码–点我即可直达源码

总结

     栈和队列作为基础数据结构，其 “受限操作” 特性使其在算法设计中应用广泛。掌握它们是理解更复杂数据结构（如递归、广度优先搜索）的基石。

     栈适合解决 “后进先出” 场景（如括号匹配），队列适合 “先进先出” 场景（如任务调度），而两者的相互转换则体现了数据结构灵活组合的思想。掌握它们的实现细节和应用场景，对提升编程能力和解决复杂问题具有重要意义。