图 —— 拓扑排序➕Bitset！

本文用一道例题：可达性统计介绍拓扑排序和bitset的巧妙结合，同时领略图的奥妙之处。

可达性统计

来源：

P10480 可达性统计 - 洛谷

题目大意：

给定一张 N 个点 M 条边的有向无环图，分别统计从每个点出发能够到达的点的数量。

逐步分析：

图虽然很绕，但是非常具象化，把它画出来看的话还是非常易懂的。首先我们先建立这样的一张图，让大家有个具象的概念：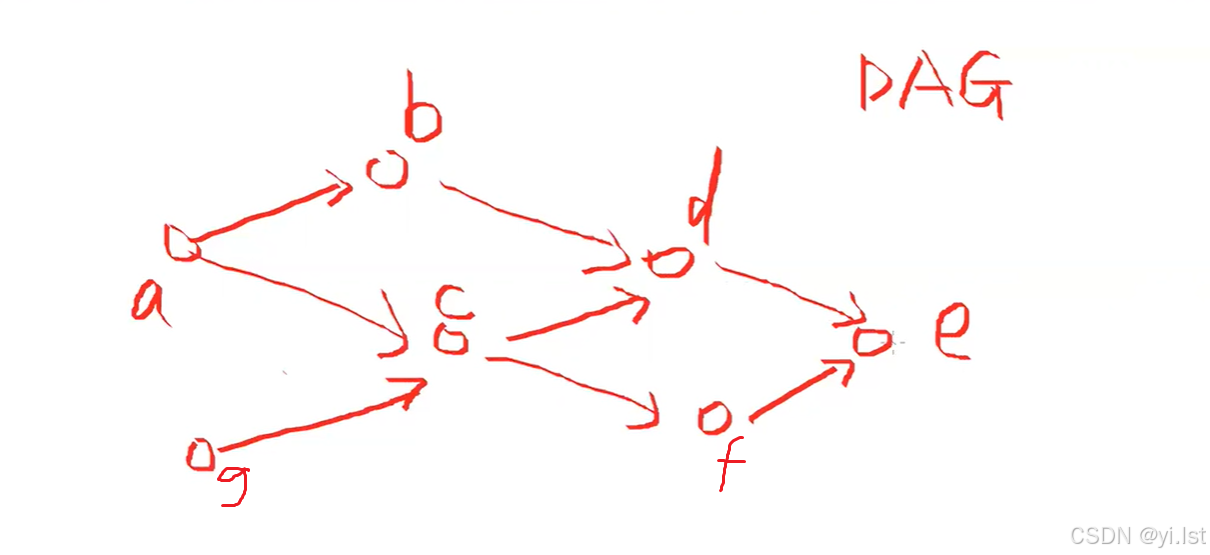

接下来参照代码一步步进行解释：

首先先介绍一下本题要用到的东西：

const int N = 30010;
int in[N];//入度：u->v那么v被u进入,入度为1。u入度为0
int topo[N];//拓扑数组
vector<int> g[N];//当前节点所能到的点。u->v,g[u]={v}
queue<int> q;//用来储存入度为0的点
int u,v;
bitset<N> dp[N];//统计dp[i]所能到的点

• in[N]：表示入度，比如图中d可以被b、c进入，那么它的入度就是2
• topo[N]：表示拓扑数组，用来存拓扑排序后点的顺序
• vector g[N]：表示当前节点能到达的点，比如c可以到达d和f，那么g[c]={d,f}
• queue q：等下要储存入度为0的节点的队列，辅助进行拓扑排序
• int u,v：分别表示一条边的起点和终点：u->v
• bitset dp[N]：每个点的可到达状态：例：dp[1]=011101,1节点可以到达第1、3、4、5节点

1、将边入图

将边存起来的同时统计它的入度。

代码：

cin >> n >> m;
for(int i=1; i<=m; i++)
{cin >> u >> v;g[u].push_back(v);//存边in[v]++;//统计入度
}

---

2、拓扑排序

根据入度进行排序，这样可以将它们的可达关系压缩成线性(数字代表本节点的入度)。

排序过程：

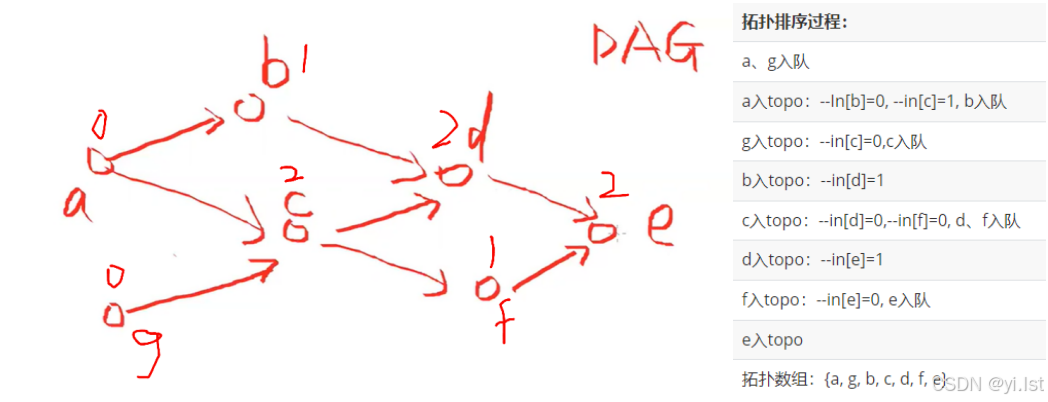
代码：

for(int i=1; i<=n; i++)//将入度为0的点放进队列
{if(in[i]==0) q.push(i);
}
int cnt=0;
while(!q.empty())
{int u=q.front();topo[cnt++]=u;//将节点放入拓扑数组for(auto v: g[u]){if(--in[v]==0)//将所连的点的入度减掉q.push(v);}q.pop();
}

---

3、统计可达性

对于排序后的数组：g[i]中的节点都能到达，而且此时g[i]中的点都已经统计过（拓扑排序的意义），我们用bitset来记录可达性，从后向前依次传递

可以看上面的那个图，应该非常易懂。

代码：

for(int i=cnt-1; i>=0; i--)
{int u=topo[i];dp[u].set(u);//先将节点本身标记上for(auto v: g[u])dp[u]|=dp[v];//将出度可达点全部赋给入度
}

---

4、输出可达点

在数每个节点的可达数量时，利用bitset的高效性可以将原先每个点O(n)的复杂度锐减至O(1)，原来总复杂度O(n²)也优化到了O(n)！

代码：

//当前节点标1(可到达)的数量
for(int i=1; i<=n; i++)cout << dp[i].count() << endl;

---

完整代码：

// Problem: P10480 可达性统计
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P10480
// Memory Limit: 512 MB
// Time Limit: 1000 ms
// 
// Powered by CP Editor (https://cpeditor.org)#include <bits/stdc++.h>
using namespace std;
#define int long long
#define pii pair<int, int>
#define fi first
#define se second 
#define endl '\n'
const int INF = 1e18;
const int N = 30010;
int in[N];//入度：u->v那么v被u进入,入度为1。u入度为0
int topo[N];//拓扑数组
vector<int> g[N];//当前节点所能到的点。u->v,g[u]={v}
queue<int> q;//用来储存入度为0的点
int u,v;
bitset<N> dp[N];//统计dp[i]所能到的点
void solve()
{cin >> n >> m;for(int i=1; i<=m; i++){cin >> u >> v;g[u].push_back(v);//存边in[v]++;//统计入度}//进行拓扑排序for(int i=1; i<=n; i++)//将入度为0的点放进队列{if(in[i]==0) q.push(i);}int cnt=0;while(!q.empty()){int u=q.front();topo[cnt++]=u;//将节点放入拓扑数组for(auto v: g[u]){if(--in[v]==0)//将所连的点的入度减掉q.push(v);}q.pop();}for(int i=cnt-1; i>=0; i--){int u=topo[i];dp[u].set(u);//先将节点本身标记上for(auto v: g[u])dp[u]|=dp[v];//将出度可达点全部赋给入度}for(int i=1; i<=n; i++)cout << dp[i].count() << endl;//当前节点标1(可到达)的数量
}
signed main()
{ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);int T=1;// cin >> T;while(T--) solve();return 0;
}
/**　　　　　　　　┏┓　　　┏┓+ +*　　　　　　　┏┛┻━━━┛┻┓ + +*　　　　　　　┃　　　　　　　┃ 　*　　　　　　　┃　　　━　　　┃ ++ + + +*　　　　　　 ████━████ ┃+*　　　　　　　┃　　　　　　　┃ +*　　　　　　　┃　　　┻　　　┃*　　　　　　　┃　　　　　　　┃ + +*　　　　　　　┗━┓　　　┏━┛*　　　　　　　　　┃　　　┃　　　　　　　　　　　*　　　　　　　　　┃　　　┃ + + + +*　　　　　　　　　┃　　　┃　Code is far away from bug with the animal protecting　　　　　　　*　　　　　　　　　┃　　　┃ + 神兽保佑,永无bug　　*　　　　　　　　　┃　　　┃*　　　　　　　　　┃　　　┃　　+　　　　　　　　　*　　　　　　　　　┃　 　　┗━━━┓ + +*　　　　　　　　　┃ 　　　　　　　┣┓*　　　　　　　　　┃ 　　　　　　　┏┛*　　　　　　　　　┗┓┓┏━┳┓┏┛ + + + +*　　　　　　　　　　┃┫┫　┃┫┫*　　　　　　　　　　┗┻┛　┗┻┛+ + + +*/

好了，本篇的内容就到这了。这个图实在是太有意思了，特出此篇博客进行讲解！本篇是煮啵自认为讲的最好的一次 ^ _ ^