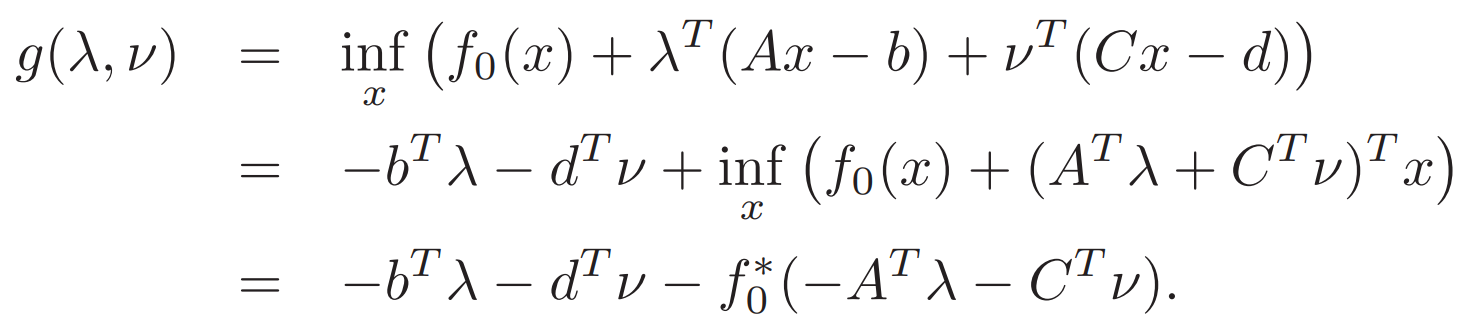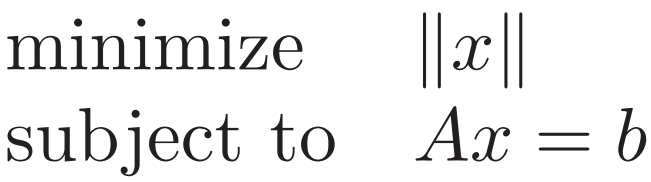NJU 凸优化导论(8) Lagrange Dual 拉格朗日对偶
目录
The Lagrange dual function 拉格朗日对偶函数（L的下界）
一、Examples
1. Least-squares solution of linear equations 线性等式 最小平方
2. Standard form LP
3. Two-way partitioning problem 二元划分 x为 1 / -1
二、Conjugate functions 共轭函数
1. Equality constrained norm minimization 等式约束的范数最小
2. Entropy Maximization 熵的最大化
3. Minimum volume covering ellipsoid 最小体积覆盖椭球
三、Making dual constraints explicit 明确对偶约束
四、Strong Duality and Slater’s Constraint Qualification强对偶以及斯拉特条件
1. QCQP 二次函数二次约束问题
2. Nonconvex Quadratic Problem 非凸二次问题
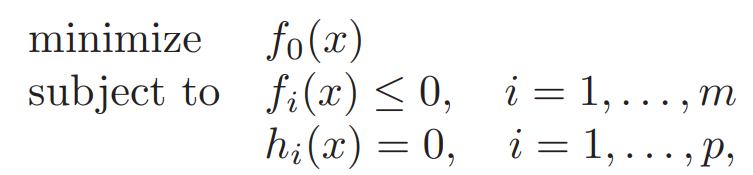不假设f0凸，有最优值p*
The Lagrange dual function 拉格朗日对偶函数（L的下界）
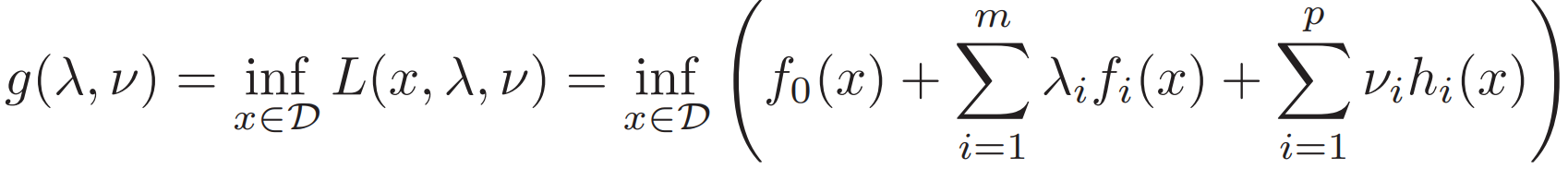
后面约束≤0 所以拉格朗日对偶函数的最小值 ≤ 原问题最小值。所以可得一个p*的下界。
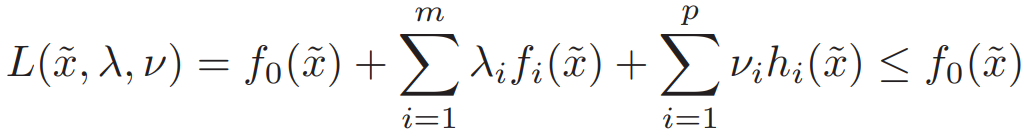
像这样，每个λ都对应一个＜p*的对偶最小值
这个关于λ的函数 g(λ)是一个凹函数
用指示函数改写 在正确范围 指示函数 I 就是 0 范围不在定义域就 ∞
我们上面的拉格朗日对偶 在f和h前加上系数 表示我们更喜欢比较小的f 对>0的f 接受但惩罚
一、Examples
1. Least-squares solution of linear equations 线性等式 最小平方
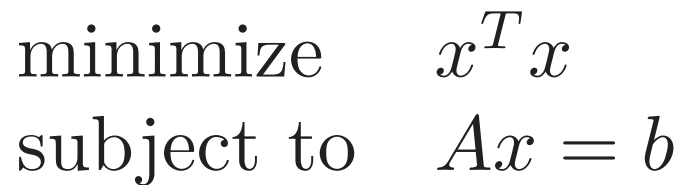
g都 ≤ 原问题下界
2. Standard form LP
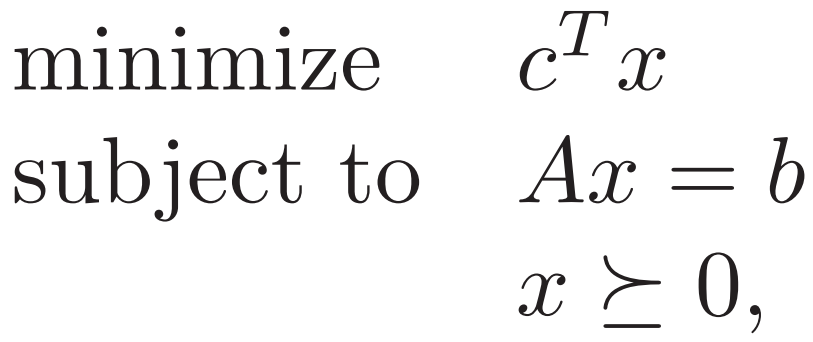不等式约束就是 
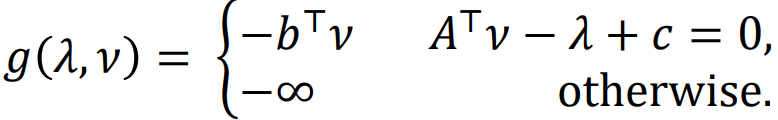若x前系数不为0 就可以到负无穷
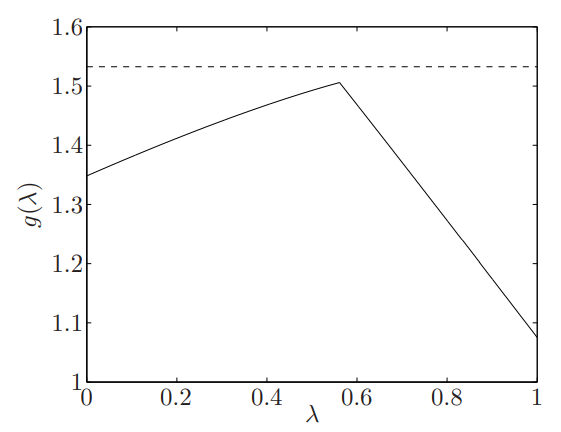
3. Two-way partitioning problem 二元划分 x为 1 / -1
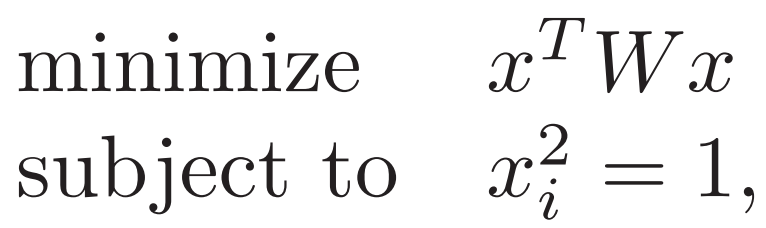
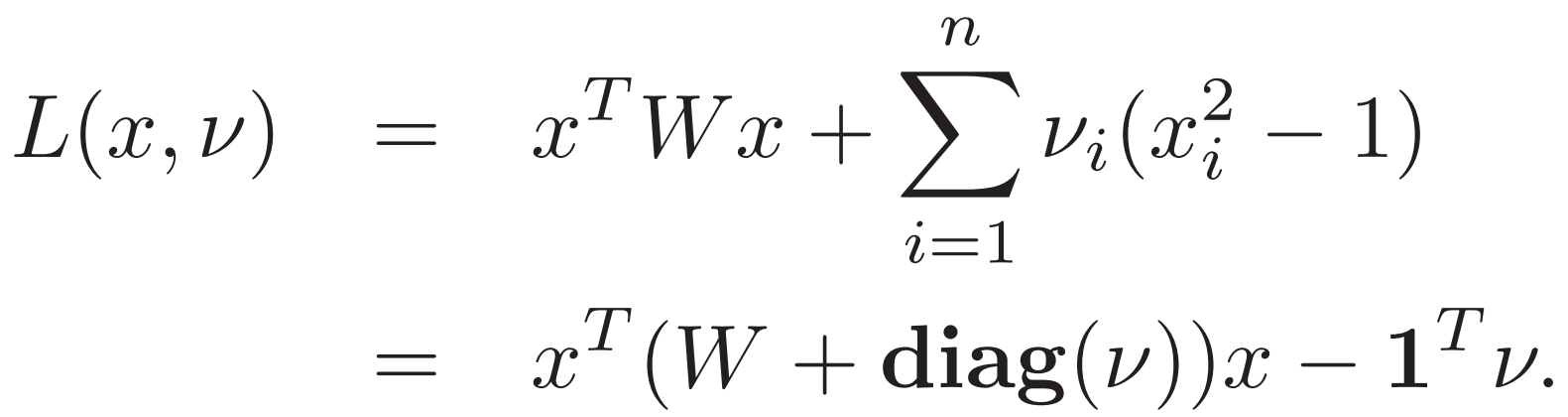
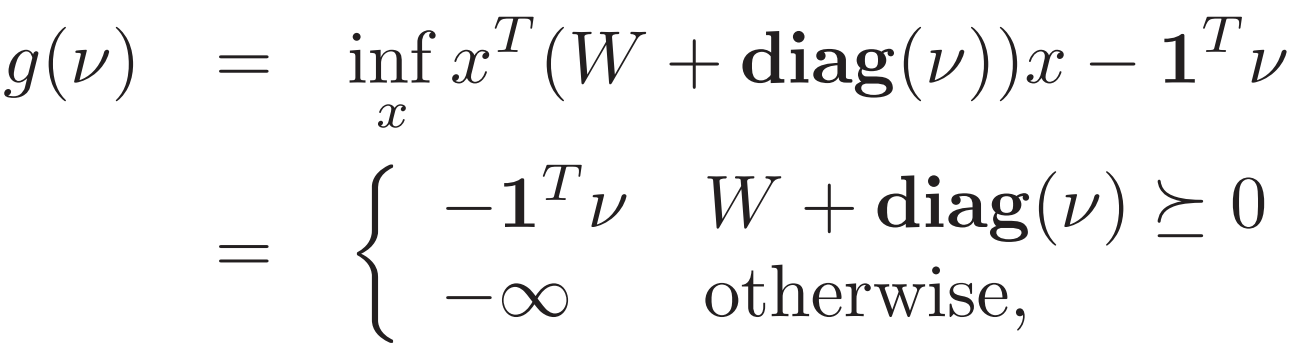每选一个v 都能得到一个下界
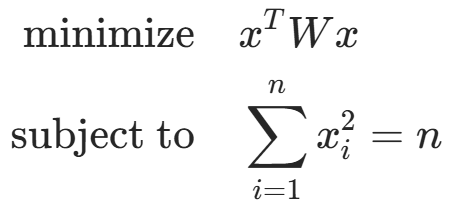（还有一种把范围放大的松弛方式 每个为1 松弛为和为n）
二、Conjugate functions 共轭函数
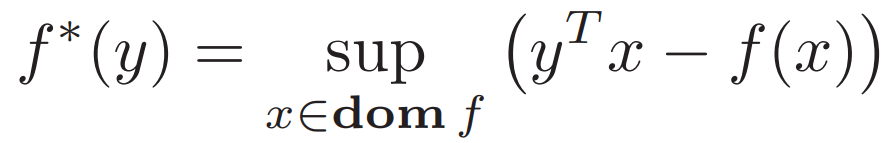
在凸函数那里讲到过共轭函数 可对应我之前的博客复习一下
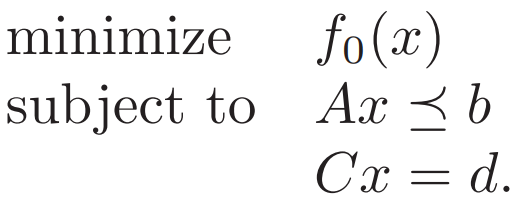
这种 不等式&等式 约束的共轭；后面求共轭的example 把矩阵对应带入即可
λ v二元 与 f0 最大距离
1. Equality constrained norm minimization 等式约束的范数最小
也可写作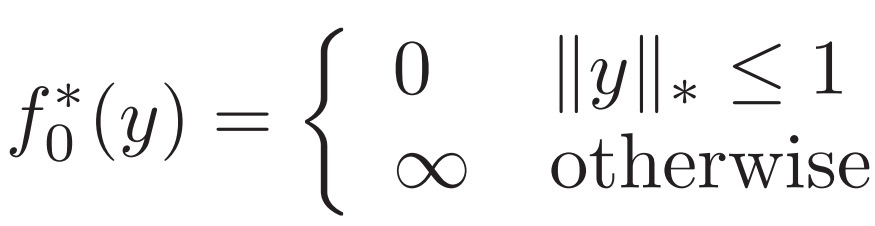 
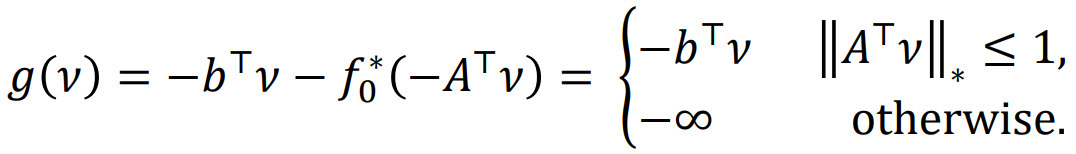
2. Entropy Maximization 熵的最大化
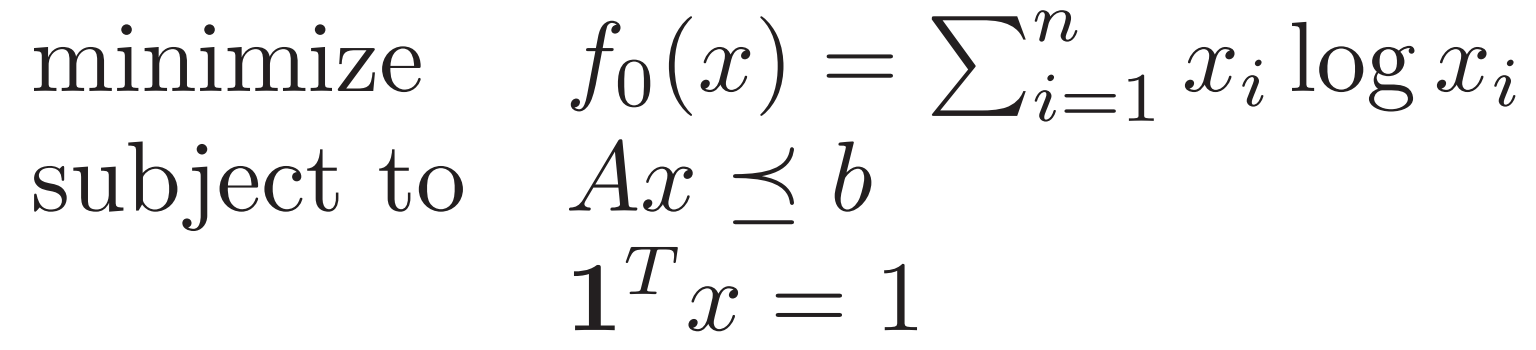
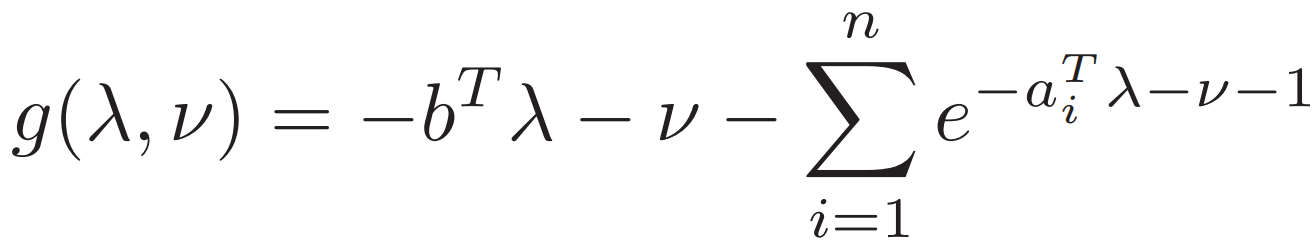
3. Minimum volume covering ellipsoid 最小体积覆盖椭球
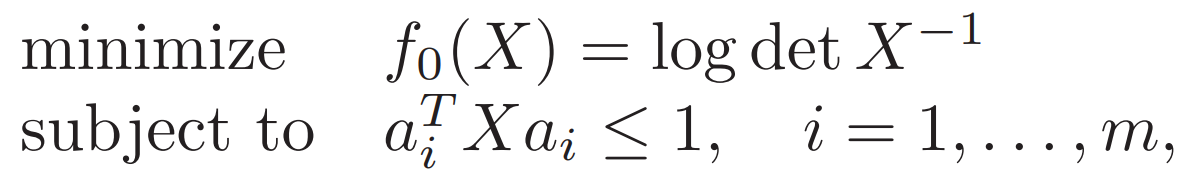
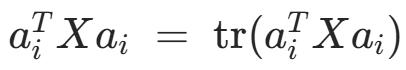
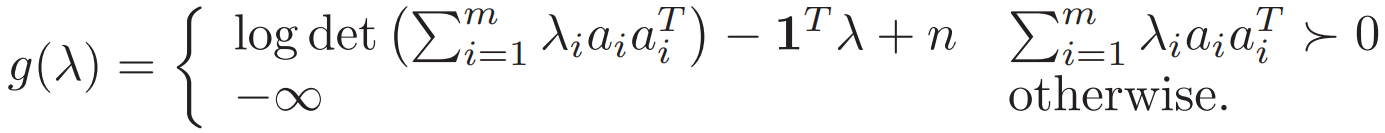
三、Making dual constraints explicit 明确对偶约束
每个λ都可对应到一个 对偶下界 我们要最紧的那个对偶下界 即为g的最大值
2. Standard form LP 上面的标准LP可把对偶约束 如下变换
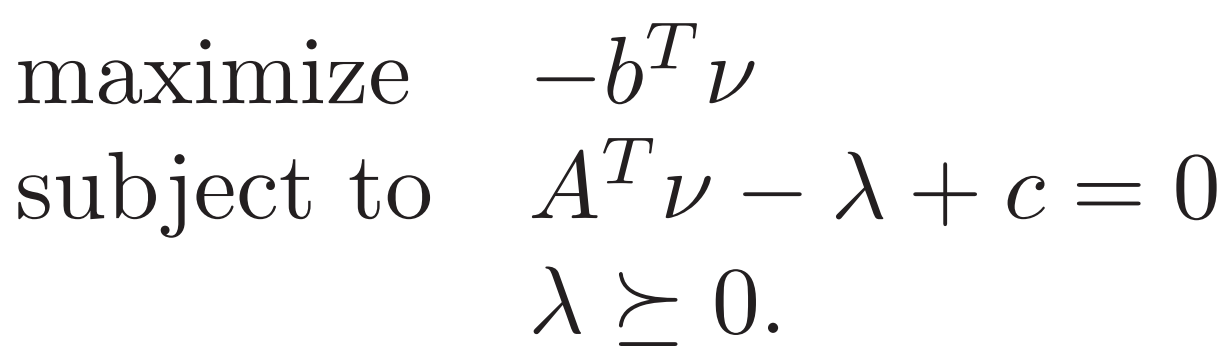
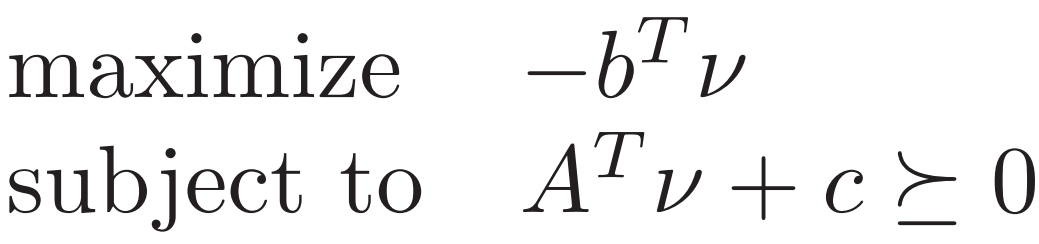
再看一个只有不等式约束的例子
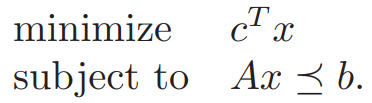
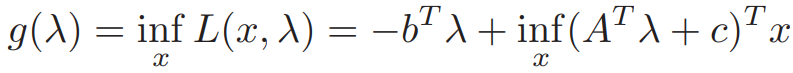
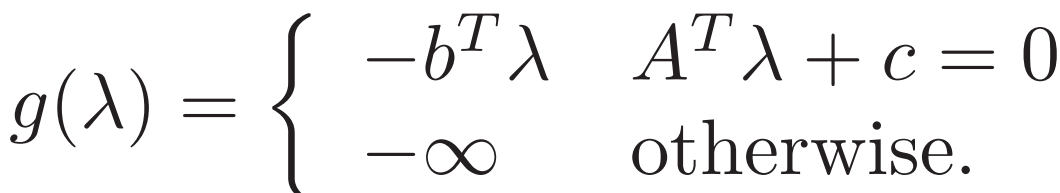
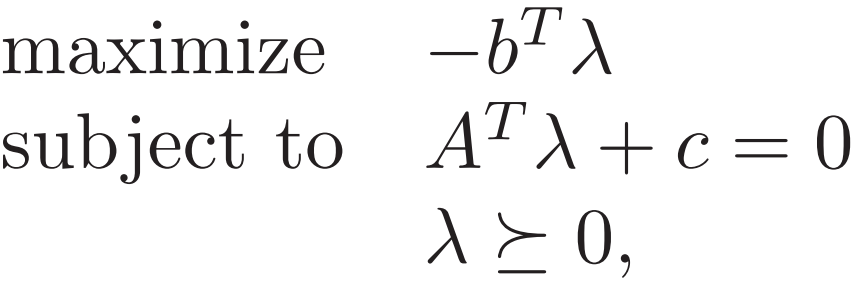
Weak duality 弱对偶性
对偶问题最大值 ≤ 原问题最小值 
四、Strong Duality and Slater’s Constraint Qualification强对偶以及斯拉特条件
对偶最优=原问题最优 
相当于可以拿对偶问题求解原问题
一种强对偶的充分条件
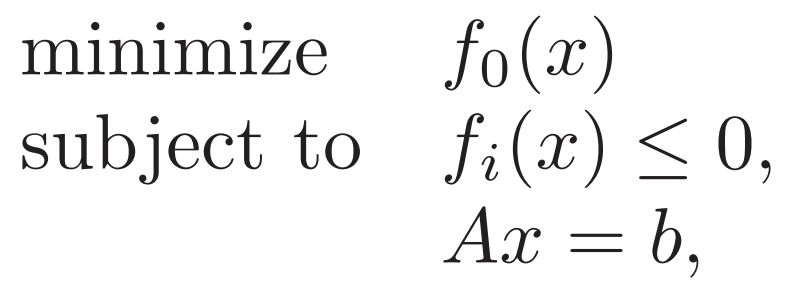
对于凸规划 如果能找到 D的相对内部点x 使得这些约束可以都严格成立 
还有个弱化版：仿射不等式约束 可不严格成立 并且f0定义域为开集
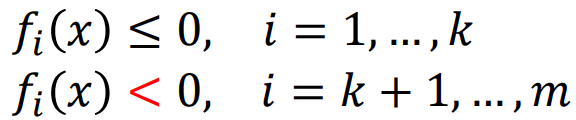
1. Least-squares solution of linear equations 线性等式 最小平方
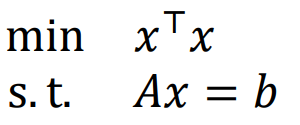这个问题无不等式约束 可以找到内部点 x=0 故是强对偶的
同理对于 Standard form LP 只要原问题或者对偶问题存在可行点 就是强对偶的
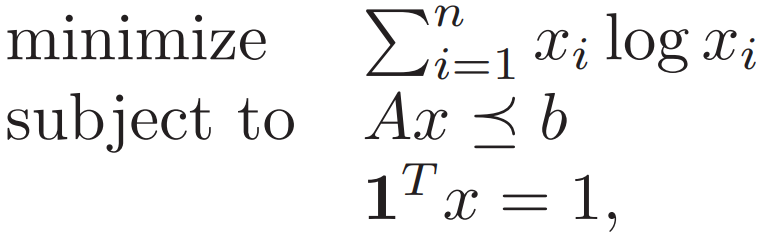原问题和对偶问题分别为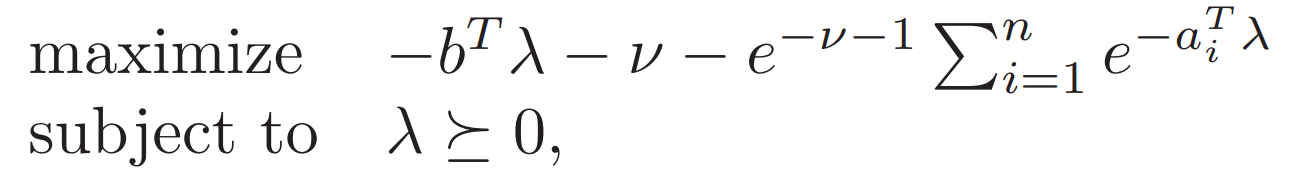
如果存在相对内部点x 满足
即为强对偶
对偶问题对v求导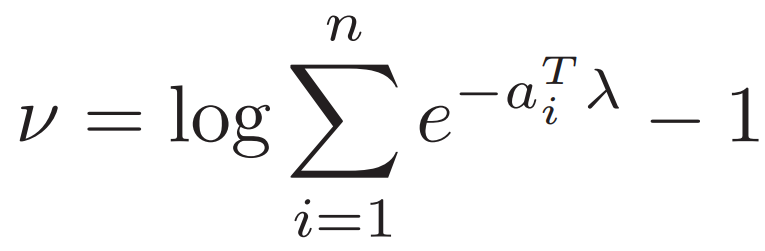 
代入得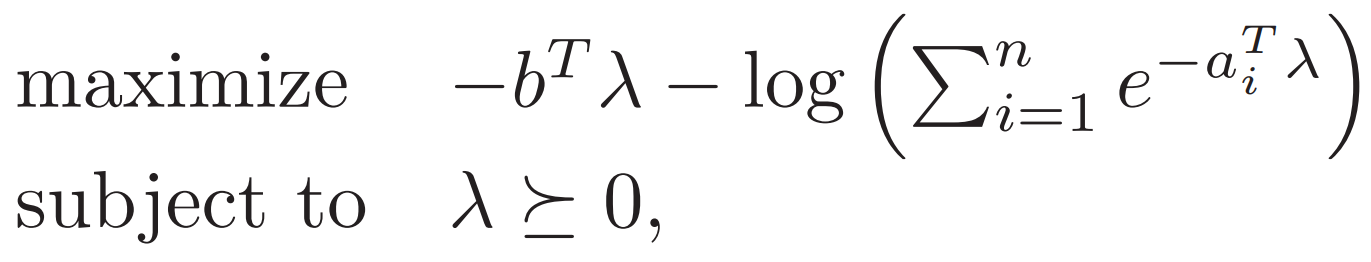
3. Minimum volume covering ellipsoid 最小体积覆盖椭球
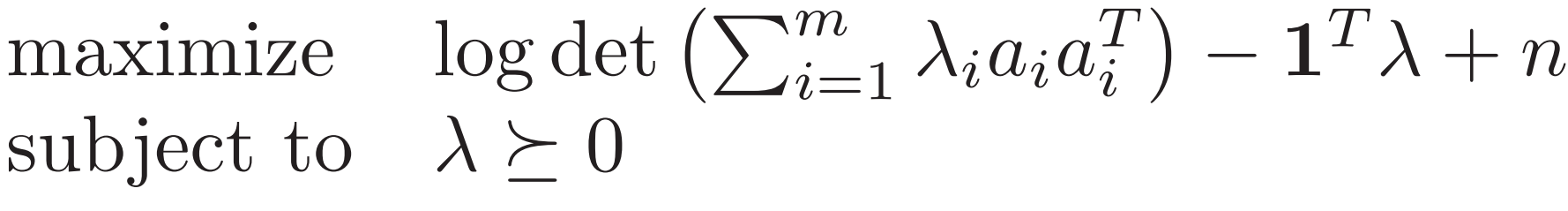
若存在相对内部点x 满足 
即为强对偶
1. QCQP 二次函数二次约束问题
2. Nonconvex Quadratic Problem 非凸二次问题
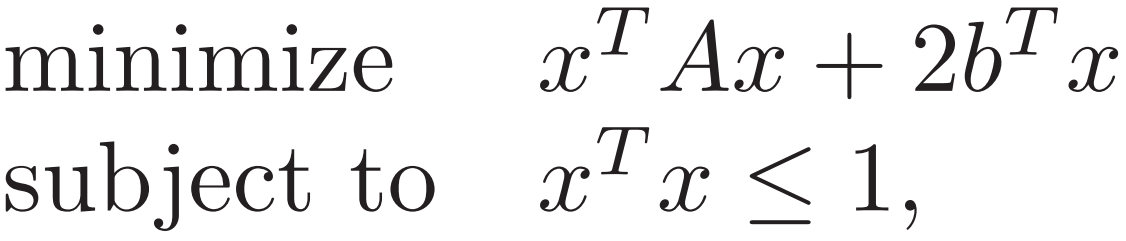
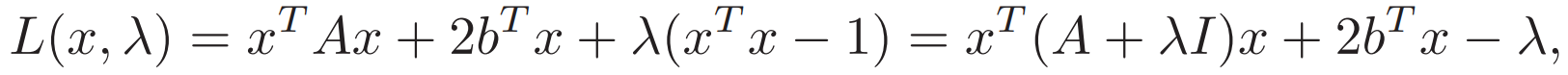
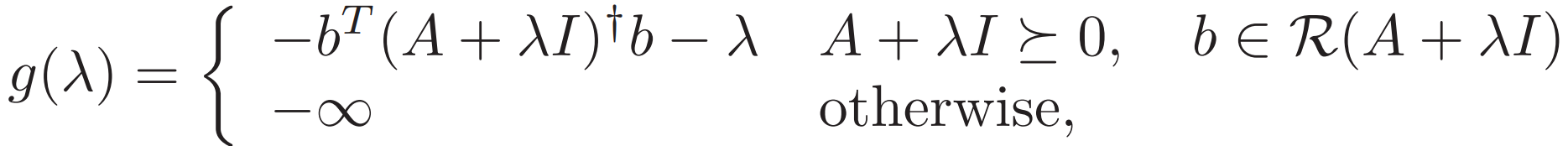
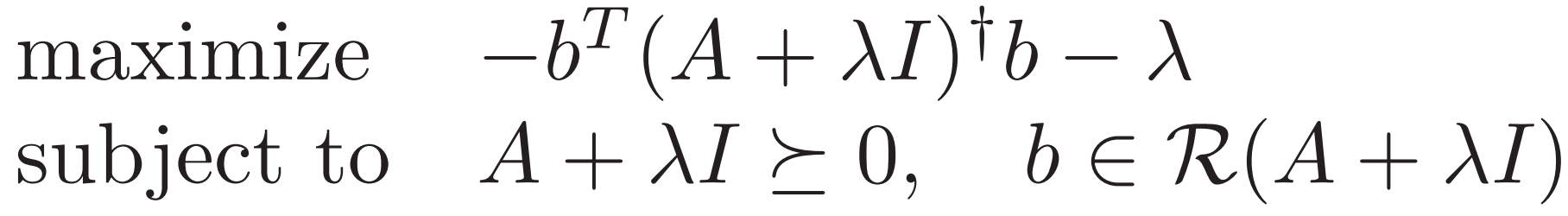
由半正定 最小特征值 ≥0
转化为特征值λ 特征向量q 可把对偶问题写作
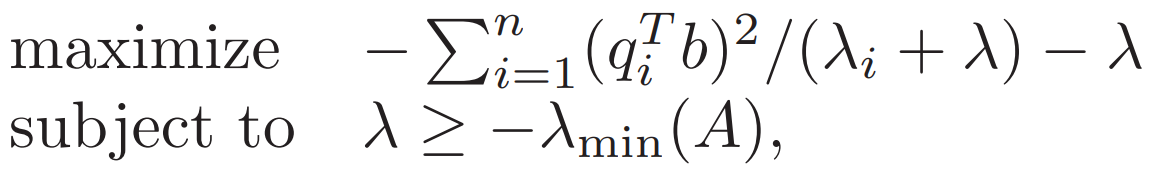
进而推广到更一般的结论：对于任何具有二次目标函数和一个二次不等式约束的优化问题
只要斯莱特条件（Slater’s condition ）成立，就有强对偶性