JS - - - - - 数组乱序排序「进阶版」

1. 使用.sort()进行乱序排序

1.1 简单示例

function sortShuffle(arr) {return arr.sort(()=> Math.random() - 0.5);
}function start() {for(let i = 0; i < 10; i++){let arr = ['a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i', 'j'];sortShuffle(arr);console.log('arr', arr)}
}start()

打印的结果看似真的已经随机了，但是事实真的如此吗？

由于基数小，得到的数据不一定准确。接下来增加次数，以验证随机性的真实性。

1.2 加大基数

代码如下：

function sortShuffle(arr) {return arr.sort(()=> Math.random() - 0.5);
}function start() {// 循环10w次let num = 100000;// 统计元素在每个位置出现的次数let elementPositionCounts = {a: Array.from({length:10}).fill(0),b: Array.from({length:10}).fill(0),c: Array.from({length:10}).fill(0),d: Array.from({length:10}).fill(0),e: Array.from({length:10}).fill(0),f: Array.from({length:10}).fill(0),g: Array.from({length:10}).fill(0),h: Array.from({length:10}).fill(0),i: Array.from({length:10}).fill(0),j: Array.from({length:10}).fill(0)}for(let i = 0; i < num;  i++){let arr = ['a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i', 'j'];sortShuffle(arr);elementPositionCounts.a[arr.indexOf('a')]++;elementPositionCounts.b[arr.indexOf('b')]++;elementPositionCounts.c[arr.indexOf('c')]++;elementPositionCounts.d[arr.indexOf('d')]++;elementPositionCounts.e[arr.indexOf('e')]++;elementPositionCounts.f[arr.indexOf('f')]++;elementPositionCounts.g[arr.indexOf('g')]++;elementPositionCounts.h[arr.indexOf('h')]++;elementPositionCounts.i[arr.indexOf('i')]++;elementPositionCounts.j[arr.indexOf('j')]++;}// 以表格形式，展示结果console.table(elementPositionCounts);
}start()

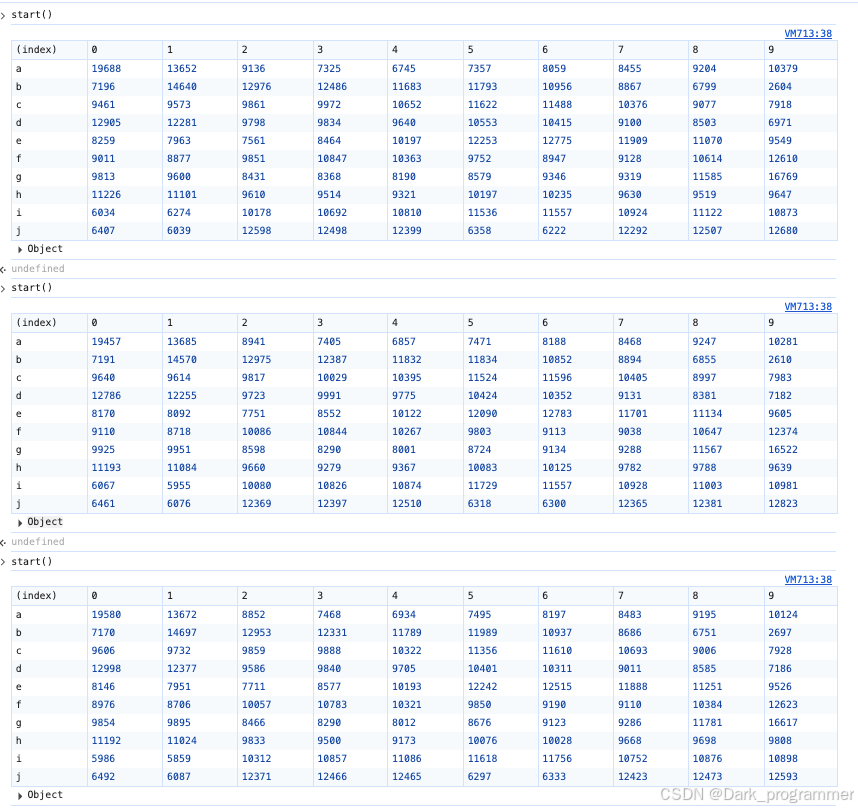
从表格中可以明显看出，各元素在不同位置的出现概率存在显著差异。

各列数据统计了不同元素在相同位置的出现频率
以第一列为例：
最高频元素"a"出现约19.5k次
而最低频元素"i"仅出现约6k次。

2. 使用「洗牌算法 Fisher-Yates 」进行乱序排序

每次从未处理的数组中随机取一个元素，然后把该元素放到数组的尾部，即数组的尾部放的就是已经处理过的元素。
这是一种原地打乱的算法，每个元素随机概率也相等，时间复杂度从 Fisher 算法的 O(n2)提升到了 O(n)

// Fisher-Yates 洗牌算法
function shuffle(arr) {const array = [...arr]; // 创建副本，避免修改原数组for (let i = array.length - 1; i > 0; i--) {const j = Math.floor(Math.random() * (i + 1)); // 生成 [0, i] 的随机数[array[i], array[j]] = [array[j], array[i]]; // 交换元素 （解构赋值的方式交换位置）}return array;
}function start() {const num = 100000; // 循环次数const elements = ['a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i', 'j'];// 使用reduce初始化统计对象const elementPositionCounts = elements.reduce((acc, el) => {acc[el] = Array(elements.length).fill(0);return acc;}, {});// 进行洗牌并统计位置for (let i = 0; i < num; i++) {const shuffled = shuffle(elements);shuffled.forEach((el, pos) => {elementPositionCounts[el][pos]++;});}// 输出结果console.table(elementPositionCounts);
}start();

结果如下：

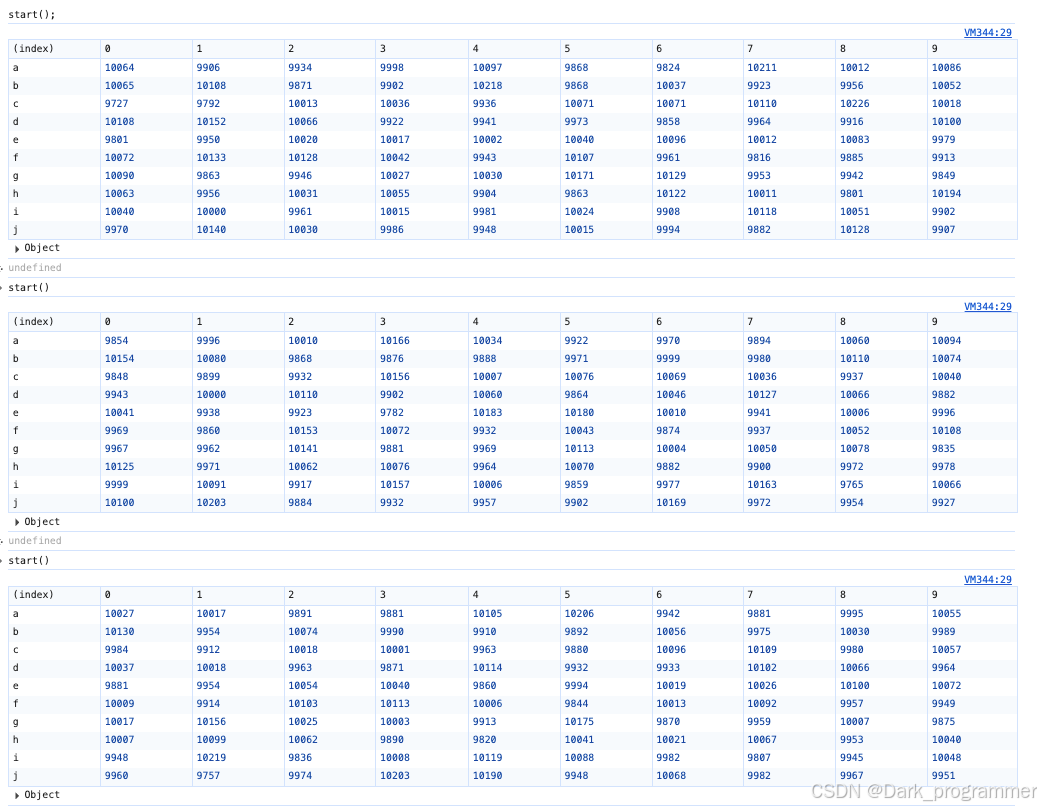
从表格中我们可以看出，每个元素在每个位置出现的次数已经相差不大。

每一列中各元素出现的次数基本已经很平均了。