永磁同步电机MTPA与MTPV曲线具体仿真实现
永磁同步电机MTPA与MTPV曲线具体仿真实现
近期做了一些标定试验,实际电机参数并不是确定的,而是变化的,因此很难通过解析的方法算出MTPA的对应点,以及在弱磁区如何过度到MTPV。这个在实际情况下都是一点点标出来的,我这里用仿真的方式进行验证
一、引言
- 永磁同步电机概述:介绍永磁同步电机(PMSM)的基本结构、工作原理及在工业中的应用,强调高效控制的重要性。
- MTPA与MTPV概念:定义最大转矩每安培(MTPA)和最大转矩每伏特(MTPV)策略,解释其在优化电机效率、减少能耗方面的作用。
- 标定需求:说明为何需要标定MTPA和MTPV曲线
二、MTPA与MTPV的理论基础
-
电机数学模型:基于d−qd-qd−q坐标系,建立PMSM的动态方程:
- 电压方程:vd=Rsid+Lddiddt−ωeLqiqv_d = R_s i_d + L_d \frac{di_d}{dt} - \omega_e L_q i_qvd=Rsid+Lddtdid−ωeLqiq
vq=Rsiq+Lqdiqdt+ωe(Ldid+λf)v_q = R_s i_q + L_q \frac{di_q}{dt} + \omega_e (L_d i_d + \lambda_f)vq=Rsiq+Lqdtdiq+ωe(Ldid+λf)
其中,vdv_dvd、vqv_qvq为d−qd-qd−q轴电压,idi_did、iqi_qiq为d−qd-qd−q轴电流,RsR_sRs为定子电阻,LdL_dLd、LqL_qLq为电感,λf\lambda_fλf为永磁体磁链,ωe\omega_eωe为电角速度。 - 转矩方程:Te=32P[λfiq+(Ld−Lq)idiq].......(1)T_e = \frac{3}{2} P \left[ \lambda_f i_q + (L_d - L_q) i_d i_q \right] .......(1)Te=23P[λfiq+(Ld−Lq)idiq].......(1)
其中,TeT_eTe为电磁转矩,PPP为极对数。
- 电压方程:vd=Rsid+Lddiddt−ωeLqiqv_d = R_s i_d + L_d \frac{di_d}{dt} - \omega_e L_q i_qvd=Rsid+Lddtdid−ωeLqiq
-
MTPA原理:最大化每安培转矩,即在给定电流IsI_sIs(Is=id2+iq2I_s = \sqrt{i_d^2 + i_q^2}Is=id2+iq2)下,求解最优idi_did和iqi_qiq使Te/IsT_e/I_sTe/Is最大。条件为:
∂Te∂id=0\frac{\partial T_e}{\partial i_d} = 0∂id∂Te=0
具体推导过程我就不复述了,网上一堆,具体就是使用拉格朗日乘数法解最值,这里直接给出结论:
−λf+λf2+4(Ld−Lq)2∗iq22(Ld−Lq)=id.......(2)\frac{-\lambda_f+\sqrt{\lambda_f^2+4(L_d-L_q)^2*i_q^2}}{2(L_d-L_q)} = i_d.......(2)2(Ld−Lq)−λf+λf2+4(Ld−Lq)2∗iq2=id.......(2)
因此对于不同的转矩Te,解出满足方程(1)和(2)的id和iq,即为MTPA的曲线,这个过程可以交给Matlab(后面会贴出代码) -
MTPV原理:最大化每伏特转矩,即在电压限制VsV_sVs(Vs=vd2+vq2V_s = \sqrt{v_d^2 + v_q^2}Vs=vd2+vq2)下,求解最优idi_did和iqi_qiq使Te/VsT_e/V_sTe/Vs最大,考虑电压饱和约束。
直接给出结论:
−λfLd+−Lqλf+Lq∗λf2+4(Ld−Lq)2∗iq22Ld(Ld−Lq)=id.......(3)\frac{-\lambda_f}{L_d}+ \frac{-L_q\lambda_f+L_q*\sqrt{\lambda_f^2+4(L_d-L_q)^2*iq^2}}{2L_d(L_d-L_q)}= i_d.......(3)Ld−λf+2Ld(Ld−Lq)−Lqλf+Lq∗λf2+4(Ld−Lq)2∗iq2=id.......(3)
四、仿真标定步骤
- 仿真平台(如MATLAB/Simulink)
| 参数 | 值 |
|---|---|
| 版本 | matlab2019a |
| 极对数 | 5 |
| Rs | 0.007 |
| Ld | 0.00009 |
| Lq | 0.00017 |
| 磁链Phif | 0.019 |
| 转动惯量J | 1e-2 |
| 死区时间 | 2微秒 |
| Udc | 48V |
| Imax | 300A |
| 控制周期 | 100微秒 |
| 开关频率 | 10kHz |
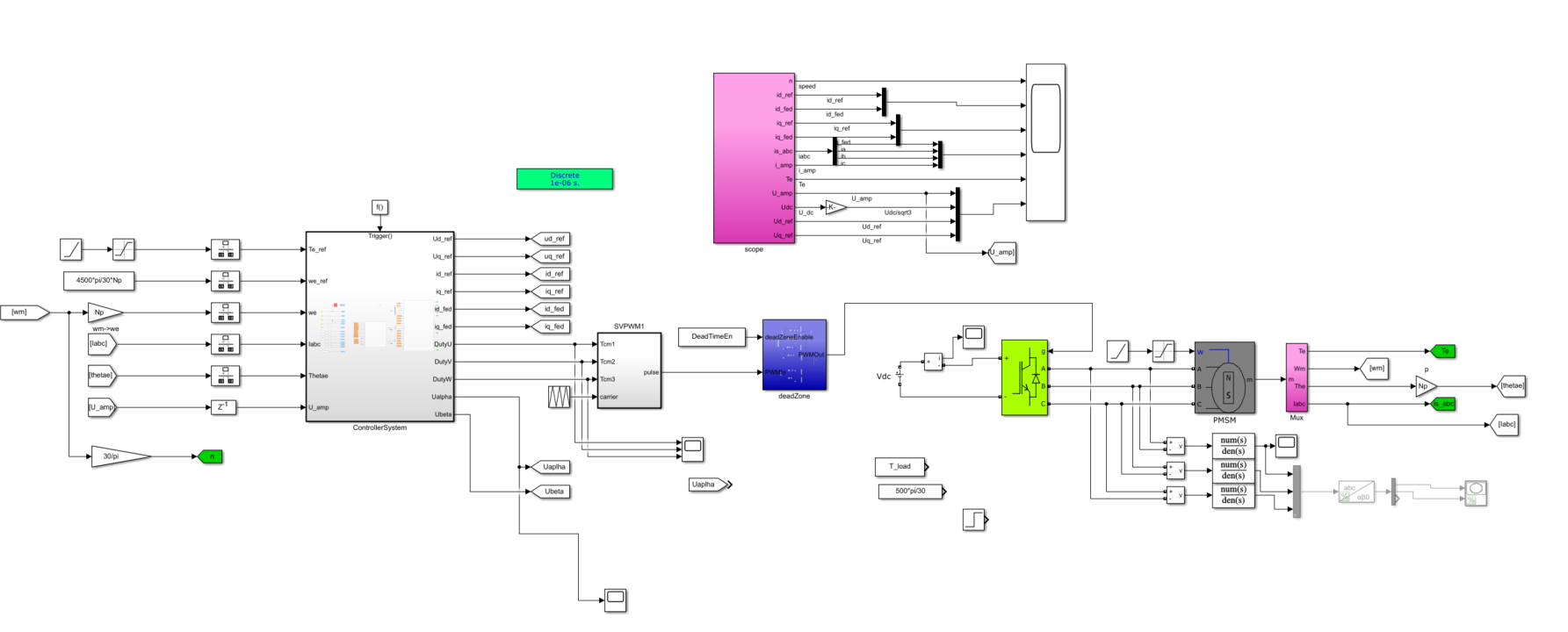
图1:仿真概览图
- 画出该电机对应的MTPA和MTPV曲线
% 基本参数输入
Ld=0.00009;
Lq=0.00017;
Rs = 0.007;
phir= 0.019;
udc=48;
ulim=udc/sqrt(3);
imax=300;
np=5;% 中间量处理
T_values = 0:5:65;
T_speed = 0:500:5000;
T_we = T_speed*pi./30*np;
range = [-400,400];
text_pos_mtpa = range(1)/2;
text_pos_mtpv = range(1);
text_pos_t = 0;
text_pos_we = range(1)/2;
% colors = hsv(length(T_values));
% 定义符号变量
syms id iq% 创建图形窗口
figure;
% 循环绘制不同T值下的曲线
for i = 1:length(T_values)T = T_values(i);% 定义方程eqn = T == 1.5*np*(phir*iq + (Ld-Lq)*iq*id);h = ezplot(eqn, range);set(h, 'Color','r'); hold on;sol_iq = solve(subs(eqn, id, text_pos_t), iq);text(text_pos_t, sol_iq, ['T = ', num2str(T)], 'HorizontalAlignment', 'center', 'VerticalAlignment', 'bottom', 'Color', 'r','FontSize', 8);
endeqn = imax^2 == id^2+iq^2;
ezplot(eqn, range);
hold on;for i = 1:length(T_we)we = T_we(i);n = T_speed(i);% 定义方程eqn = ulim^2 == (Rs*id-we*Lq*iq)^2+(Rs*iq+we*Ld*id+we*phir)^2;h = ezplot(eqn,range);set(h, 'Color', 'g'); hold on;sol_iq = solve(subs(eqn, id, text_pos_we), iq);text(text_pos_we, sol_iq(2), ['n= ', num2str(n)], 'HorizontalAlignment', 'center', 'VerticalAlignment', 'bottom', 'Color', 'g','FontSize', 8);
end
% 画MTPA曲线
eqn = id == (-phir+sqrt(phir^2+4*(Ld-Lq)^2*iq^2))/(2*(Ld-Lq));
h = ezplot(eqn,range);
set(h, 'Color', 'b');
hold on;
sol_iq = solve(subs(eqn, id, text_pos_mtpa), iq);
text(text_pos_mtpa, sol_iq(2), 'MTPA', 'HorizontalAlignment', 'center', 'VerticalAlignment', 'bottom', 'Color', 'b','FontSize', 8);% 画MTPV曲线
eqn = id == -phir/Ld+(-Lq*phir+Lq*sqrt(phir^2+4*(Ld-Lq)^2*iq*iq))/(2*Ld*(Ld-Lq));
h = ezplot(eqn,range);
set(h, 'Color', 'm');
hold on;
sol_iq = solve(subs(eqn, id, text_pos_mtpv), iq);
text(text_pos_mtpv, sol_iq(2), 'MTPV', 'HorizontalAlignment', 'center', 'VerticalAlignment', 'bottom', 'Color', 'm','FontSize', 8);% 画点
plot(0, 0, 'ko', 'MarkerFaceColor', 'k');
plot(-phir/Ld, 0, 'ko', 'MarkerFaceColor', 'r');% 添加标题和坐标轴标签
title('Plot of MTPA');
xlabel('id');
ylabel('iq');
% 获取当前坐标轴对象
% 绘制 id = 0 的黑色竖线
xline(0, 'k', 'LineWidth', 1);
% 绘制 iq = 0 的黑色横线
yline(0, 'k', 'LineWidth', 1);
ax = gca;
% 设置坐标轴颜色为黑色
ax.XColor = 'k';
ax.YColor = 'k';
% 设置坐标轴线条宽度
ax.LineWidth = 1;
% 显示网格线
grid on;
hold off; 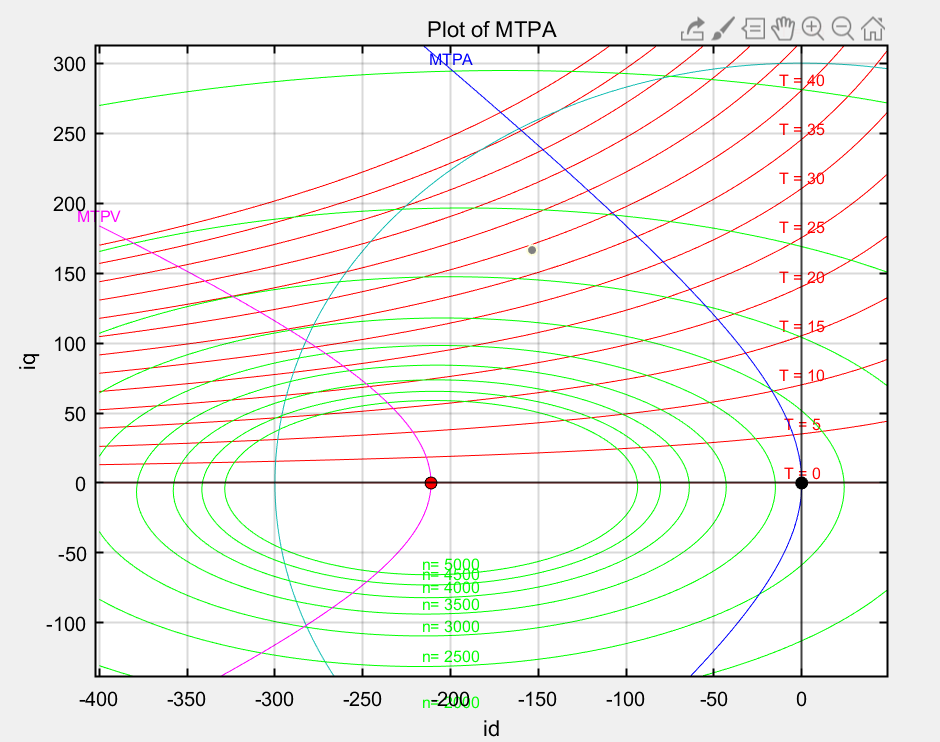
图2:MTPA&MTPV曲线
-
电机用台架模式控制,即转速是直接给定,控转矩,电流环用内模控制
关于内模控制可以看我往期文章
首先解析根据绘出的曲线可以得到需求扭矩Te和需求电流Id的关系,仿真中可以用查表法
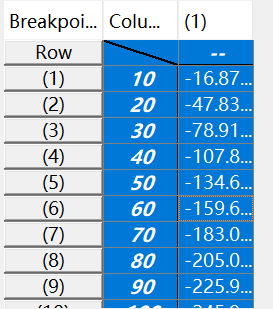
图3:Te和id的查表关系
已知Te和需求Id了,计算Iq就是手到擒来了,根据转矩公式(1)可以算出需求的iq -
电机给固定转速1000rpm,在基速区得到最大转矩对应的电流坐标
给定请求转矩65Nm
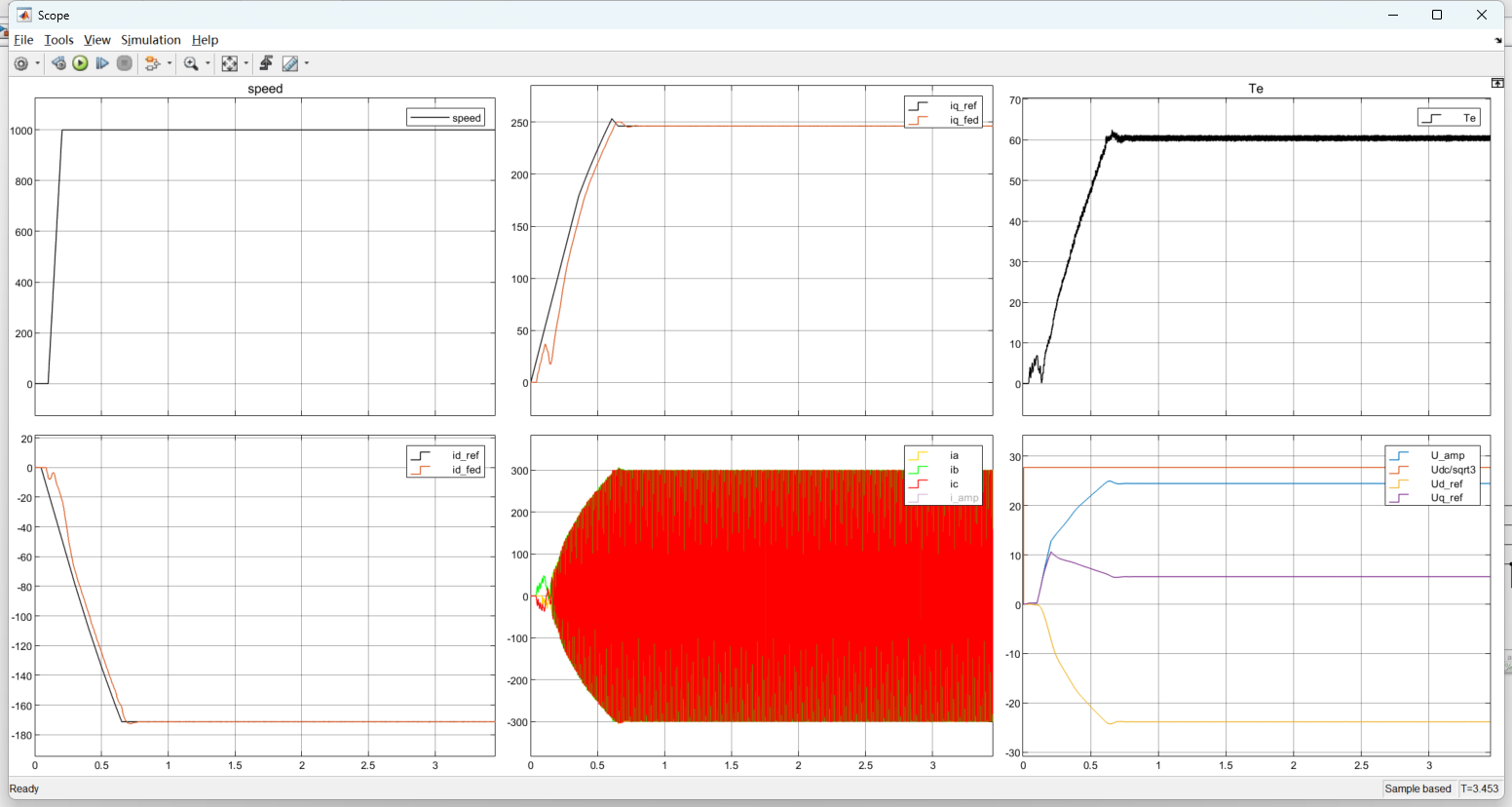
图4:1000Rpm&TqRequest65Nm
在基速区,给定1000rpm和请求65Nm时候,此时起主要限制的是电流环,由于电流环的限制,iq电流不能继续增大,因而被限制在了246A,电流id给定是-171,A,你可以将该点描绘在MTPA那个图中
plot(-171, 246, 'ko', 'MarkerFaceColor', 'g');
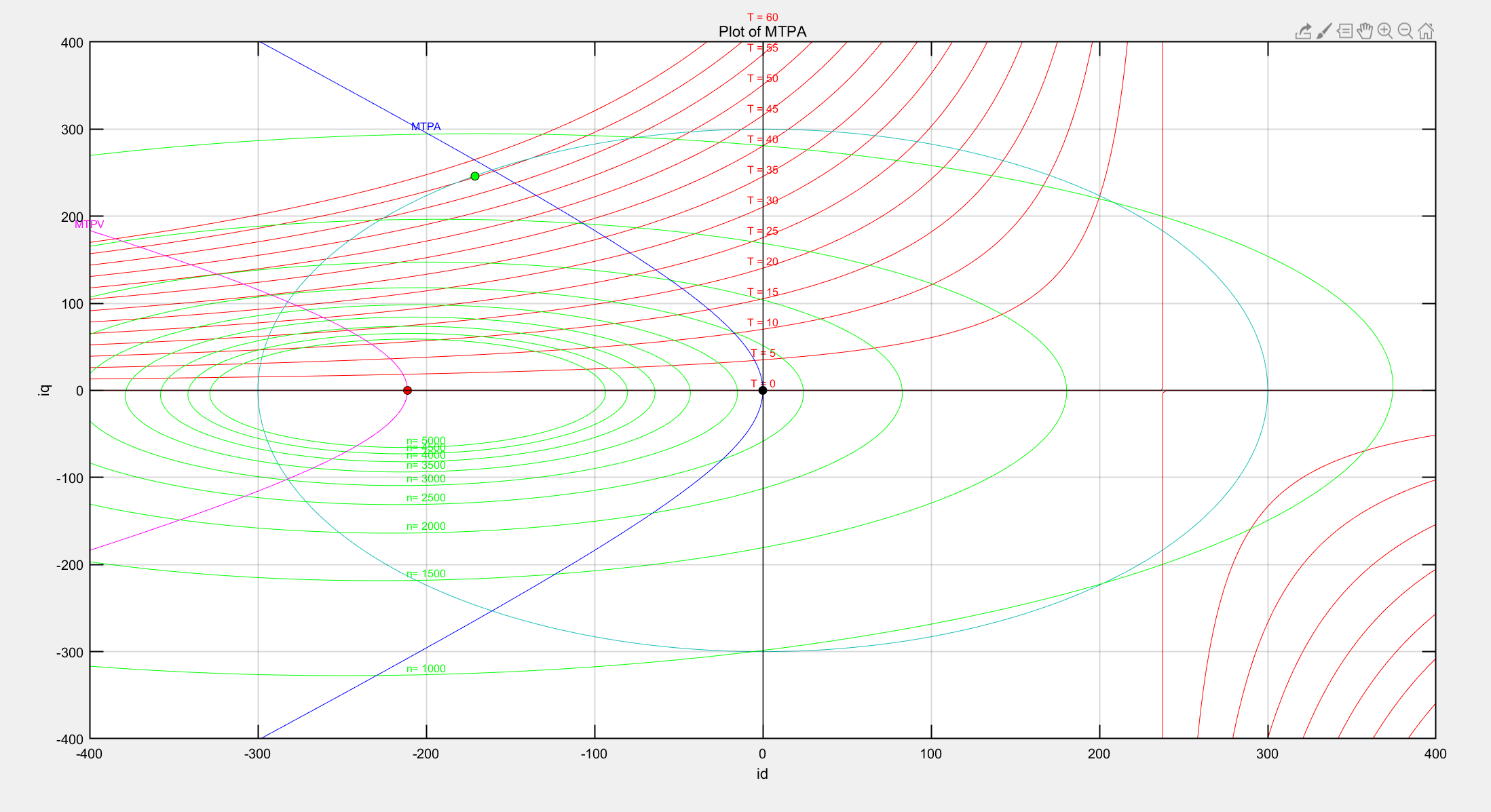
图5:MTPA最大转矩点
如上图的绿色点,恰好在电流圆上,且也和Te=60Nm的曲线相切,此时电机输出最大扭矩。如果我们请求扭矩是60Nm,则该点就能正好落在MTPA曲线上了,这里我们故意请求一个更大的扭矩,由于65Nm对应的id会偏左,因此解出来的点也就脱离MTPA了,但是依然可以输出最大扭矩,只是该工作点并不是效率最高的点。
- 进一步增大转速,如何保证弱磁过程中的id沿着我们期望的那条电流圆外包络线移动到MTPV曲线?
对于一个明确参数的仿真系统,我们当然可以用解析的方法,算出曲线上的每个点,然后用转速、需求转矩查表的方法,把id,iq全都通过查表查出来,但是这个在实际系统上是很难做到的,这里我们用仿真演示一下实际系统中,如何通过试验标定的方法得到id,使得系统的id,iq一直沿着我们想要的曲线移动
我们把转速升到1500rpm,请求转矩依然是65Nm
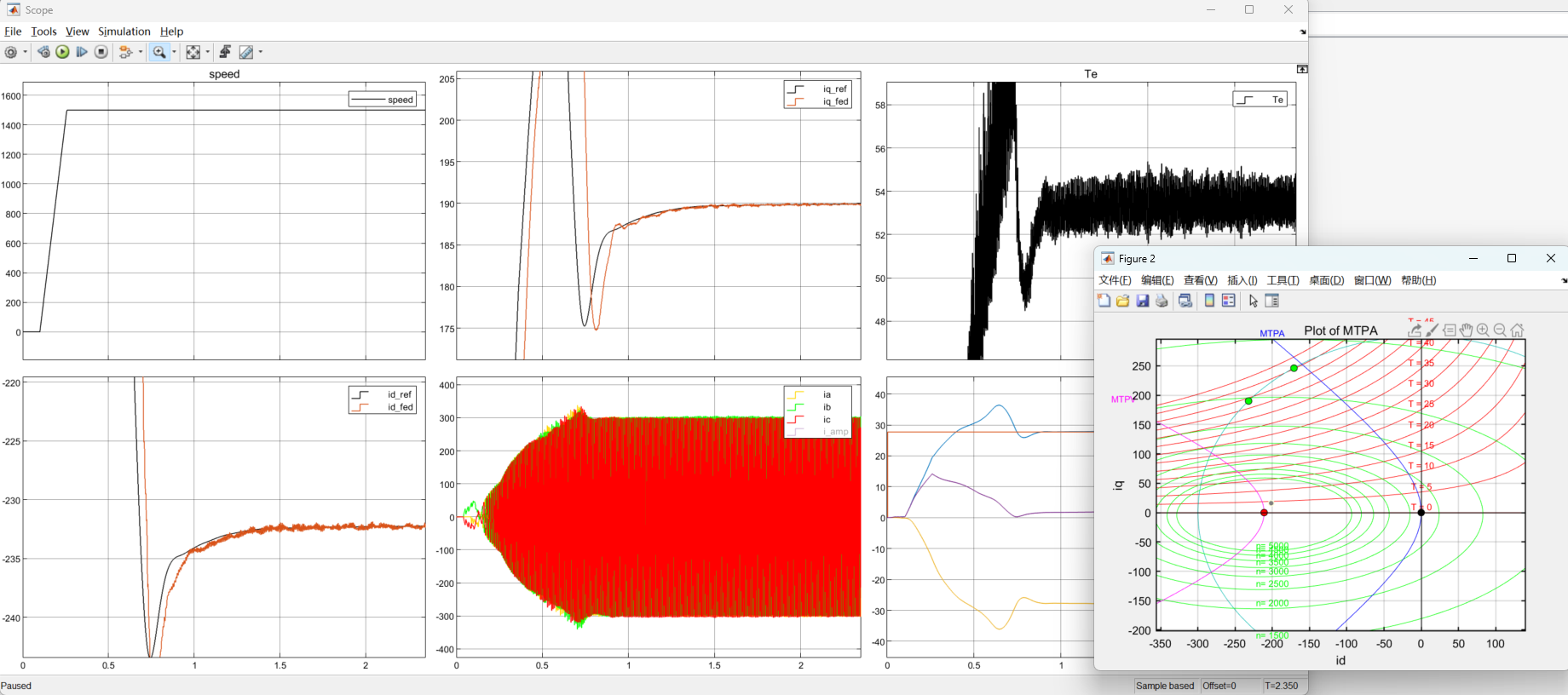
图6:1500Rpm&65Nm
此时进入弱磁区,id由于弱磁环的作用慢慢移动到-232,iq也由于电流环的限制到了90A,此时出的转矩是53.5Nm
同样,我们画出这个点
可以看到这个点似乎是沿着电流圆走的,似乎我们并不需要做其他的限制,系统在弱磁环的作用下自动将电流工作点限制在电流环和电压环内了。但实际上,这个点并不是最优点,但是也已经很接近了,倘若我们把id电流限制在-224,再次仿真
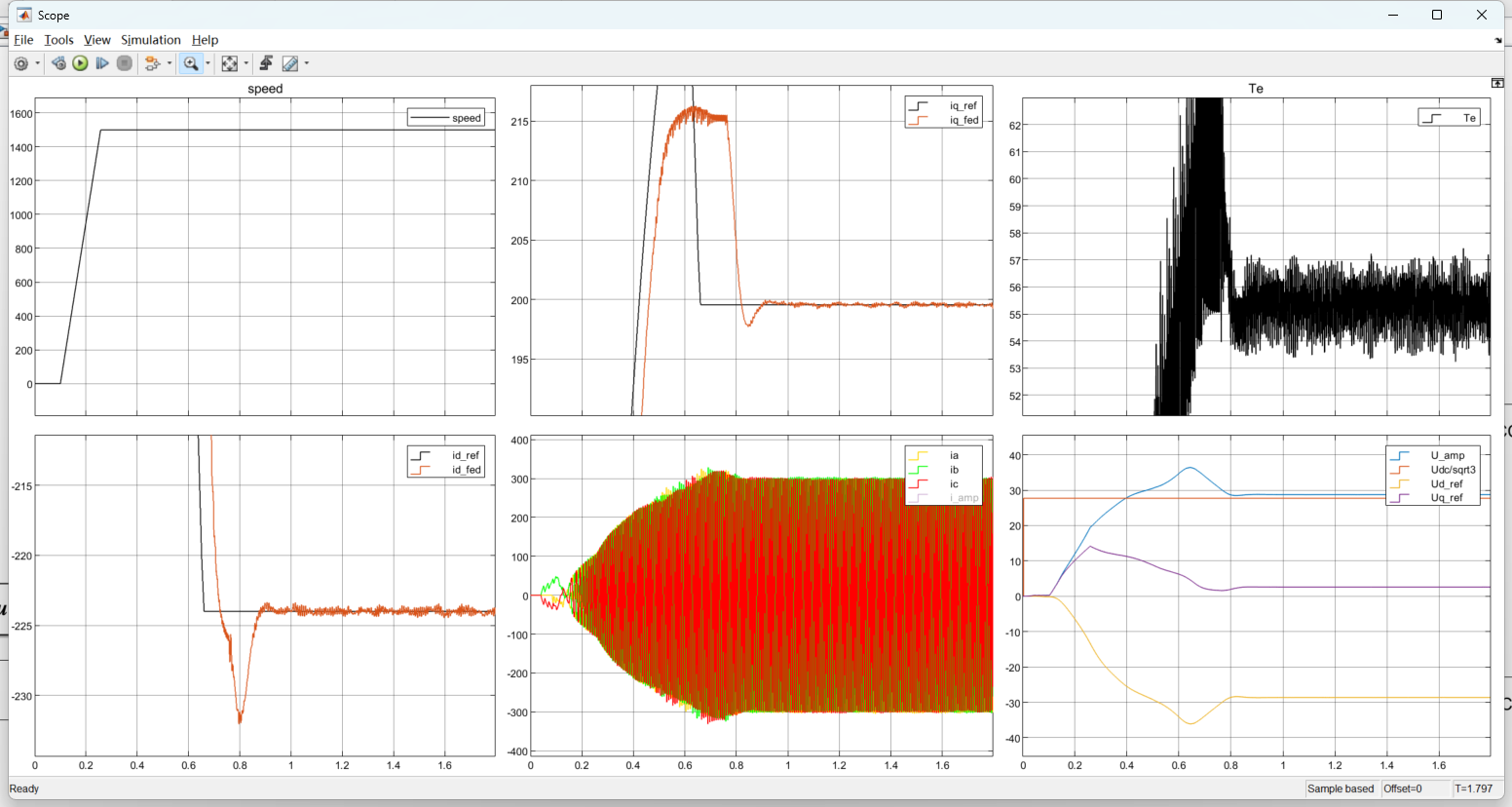
图7:1500Rpm&65Nm(限制id=-224)
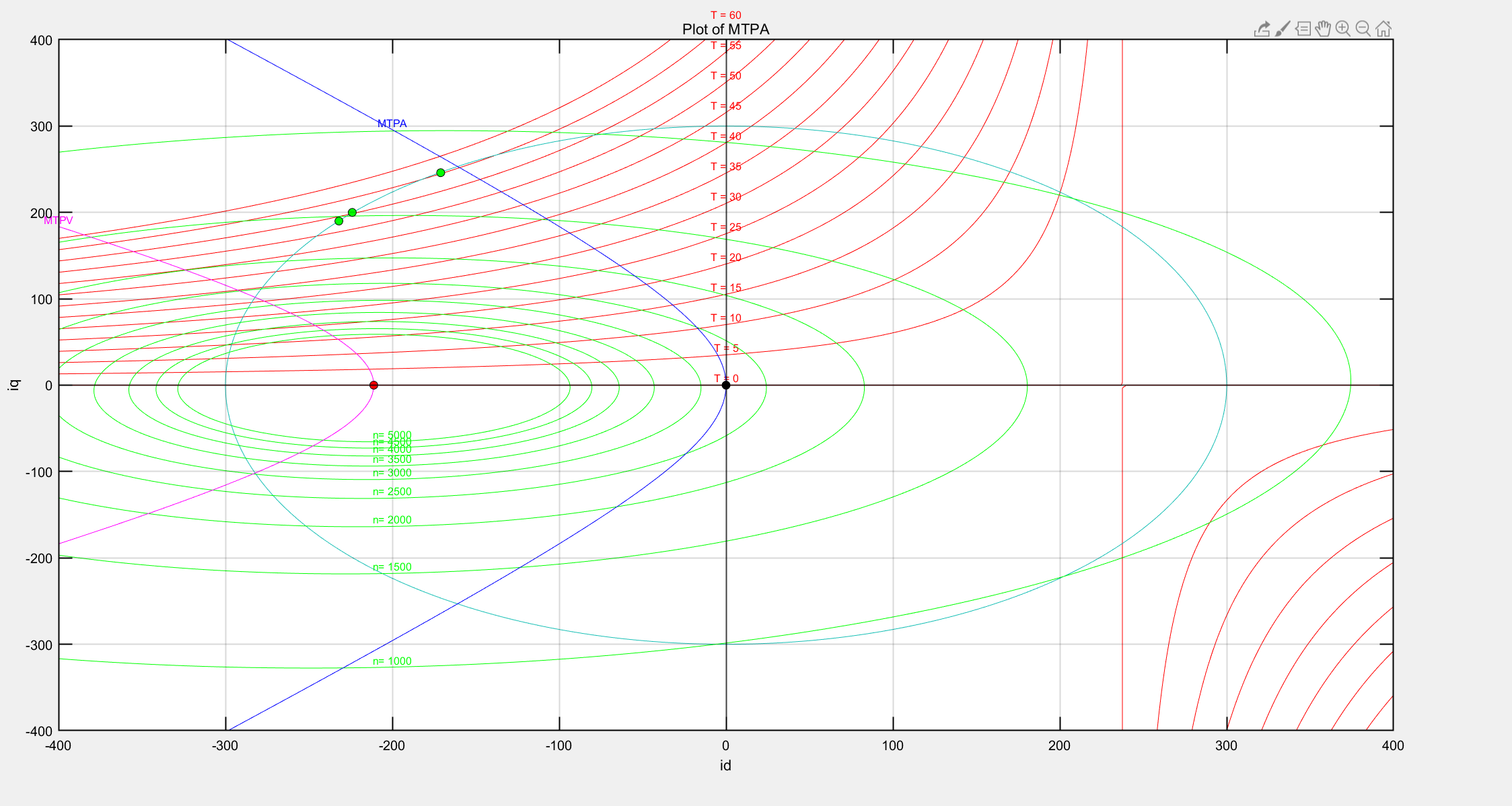
图8:1500Rpm&65Nm(限制id=-224)
虽然增大的转矩不多,但是这样限制之后,该点就正好落在了电压源和电流圆的交点上,此时转矩约为55Nm。为什么会这样,因为弱磁环并不是那么聪明,它只知道当电压超出电压限制后要减小id,但是由于系统和控制总是存在滞后,并不是id一减小,电压就立刻减小了,因此在系统闭环和反馈的调节下,id并不一定输出一个我们最想要的id,因此这个id需要我们手动做一些限制,比如在该工况下,将id限制为-224效果明显比它自己控制条街到-232的效果要好。
大家会不会很好奇,我怎么知道他是-224,这个当然可以用解析的方法解出来,更多都是试出来的,比如在-232附近上下调整,看看转矩能否增大,能增大就可以找到一个转矩的极大值点,此时对应的id就是我们想要限制的id。
这样,我们如果不对id进行限制,进一步增大转速到2000rpm
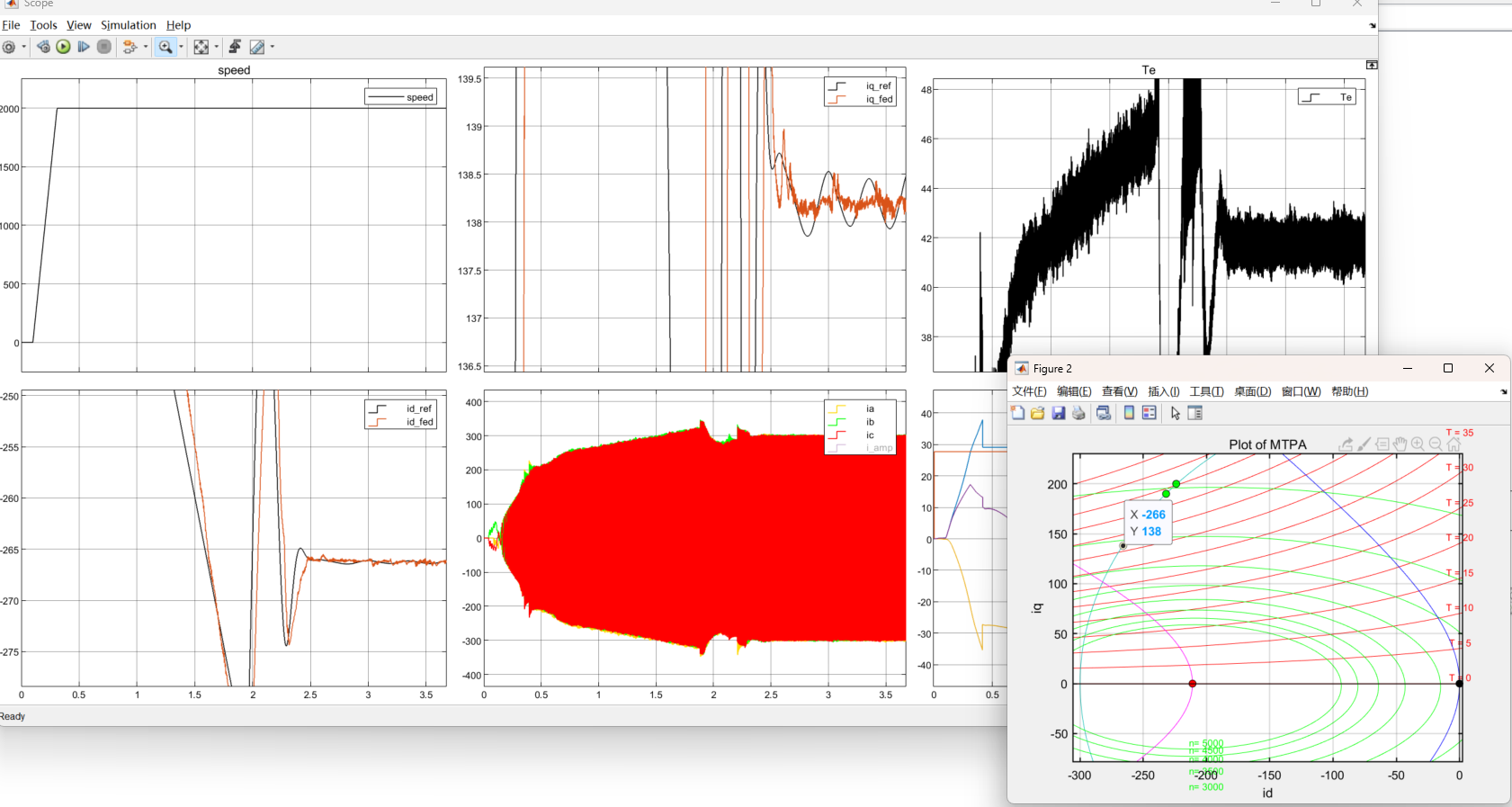
图8:2000rpm对应最大转矩点id=-266,iq=138
可以看到,此时依然不是最大转矩点,仅仅依靠弱磁环很难让系统工作到最大转矩点,因为此时系统并没有与电压环相交(实际上就是没有利用到过调制一区的那一部分电压,这里先挖个坑),如果我们限制id=-262,则可以获得一个更大的转矩,这里我不再啰嗦。
我们继续不限制id,增大转速到3000rpm
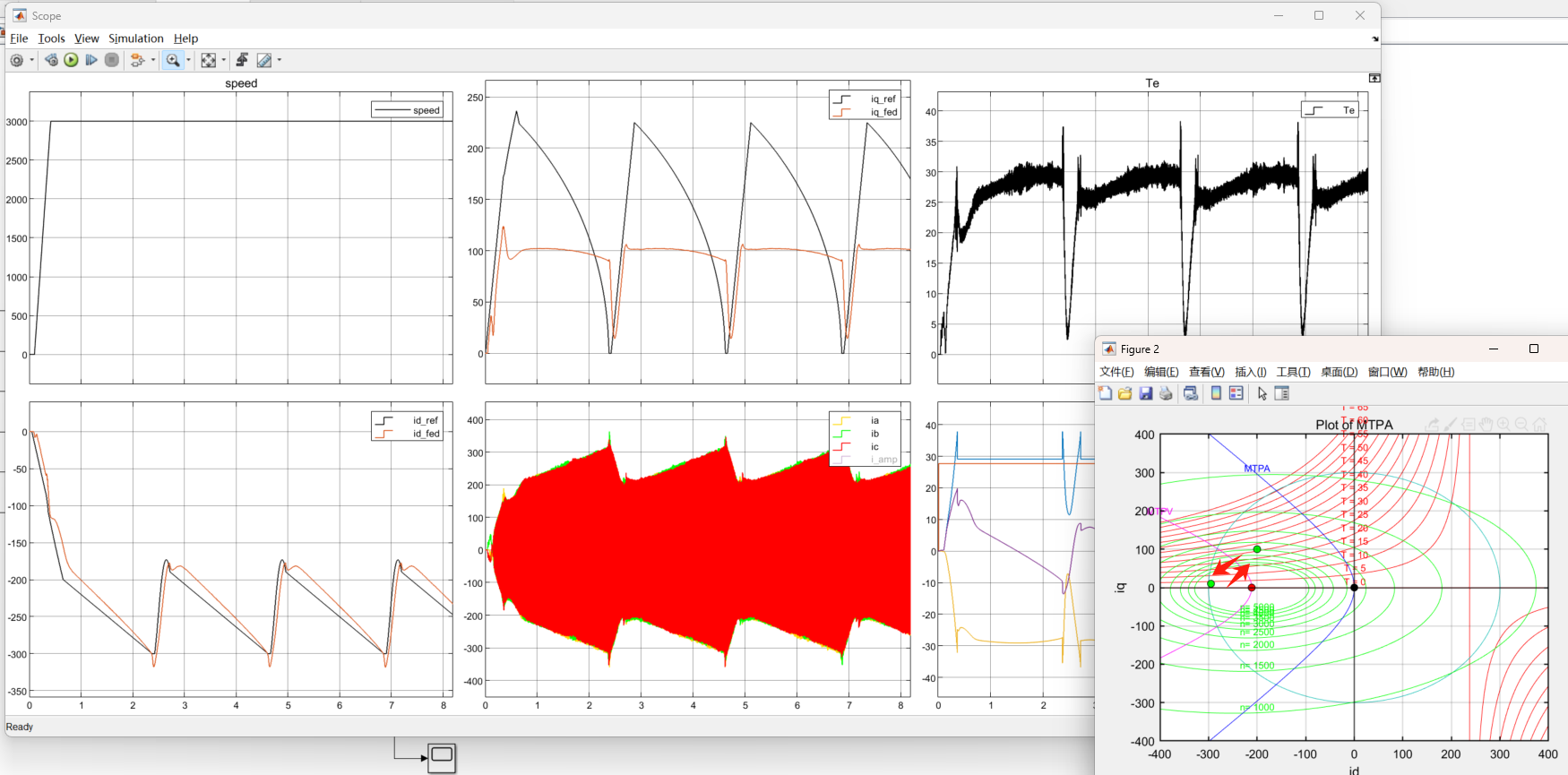
图9:3000rpm给最大转矩失控
哦豁,失控了,我们发现电流点一直在(-295,10)到(-200,100)之间震荡,系统已经不稳定了,按道理3000rpm的时候,系统的电流工作点应该要移动到MTPV曲线上,这里我们尝试把电流id限制到-276,
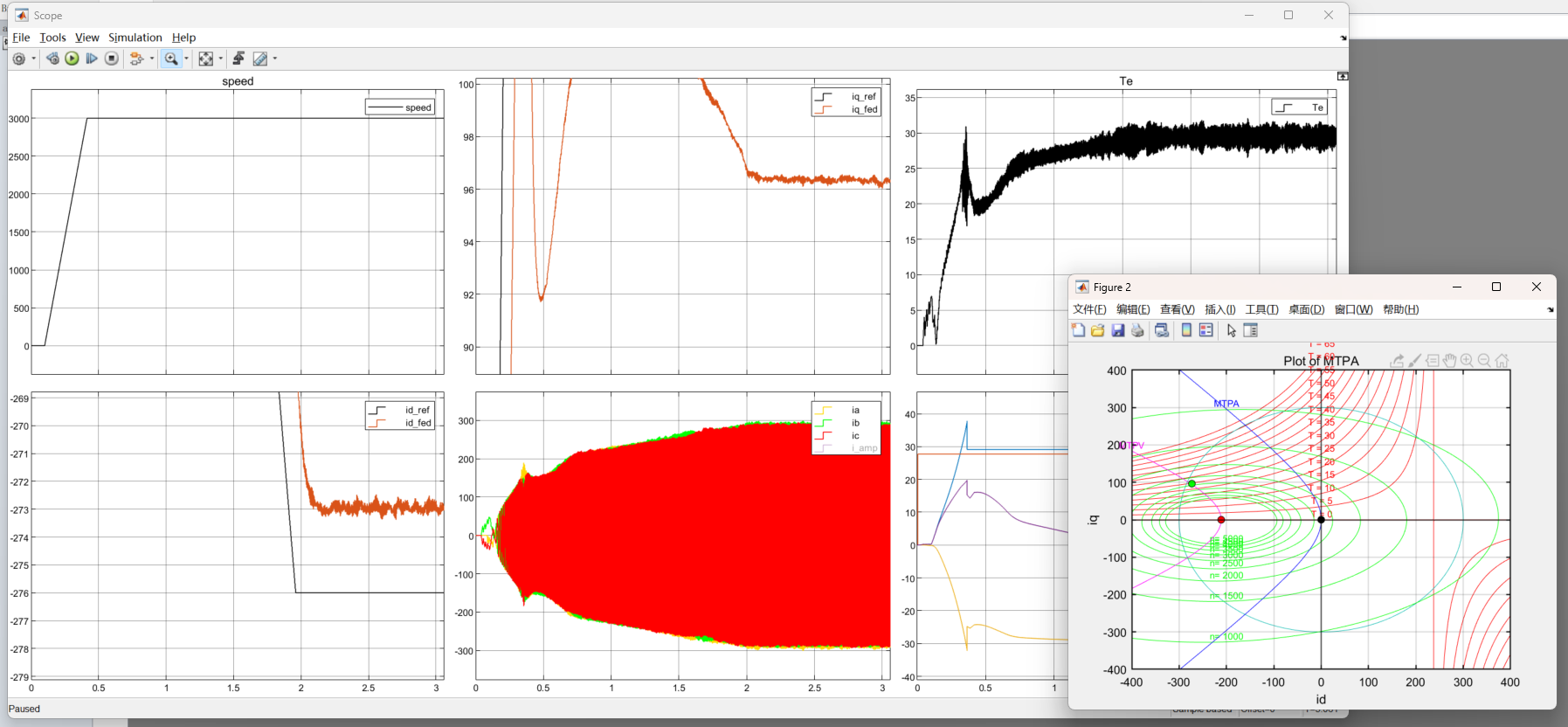
图10:3000rpm给最大转矩(限制id=-276)
可以看到,此时的id和iq实际值和参考值已经出现偏差了,但是即便如此,系统也控制的很稳定,并不会失控,且此时的电流工作点,也已经移动的MTPV上了,看起来除了电流没有跟踪上之外,一切并没有什么问题,对了,为什么电流环都没有跟踪上,系统依然很稳定没有失控呢?电流环没有跟上是正常的,因为我们请求扭矩都65Nm了,显然需求iq偏大,但是实际上系统出不到这么大的iq,自然也就跟不上了,这也侧面体现出内模控制的强大之处了,后续我会换成电流环pi控制,大家可以先猜猜会发生什么情况。
实际上我们通过解析的方法能算出此时的id和iq为-272,92.8,也可以画图用鼠标去找
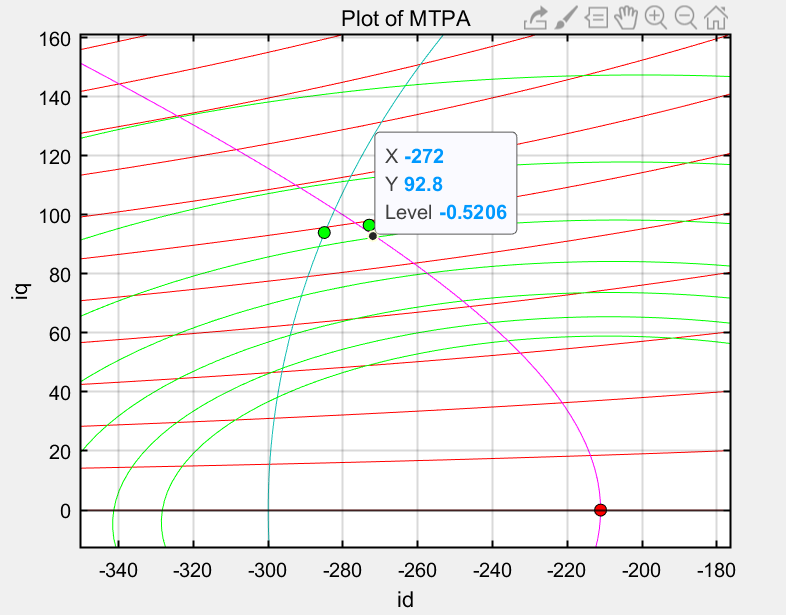
图11:3000Rpm对应MTPV曲线上的电流工作点
该工作点对应的转矩可以用转矩公式算出来约为28.3Nm,因此我们把id强制限制到-272,转矩请求改为28.3Nm,再看看仿真结果
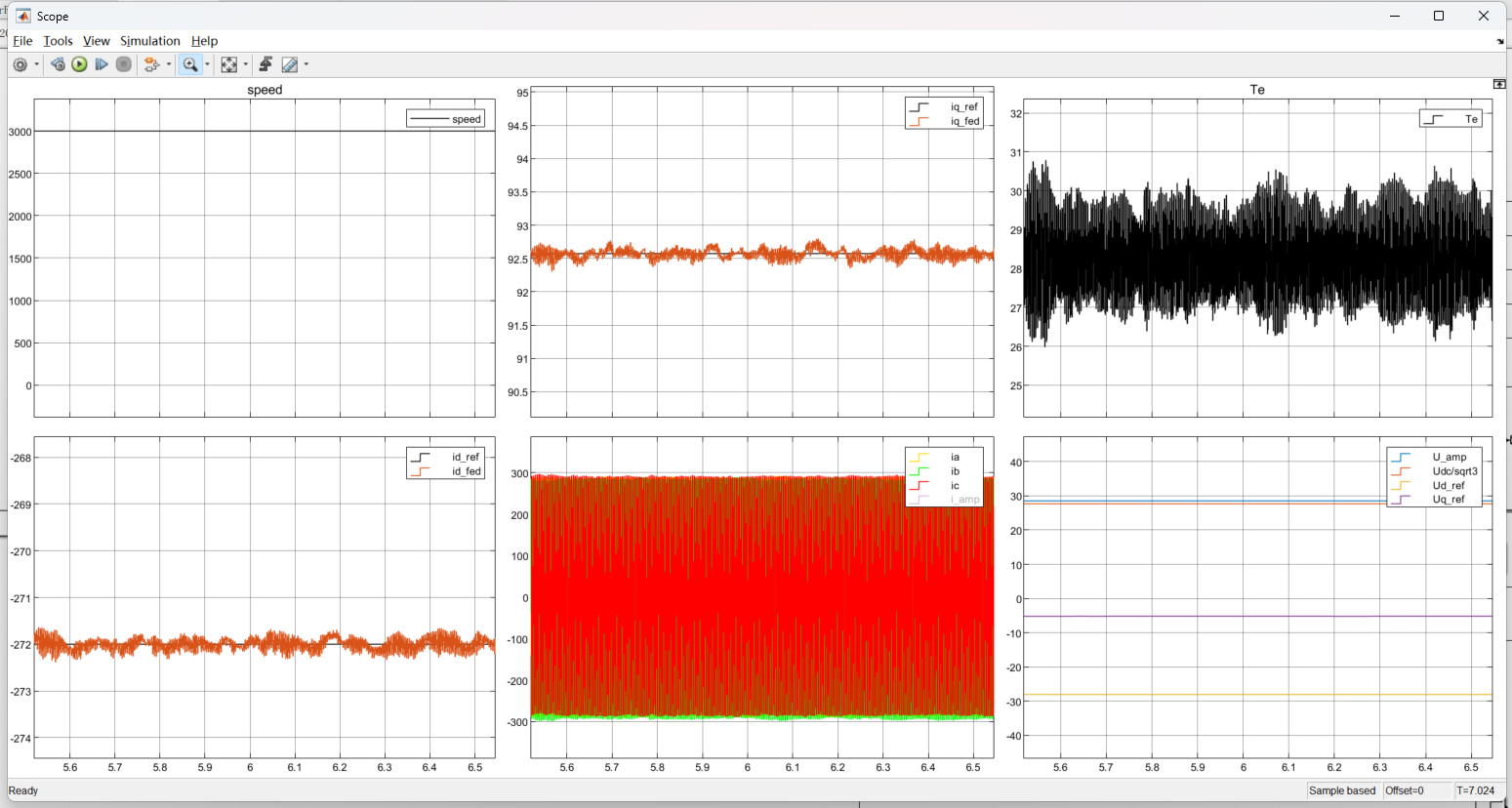
图12:3000Rpm对应MTPV曲线上的电流工作点
完美!此时虽然不是最大转矩的工作点(其实也差不多,实际根本不会纠结那么一点点扭矩),但是是最高效的。
更高的转速实际分析起来也是一样的,这里我就不再赘述了。我们回顾一下之前的问题
- 电流环PI的问题
如果我们该用电流环PI而不是内模控制
同样的3000Rpm下我们出最大扭矩,对id限制到-273,会发生什么事情?
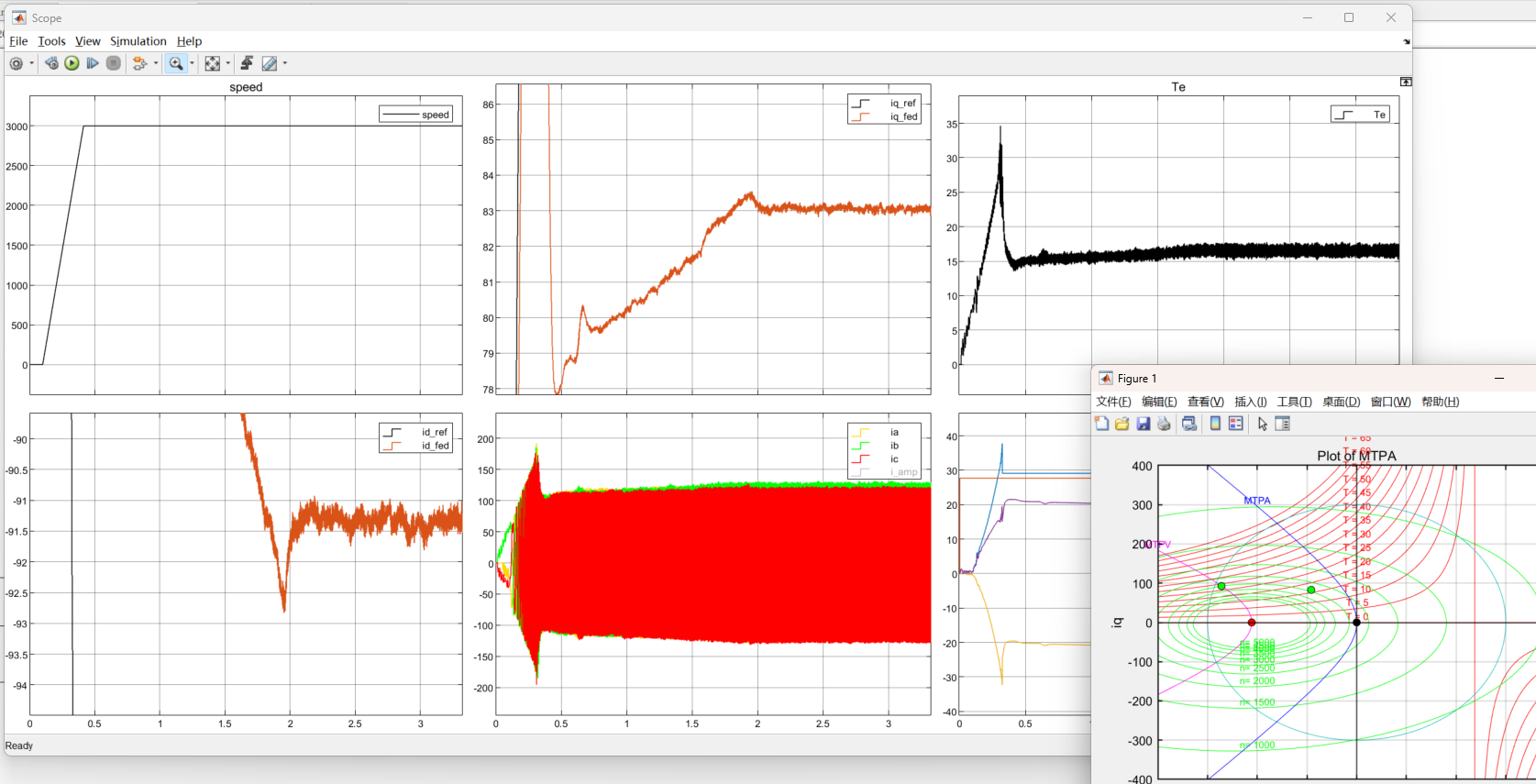
图13:电流PI控制3000rpm限制id-273
可以看到 这个时候的电流工作点为(-91.5, 83),与我们期望的(-272, 92.8)相去甚远,这大概就是内模控制的优势所在吧
六、结论与展望
- 本文结合实际,对MTPA和MTPV进行调试和仿真,实际上我们在控制过程中只要对id的最小值做一个查表限制即可
- 水平有限,这都是我粗浅的理解,欢迎大家讨论
- 感谢关注和点赞 您的支持是我更新的动力
- 以上 咸鱼可搜“离家出走的小蛤”
