[析]Deep reinforcement learning for drone navigation using sensor data
Deep reinforcement learning for drone navigation using sensor data 基于传感器数据的无人机导航深度强化学习方法
评价:MDP无记忆性,使用LSTM补足缺点。PPO解决新旧策略差距大的问题。
对于环境中的障碍物,设置增量课程,障碍物由1—>32.使用了PPO8, PPO16, PPO,和启发式算法(基准)作对比实验。PPO8和PPO16在训练初期学习速度较慢,但后期表现更稳定。随着训练进行,PPO8和PPO16的性能逐渐超越PPO,表明记忆机制的有效性。
LSTM的时间步数为4or8。输入一个长度为n的状态序列。每步的状态为[时间,障碍物信息,距离dx, dy]。LSTM输出的是策略(即 【动作,概率】),LSTM的优化不是通过标签,而是通过策略梯度函数优化。LSTM是网络结构,其算法结构是PPO. 其策略网络和价值网络共享LSTM参数,但其梯度不同,进行联合优化。
文章目录
- Deep reinforcement learning for drone navigation using sensor data 基于传感器数据的无人机导航深度强化学习方法
- 摘要
- 二、RL
- 2.1 MDP
- 2.2 Partially observable MDPs (POMDPs)
- 2.3 Policy gradients learning
- 2.4 Proximal policy optimisation (PPO) algorithm
- 2.5 PPO 代码
- 三、 Models and system architecture
- 3.1 Agents
- 3.2 Brains
- 3.3 Academy
- 3.4 Configuration
- 3.5 Curriculum learning
- 3.6 Memory
- 3.7 Training
- 四、实验
- 4.1实验评估: 对比算法
- 4.2 实验结果:训练过程分析
- 4.3 实验结果:性能对比
- 五、安全保障
- 5.1 安全保障:功能失效分析
- 5.2 安全保障:训练与模型验证
- 六、总结与展望
- 七、模型的实践
- 7.1 数据收集阶段
- 7.2 训练阶段
- 7.3 数据流图示
- 7.4 优化目标
- 7.6 PPO的约束机制'
- 7.7 LSTM的时序优化
- 7.8 LSTM+PPO的网络结构
- 7.9 策略网络与价值网络的关系
摘要
移动机器人,如 无人机(drone),可用于建筑物、基础设施和环境中的监视、监控和数据收集。准确且多方面的监测的重要性众所周知,可以早期发现并防止问题升级。这推动了对灵活、自主和强大决策能力的移动机器人的需求。这些系统需要能够通过融合来自多个来源的数据进行学习。直到最近,它们都是针对特定任务的。在本文中,我们描述了一种通用的导航算法,该算法使用无人机机载传感器的数据来引导无人机到达问题地点。在危险和安全关键的情况下,准确且快速地定位问题是至关重要的。我们使用近端策略优化深度强化学习算法 结合 增量课程 学习和长短期记忆神经网络来实现我们的通用且可适应的导航算法。我们通过启发式技术评估不同的配置以展示其准确性和效率。最后,我们考虑如何通过评估无人机在真实世界场景中使用我们的导航算法的安全性来保证无人机的安全。


二、RL
如上所述,我们使用局部算法进行导航,因为无人机只能看到探索空间的局部(它们是部分可观察的)。有许多局部导航方法。遗传算法可以执行部分可观测的导航[13]。它们生成一个随机生成的解决方案群体,并使用自然选择的原则来选择有用的一组解决方案。然而,它们倾向于陷入局部最小值。模糊逻辑算法[55]已被用于学习导航,Aouf等人[4] 表明他们的模糊逻辑方法优于三种元启发式(群体智能)算法:粒子群优化,人工蜂群和元启发式算法萤火虫算法,用于导航时间和路径长度。然而,在动态环境中,模糊逻辑算法难以应对,因为它们在环境变化时太慢而无法实时重新计算路径[46]。Patle等[38]综述了包括这些元启发式算法(如遗传算法和群体智能(包括粒子群优化、人工蜂群、飞蛾算法和蚁群优化)在内的多种技术,用于机器人导航。元启发式群体智能算法旨在通过智能方式探索模型空间来找到最佳模型。它们旨在找到一个好解决方案而不是最优解,并且可能陷入局部最小值。Patle等人[38]得出结论,遗传算法和群体智能可以在不确定的环境中导航,但它们复杂且不适合低成本机器人。常规神经网络如多层感知器可以用于训练导航模型[38, 46],但它们没有深度学习算法的计算能力,并且只能在更简单的环境中使用。导航算法可以使用深度分类学习与深度神经网络结合。深度神经网络通过生成带有标签的训练数据来学习导航,其中标签评估所选路径的质量[49]。然而,准确地标记足够多的训练样本既费时又困难。
相比之下,深度强化学习(deep RL)使用试错方法( error approac),在无人机导航时生成奖励和惩罚。这种深度RL的一个关键目标是产生能够在现实世界中进行经验驱动学习的自适应系统。Matiisen等人。[34]观察到深度RL已被用于解决电子游戏中的困难任务[35]、移动性[33, 44]以及机器人技术[31]。它还被用于机器人导航[56],作者们能够以62%的成功率在20x20的网格中导航。强化学习(RL)本身是一个自主的数学框架,用于经验驱动的学习[5]。正如Arulkumaran等人所指出的,[5],RL以前取得了一些成功,例如直升机导航[37],但这些方法不是通用的、可扩展的,并且仅限于相对简单的挑战。
2.1 MDP
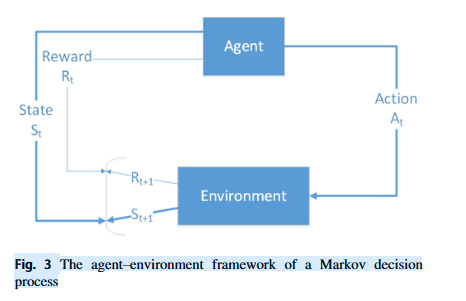
- 有限状态集S,加上起始状态分布p(s0)p(s_0)p(s0)。可能存在一个终端状态sT。学习任务的复杂度相对于定义状态所用变量的数量呈指数增长。我们稍后描述如何最小化状态表示
- 一组动作A,涵盖每个状态下可用的所有代理。我们只有一个代理可以向四个可能方向之一移动。
- 转换动态(策略)πθ(st+1∣st,at)\pi_{\theta}(s_{t+1}|s_t,a_t)πθ(st+1∣st,at),它使用参数集θ\thetaθ将时间t时的状态/动作对映射到时间t+1时的状态分布。
转换仅取决于当前状态和动作(马尔可夫假设) - 与每个转换相关的瞬时奖励函数R(st,at,st+1)R(s_t,a_t,s_{t+1})R(st,at,st+1);用于评估最优转换。
- 折现因子γ∈[0,1]\gamma \in [0,1]γ∈[0,1],这是未来奖励的当前值。它量化了即时奖励和未来奖励之间的重要性差异(较低的值更强调即时奖励)。
- 无记忆性。一旦当前状态已知,历史就被抹去,因为当前的马尔可夫状态包含了所有来自历史的有用信息;“在给定现在的情况下,未来与过去无关”。
我们将无人机导航问题类比于网格世界导航问题[48]。在本文中,我们知道无人机的GPS位置、无人机正前方N、E、S、W方向以及传感器读数在笛卡尔坐标系中的方向(x距离,y距离)(其中N、E、S和W相对于地面在这个例子中)。在现实场景中,我们可以使用相对于地面或相对于无人机的方向来确定传感器读数在极坐标系中的方向和幅度,具体取决于情况。幅度和方向可以轻松地从极坐标转换为笛卡尔坐标。如果有8个传感器以图4中所示的八角形排列,则最高传感器读数给出了相对于地面或无人机的方向,以及异常的幅度(强度)。这里无人机将朝东北方向飞行。

在我们的无人机导航推荐系统中,只有部分环境在任何时间点可观察。在现实世界中,我们只能通过无人机的避碰机制知道无人机的近似位置。我们不知道更远前方(在现实世界中它们可能被更近的障碍物遮挡)或超出无人机视野范围内的障碍物的位置。网格世界导航问题的替代公式将环境视为一幅图片(观察结果),其中网格中的每个单元映射到一个像素值,表示该单元的内容{空、障碍物、目标}[50]。这需要环境的完整信息,而无人机无法提供。此外,这种方法不能扩展到不同的网格大小,因为它使用N x N网格作为图像来学习导航。在16 x 16观察网格上训练的深度学习器不能用这种观察公式推广到32 x 32网格,因为网络输入尺寸不同(16 x 16与32 x 32),并且会错位。我们的公式是可扩展、适应和灵活的。
2.2 Partially observable MDPs (POMDPs)
无人机不可能看到全局地图,它只能感知到自己周围的局部信息,这就是所谓的部分可观测(POMDP)。
为了使用这种部分(局部)信息训练无人机,我们使用了一种称为部分可观测马尔可夫决策过程(POMDPs)的MDPs的泛化。
在POMDP中,代理接收一个观察值ot∈Ωo_t\in \Omegaot∈Ω,其中观察值的分布P(ot+1∣st+1,a)P(o_{t+1}|s_{t+1},a)P(ot+1∣st+1,a)取决于先前的动作a t和当前状态st+1s_{t+1}st+1 。这里,观察值由一个依赖于当前状态{传感器方向,传感器幅度,N,E,S,W空间}和之前应用的动作(无人机是否移动了N,E,S,W)的状态空间模型中的映射来描述。
MDP表示从一个状态到另一个状态的转移概率。策略π\piπ是在给定状态下的行动分布πθ(at∣st)=P[At=at∣St=st]\pi_{\theta}(a_t|s_t)=P[A_t=a_t|S_t=s_t]πθ(at∣st)=P[At=at∣St=st]Š。
策略完全定义了在当前状态下代理的行为;它根据当前状态sts_tst生成一个动作ata_tat,并且该动作在执行时产生一个奖励rtr_trt。
RL的目标是识别最优策略π∗\pi^*π∗,该策略最大化所有状态下的奖励(即最大化期望奖励值E):π∗=arg maxπE[Rt∣π]\pi^*=\argmax _{\pi}E[R_t|\pi]π∗=argmaxπE[Rt∣π]。确定最优策略有两种常见的方法:价值学习,它维护一个价值函数模型;以及无模型的策略学习,直接搜索最优策略。
在本文中,我们使用策略学习。价值学习在每次迭代时考虑所有动作,并且很慢;它的执行时间是策略评估的 |A| 倍。此外,策略在每次迭代时不会改变,浪费了更多的时间。
2.3 Policy gradients learning

与许多其他AI算法一样,RL的缺点是内存使用、计算复杂性和样本复杂性。最近,人们开始用 深度神经网络(DNN)来支持RL,这提供了强大的函数逼近和表示学习特性。深度RL算法的一个子集是策略梯度算法。它们通过沿着策略的梯度上升来寻找策略质量的局部最大值。策略梯度学习是稳健的,但梯度方差很高。为了降低这种方差,我们使用梯度的无偏估计,并减去几个回合的平均回报作为基线。此外,策略梯度具有较大的参数集,这可能导致严重的局部最小值。为了最小化局部最小值的可能性,我们可以使用信任区域(rust regions.)。信任区域搜索通过约束优化步骤,使它们位于真实成本函数近似仍然有效的区域内。我们可以通过确保更新后的策略与先前的策略有低偏差来减少非常差的更新可能性,使用Kullback–Leibler (KL)散度[29]来衡量当前和提议策略之间的偏差。信任区域策略优化(Trust region policy optimisation)(TRPO)通过限制策略可以改变的幅度并保证其单调改进,证明了其鲁棒性。然而,这种受限优化需要计算二阶梯度,这限制了其适用范围。为了克服这一点,Schulman等人[45]开发了近端策略优化(PPO)算法,该算法执行无约束优化,仅需要一阶梯度信息。PPO执行多次随机梯度下降以进行每次策略更新。因此,它以与随机梯度下降兼容的方式进行信任区域更新,从而通过消除自适应更新的需要简化了算法。在每个时间步t处计算更新,该更新最小化成本函数,同时确保与先前的策略的偏差相对较小。
2.4 Proximal policy optimisation (PPO) algorithm
PPO的核心思想是在更新策略时,限制新策略与旧策略之间的差异,确保每次更新都在一个相对安全的区域内进行,避免策略发生剧烈变化导致性能下降。这就像开车时平稳加速,而不是猛踩油门。PPO通过裁剪重要性比率来实现这一点,既保证了学习效率,又提高了训练的稳定性。

💡小分析
新策略是通过梯度下降法从旧策略产生的。PPO算法在每次迭代时计算策略梯度,然后使用梯度下降来更新策略参数θ,从而得到新策略πθπ^{θ}πθ
Why 新旧策略差异会很大?
在强化学习中,策略更新是通过梯度计算进行的,但梯度方向可能很"激进"(特别是当奖励信号稀疏或噪声较大时)。
如果直接按梯度方向大幅更新策略(比如用较大的学习率),新策略可能会与旧策略产生显著差异,导致:
- 策略崩溃:新策略可能完全偏离之前学到的有效行为
- 训练不稳定:过大的更新会导致策略性能剧烈波动
为什么需要信任区域(Trust Region)
信任区域的核心思想是:限制每次策略更新的幅度,确保新策略不会偏离旧策略太远。PPO通过两种机制实现:
- 重要性比率裁剪:强制比率rt(θ)保持在[1-ε,1+ε]范围内,本质上限制了策略更新的最大步长
- KL散度约束(在TRPO中显式使用):从数学上保证新旧策略的KL散度不超过阈值
裁剪重要性比率是PPO算法的核心操作,具体包括:
- 计算重要性比率:rt(θ)=πθ(at∣st)/πoldθ(at∣st)r_t(θ) = π^θ(a_t|s_t)/π^θ_{old}(a_t|s_t)rt(θ)=πθ(at∣st)/πoldθ(at∣st)
- 对重要性比率进行裁剪:clip(rt(θ),1−ε,1+ε)(r_t(θ), 1-ε, 1+ε)(rt(θ),1−ε,1+ε)
- 取裁剪前后比率的最小值作为最终目标函数
其中ε是超参数(通常设为0.1或0.2),用于限制策略更新的幅度。假设旧策略以90%概率选择动作A,10%选择B。如果新策略突然变成10%A、90%B(由于一次激进的梯度更新),这样的剧烈变化可能导致:
- 之前积累的经验数据(基于旧策略)对新策略不再适用
- 策略需要重新探索,降低学习效率
PPO方法
PPO的目标是解决传统策略梯度方法(如REINFORCE或TRPO)的两大问题:
- 步长敏感:更新幅度过大可能导致策略崩溃(性能骤降)。
- 样本效率低:需要大量交互数据。
PPO通过以下设计实现稳定更新:
- “信任区域”的近似:用**裁剪(Clipping)**机制代替TRPO的复杂二阶优化约束。
* 重要性采样:利用旧策略的数据高效计算新策略的梯度。
2.5 PPO 代码
class PPOAgent:def __init__(self, policy_net, lr=3e-4, clip_eps=0.2):self.policy = policy_net # 1. 策略网络 πθ(a|s)self.optimizer = torch.optim.Adam(self.policy.parameters(), lr=lr)self.clip_eps = clip_eps # 2. ε:PPO 的裁剪阈值def update(self, states, actions, old_log_probs, advantages):# 3. 对同一批数据做 K_EPOCHS 次小批量梯度上升for _ in range(K_EPOCHS): # K_EPOCHS 通常 10~30new_log_probs = self.policy(states).log_prob(actions) # 4. 前向:拿新的 log πθratio = (new_log_probs - old_log_probs).exp() # 5. 重要性采样系数 r_t(θ)surr1 = ratio * advantages # 6. 未裁剪的目标surr2 = torch.clamp(ratio,1-self.clip_eps,1+self.clip_eps) * advantages # 7. 裁剪后的目标loss = -torch.min(surr1, surr2).mean() # 8. PPO-Clip 的目标函数取负号(因为 PyTorch 只能最小化)self.optimizer.zero_grad()loss.backward() # 9. 反向传播self.optimizer.step()| 行号 | 代码 | 含义 | ||
|---|---|---|---|---|
| 1 | policy_net | 一个 torch.nn.Module,输入状态 s,输出动作分布。连续动作常用 Normal(mean, std);离散动作常用 Categorical(logits)。 | ||
| 2 | clip_eps=0.2 | PPO 论文默认 0.1~0.3。它决定了「策略一次不能更新太多」。 | ||
| 3 | for _ in range(K_EPOCHS) | 用同一批 rollout 数据反复训练多次。提高样本利用率,同时因为数据固定,梯度方差小。 | ||
| 4 | log_prob(actions) | 对新网络 πθ 再跑一次前向,得到当前策略下这批动作的对数概率 logπθ(at∣st)log πθ(aₜ| sₜ)logπθ(at∣st)。注意 不重新采样动作,而是用 rollout 里已经做过的动作。 | ||
| 5 | ratio = (new_log_probs - old_log_probs).exp() | 计算重要性采样权重:r_t(θ)=π_θ(a_t∣s_t)π_θ_old(a_t∣s_t)r\_t(\theta)=\frac{\pi\_\theta(a\_t | s\_t)}{\pi\_{\theta\_{\text{old}}}(a\_t | s\_t)} r_t(θ)=π_θ_old(a_t∣s_t)π_θ(a_t∣s_t)这里用对数相减再 exp,数值稳定。 | ||
| 6 | surr1 = ratio * advantages | 未裁剪的目标:鼓励提高 advantage>0 的动作概率,降低 advantage<0 的动作概率。 | ||
| 7 | surr2 = torch.clamp(...) | 把 ratio 强行限制在 [1-ε, 1+ε] 区间内,防止策略一步迈太大。 | ||
| 8 | loss = -torch.min(...).mean() | 取 min(surr1, surr2) 再平均,最后加负号变成「损失」让优化器去最小化。 | ||
| 9 | backward() & step() | 普通梯度下降。 |
三、 Models and system architecture
我们的无人机仿真使用Unity 3-D的ML-agents框架[26]来设计、开发和测试仿真,然后在实际部署之前进行测试。ML-agents使用Unity 3-D#开发框架作为前端和中间件接口,与Google TensorFlow[1]后端通过Python连接。MS Windows版本的ML-agents有一个DLL库,用于C#和Python之间的接口。它允许用户开发训练智能代理的环境[26]。在本文中,我们专注于2-D导航,并且不考虑无人机的高度。因此,我们的异常检测问题是使用Unity3-D ML-agents中的网格世界实现的确定性、单代理搜索、POMDP问题。我们指定网格大小和障碍物数量,并随机生成网格(参见图5以获取示例网格)。Unity 3-D游戏环境运行模拟。我们的系统包括三个主要交互过程。


💡了解socket
在 Unity ML-Agents 框架中,Socket(套接字)通信 用于连接 Unity 环境(C#)和 Python 训练后端(TensorFlow/PyTorch),使两者能够实时交换数据。以下是它的工作原理和关键点:
- Socket 通信的作用
- Unity(C# 端) :负责环境模拟(如无人机导航的网格世界)、状态(State)采集、动作(Action)执行。
- Python(训练端) :运行强化学习算法(如 PPO),接收状态,计算动作,并返回给 Unity。
- 通信方式:通过 TCP/IP Socket 实现跨语言、跨进程的数据交换。
- 通信流程
- Unity 启动 Socket 服务端
- Unity 在训练模式下会启动一个 Socket 服务端,监听特定端口(默认 5005)。
服务端代码在 Unity 的 Academy 类中实现(ML-Agents 的核心协调模块)。- Python 客户端连接
- Python 通过 mlagents.train 模块启动训练时,会主动连接 Unity 的 Socket 服务端。
连接成功后,双方通过约定的协议交换数据。
- 数据交换内容
- Unity → Python:
- 发送当前状态(State):如无人机周围的障碍物信息、目标距离等(N, E, S, W, x-dist, y-dist)。
- 发送奖励(Reward):上一步动作的即时奖励。
- Python → Unity:
- 返回动作(Action):如移动方向(N, E, S, W)。
- 其他控制指令(如重置环境)。

3.1 Agents
在ML-agents框架中,代理Agents [智能体]是Unity 3-D游戏对象,如[10, 11, 32]和[54]中所示。在我们的模拟中,代理是一架无人机。在ML-agents中,代理生成状态,执行指定的动作并分配累积奖励。代理与一个大脑(第3.2节)链接。
代理(无人机)采取指定动作(向北、东、南或西移动一格),以导航网格,避开障碍物并找到目标。我们的状态空间是一个长度为6的向量,包含相邻网格单元的内容(N, E, S, W),以及到目标(异常)的x距离和y距离。这既紧凑,可扩展又现实。
(在真实世界中,无人机只能感知其局部环境;由于遮挡,它不能保证前方可见。)
在我们的RL中,代理每次移动都会收到一个小惩罚,到达目标时获得正奖励(+1),与障碍物碰撞时获得负奖励(-1)。
3.2 Brains
每个代理都有一个与之相连的脑,提供智能并决定行动。大脑为代理做出决策提供逻辑;它在每次情况下确定最佳行动。
我们的大脑使用由OpenAI开发的近端策略优化(PPO)RL算法[45],该算法针对实时环境进行了优化。
ML代理的PPO算法在TensorFlow中实现,并在一个单独的Python进程中运行(通过套接字与正在运行的Unity应用程序通信)。PPO算法接收状态空间表示(相邻网格单元的内容(N、E、S、W),以及x距离和y距离)和可能的动作集(向N、E、S或W移动一个单元格)作为输入,并选择使用学习到的策略来最大化奖励的动作。
3.3 Academy
环境中的这个元素协调决策过程。它在大脑(逻辑)和实际的Python TensorFlow实现之间形成了一条管道,后者将逻辑作为学习到的深度神经网络模型以程序化方式包含其中。
3.4 Configuration
为了配置代理和大脑,我们花费了很长时间评估不同的代理、状态、奖励配置。这些设置是成功实现的关键,因此值得花时间评估不同的配置。我们分析了:
- 不同的状态表示,特别是不同的距离表示,我们使用了与网格大小和剩余距离相关的不同缩放因子。我们发现最佳结果来自使用N、E、S、W、d(x),d(y)的状态空间。
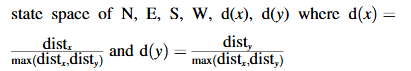
- 不同的步奖励,我们使用了与网格大小相关的不同缩放因子发现一个步的惩罚

- 我们尝试了多种PPO的超参数组合,发现最好的结果来自“附录”中列出的设置。


如果我们使用训练网格中的1个障碍物来训练代理,那么代理将学会直接前往目标,这是理想的。然而,在训练和评估期间,当遇到更复杂的障碍物(2或更多红十字交叉)时,它会挣扎。如果我们在开始训练时使用多个障碍物,例如32个障碍物(随机放置的红十字),则它会学会随意行走。这使它能够克服更复杂的障碍物,但在网格世界环境中障碍物很少时,它不会直接前往目标。
这存在一个问题,消除了我们希望代理是通用的并能够应对各种环境的愿望。因此,我们观察了接下来描述的逐步(课程)学习。
💡思考
这就涉及到一个问题,人工智能(如强化学习)训练中,障碍物的数量或比例 会显著影响训练效果和最终策略的性能。以下是关键影响因素及其作用机制:
- 障碍物数量/比例的影响
(1) 训练难度与泛化能力
- 低障碍物密度(简单环境):
无人机容易找到直达目标的路径,训练速度快。但学到的策略可能过于简单,无法应对复杂场景(如现实中的密集障碍)。
风险:策略过拟合到简单环境,泛化能力差。- 高障碍物密度(复杂环境):
训练初期难度大,无人机容易陷入局部最优(如绕圈或反复碰撞)。但最终学到的策略更鲁棒,能适应动态或未知环境。
典型问题:稀疏奖励问题(长时间无正向反馈)。探索效率低(需更多训练步数)。
(2) 障碍物分布形态
规则障碍(如网格) :策略可能学会特定“套路”(如贴墙走)。
随机障碍:迫使策略学会通用避障逻辑,但训练更耗时。
动态障碍(如移动障碍物):需引入记忆(如LSTM)或在线适应机制。作者通过 渐进式课程学习(Incremental Curriculum Learning) 解决障碍物数量/比例的影响:
- 分阶段训练:
从简单环境(如1个障碍)开始,逐步增加障碍物数量(1 → 4 → 8 → 16 → 32)。
每阶段训练到策略稳定后(通过平均奖励判断),再进入下一阶段。- 平衡探索与利用:
早期阶段快速学会基础导航(如直线趋近目标)。
后期阶段专注复杂避障(如绕行凹形障碍)。- 实验数据支持:
直接训练32障碍的环境时,策略收敛慢且易学“无意义随机游走”。
课程学习后的策略在测试中表现更优(见表1/2,PPO₈在32障碍环境成功率更高)。其他优化方法
(1) 奖励函数设计
- 稀疏奖励改进:
- 添加基于距离的中间奖励(如每步靠近目标给予小奖励)。
- 惩罚无效动作(如反复撞墙)。
- 课程学习 + 动态奖励:
早期阶段侧重“到达目标”,后期阶段增加“路径效率”权重。(2) 记忆机制(LSTM)
- 应对复杂障碍:
- LSTM记忆过去几步的状态,避免重复探索无效路径(如死胡同)。
- 论文中LSTM长度8比16更优(过长记忆反而干扰短期决策)。
(3) 障碍物比例建议
- 训练初期:障碍物占比 ≤ 10%(如16×16网格中10~20个障碍)。
- 最终阶段:可提升至30%~50%(模拟极端场景)。
- 动态调整:根据训练指标(如碰撞率)自动调整障碍密度。
3.5 Curriculum learning

课程学习从一个简单的任务开始,随着学习的进行逐渐增加任务的复杂性,直到我们达到感兴趣的训练标准。它不会忘记之前学过的实例。每次课(训练标准)在训练期间生成一组不同的权重,基于先前的权重。我们从1个障碍物到4个然后是8个,接着是16个,最后是32个,都在一个16x16的网格中。在这个序列结束时,无人机仍然可以高效地导航16x16网格中的1个障碍物,因为网络没有忘记在第一节课中学到的知识。它现在能够利用在最后的课程中学到的知识,高效地导航16×16格中的32个障碍物。
在本文中,我们使用一种自适应课程学习方法,称为“增量式课程学习incremental curriculum learning’’”。课程学习需要预先指定每节课的迭代次数,例如训练第一节课5百万次。通常,这个数字无法提前准确确定。
增量式课程学习允许用户根据优化训练调整每节课的迭代次数。它在预指定的迭代次数内训练网络,除非用户提前停止学习过程,如果模型已经充分训练,则无需额外迭代;如果模型未在预指定的迭代次数后得到足够训练,则增加额外迭代。有许多指标可以用来确定每个课程需要训练多少个epoch,例如损失、熵或最终平均奖励。
我们分析了这些指标,并发现最终平均奖励生成了最佳的导航模型,适用于我们的增量式课程学习。其他指标往往导致模型过度训练或训练不足,从而导致泛化能力差。因此,我们使用平均最终奖励来确定每节课何时应结束。
例如,如果我们指定训练课程一为5百万次迭代,并检查代理的平均最终奖励(每隔10,000次训练迭代进行平均),我们可以确定奖励是否仍在增加还是已经稳定。如果它仍在增加,那么我们假设代理没有足够地学习这个课程步骤,并且可以在第一课中再添加0.5百万次迭代,并在运行了5.5百万次迭代后再次测试。因此,我们逐步学习每一课,直到我们确信PPO已经充分地学会了这节课,然后我们进入下一节课(课程中的更复杂任务)。我们在本节5的评估中进一步分析这种增量式课程学习。
训练一个复杂的AI模型,不能一开始就扔给它最难的任务,否则它会圈。
3.6 Memory
在第2节中,我们正式定义了一个MDP。我们强调了MDPs是无记忆的。这成为我们的导航推荐系统的一个问题。
当代理遇到凹陷障碍物(死胡同)时,缺乏记忆是一个问题。PPO代理无法记住之前的移动而来回走或反复圈转。为了克服这个问题,我们在PPO深度学习中添加了一个LSTM记忆层,如图6所示。LSTM是一种特殊的递归神经网络[20],能够学习更长的依赖关系(序列),使其非常适合为代理提供一个记忆层。
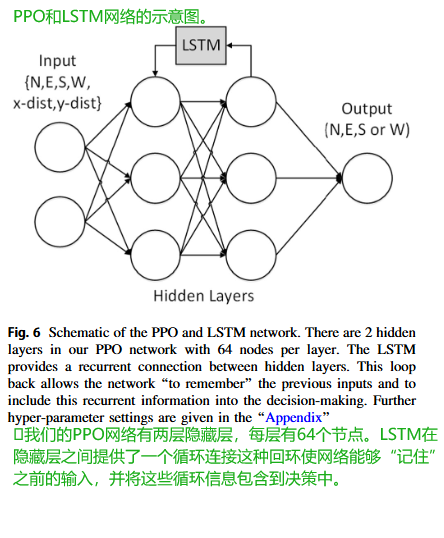
LSTM网络由称为单元cells的内存块memory blocks组成。这些单元形成序列,并负责记忆和记忆操作,以更新隐藏状态(记忆)。每个单元都有门控机制,因此可以存储或删除信息(通过打开和关闭门)。因此,LSTM可以从其记忆中读取、写入和删除信息。序列长度是代理必须记住的步骤数。它也是输入数据和在训练期间通过LSTM传递的序列的长度。这个长度需要足够长,以捕获代理必须记住的信息。
然而,较长的序列会增加训练时间,因为这增加了LSTM的复杂性。在这种情况下,我们需要记住足够的步骤,使代理能够导航死胡同和其他更复杂的障碍物。LSTMS是递归的,并且通过时间和层反向传播输出误差。这种递归机制允许此类网络在时间步长上学习。
💡如何使用LSTM呢?
在论文描述的PPO+LSTM框架中,每个时间步的输入包含两部分:
- 当前状态观测(State):[N, E, S, W障碍信息, x-distance, y-distance] (例如:[0, 1, 0, 0, 3.2, -1.5] 表示东侧有障碍,目标在东北方向)
- 历史状态序列:
LSTM会接收过去 n 个时间步的状态(如 n=8),形成时间维度。💫时间序列的生成方式
- 滑动窗口:
每次输入是一个长度为 n 的状态序列,例如:[[t-7: N, E, S, W, x, y], # 8步前的状态[t-6: N, E, S, W, x, y], ..., [t: N, E, S, W, x, y] # 当前状态 ]
- 实际实现:Unity ML-Agents 会自动缓存历史状态,按LSTM长度 (sequence_length) 打包成序列输入。
💫为什么需要时间序列?
- 解决部分可观测性(POMDP):单步观测无法判断凹形障碍(如U型墙),需记忆过去路径。
- 避免循环行为:通过历史状态识别“绕圈”或“反复撞墙”等无效动作。
💡LSTM的输出:动作决策
(1) 输出内容
- 策略分布(Policy):LSTM输出的是当前状态下各动作的概率分布(如 [N:0.7, E:0.1, S:0.1, W:0.1])。通过Softmax层实现多分类。
- 状态价值估计(Value):附加一个线性层输出标量,表示当前状态的长期回报预测(用于PPO的优势函数计算)。
(2) 输出与动作的关系 :PPO的决策流程:
- LSTM处理时间序列状态 → 生成动作概率
- 按概率采样动作(训练时)或选最高概率动作(测试时)
- 执行动作后,新状态加入序列,更新LSTM隐藏状态
(3) 输出示例
# 假设LSTM输出层结构: output = {'action_probs': [0.7, 0.1, 0.1, 0.1], # 对应[N, E, S, W]'value': 0.85 # 当前状态价值 }
3.7 Training
在训练期间,带有LSTM序列记忆的TensorFlow PPO模型执行决策。TensorFlow模型与Unity环境分离并通过套接字通信。我们使用增量课程学习训练了大脑5000万次训练。每个场景由Unity3-D独立生成,作为单独的导航任务。对于每个网格(场景),导航器要么解决网格,要么失败或超时。然后它继续到下一个网格布局。使用Unity 3-D C#随机数生成器在网格中放置障碍物以选择位置。PPO网络设置如图6所示,Unity ML-Agents的参数集见“附录”。网络输入为六维状态向量(N, E, S, W, x-距离, y-距离),输出为采取的动作:向N、E、S或W移动一步。
💡 与PPO的协同工作
(1) 训练时的数据流
- 序列采样:
- 从经验回放缓存中抽取长度为 n 的连续状态-动作-奖励序列。
- 序列需对齐,避免时间错位(ML-Agents 自动处理)。
- 梯度更新:
- LSTM的隐藏状态在序列内传递,但不同序列间重置。
- PPO的损失函数(含策略裁剪)同时优化LSTM和全连接层。
(2) 超参数设置
关键参数(论文附录):LSTM:sequence_length: 8 # 时间步数(记忆长度)hidden_units: 64 # LSTM隐藏层维度num_layers: 1 # 堆叠层数
- 长度选择依据:
过短(如4):无法记住绕行路径。
过长(如16):训练慢且引入噪声。
论文中 8 是平衡点(足以应对多数凹形障碍)。
💡 LSTM通常用于有监督学习,存在标签。那么在强化学习中没有标签,如何优化呢???优化流程如下:
(1) 策略梯度(Policy Gradient)驱动
- LSTM的输出是策略分布(动作概率),即 π(a∣s,h)π(a|s, h)π(a∣s,h),其中 h 是LSTM的隐藏状态。
- 优化目标:通过策略梯度定理,直接调整LSTM的参数,使得高奖励的动作概率增加,低奖励的动作概率降低。
梯度公式(简化版):(2) PPO的裁剪机制与LSTM
PPO通过重要性采样比率裁剪限制策略更新幅度,避免LSTM的隐藏状态剧烈变化:
LCLLP(θ)=E[min(rt(θ)At,clip(rt(θ),1−ε,1+ε)At)]L^{CLLP}(\theta) =\mathbb{E}[\min(r_t(\theta)A_t,clip(r_t(\theta),1-\varepsilon,1+\varepsilon)A_t)]LCLLP(θ)=E[min(rt(θ)At,clip(rt(θ),1−ε,1+ε)At)]
rt(θ)r_t(θ)rt(θ) 是LSTM新旧策略的概率比,裁剪后约束LSTM的参数更新步长。(3)时间序列的梯度传播
LSTM的隐藏状态 h_t 在时间步之间传递,梯度通过 时间反向传播(BPTT) 更新:
- 每个时间步的梯度包含当前奖励和未来奖励的折现(通过γ调节)。
- 序列长度(如8步)影响梯度回溯的深度,需平衡长期记忆和训练稳定性。
四、实验
一旦我们有了训练好的模型,我们就切换到内部模式,在该模式下Unity 3-D环境使用它来导航。Unity将代理的当前状态传递给存储的TensorFlow图,后者返回推荐的动作。这表示在系统当前状态和可能动作集的情况下采取的最佳行动。在内部模式中,不再进行学习,并且模型图被冻结。如果需要,可以通过切换回Unity 3-D设置中的训练模式进一步训练模型。
4.1实验评估: 对比算法

我们比较了三种基于PPO的算法:PPO8和PPO16分别代表带有不同长度8步和16步记忆的LSTM增强版PPO,以及基础的PPO无
记忆。同时,我们还设置了一个启发式算法作为基准对比。启发式算法很简单,就是看哪个方向离目标最近就往哪走,遇到障碍物就随机选个没被挡住的方向。
4.2 实验结果:训练过程分析
图7显示了在训练课程第一课(16x16网格,1个障碍物)的前500万次迭代中PPO、PPO 8和PPO 16的平均奖励以及在训练课程第二课(16x16网格,4个障碍物)期间PPO 8 L2的平均奖励。PPO 8 L2在第一课已经在一个16x16网格上进行了500万次训练迭代,我们展示了这如何影响训练。下图是上图的放大版本,更清楚地显示了平均奖励的波动。类似地,图8示出了PPO、PPO 8和PPO 16的课程的第一课训练期间奖励的标准偏差以及PPO 8的课程的第二课训练期间奖励的标准偏差。
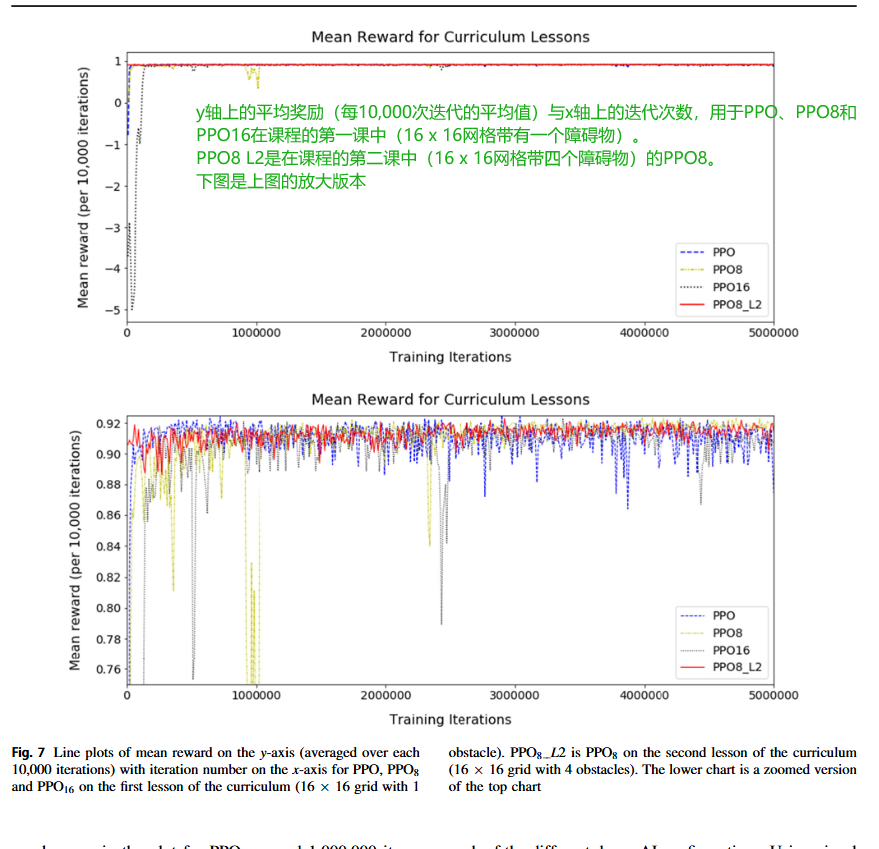
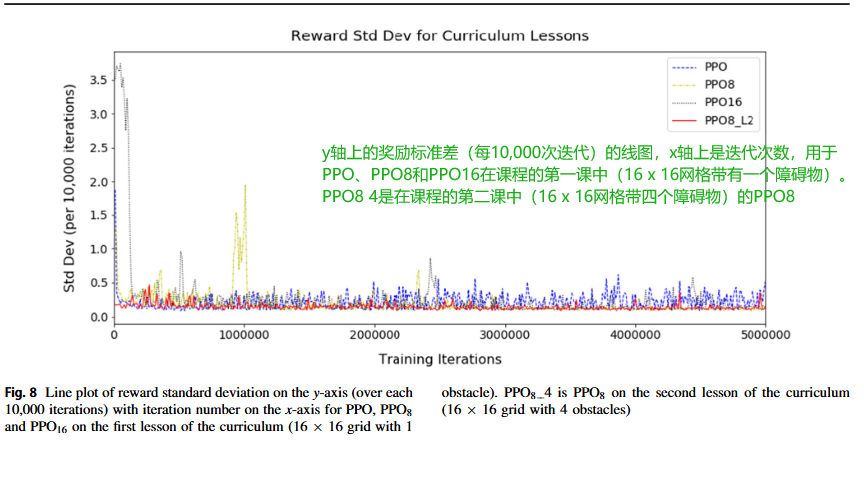
图7和8显示,对于第1课,没有记忆的PPO最初学习最快,因为平均奖励和奖励标准差的曲线波动最小并迅速稳定,但在大约4百万次训练迭代时波动略有增加。图表表明AI的记忆越大,则AI学习所需的时间越长。这通过初始时波动更大且最慢稳定的曲线线来说明。在训练开始时,PPO 16需要240,000次迭代才能达到平均奖励0.9,而PPO和PPO 8则需要50,000和150,000次。然而,在3百万次训练迭代后,由于记忆的帮助,PPO 8的波动最小,与没有记忆的PPO相比。当PPO 8处于第二课时,PPO 8 L2的波动最小,并且迅速稳定下来,因为它已经学会了前一课,并将导航知识从一课传递到下一课。这种长度的可变性表明了为什么我们使用增量课程学习,因为可以根据AI的时间调整每节课的长度,并确保其经过充分训练以学习。图7和图8显示PPO 8和PPO 8 L2已准备好进入下一节,但PPO和PPO 16至少需要额外0.5百万次迭代才能受益。
由于我们的随机网格生成,本课程中标准差存在一些变化。我们计算每块10,000次迭代的平均奖励和奖励标准差。某些区块可能包含更多从起点到目标有长路径的网格,而其他区块可能包含更多有短路径的网格,这是由于偶然性造成的。然而,标准差仍应在一个范围内稳定。在学习过程中,AI有时可能会陷入停滞。这在PPO 8的图表中可以看到,大约在1,000,000次迭代时,平均奖励下降,标准差增加,因为AI需要重新学习。同样,通过改变课程长度并使用度量,我们可以确保AI在进入下一课程之前已经充分学习。

从实验结果来看,PPO8和PPO16在训练初期,也就是刚开始学习的时候,速度确实比没有记忆的PPO要慢一些,曲线波动也更大。这是因为引入LSTM增加了模型的复杂度,学习曲线自然会更陡峭一些。但是,随着训练的进行,特别是当它们积累了足够的经验后,PPO8和PPO16的表现反而更加稳定,而且在处理复杂环境时更有优势。这也再次证明了我们增量课程学习策略的有效性,通过监控奖励指标,我们可以精确控制每个阶段的训练时长,确保模型充分学习后再进入下一阶段,而不是盲目地按预设时间训练。
4.3 实验结果:性能对比
我们分析了场景长度(无人机到达目标所需的步数)、场景结束时的奖励(无论是无人机到达目标、撞到障碍物还是耗尽步数)以及准确度(在2000次运行中,代理成功找到目标的次数)。每个剧集可以持续长达1000步,直到它超时。
图9和表1及2详细说明了每种算法在8个不同网格大小和障碍物数量的网格世界场景中的分析。注意,仅在有32个障碍物的32x32网格上训练了这些代理;所有其他网格世界设置都是新的。
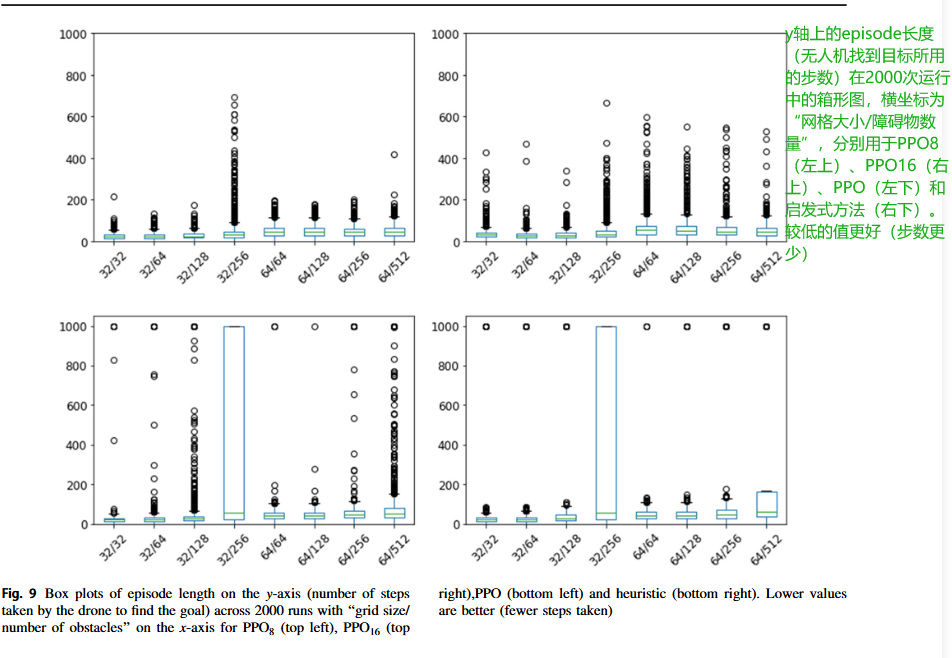

综合来看,PPO8表现最为均衡,可以说是全能选手,在大多数测试场景下都取得了最好的成绩,无论是平均奖励、回合长度还是成功率,都相对较高。PPO16在障碍物非常多、环境极其拥挤的情况下,凭借更强的记忆力,能更好地回溯路径,表现最佳,但代价是训练和运行时间都更长。
五、安全保障
本文中描述的无人机导航推荐系统在现实世界环境中的使用有可能对人类造成伤害。这种伤害可能是由系统直接引起的(例如,系统故障导致无人机与环境中其他障碍物发生碰撞),也可能是由于系统导致无法成功完成任务而间接产生的(例如,延迟紧急救援响应)。如果在现实世界环境中使用无人机导航推荐系统,我们必须提供对系统使用不会导致此类伤害的信心。我们将这种行为安全的自信称为“保证”。本节将重点讨论直接造成的伤害,并简要讨论在系统中证明保证的策略以及部署前需要解决的挑战。
5.1 安全保障:功能失效分析

FFA: 系统地检查系统可能出错的地方。
通过分析这些潜在的故障模式及其可能导致的后果,我们就能识别出哪些是真正需要重点关注的安全风险,并据此制定严格的安
全要求。
5.2 安全保障:训练与模型验证
有了安全要求,接下来就是如何保证满足这些要求。这涉及到三个层面:训练过程的保障、学习模型本身的保障,以及最终系统整体性能的保障。

六、总结与展望

七、模型的实践
7.1 数据收集阶段
- 运行环境:
LSTM基于当前策略控制无人机,生成状态-动作-奖励序列 (s1,a1,r1,...,sTs_1, a_1, r_1, ..., s_Ts1,a1,r1,...,sT)。
- Unity环境生成当前状态 s_t(含障碍物信息、目标相对位置等)。
- LSTM接收 sts_tst 和上一时刻的隐藏状态 ht−1h_{t-1}ht−1,输出动作概率分布 π(at∣st,ht)π(a_t|s_t, h_t)π(at∣st,ht)。
- 按概率采样动作 a_t(如“向东移动”),执行后得到新状态 s_{t+1} 和即时奖励 r_t。
- 隐藏状态 hth_tht 在序列内持续传递,序列间重置。
- 存储经验:将 (st,at,rt,st+1)(s_t, a_t, r_t, s_{t+1})(st,at,rt,st+1)存入经验回放缓冲区,保持时间连续性(LSTM依赖序列顺序)。
7.2 训练阶段
-
采样序列:
从缓冲区抽取多个连续序列(如长度=8 ,(si,ai,ri,si+1)(s_i, a_i, r_i, s_{i+1})(si,ai,ri,si+1) 片段))。
每个序列初始隐藏状态 h_0 可重置为零或继承上一序列末尾状态(实验设定)。 -
LSTM前向传播:
输入序列状态 [s1,s2,...,s8][s_1, s_2, ..., s_8][s1,s2,...,s8],输出对应动作概率 [π1,π2,...,π8][π_1, π_2, ..., π_8][π1,π2,...,π8] 和状态价值 [V1,V2,...,V8][V_1, V_2, ..., V_8][V1,V2,...,V8]。 -
计算优势:
使用广义优势估计(GAE,Generalized Advantage Estimation)计算每个动作的优势值 A_t。 -
损失计算:
联合优化策略损失(含LSTM输出)和值函数损失:
L=LCLIP−c1LVF+c2H(π)L=L^{CLIP} -c_1L^{VF}+c_2 H(\pi)L=LCLIP−c1LVF+c2H(π)
- LVFL^{VF}LVF 是值函数损失(均方误差)。
H(π)是策略熵(鼓励探索)。
- 梯度更新:通过Adam等优化器更新LSTM和全连接层参数
7.3 数据流图示
# 简化的数据流示例
for episode in episodes:h_t = LSTM.init_hidden() # 初始化隐藏状态for t in timesteps:a_t, π_t, V_t = LSTM(s_t, h_t) # 动作采样s_{t+1}, r_t = env.step(a_t) # 环境交互buffer.push(s_t, a_t, r_t, V_t, π_t) # 存储序列h_t = LSTM.update_hidden() # 更新隐藏状态# 训练时
batch = buffer.sample_sequence(length=8)
A_t = GAE.calculate(batch) # 优势估计
loss = PPO_loss(π_t, A_t, V_t) # 计算损失
optimizer.step(loss) # 更新LSTM和策略网络
7.4 优化目标
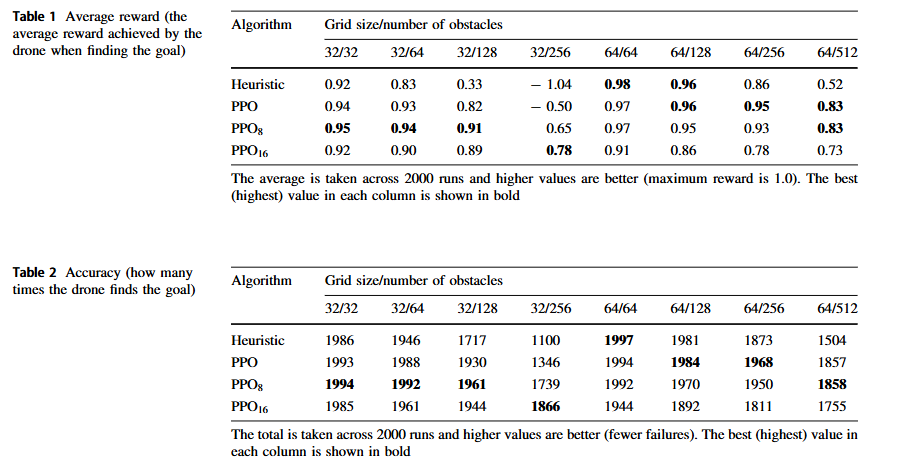
PPO+LSTM的优化目标是最大化期望累积奖励,通过以下两个核心机制实现:
- 策略梯度(Policy Gradient):
- 直接优化策略分布 π(a∣s,h)π(a|s, h)π(a∣s,h),使得高优势动作的概率增加。
- 梯度公式:
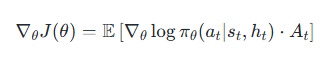
- 值函数优化(Value Function):
- 最小化值函数误差(均方误差),使 V(s_t) 更准确预测累积奖励:
7.6 PPO的约束机制’
-
重要性采样裁剪:限制新旧策略差异,避免LSTM因大幅更新而失效:
LCLIP=E[min(πθ(at∣st,ht)πold(at∣st,ht))At,clip(πθπold,1−ε,1+ε)At]L^{CLIP}=\mathbb{E}[\min(\frac{\pi_{\theta}(a_t|s_t,h_t)}{\pi_{old}(a_t|s_t,h_t)})A_t,clip(\frac{\pi_{\theta}}{\pi_{old}},1-\varepsilon, 1+\varepsilon)A_t]LCLIP=E[min(πold(at∣st,ht)πθ(at∣st,ht))At,clip(πoldπθ,1−ε,1+ε)At] -
熵正则化:鼓励探索,防止策略过早收敛:
-
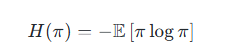
7.7 LSTM的时序优化
- 时间反向传播(BPTT) :梯度沿时间步传播,更新LSTM的权重和隐藏状态。
- 序列长度权衡:
过短(如4步):无法学习长期依赖(如绕行U型障碍)。
过长(如16步):梯度消失/爆炸风险增加(论文中选择8步)。
7.8 LSTM+PPO的网络结构
(1) 共享的LSTM主干
输入层:接收当前状态 s_t 和上一时刻的隐藏状态 h_{t-1}。
- 状态 s_t 的维度:[N, E, S, W障碍信息, x-distance, y-distance](6维向量)。
- 示例:[0, 1, 0, 0, 3.2, -1.5] 表示东侧有障碍,目标在东北方向。
- 训练时输入一个时间窗口的序列(如长度=8),形状为 [batch_size, 8, 6]。
LSTM层:
- 隐藏单元数:64(论文附录超参数)。
- 层数:1层(单层LSTM已足够处理导航任务的时序依赖)。
- 输出:时序特征 h_t(隐藏状态)和 c_t(细胞状态)。
(2) 分离的输出头
策略头(Policy Head):
- 结构:全连接层(Linear + Softmax)。
- 输入:LSTM输出的 h_t。
- 输出:动作概率分布 π(a|s_t)(4维,对应 N, E, S, W)。如 [N:0.7, E:0.1, S:0.1, W:0.1]。
价值头(Value Head):
- 结构:全连接层(Linear)。
- 输入:与策略头共享 h_t。
- 输出:标量状态价值 V(s_t)(预测当前状态的长期回报)。标量,如 0.85,表示当前状态的预期累积奖励。
(3)结构代码示例
# 伪代码描述网络结构
class PPOLSTM(nn.Module):def __init__(self):self.lstm = nn.LSTM(input_size=6, hidden_size=64, num_layers=1)self.policy_head = nn.Sequential(nn.Linear(64, 4), # 4 actionsnn.Softmax(dim=-1))self.value_head = nn.Linear(64, 1) # 1 valuedef forward(self, s_t, h_t):# s_t: [batch_size, sequence_length, 6]# h_t: (h0, c0) 两个张量形状都是 [num_layers, batch_size, hidden_size]lstm_out, (h_next, c_next) = self.lstm(s_t, h_t)# lstm_out: [batch_size, seq_len, 64]policy = self.policy_head(lstm_out) # [batch, seq_len, 4]value = self.value_head(lstm_out) # [batch, seq_len, 1]return policy, value, (h_next, c_next)

| 变量 | 形状 | 含义 |
|---|---|---|
s_t | [B, L, 6] | 一批长度为 L 的序列观测(可一次送 L=1 做单步,也可 L=T 做整段 rollout)。 |
h_t | 元组 (h0, c0) | LSTM 的初始/当前隐状态,形状 [1, B, 64]。推理时要记得把上一时刻的 (h_next, c_next) 传回来。 |
lstm_out | [B, L, 64] | 所有时间步的隐状态序列。 |
policy | [B, L, 4] | 每一步每个动作的 softmax 概率。 |
value | [B, L, 1] | 每一步的状态值 V(s)。 |
(h_next, c_next) | [1, B, 64] | 经过 L 步后的最终隐状态,用于下一步继续 rollout 或训练。 |
(4)数据收集
h = (torch.zeros(1, B, 64), torch.zeros(1, B, 64)) # 初始化 LSTM 隐藏态
for t in range(T):obs = env.step(...) # [B, 6]logits, val, h = model(obs.unsqueeze(1), h) # unsqueeze 变成 [B,1,6]action = Categorical(logits.squeeze(1)).sample()buffer.store(obs, action, val.squeeze(), h_old=h)
7.9 策略网络与价值网络的关系
(1) 参数共享
- 共享LSTM:策略和价值头共用同一LSTM提取的时序特征,减少计算量并提升稳定性。
- 分离梯度:策略头和价值头的梯度独立回传,但LSTM的梯度是两者的加权和
(2) 联合优化目标
总损失函数结合策略损失、值函数损失和熵正则化:
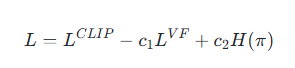
- LCLIPL^{CLIP}LCLIP:PPO的策略裁剪损失(基于动作概率和优势值)。
- LVFL^{VF}LVF:值函数的均方误差损失 (V(s_t) - R_t)^2。
- H(π)H(π)H(π):策略熵(鼓励探索),通过策略头的Softmax输出计算。
(3)若策略网络和价值网络完全独立(非共享LSTM):
- 优点:避免任务冲突(如价值拟合可能干扰策略学习)。
- 缺点:
参数翻倍,训练更慢。
时序特征需分别学习,效率低。
论文选择:共享LSTM更适合样本效率要求高的强化学习任务。

