嵌入式下快速傅里叶变换(FFT)C语言库kissfft
一.FFT常用库(C/C++)
1.FFTW
(1)最常用的当属FFTW(Fastest Fourier Transform in the West),FFTW是一个专注于快速傅里叶变换(FFT)的高性能计算库,被广泛应用于科学计算、信号处理、图像处理等领域。
(2)跨平台兼容:
支持 Linux、Windows、macOS 等主流操作系统,以及 x86、ARM、PowerPC 等处理器架构。
可无缝集成到 Python(通过 SciPy)、MATLAB、R 等高级语言中。
(3)FFTW比较通用,由于之前写过两篇相关文章,本文不做重点阐述。
<<QT实现FFT整体流程及结果展示>>
<<FFTW库在vs2022下编译lib库及在QT6.8中调用>>
2.KissFFT(本文重点介绍)
(1)KissFFT(Keep It Simple, Stupid Fast Fourier Transform)是一个轻量级、高性能的 FFT 库,其核心优势在于代码简洁(约 500 行)、无外部依赖、支持定点/浮点运算,特别适合嵌入式系统和实时处理场景。
官网:https://github.com/mborgerding/kissfft
(2)核心特性

二.KissFFT使用
1.浮点输入模式(默认)
头文件配置:无特殊定义
数据类型:
typedef float kiss_fft_scalar; // 实数输入类型
typedef struct { float r; float i; } kiss_fft_cpx; // 复数类型
适用场景:PC、服务器、带FPU的嵌入式设备
2.整型输入模式(定点数)
头文件配置(在 kiss_fft.h 中定义):
#define FIXED_POINT 16 // 16位定点 (Q15)
// 或
#define FIXED_POINT 32 // 32位定点 (Q31)
数据类型:
typedef int16_t kiss_fft_scalar; // Q15 输入
typedef struct { int16_t r; int16_t i; } kiss_fft_cpx;
Q格式说明:
Q15:数值范围 [-1.0, 1.0) 映射到 [-32768, 32767]
计算时需手动缩放(如 input = raw_data >> 4)
3.代码示例:浮点数 FFT(1024 点)
#include "kiss_fft.h"
void float_fft_example() {
const int N = 1024;
kiss_fft_cfg cfg = kiss_fft_alloc(N, 0, NULL, NULL); // 正向FFT
// 准备输入(实数信号)
kiss_fft_scalar in[N];
for (int i = 0; i < N; i++) {
in[i] = sinf(2 * M_PI * 100 * i / 44100.0f); // 100Hz正弦波
}
// 执行实数FFT(需 kiss_fftr.h)
kiss_fft_cpx out[N/2 + 1];
kiss_fftr_cfg rcfg = kiss_fftr_alloc(N, 0, NULL, NULL);
kiss_fftr(rcfg, in, out); // 实数FFT计算
// 计算幅度谱
float mag[N/2 + 1];
for (int i = 0; i <= N/2; i++) {
mag[i] = sqrtf(out[i].r * out[i].r + out[i].i * out[i].i);
}
// 释放资源
kiss_fft_free(cfg);
kiss_fftr_free(rcfg);
}
4.代码示例:整型输入 FFT(Q15 定点数)
#define FIXED_POINT 16 // 启用16位定点模式
#include "kiss_fftr.h"
void fixed_point_fft_example() {
const int N = 512;
const int SCALE_SHIFT = 3; // 缩放因子(防溢出)
// 配置FFT(正向实数变换)
kiss_fftr_cfg cfg = kiss_fftr_alloc(N, 0, NULL, NULL);
// 准备整型输入(Q15格式)
kiss_fft_scalar in[N]; // 实际类型为 int16_t
int16_t adc_data[N] = {...}; // 原始ADC数据(-32768~32767)
// 缩放至Q15范围 [-1.0, 1.0)
for (int i = 0; i < N; i++) {
in[i] = adc_data[i] >> SCALE_SHIFT; // 防溢出缩放
}
// 执行FFT
kiss_fft_cpx out[N/2 + 1];
kiss_fftr(cfg, in, out);
// 计算幅度(需反缩放)
int32_t mag[N/2 + 1];
const int32_t scale_correction = 1 << (SCALE_SHIFT + 1); // 补偿因子
for (int i = 0; i <= N/2; i++) {
int32_t re = (int32_t)out[i].r * scale_correction;
int32_t im = (int32_t)out[i].i * scale_correction;
mag[i] = sqrt(re * re + im * im); // 实际需用查表法优化
}
kiss_fftr_free(cfg);
}
5.总结
浮点模式:精度高(~1e-6),适合科学计算
定点模式:速度快、功耗低,适合实时嵌入式系统
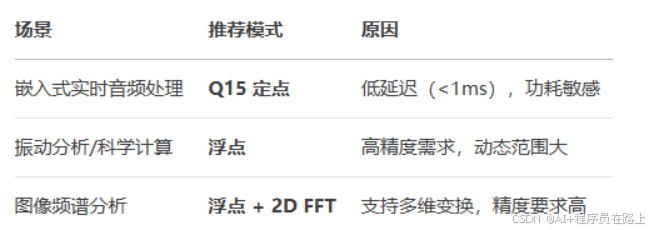
6.选择建议