【深度学习】神经网络-part3

五、参数初始化

初始化参数（通常是权重和偏置）会对模型的训练速度、收敛性以及最终的性能产生重要影响。

1.固定值初始化

将所有权重或偏置初始化为一个特定的常数值。这种初始化方法虽然简单，但在实际深度学习应用中通常并不推荐。

1.1 全零初始化

所有权重参数初始化为0

缺点：对称性破坏 ，每个神经元都在每一层中执行相同的计算 模型不能学习

应用场景 ： 通常不初始化权重 但用来初始化偏置

对称性问题：

现象：同一层神经元都又完全相同的初始权重和偏置

后果：
反向传播时候， 所有神经元都会收到相同的梯度，导致权重更新完全一致

无论训练多久，同一层神经元本质保持相同的功能（相当于“一个神经元”的多个副本） ，模型表达能力极大降低

代码：

import torch
import torch.nn as nn
def func():# 全0参数初始化linear = nn.Linear(in_features=6,out_features=4)# 处死话权重参数nn.init.zeros_(linear.weight)# 打印权重参数print(linear.weight)
func()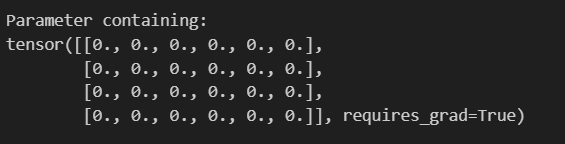

 1.2 全1初始化

每个神经元接收导相同的输入信息，进而输出相同的值，会导致模型无法收敛，全1初始化至少一个理论化的初始化方法，实际不适用

代码：

def func1():# 全1初始化linear = nn.Linear(6,4)# 初始化权重参数nn.init.ones_(linear.weight)print(linear.weight)
func1()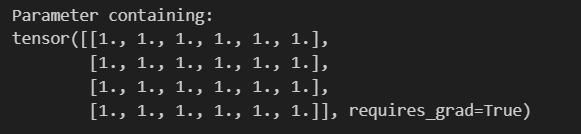

1.3 任意常数的初始化

所有参数初始化为非0的常数，虽然 不同全0或1，但仍然不能避免对称性破坏的问题

def func2():# 全1初始化linear = nn.Linear(6,4)# 初始化权重参数nn.init.constant_(linear.weight,.77)print(linear.weight)
func2()

def func3():net = nn.Linear(2,2,bias=True)# 假设数值x = torch.tensor([[0.1,0.95]])# 初始化权重参数net.weight.data = torch.tensor([[0.1,0.2],[0.3,0.4]])# 输出:权重参数会转置output = net(x)print(output,net.bias)pass
func3()

所有输入特征被同等对待 无法学习特征间的不同重要性

2.随机初始化

方法：随机小值，通常从正态分布或均匀分布中采样

应用场景：最基本的初始化方法，通过随机初始化的方法来避免对称性破坏

 随机分布均匀初始化

linear = nn.Linear(6,4)
nn.init.uniform_(linear.weight)
print(linear.weight)

 正太分布初始化

linear = nn.Linear(6,4)
nn.init.normal_(linear.weight)
print(linear.weight)

 3.Xavier初始化

前置知识

均匀分布

函数 

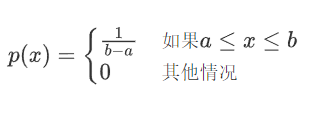
计算期望值（均值）：

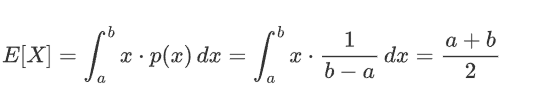
计算方差（二阶矩减去均值的平方）：

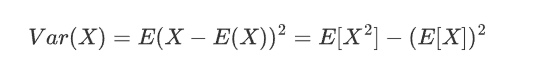
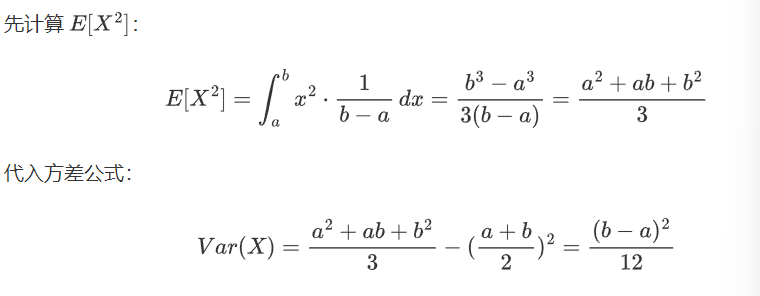
Xvaier初始化是一种自适应权重初始化方法 ，专门为解决神经网络训练初期的梯度消失或爆炸问题而设计。Xavier 初始化也叫做Glorot初始化。Xavier 初始化的核心思想是根据输入和输出的维度来初始化权重，使得每一层的输出的方差保持一致。具体来说，权重的初始化范围取决于前一层的神经元数量（输入维度）和当前层的神经元数量（输出维度）。

方法：根据输入和输出神经元的数量来选择权重的初始值。

（1）向前传播的方差一致性

（2）反向传播的梯度方差一致性

（3）综合考虑

优点：平衡了输入和输出的方差 适合Sigmod和Tanh激活函数

应用场景：常用于浅层网络或使用Sigmod，Tanh激活函数网络

linear = nn.Linear(6,4)
# 正态分布
nn.init.xavier_normal_(linear.weight)
print(f"正态分布：{linear.weight}")
# 均匀分布
linear = nn.Linear(6,4)
nn.init.xavier_uniform_(linear.weight)
print(f"均匀分布：{linear.weight}")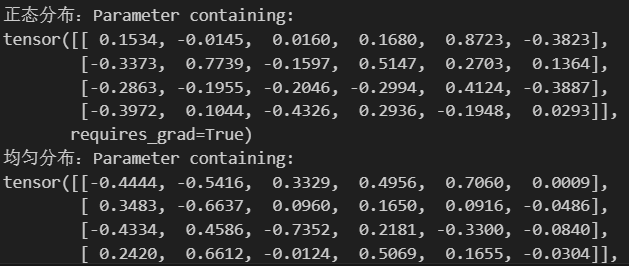

 4.He初始化

也叫kaiming。核心思想：调整权重的初始化范围，使得每一层的输出的方差保持一致。He专门正对ReLU激活函数的特征进行了优化

（1）向前传播的方差一致性

（2）反向传播的梯度一致性

（3）两种模式

优点：使用ReLU和LeakyReLU激活函数

场景应用：深度网络，尤其是ReLU激活函数

linear = nn.Linear(6,4)
# 正态分布
nn.init.kaiming_normal_(linear.weight,nonlinearity="relu",mode = "fan_in")
print(linear.weight)
# 均匀分布
nn.init.kaiming_uniform_(linear.weight,nonlinearity="relu",mode = "fan_out")
print(linear.weight)

5. 总结

在使用Torch构建网络模型时，每个网络层的参数都有默认的初始化方法，同时还可以通过以上方法来对网络参数进行初始化。

六、损失函数

1.线性回归损失函数

1.1 MAE损失

平均绝对误差 通常也被称为L1-Loss ,通常对预测值和真实值之间的绝对差取平均值来平滑他们之间的差异

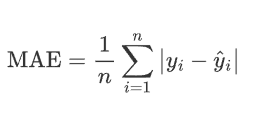
其中：

n 是样本的总数。

是第 i 个样本的真实值。

是第 i 个样本的预测值。

是真实值和预测值之间的绝对误差。

特点：

鲁棒性：不会像MSE那样对较大的误差平方敏感

物理意义直观：于原始数据相同的单位度量误差，易于解释

应用场景：需要对误差进行线性度量的情况，尤其是数据在可能存在异常值的时候，避免对异常值进行过度的惩罚

# 初始化损失函数
mae_loss = nn.L1Loss()
y_true = torch.tensor([2,5,2.5])
y_pred = torch.tensor([2.5,5,3])
# 计算MAE
loss = mae_loss(y_pred,y_true)
print(f"MAE Loss:{loss.item()}")

1.2 MES损失

均方差损失，也叫L2Loss

通过对预测值和真实值之间的误差平方取均值，来预测测试值与真实值之间的差异

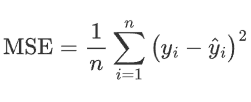
特点：对误差的惩罚更加严重，对异常值异常敏感

凸性：意味着它是一个具有唯一的全家最小值，有助于优化问题的求解

应用场景：

被广泛应用于神经网络中

mes_loss = nn.MSELoss()
y_true = torch.tensor([3,5,2.5])
y_pred = torch.tensor([2.5,5,3])loss = mes_loss(y_pred,y_true)
print(f"MES LOSS:{loss.item()}")

2.CrossEntropyLoss

2.1信息量

用于衡量一个事件包含的信息多少，定义：事件发生的概率越低，信息量越大

 对于一个事件x，其发生的概率为 P(x)，信息量I(x) 定义为：

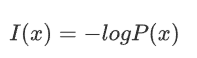
形状：

非负性 ： I(x)≥0。

单调性 ： P(x)越小，I(x)越大

2.2 信息熵

信息熵是信息量的期望值，熵越高，表示随机变量的不确定性越大，反之同理

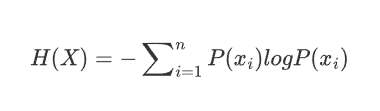
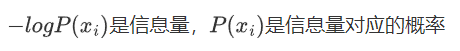
2.3 KL散度

横量两个概率分布之间的差异，用一个分布Q来近似另一个分布P时，损失的信息量，KL散度越小，分布越近

 

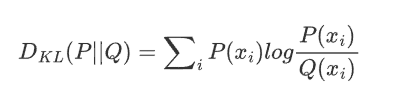
P 是真实分布，Q是近似分布。

2.4 交叉熵

KL散度公式展开：

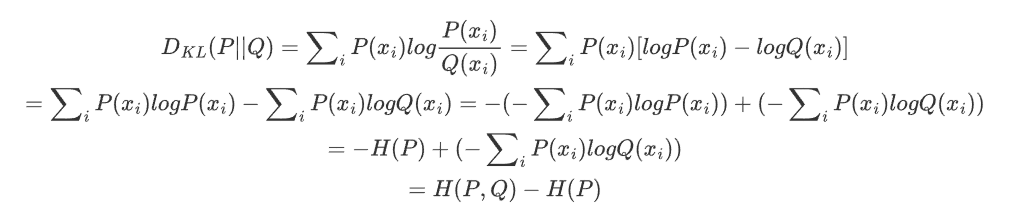
P是真实分布，H(P)是常数，所以KL散度可以用H(P,Q)来表示；H(P,Q)叫做交叉熵。

如果将P换成y，Q换成\hat{y},则交叉熵公式为：

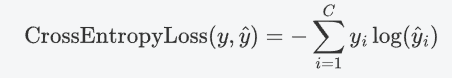
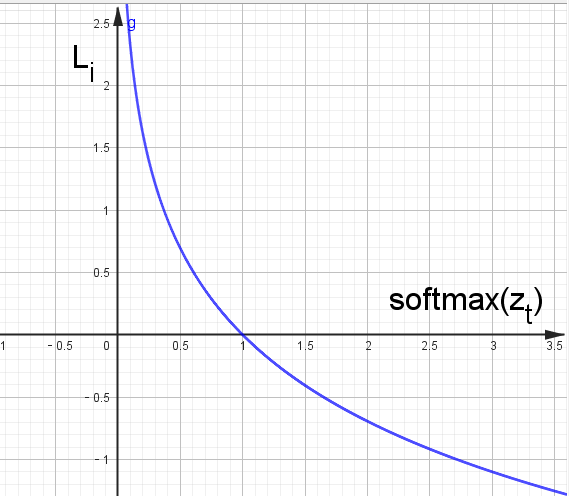
特点：

        概率输出：CrossEntroyLoss通常与softmax函数一起用，使得模型的输出为一个概率分布（和为1）。nn.CrossEntropyLoss已经内置了softmax操作，如果在输出层显示的添加softmax，会导致重复应用，影响模型的训练。

        惩罚错误分类：该损失函数在真实类别的预测概率较低时候，会实施较大的惩罚，更加注重正确类别的预测概率

        多分类问题的标准选择：多分类问题CrossEntropyLoss时首选的损失函数

应用场景：

分类问题包括图像分类，文本分类，尤其是神经网络中

交叉熵公式 

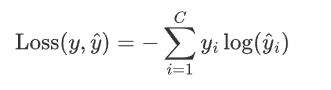
因为y_i是one-hot编码，其值不是1便是0，又是乘法，所以只要知道1对应的index就可以了，展开后：

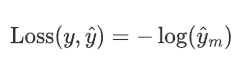
其中，m表示真实类别。

因为神经网络最后一层分类总是接softmax，所以可以把\hat{y}_m直接看为是softmax后的结果。

 

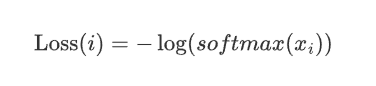
所以，CrossEntropyLoss 实质上是两步的组合：Cross Entropy = Log-Softmax + NLLLoss  

• Log-Softmax：对输入 logits 先计算对数 softmax：log(softmax(x))。

• NLLLoss（Negative Log-Likelihood）：对 log-softmax 的结果计算负对数似然损失。简单理解就是求负数。原因是概率值通常在 0 到 1 之间，取对数后会变成负数。为了使损失值为正数，需要取负数。

对于softmax(x_i)，在softmax介绍中了解到，需要减去最大值以确保数值稳定。

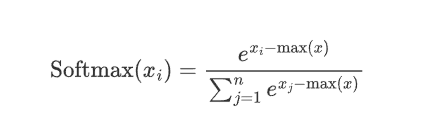
则：

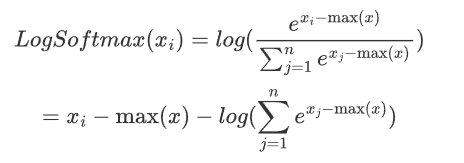
所以：

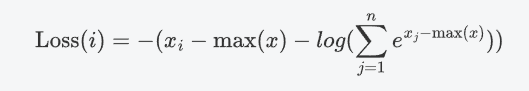
总的交叉熵损失函数是所有样本的平均值：

import torch
import torch.nn as nnlogits = torch.tensor([[1.5,2,0.5],[0.5,1.0,1.5]])
labels = torch.tensor([1,2])criterion = nn.CrossEntropyLoss()
loss = criterion(logits,labels)
print(F"cross Entropy Loss:{loss.item()}")

分析：

LogSoftmax操作

对每个样本进行LogSoftmax函数操作：公式

对于第一个样本 [1.5, 2.0, 0.5]：

减去最大值

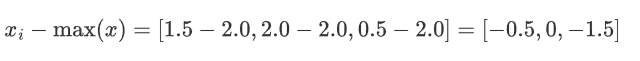
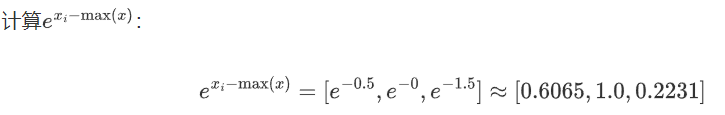
 求和并取对数

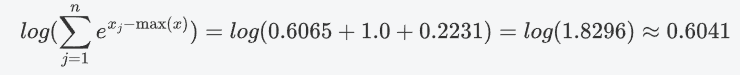
计算Log_Softmax:

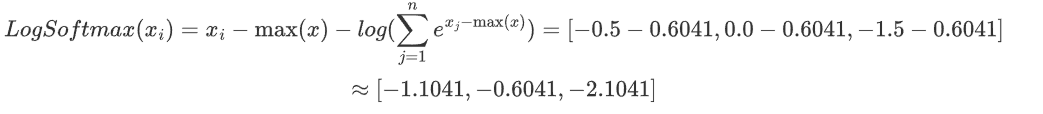
样本二同理

计算每个样本的损失

根据真实标签zt计算每个样本的交叉熵损失

对于这两个样本真实类别是1 ，对应的softmax值是-0.6041；2是-0.6803

计算平均损失

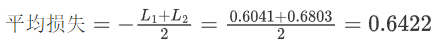
3.BCELoss

二分类交叉熵损失函数，使用在输出层使用sigmod函数进行二分类时

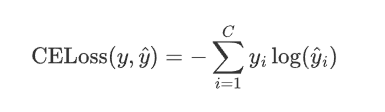
二分类问题 真实标签y的值为0或1，假设模型预测为正类的概率为，则

所以

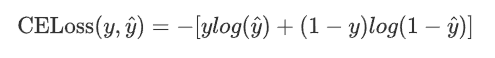
y = torch.tensor([[0.7],[0.2],[0.9],[0.7]])
t = torch.tensor([[1],[0],[1],[0]],dtype=torch.float32)bceLoss = nn.BCELoss()
loss1 = bceLoss(y,t)loss2 = nn.functional.binary_cross_entropy(y,t)print(loss1,loss2)

 

样本	y_i	t_i	计算项 t_i * log(y_i) + (1-t_i) * log(1-y_i)
1	0.7	1	1*log(0.7) + 0*log(0.3) ≈ -0.3567
2	0.2	0	0*log(0.2) + 1*log(0.8) ≈ -0.2231
3	0.9	1	1*log(0.9) + 0*log(0.1) ≈ -0.1054
4	0.7	0	0*log(0.7) + 1*log(0.3) ≈ -1.2040

 

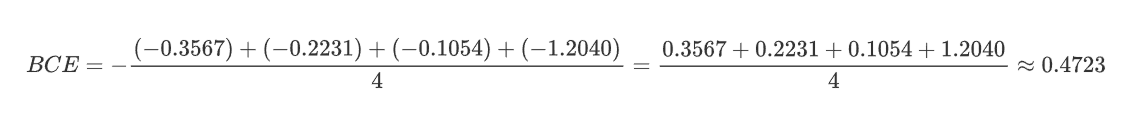
 4.总结

1、当输出层使用softmax多分类时，使用交叉熵损失函数

当输出层使用sigmod二分类时，使用二分类交叉熵损失函数，比如在逻辑回归中使用

当功能为线性回归的时候 使用均方差损失 L2 loss