数据降维方法:PCA
数据降维方法
文章目录
- 数据降维方法
- PCA
- PCA算法
- 代码展示
PCA
**主成分分析(Principal Component Analysis,PCA)**是一种常用的数据降维方法。它通过线性变换将原始数据变换到一个新的坐标系中,使得第一个坐标(第一主成分)具有最大的方差,第二个坐标(第二主成分)具有次大的方差,以此类推。PCA的目的是从高维数据中提取出最重要的特征,通过保留最重要的主成分来实现数据的降维,同时尽可能保留原始数据的结构。
PCA算法
- 数据标准化
为了消除不同特征之间的量纲影响,通常需要对数据进行标准化处理,使得每个特征的均值为0,标准差为1。
标准化公式:
x′=x−μσ,x' = \frac{x - \mu}{\sigma},x′=σx−μ,
其中μ\muμ为特征均值,σ\sigmaσ为特征标准差。
- 计算协方差矩阵
协方差矩阵描述了数据特征之间的相关性。对于标准化后的数据,协方差矩阵可以通过计算特征之间的协方差得到。
协方差公式:
cov(X,Y)=1n−1∑i=1n(Xi−μX)(Yi−μY),cov(X,Y) = \frac{1}{n-1}\sum_{i=1}^{n}(X_i - \mu_X)(Y_i - \mu_Y),cov(X,Y)=n−11i=1∑n(Xi−μX)(Yi−μY),
标准化后简化为特征向量的内积平均。
- 计算特征值和特征向量
求解协方差矩阵的特征值和对应的特征向量。特征值表示对应特征向量方向上的数据方差大小,特征向量给出了数据的主要分布方向(即主成分)。
- 选择主成分
根据特征值的大小,选择前kkk个最大的特征值对应的特征向量,这些特征向量构成了新的kkk维特征空间。特征值的累计贡献率(如前kkk个特征值之和占总特征值之和的比例)通常作为选择kkk的依据(如累计贡献率≥85%)。
- 变换数据
将原始数据投影到新的特征空间中,得到降维后的数据。投影过程通过原始数据矩阵与选定的特征向量矩阵相乘实现。
代码展示
import pandas as pd
from sklearn import datasets# 加载鸢尾花数据集
iris = datasets.load_iris()# 将数据集转换为DataFrame
iris_df = pd.DataFrame(data=iris.data, # 特征数据columns=iris.feature_names # 特征名称
)iris_df.info()iris.data_std = (iris.data - iris.data.mean(axis=0)) / iris.data.std(axis=0)from sklearn.decomposition import PCA# 设置PCA参数,这里我们选择保留90%的方差
pca = PCA(n_components=0.9)
iris.data_pca = pca.fit_transform(iris.data_std)# 可视化原始数据和降维后的数据
import matplotlib.pyplot as pltplt.figure(figsize=(12, 6))
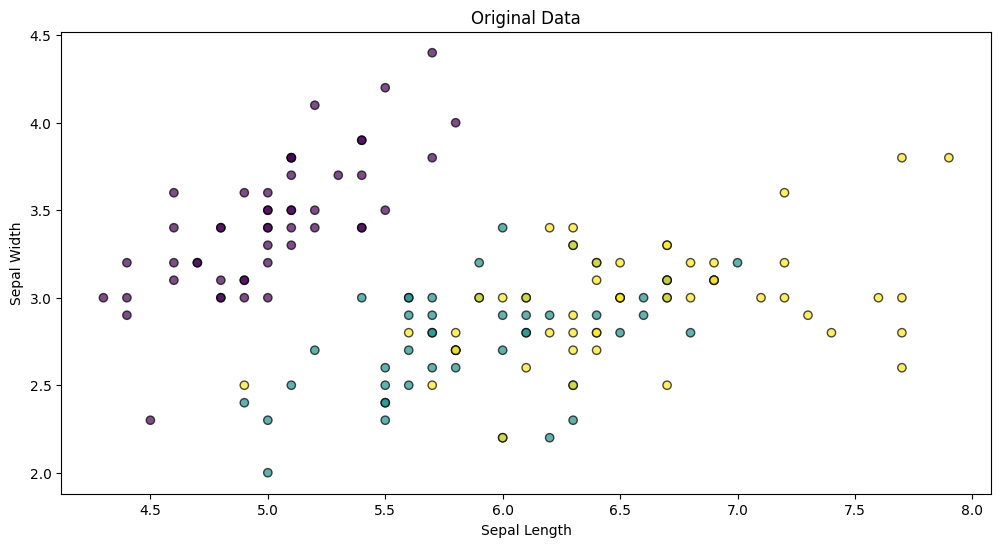
plt.scatter(iris.data[:, 0], iris.data[:, 1], c=iris.target, edgecolor='k', alpha=0.7)
plt.xlabel('Sepal Length')
plt.ylabel('Sepal Width')
plt.title('Original Data')
plt.show()plt.figure(figsize=(12, 6));
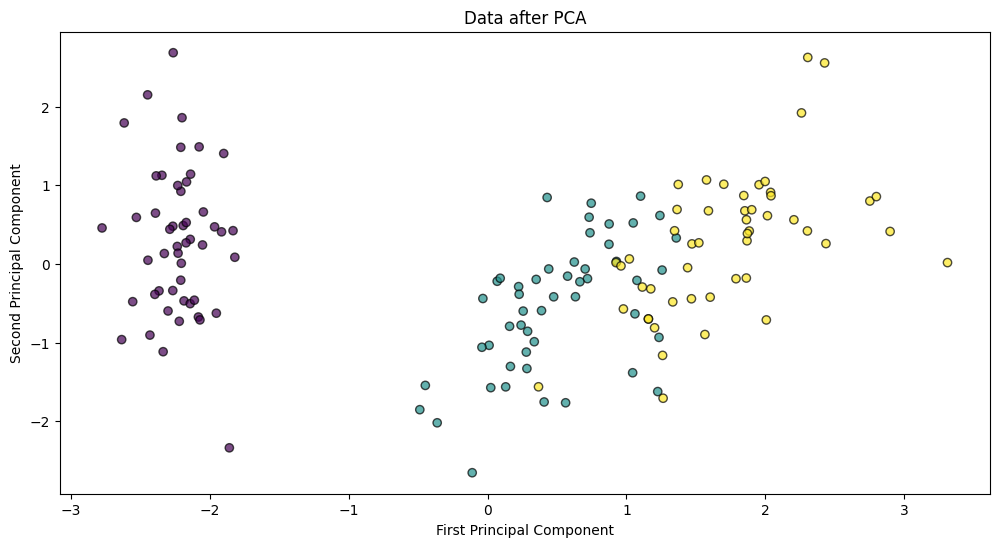
plt.scatter(iris.data_pca[:, 0], iris.data_pca[:, 1], c=iris.target, edgecolor='k', alpha=0.7)
plt.xlabel('First Principal Component')
plt.ylabel('Second Principal Component')
plt.title('Data after PCA')
plt.show()