LeetCode Hot100【4. 寻找两个正序数组的中位数】

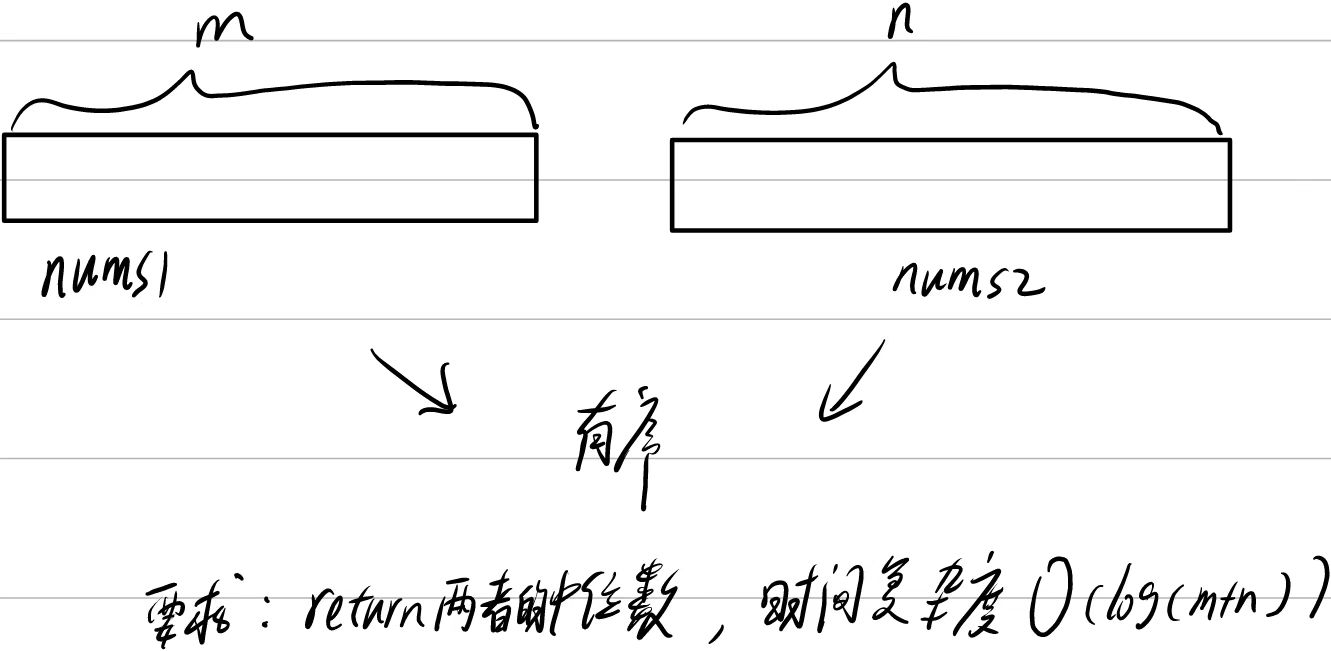
4. 寻找两个正序数组的中位数

自己做 

分析

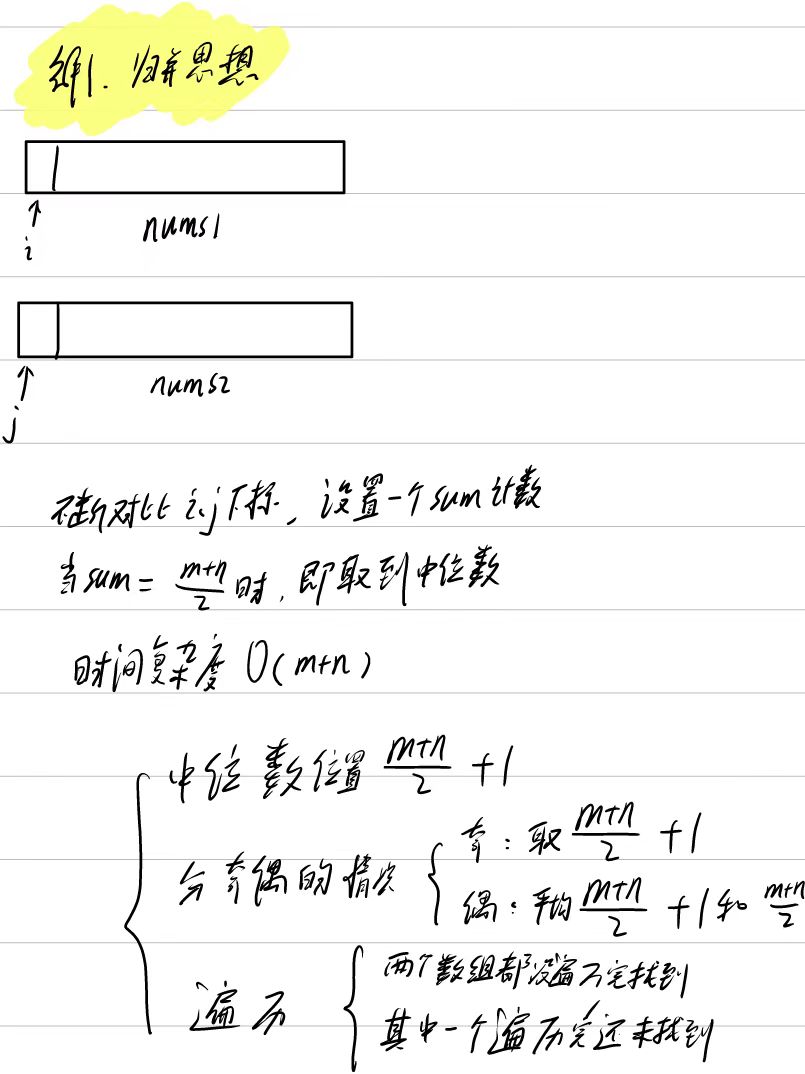
解1：归并思想

class Solution {
public:double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {int sum = 0;double value;queue<double> value2;int i = 0, j = 0;if ((nums1.size() + nums2.size()) % 2 == 1) {                 //两数组大小相加为奇数【只有一个中位数】while (i < nums1.size() && j < nums2.size()) {if (nums1[i] < nums2[j]) {value = nums1[i];           //相当于取nums1[i]i++;}else {value = nums2[j];           //相当于取nums2[j]j++;}sum++;if (sum == (nums1.size() + nums2.size()) / 2 + 1)        //找到中位数return value;}while (i < nums1.size()) {        //遍历完其中一个数组还没有找到value = nums1[i];           //相当于取nums1[i]i++;sum++;if (sum == (nums1.size() + nums2.size()) / 2 + 1)        //找到中位数return value;}while (j < nums2.size()) {        //遍历完其中一个数组还没有找到value = nums2[j];           //相当于取nums2[j]j++;sum++;if (sum == (nums1.size() + nums2.size()) / 2 + 1)        //找到中位数return value;}}else {                               //两数组大小相加为偶数【需要合并】while (i < nums1.size() && j < nums2.size()) {if (nums1[i] < nums2[j]) {value2.push(nums1[i]);           //相当于取nums1[i]i++;if (value2.size() > 2)             //只维护两个数据value2.pop();}else{value2.push(nums2[j]);           //相当于取nums2[j]j++;if (value2.size() > 2)             //只维护两个数据value2.pop();}sum++;if (sum == (nums1.size() + nums2.size()) / 2 + 1) {        //找到中位数double num1 = value2.back();double num2 = value2.front();value = (num1 + num2) / 2;return value;}}while (i < nums1.size()) {        //遍历完其中一个数组还没有找到value2.push(nums1[i]);           //相当于取nums1[i]i++;if (value2.size() > 2)             //只维护两个数据value2.pop();sum++;if (sum == (nums1.size() + nums2.size()) / 2 + 1) {        //找到中位数double num1 = value2.back();double num2 = value2.front();value = (num1 + num2) / 2;return value;}}while (j < nums2.size()) {        //遍历完其中一个数组还没有找到value2.push(nums2[j]);           //相当于取nums2[j]j++;if (value2.size() > 2)             //只维护两个数据value2.pop();sum++;if (sum == (nums1.size() + nums2.size()) / 2 + 1) {        //找到中位数double num1 = value2.back();double num2 = value2.front();value = (num1 + num2) / 2;return value;}}}return 0;}
};

思考

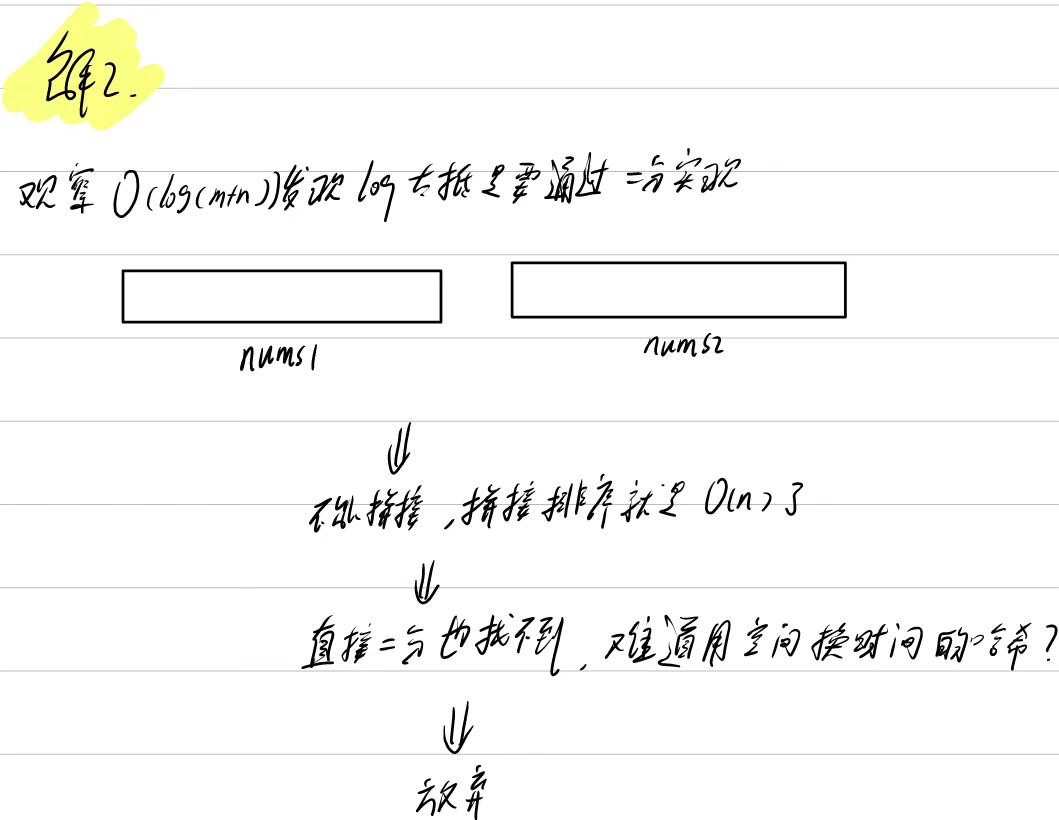
看题解【想不到】

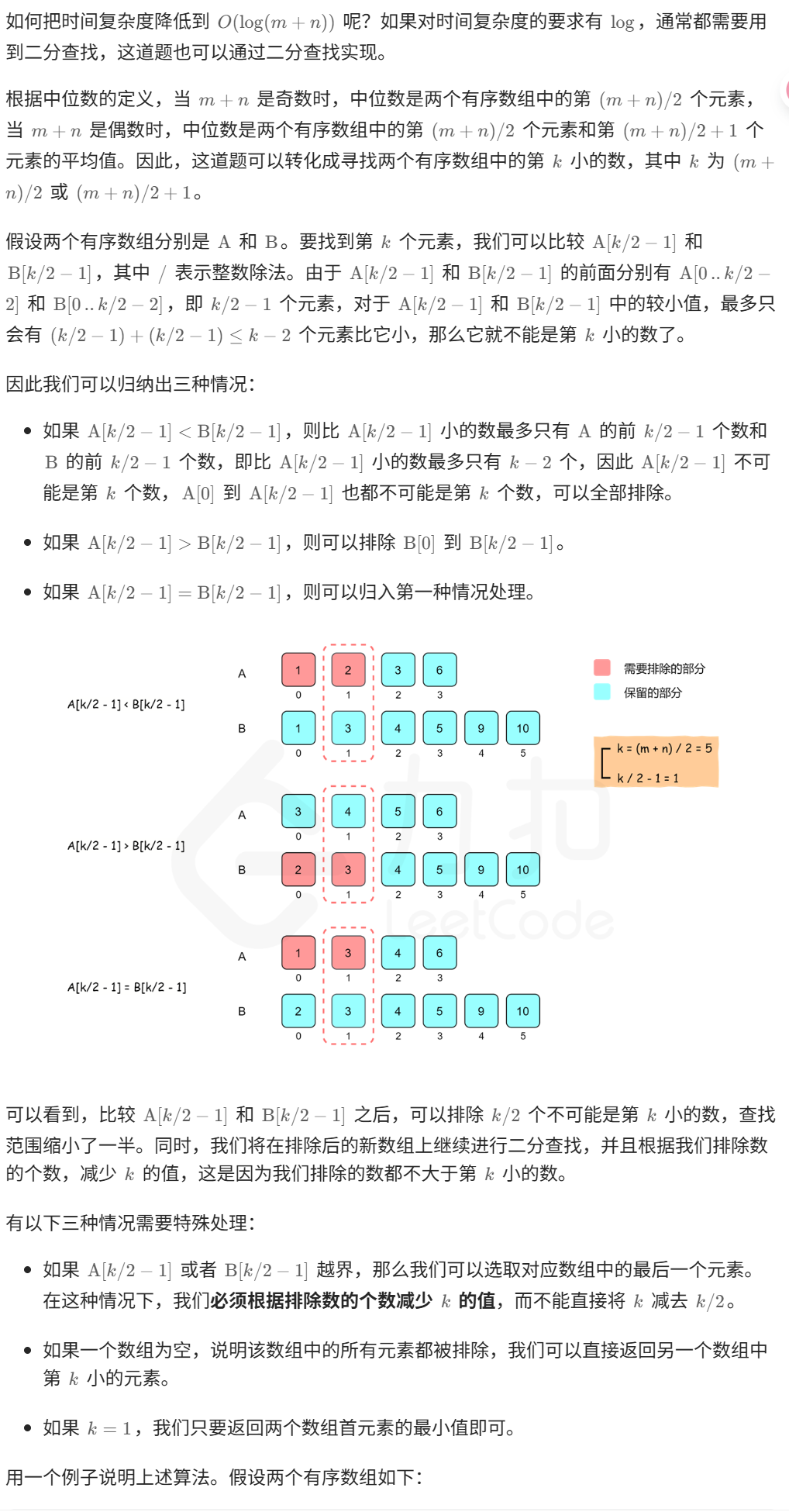
总结：使用二分我们可以直接排除不可能是中位数的数

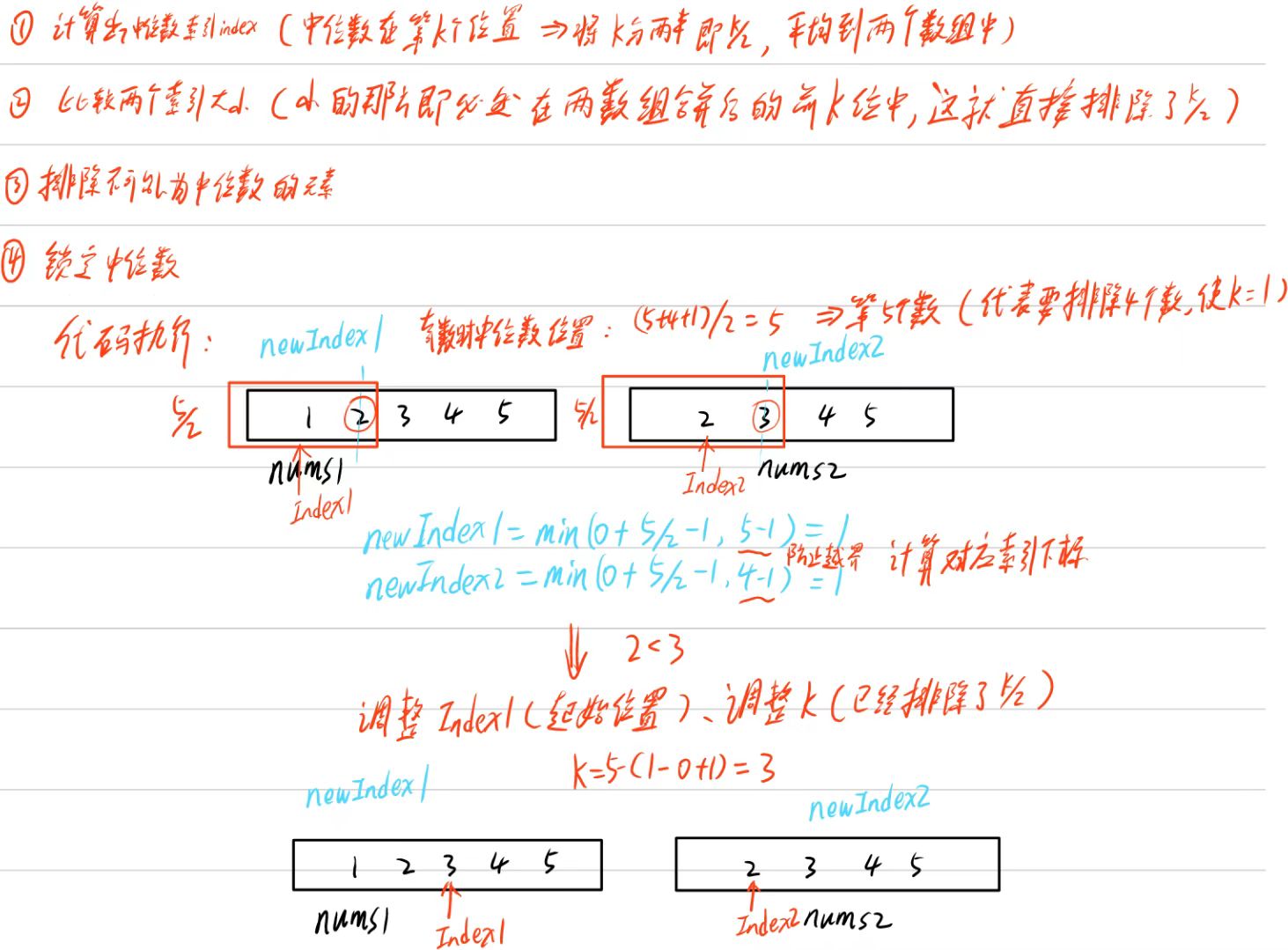
仿写

class Solution {
public:int getKthElement(const vector<int>& nums1, const vector <int>& nums2, int k) {     //寻找中位数（位置为k）对应元素int index1 = 0, index2 = 0;         //两数组的中位索引int len1 = nums1.size();            //注：nums1.size()返回的是无符号整型，这一步就是为了将无符号整型转化为有符号int len2 = nums2.size();while(true) {if(index1 == len1)          //nums1为空数组return nums2[index2 + k - 1];   //直接返回nums2的第k个元素【即Nums2的中位数就是两者合并的中位数】if (index2 == len2)          //nums2为空数组return nums1[index1 + k - 1];   //直接返回nums1的第k个元素【即Nums1的中位数就是两者合并的中位数】if (k == 1) {                //将中位数前面的数全部排除后，k = 1，这个数即是中位数return min(nums1[index1], nums2[index2]);   //排除的过程中，会不断移动Index，当k=1时即只剩下了中位数，这种情况下就代表了前k-1个数已经完全排除了，第k个数即为中位数，也是剩余数中最小的}//正常情况，平分k/2int newIndex1 = min(index1 + k / 2 - 1, len1 - 1);          //偏移中轴位置int newIndex2 = min(index2 + k / 2 - 1, len2 - 1);          //偏移中轴位置int pivot1 = nums1[newIndex1];int pivot2 = nums2[newIndex2];if (pivot1 <= pivot2) {              //数组1的中位比数组2的中位小k -= newIndex1 - index1 + 1;    //排除index1 = newIndex1 + 1;}else {k -= newIndex2 - index2 + 1;    //排除index2 = newIndex2 + 1;}} }double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {int totalLen = nums1.size() + nums2.size();if (totalLen % 2 == 1)           //总长为奇数return getKthElement(nums1, nums2, (totalLen + 1) / 2);else                            //总长为偶数return (getKthElement(nums1, nums2, totalLen / 2) + getKthElement(nums1, nums2, totalLen / 2 + 1))/ 2.0;}};