1 Studying《Computer Vision: Algorithms and Applications 2nd Edition》11-15
目录
Chapter 11 Structure from motion and SLAM
11.1 几何内禀校准
11.2 姿态估计
11.3 从运动中获得的双帧结构
11.4 从运动中提取多帧结构
11.5 同步定位与建图(SLAM)
11.6 额外阅读
Chapter 12 Depth estimation
12.1 极点几何
12.2 稀疏对应
12.3 密集通信
12.4 地方方法
12.5 全球优化
12.6 深度神经网络
12.7 多视图立体
12.8 单眼深度估计
12.9 额外阅读
12.10 练习
Chapter 13 3D reconstruction
13.1 从X中获得形状
13.2 三维扫描
13.3 表面表示
13.4 基于点的表示
13.5 容量表示
13.6 基于模型的重建
13.7 恢复纹理贴图和反照率
13.8 附加阅读材料
13.9 练习
Chapter 14 Image-based rendering
14.1 视图插值
14.2 层状深度图像
14.3 光场和光图
14.4 环境问题
14.5 基于视频的渲染
14.6 神经渲染
14.7 附加阅读材料
14.8 练习
Chapter 15 Conclusion
Chapter 11 Structure from motion and SLAM
11.1几何内禀校准 685
11.1.1消失点 687
11.1.2应用:单视图计量 688
11.1.3旋转运动 689
11.1.4径向畸变 691
11.2姿态估计 693
11.2.1线性算法 693
11.2.2迭代非线性算法 695
11.2.3应用:位置识别 698
11.2.4三角测量 701
11.3从运动中获得的双帧结构 703
11.3.18、7和5点算法 703
11.3.2特殊动线和结构 708
11.3.3投影(未校准)重建 710
11.3.4自校准 712
11.3.5应用:查看变形 714
11.4从运动中提取多帧结构 715
11.4.1因式分解 715
11.4.2捆绑调整 717
11.4.3利用稀疏性 719
11.4.4应用:匹配移动 723
11.4.5不确定性和模糊性 723
11.4.6应用:从网络照片中重建 725
11.4.7从运动中获取全局结构 728
11.4.8结构和运动受限 731
11.5同步定位与建图(SLAM) 734
11.5.1应用:自主导航 737
11.5.2应用:智能手机增强现实 739

图11.1运动结构示例:(a)二维校准目标(张2000)©2000 IEEE;(b)单视图测量(克里米尼西、里德和齐瑟曼2000)©2000斯普林格。(c–d)线匹配(施密德和齐瑟曼1997)©1997 IEEE;(e–g)特拉法加广场、中国长城和布拉格老城广场的三维重建(斯纳维利、塞茨和泽利斯基2006)©2006 ACM;(h)智能手机增强现实显示实时深度遮挡效果(瓦伦丁、科德尔等人2018)©2018 ACM。
从图像重建三维模型自计算机视觉诞生以来一直是其核心主题之一(图1.7)。事实上,当时人们认为构建三维模型是场景理解和识别的前提条件(Marr1982),尽管近几十年的工作已经证明了这一点。然而,三维建模在虚拟旅游(第11.4.6节)、自主导航(第11.5.1节)和增强现实(第11.5.2节)等应用中也被证明具有极大的价值。
在前三个章节中,我们专注于建立二维图像之间对应关系的技术,并将其应用于图像拼接、视频增强和计算摄影等多种场景。本章我们将探讨如何利用这些对应关系构建场景的稀疏三维模型,并根据这些模型重新定位相机。尽管这一过程通常涉及同时估计三维几何(结构)和相机姿态(运动),但出于历史原因,它常被称为运动从结构(Ullman1979)。
射影几何和运动结构这两个主题极其丰富,已经有一些优秀的教科书和综述文章对此进行了阐述(Faugeras和Luong 2001;Hartley和Zisserman 2004;Moons、Van Gool和Vergauwen 2010;Ma、Soatto等2012)。本章跳过了这些书中许多更丰富的材料,例如三焦张量和用于完全自校准的代数技术,而是集中讨论了我们在大规模基于图像的重建问题中发现有用的基理论(Snavely、Seitz和Szeliski 2006)。
我们在第11.1节开始本章,回顾常用的相机内参校准技术,例如我们在第2.1.4–2.1.5节中介绍的焦距和径向畸变参数。接下来,我们讨论如何从三维到二维点对应关系估计相机的外参姿态(第11.2节),以及如何通过三角测量一组二维对应关系来估计一个点的三维位置。然后,我们探讨两帧结构从运动问题(第11.3节),该问题涉及确定两个相机之间的极线几何关系,也可以利用自校准恢复某些关于相机内参的信息(第11.3.4节)。第11.4.1节研究了使用正交投影模型近似同时估计大量点轨迹的结构和运动的方法。随后,我们发展了一种更通用且有用的结构从运动方法,即所有相机和三维结构参数的同时束调整(第11.4.2节)。我们还探讨了场景中存在更高层次结构,如直线和平面时出现的特殊情况(第11.4.8节)。本章的最后一部分(第11.5节),我们研究了实时系统中的同时定位与建图(SLAM),该系统在移动过程中重建三维世界模型,并可应用于视觉
11.1 几何内禀校准
正如我们在下一节(公式(11.14–11.15))中讨论的,相机内部(内在)校准参数的计算可以与相机相对于已知校准目标的姿态估计同时进行。这确实是摄影测量学(Slama1980)和计算机视觉(Tsai1987)领域中常用的“经典”相机校准方法。在本节中,我们将探讨一些更简单的替代方案,这些方案可能不需要完全解决非线性回归问题,使用不同的校准目标,并估计相机光学的非线性部分,如径向畸变。在某些应用中,可以利用与JPEG图像关联的EXIF标签来粗略估计相机的焦距,从而初始化迭代估计算法;但这种方法应谨慎使用,因为结果往往不准确。
校准模式
使用校准图案或一组标记是估计相机内参的一种较为可靠的方法。在摄影测量中,通常会将相机放置在一个大范围内,观察远处的校准目标,这些目标的确切位置已通过测量设备预先计算(Slama 1980;Atkinson 1996;Kraus 1997)。在这种情况下,姿态的平移分量变得无关紧要,只需恢复相机的旋转和内参参数。
如果需要使用较小的校准装置,例如用于室内机器人应用或携带自身校准目标的移动机器人,最好让校准对象尽可能覆盖工作空间的大部分(图11.2a),因为平面目标往往无法准确预测远离平面的姿态组件。判断校准是否成功的一个好方法是估计参数的协方差(第8.1.4节),然后将工作空间中不同点的3D点投影到图像中,以估计它们的2D位置不确定性。
如果没有校准图案,也可以同时进行结构和姿态恢复的校准(第11.1.3节和第11.4.2节),这被称为自校准(Faugeras、Luong和Maybank 1992;Pollefeys、Koch和Van Gool 1999;Hartley和Zisserman 2004;Moons、Van Gool和Vergauwen 2010)。然而,这种方法需要大量的图像才能准确。

图11.2校准图案:(a)三维目标(Quan和Lan1999)©1999 IEEE;(b)二维目标(Zhang2000)©2000 IEEE。注意,需要从这些图像中去除径向畸变,才能使用特征点进行校准。
平面校准图案
当使用有限的工作空间且具备精确的加工和运动控制平台时,一种良好的校准方法是将平面校准目标移动到工作空间内,并利用已知的三维点位置进行校准。这种方法有时被称为N-平面校准法(Gremban、Thorpe和Kanade 1988;Champleboux、Lavall e等1992b;Grossberg和Nayar 2001),其优点在于每个相机像素都可以映射到空间中的一个独特的三维点,这不仅考虑
了由校准矩阵K建模的线性效应,还考虑了非线性效应,如径向畸变(第11.1.4节)。
通过在相机前挥动平面校准图案(图11.2b),可以获得一个较为简便但精度较低的校准。在这种情况下,需要结合内参恢复图案的姿态。在~此技术中,每张输入图像用于计算一个单独的单应性(8.19–8.23)H,将平面校准点(Xi,Yi,1)映射到图像坐标(xi,yi),
(11.1)
其中,ri是R的前两列,~表示至多按比例相等。从这些数据中,张(2000)展示了如何对B = K-TK-1矩阵中的九个条目形成线性约束,从而可以使用矩阵恢复校准矩阵K。

图11.3从消失点进行校准:(a)任意一对有限消失点
(i,j)可用于估计焦距;(b)消失点的正交中心
三角形给出了图像c的图像中心。
平方根和逆运算。矩阵B在射影几何中被称为绝对圆锥(IAC)的像,常用于相机校准(Hartley和Zisserman 2004,第8.5节)。如果只需要恢复焦距,则可以采用下面描述的更简单的使用消失点的方法。
在实际应用中,校准的一个常见情况是相机拍摄到具有长条形图案的制造或建筑场景,如盒子或建筑物墙壁。在这种情况下,我们可以将对应于三维平行线的二维线相交,以计算它们的消失点,具体方法见第7.4.3节,并利用这些消失点来确定内参和外参(Caprile和Torre 1990;Becker和Bove 1995;Liebowitz和Zisserman 1998;Cipolla、Drummond和Robertson 1999;Antone和Teller 2002;Criminisi、Reid和Zisserman 2000;Hartley和Zisserman 2004;Pflugfelder 2008)。
假设我们检测到了两个或更多的正交消失点,且这些消失点都是有限的,即它们不是由图像平面上看似平行的线获得的(图11.3a)。我们还假设校准矩阵K的形式简化,其中只有焦距未知(2.59)。通常,在进行粗略的3D建模时,可以假设光学中心位于图像中心,长宽比为1,并且没有倾斜。在这种情况下,消失点的投影方程可以表示为
= ri , (11.2)
其中,pi对应于一个基本方向(1,0,0)、(0,1,0)或(0,0,1),ri

图11.4单视图测量(Criminisi、Reid和Zisserman 2000)©2000斯普林格:(a)输入图像显示了从两个水平消失点计算出的三个坐标轴(这些消失点可以从棚屋的侧边确定);(b)三维重建的新视图。
是旋转矩阵R的第i列。
从旋转矩阵的列之间的正交性,我们有
ri·rj ~(xi - cx)(xj - cx)+(yi - cy)(yj - cy)+ f2 = 0,i j
(11.3)
从中我们可以得到f2的估计值。请注意,随着消失点逐渐靠近图像中心,该估计值的准确性会提高。换句话说,最好将校准图案在45°轴附近倾斜一定角度,如图11.3a所示。一旦确定了焦距f,就可以通过归一化(11.2)的左侧并取叉积来估计R的各个列。或者,也可以使用正交普罗克鲁斯特算法(8.32)。
如果三个消失点在同一图像中均可见且有限,则可以将图像中心估计为由这三个消失点形成的三角形的垂心(Caprile和Torre 1990;Hartley和Zisserman 2004,第8.6节)(图11.3b)。然而,在实际操作中,使用非线性最小二乘法重新估计任何未知的内部校准参数更为准确(11.14)。
一个有趣的视点估计和相机校准应用是Criminisi、Reid和Zisserman(2000)开发的单视图测量系统。该系统允许人们交互式地测量高度和其他尺寸,以及构建分段平面3D模型,如图11.4所示。
系统的第一步是在地面平面上识别两个正交的消失点以及垂直方向上的消失点,这可以通过在图像中绘制一些平行线来完成。或者,可以使用第7.4.3节讨论的自动化技术或Schaffalitzky和Zisserman(2000)的方法。然后,用户可以在图像中标记几个尺寸,例如参考物体的高度,系统可以自动计算另一个物体的高度。墙壁和其他平面假象(几何形状)也可以勾画并重建。
在克里米尼西、里德和齐瑟曼(2000)最初开发的公式中,系统生成一个仿射重建,即仅已知每个轴上的独立缩放因子。通过假设相机校准到未知焦距,可以构建一个更有用的系统,这可以从正交(有限)消失方向恢复,正如我们在第11.1.1节中所描述的那样。一旦完成这一过程,用户可以在地面上指定一个原点,并指出另一个已知距离外的点。由此,地面上的点可以直接投影到三维空间中,而地面上方的点与它们的地平面投影配对后也可以被恢复。这样,场景的完全度量重建就成为可能。
练习11.4要求你实现这样一个系统,并用它来建模一些简单的3D场景。第13.6.1describes节介绍了其他可能的多视角建筑重建方法,包括一个使用消失点建立三维线方向和平面法向量的交互式分段平面建模系统(Sinha,Steedly等,2008)。
11.1.3旋转运动
当没有校准目标或已知结构,但可以围绕相机的前节点旋转(或者,等效地,在一个所有物体都远离的大型开放环境中工作)时,可以通过假设从一组重叠图像中对相机进行校准
如图11.5所示,它正在进行纯旋转运动(Stein1995;Hartley
1997b;Hartley、Hayman等人2000;de Agapito、Hayman和Reid 2001;Kang和Weiss 1999;Shum和Szeliski 2000;Frahm和Koch 2003)。当使用完整的360°运动进行校准时,可以获得非常精确的焦距f估计值,因为这种估计的准确性与最终圆柱全景图中的总像素数成正比(第8.2.6节)(Stein 1995;Shum和Szeliski 2000)。
要使用这项技术,我们首先计算所有重叠图像对之间的单应性矩阵ij,如公式(8.19–8.23)所示。然后,利用观察到的现象,首次在公式(2.72)中提出并在公式(8.38)中详细探讨,即每个单应性矩阵都通过(未知的)校准矩阵Ki与相机间旋转Rij相关。

图11.5使用手持摄像机拍摄的四幅图像,使用三维旋转运动模型进行配准,可用于估计摄像机的焦距(Szeliski和Shum1997)©2000 ACM。
Hij = KiRi Rj-1Kj-1 = KiRijKj-1。 (11.4)
获取校准的最简单方法是使用校准矩阵(2.59)的简化形式,假设像素为正方形且图像中心位于二维像素阵列的几何中心,即Kk =对角线(fk,fk,1)。我们从原始像素坐标中减去一半的宽度和高度,使得像素(x,y)=(0,0)位于图像中心。然后我们可以将公式(11.4)重写为
其中hij是H10的元素。
利用旋转矩阵R10的正交性质和(11.5)的右侧仅已知到一个比例因子这一事实,我们得到
h0 + h1 + f0-2h2 = h + h + f0-2h (11.6)
和
h00 h10 + h01 h11 + f0-2h02 h12 = 0. (11.7)
或
如果h00
h10 -h01
h11。 (11.9)
如果这两个条件都不满足,我们也可以计算第一(或第二)行~与第三行的点积。通过分析H10的列,同样可以得到f1的结果。如果两幅图像的焦距相同,我们可以取f0和f1的几何平均值作为估计的焦距f=√f1 f0。当有多组f的估计值时,例如来自不同的单应性变换,可以使用中位数作为最终估计值。对于固定参数相机Ki = K的情况,可以使用Hartley(1997b)的技术获得更一般的(上三角)K的估计值。Hartley、Hayman等人(2000)和de Agapito、Hayman和Reid(2001)讨论了时间变化校准参数和非静态相机情况下的扩展。
通过构建完整的360°全景图,可以显著提高相机参数的质量。因为如果焦距估计错误,当序列中的第一张图像与自身拼接时(图8.6),会导致间隙(或过度重叠)。由此产生的错位可用于改进焦距估计,并重新调整旋转估计,如第8.2.4节所述。围绕光轴旋转相机90°并重新拍摄全景图是检查纵横比和像素偏斜问题的好方法,当有足够的纹理时,生成完整的半球全景图也是不错的选择。
然而,最终,如第11.2.2节所述,可以使用固有参数和外在参数(旋转)的完整同时非线性最小化来获得校准参数(包括径向畸变)的最准确估计值。
当使用广角镜头拍摄图像时,通常需要建模镜头畸变,如径向畸变。正如第2.1.5节所述,径向畸变模型指出,观测图像中的坐标会根据其径向距离成比例地向中心偏移(桶形畸变)或远离中心(枕形畸变)(图2.13a–b)。最简单的径向畸变模型使用低阶多项式(参见公式(2.78)),
= x(1 + h1 r2 + h2 r4 ) = y(1 + h1 r2 + h2 r4 ),
其中(x,y) = (0,0)在径向畸变中心(2.77),r2 = x2 + y2,h1和h2称为径向畸变参数(Brown1971;Slama1980)。1
有时,x和之间的关系用相反的方式表示,即在右侧使用带撇号(最终)的坐标,x =(1 + 12 + 24)。如果我们将图像像素映射到(扭曲的)
可以使用多种技术来估计给定镜头的径向畸变参数,前提是数码相机在其捕捉软件中尚未完成此操作。最简单且最有用的方法之一是拍摄一个包含大量直线的场景图像,特别是那些与图像边缘对齐或靠近边缘的直线。然后调整径向畸变参数,直到图像中的所有直线都变得笔直,这通常被称为铅垂线法(Brown 1971;Kang 2001;El-Melegy和Farag 2003)。练习11.5给出了如何实现这种技术的一些更多细节。
另一种方法是使用多个重叠的图像,并将径向畸变参数的估计与图像对齐过程相结合,即扩展第8.3.1节中用于拼接的流程。Sawhney和Kumar(1999)采用了一种从粗到精的策略,结合了运动模型(平移、仿射、投影)层次结构和二次径向畸变校正项。他们使用直接(基于强度的)最小化方法来计算对齐。Stein(1997)则采用基于特征的方法,结合通用的3D运动模型(以及二次径向畸变),这需要比无视差旋转全景图更多的匹配点,但可能更为通用。更近期的方法有时同时计算未知的内部参数和径向畸变系数,这些系数可能包括高阶项或更复杂的有理或非参数形式(Claus和Fitzgibbon 2005;Sturm 2005;Thirthala和Pollefeys 2005;Barreto和Daniilidis 2005;Hartley和Kang 2005;Steele和Jaynes 2006;Tardif、Sturm等2009)。
当使用已知的校准目标时(图11.2),径向畸变估计可以融入其他内参和外参的估计中(张2000;哈特利和康2007;塔迪夫、斯特姆等人2009)。这可以视为在图11.7所示的一般非线性最小化流程中,在内参乘法框fC和透视分割框fP之间增加了一个阶段。(有关平面校准目标情况的更多细节,请参见练习11.6。)
当然,如第2.1.5节所述,有时可能需要更通用的镜头畸变模型,例如鱼眼和非中心投影。虽然这类镜头的参数化可能更为复杂(第2.1.5节),但通常可以采用使用已知三维位置的校准装置或通过场景的多个重叠图像进行自校准的方法(Hartley和Kang 2007;Tardif、Sturm和Roy 2007)。用于校正径向畸变的技术同样也可以用来减少色差,通过分别校准每个颜色通道来实现。
然后扭曲光线以获得空间中的三维光线,即,如果我们使用逆变形。
11.2 姿态估计
基于特征的对齐的一个常见实例是从一组二维点投影中估计物体的三维姿态。这种姿态估计问题也被称为外参校准,与我们将在第11.1节讨论的内部相机参数如焦距的内参校准相对。从三个对应点恢复姿态的问题,即所需最少信息量的问题,被称为透视三点问题(P3P),并扩展到更多点的问题,统称为PnP(Haralick,Lee等1994;Quan和Lan1999;Gao,Hou等2003;Moreno-Noguer,Lepetit和Fua2007;Persson和Nordberg2018)。
在本节中,我们将研究一些为解决此类问题而开发的技术,首先从直接线性变换(DLT)开始,它恢复了3×4相机矩阵,然后是其他“线性”算法,最后是统计最优迭代算法。
恢复相机姿态的最简单方法是形成一组类似于用于2D运动估计(8.19)的有理线性方程,从透视投影(2.55–2.56)的相机矩阵形式中得到,
(11.11)
(11.12)
其中(xi,yi)是测量的二维特征位置,(Xi,Yi,Zi)是已知的三维特征位置(图11.6)。与公式(8.21)类似,这个方程组可以通过在线性方式求解相机矩阵P中的未知数,方法是将方程两边的分母相乘。由于P在比例上是未知的,我们可以固定其中一个元素,例如p23 = 1,或者找到一组线性方程组的最小奇异向量。由此产生的算法称为直接线性变换(DLT),通常归功于Sutherland(1974年)。(关于更深入的讨论,请参见Hartley和Zisserman(2004年)。)为了计算P中的12个(或11个)未知数,至少需要知道3D和2D位置之间的六个对应关系。
与估计同态(8.21–8.23)的情况一样,通过直接最小化方程组(11.11–11.12),可以获得P中条目的更准确的结果
2“三点”算法实际上需要第四个点来解决四重模糊性。

图11.6通过直接线性变换和测量点对之间的视觉角度和距离进行姿态估计。
用少量迭代进行非线性最小二乘法。注意,与(11.11–11.12)中取X/Z和Y/Z值的比值不同,也可以取交叉
将3维向量(xi,yi,1)的图像测量值与三维射线(X,Y,Z)相乘,并将该交叉乘积的三个元素设为0。当将所得的三个方程解释为一组最小二乘约束时,实际上计算了两条射线之间角度的正弦平方。
一旦恢复了P中的条目,就可以通过观察方程(2.56)恢复内在校准矩阵K和刚性变换(R,t),
P = K[Rjt]. (11.13)
由于K是上三角矩阵(参见第2.1.4节中的讨论),因此可以使用RQ分解法从P的前3×3子矩阵中获得K和R(Golub和Van Loan,1996)。3
然而,在大多数应用中,我们对固有的校准矩阵K有一些先验知识,例如像素是方形的,偏斜非常小,图像中心接近图像的几何中心(2.57–2.59)。这些约束可以被纳入到K和(R,t)参数的非线性最小化过程中,如Section11.2.2所述。 在相机已经校准的情况下,即矩阵K已知(第11.1节),我们可以使用最少三个点进行姿态估计(Fischler和Bolles 1981;Haralick、Lee等人1994;Quan和Lan 1999)。这些线性PnP(透视n点)算法的基本观察是,任意一对二维点i和j之间的视角度必须与它们对应的三维点pi和之间的角度相同。
3注意术语的不幸冲突:在矩阵代数教科书中,R代表一个上三角矩阵;在计算机视觉中,R是一个正交旋转。
本书第一版(Szeliski 2010,第6.2.1节)以及(Quan和Lan 1999)中详细推导了这种方法。这些文献中,作者提供了该方法及其他技术的精度结果,后者虽然使用较少的点数,但需要更复杂的代数运算。Moreno-Noguer、Lepetit和Fua(2007)的文章回顾了其他替代方案,并提出了一种复杂度更低且通常产生更准确结果的算法。Terzakis和Lourakis(2020)则在一篇更为近期的论文中综述了过去十年发表的相关研究。
不幸的是,由于最小化PnP解决方案可能非常敏感于噪声,并且还存在浮雕模糊问题(例如深度反转)(第11.4.5节),因此明智的做法是使用第11.2.2节中描述的迭代技术来优化PnP的初始估计。另一种姿态估计算法是从一个缩放后的正射投影模型开始,然后使用更精确的透视投影模型逐步改进这一初始估计(DeMenthon和Davis1995)。正如论文标题所述,该模型的魅力在于它可以“用25行[Mathematica]代码”实现。
基于CNN的姿态估计
与其他计算机视觉领域一样,深度神经网络也被应用于姿态估计。一些具有代表性的论文包括Xiang、Schmidt等人(2018年)、Oberweger、Rad和Lepetit(2018年)、Hu、Hugonot等人(2019年)、Peng、Liu等人(2019年)以及(Hu、Fua等人2020年)关于物体姿态估计的研究,还有Kendall和Cipolla(2017年)及Kim、Dunn和Frahm(2017年)在第11.2.3节中讨论的位置识别研究。此外,围绕从RGB-D图像中估计姿态的社区也非常活跃,最近的论文(Hagelskjær和Buch2020;Labb、Carpentier等人2020)在该领域进行了评估。
BOP(6DOF物体姿态基准)(Hoda,Michel等人,2018)。4
估计姿态最准确且灵活的方法是直接最小化二维点的平方(或鲁棒)重投影误差,作为未知姿态参数(R;t)的函数,并可选地使用非线性最小二乘法(Tsai1987;Bogart1991;Gleicher和Witkin1992)来最小化K。我们可以将投影方程表示为
xi = f(pi;R
;t;K) (11.14)
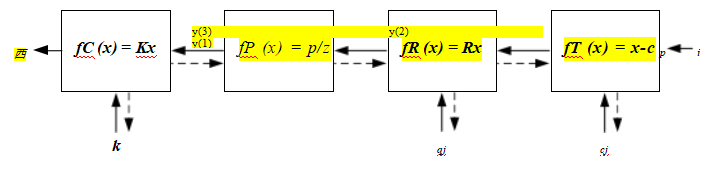
图11.7通过一系列变换f(k)将三维点pi投影到二维测量值xi,每项变换都由其自身的参数集控制。虚线表示在反向传播过程中计算偏导数时的信息流。
ENLP =
(11.15)
其中,ri = i -
i是当前残差向量(预测位置的二维误差)和
偏导数是关于未知姿态参数(旋转、平移,以及可选的校准)的。我们首次在第4.1.3节的(4.15)中介绍的鲁棒损失函数P,用于减少异常对应的影响。请注意,如果2D特征位置有完整的2D协方差估计,则上述平方范数可以由逆点协方差矩阵加权,如公式(8.11)所示。
一个更容易理解(和实现)的上述非线性回归问题可以通过将投影方程重写为一系列更简单的步骤来构建,每个步骤都通过简单的变换如平移、旋转或透视除法来转换一个四维齐次坐标pi(图11.7)。由此产生的投影方程可以表示为
y (1) = fT (pi ; cj) = pi - cj , (11.16)
y (2) = fR (y (1) ; qj) = R (qj) y (1) , (11.17)
xi = fC(y(3);k)= K(k) y(3)。 (11.19)
请注意,在这些方程中,我们用索引j对相机中心cj和相机旋转四元数qj进行了索引,以防使用校准对象的多个姿态(参见第11.4.2节)。我们还使用相机中心cj而不是世界平移tj,因为这是一个更自然的参数来估计。
这一组变换的链式结构的优点在于,每个变换都对其参数和输入具有简单的偏导数。因此,一旦预测值
参数(cj;qj;k),我们可以使用链式法则得到所有需要的偏导数
(11.20)
其中p(k)表示正在优化的参数向量之一。(同样的“技巧”在神经网络中作为反向传播的一部分使用,我们在Figure5.31中介绍过。)
在这个公式中,可以显著简化的一个特殊情况是旋转更新的计算。不必直接计算3×3旋转矩阵R(q)关于单位四元数元素的导数,而是可以在当前旋转矩阵前加上方程(2.35)给出的增量旋转矩阵△R(!),然后计算变换对这些参数的偏导数,这会导致一个简单的逆向链偏导数与输出的三维向量的叉积,如方程(2.36)所解释的那样。
姿态估计的一个广泛应用是增强现实,其中虚拟的3D图像或注释被叠加到实时视频流上,无论是通过透明眼镜(前置显示)还是普通计算机或移动设备屏幕(Azuma,Baillot等2001;Haller,Billinghurst和Thomas 2007;Billinghurst,Clark和Lee 2015)。在某些应用中,卡片或书籍上的特殊图案会被跟踪以实现增强效果(Kato,Billinghurst等2000;Billinghurst,Kato和Poupyrev 2001)。对于桌面应用程序,嵌入增强鼠标中的摄像头可以跟踪打印在鼠标垫上的点阵,使用户能够控制其在三维空间中的六个自由度的位置和方向(Hinckley,Sinclair等1999)。如今,追踪已知目标如电影海报的功能被用于一些基于手机的增强现实系统,例如Facebook的Spark AR。
有时,场景本身提供了一个方便的追踪对象,例如用于镜头后方摄像机控制的矩形桌面(Gleicher和Witkin 1992)。在户外地点,如电影拍摄现场,通常会在场景中放置特殊标记,比如鲜艳的彩色球体,以便更容易找到和追踪它们(Bogart 1991)。在较旧的应用中,使用了测量技术来确定这些球体的位置。
在拍摄前,现在更常见的是将结构从运动直接应用到影片本身(第11.5.2节)。
练习8.4要求你为增强现实应用程序实现一个跟踪和姿态估计系统。
姿态估计最令人兴奋的应用之一是在位置识别领域,这既可用于桌面应用程序(“我拍的这张度假照片是在哪里拍的?”),也可用于移动智能手机应用程序。后者不仅包括根据手机图像确定当前位置,还提供导航方向或在图像中标注有用信息,如建筑物名称和餐厅评论(即便携式增强现实)。这个问题也常被称为视觉(或基于图像)定位(Se,Lowe,和Little 2002;Zhang和Kosecka 2006;Janai,
G ney等人,2020年,第13.3节)或视觉位置识别(Lowry,S.nderhauf等人,2015)。
一些定位识别方法假设照片包含建筑场景,可以使用消失方向预先校正图像以方便匹配(Robertson和Cipolla 2004)。其他方法则利用一般的仿射协变兴趣点进行宽基线匹配(Schaffalitzky和Zisserman 2002),在2005年国际计算机视觉竞赛中获胜的参赛作品(Szeliski 2005)采用了这种方法(Zhang和Kosecka 2006)。Snavely、Seitz和Szeliski(2006)提出的“照片旅游”系统(第14.1.2节)首次将这些理念应用于大规模图像匹配和(隐式)从互联网照片集合中进行位置识别,这些照片是在各种观看条件下拍摄的。
位置识别的主要难点在于处理像Flickr (Philbin,Chum等2007;Chum,Philbin等2007;Philbin,Chum等2008;Irschara,Zach等2009;Turcot和Lowe 2009;Sattler,Leibe和Kobbelt 2011,2017)或商业捕获数据库(Schindler,Brown和Szeliski 2007;Klingner,Martin和Roseborough 2013;Tori,Arandjelovi等2018)中极其庞大的社区(用户生成)照片集合。常见元素如树叶、标志和普通建筑元素的普遍出现进一步增加了任务的复杂性(Schindler,Brown
,和Szeliski 2007;Jegou,Douze,和Schmid 2009;Chum和Matas 2010b;Knopp,Sivic和Pajdla 2010;Tori,Sivic等2013;Sattler,Havlena等2016)。图7.26展示了一些来自社区照片集合的位置识别结果,而图11.8则展示了更密集的商业捕获数据集的样本结果。在后一种情况下,相邻数据库图像之间的重叠可以用来验证和剔除潜在匹配项,即要求查询图像与附近的重叠部分相匹配——

图11.8基于特征的位置识别(Schindler、Brown和Szeliski2007)©
2007 IEEE:(a)三组重叠的街道照片;(b)手持相机拍摄的照片和(c)相应的数据库照片。
在匹配之前先比对数据库图像。类似的想法已被用于改进全景视频序列中的位置识别(Levin和Szeliski 2004;Samano、Zhou和Calway 2020),以及将图像序列中的局部SLAM重建与预计算地图进行匹配以提高可靠性(Stenborg、Sattler和Hammarstrand 2020)。在建筑物和购物中心内识别室内位置也面临一系列挑战,包括无纹理区域和重复元素(Levin和Szeliski 2004;Wang、Fidler和Urtasun 2015;Sun、Xie等2017;Taira、Okutomi等2018;Taira、Rocco等2019;Lee、Ryu等2021)。地面图像与航拍图像的匹配研究也已开展(Kaminsky、Snavely等2009;Shan、Wu等2014)。
一些早期关于位置识别的研究围绕牛津5公里和巴黎6公里数据集(Philbin,Chum等,2007,2008;Radenovi,Iscen等,2018)以及维也纳(Irschara,Zach等,2009
)和照片旅游(Li,Snavely,和Huttenlocher,2010)数据集展开,后来又围绕7个室内RGB-D场景数据集(Shotton,Glocker等,2013)和剑桥地标(Kendall,Grimes,和Cipolla,2015)进行。NetVLAD论文(Arandjelovic,Gronat等,2016)在谷歌街景时间机器数据上进行了测试。目前,最广泛使用的视觉定位数据集是在长期视觉定位基准6收集的,包括如亚琛日夜间(Sattler,Maddern等,2018)和InLoc (Taira,Okutomi等,2018)。虽然大多数定位系统基于地面图像集合工作,但也可以根据纹理数字高程(地形)模型重新定位,用于户外(非城市)应用(Baatz,Saurer等。
Al.2012;Brejcha,Luk et al
.2020)。
最近的一些定位方法使用深度网络生成特征描述符(Arandjelovic,Gronat等2016;Kim,Dunn和Frahm 2017;Torii,Arandjelovi等2018;Radenovi,Tolias和Chum
2019;Yang,Kien Nguyen等2019
;Sarlin,Unagar等2021),进行大规模实例检索(Radenovi,Tolias和Chum 2019;Cao,Araujo和Sim 2020;Ng
,Balntas等2020;Tolias,Jenicek和Chum 2020;Pion,Humenberger等2020和第6.2.3节),将图像映射到3D场景坐标(Brachmann和Rother 2018),或执行端到端场景坐标回归(Shotton,Glocker等2013),绝对姿态回归(APR)(Kendall,Grimes和Cipolla 2015;Kendall和Cipolla 2017),或相对姿态回归(RPR)(Melekhov,Ylioinas等2017;Balntas,Li和Prisacariu 2018)。这些技术的最新评估表明,基于特征匹配随后进行几何姿态优化的经典方法通常在准确性和泛化能力方面优于姿态回归方法(Sattler,Zhou等2019;Zhou,Sattler等2019;Ding,Wang等2019;Lee,Ryu等2021;Sarlin,Unagar等2021)。
长期视觉定位基准有一个排行榜,列出了表现最好的定位系统。在CVPR 2020研讨会和挑战中,一些获胜的en-
尝试基于最近的检测器、描述符和匹配器,如SuperGlue (Sarlin,DeTone等2020)、ASLFeat (Luo,Zhou等2020)和R2D2 (Revaud,Weinzaepfel等2019)。其他表现良好的系统包括HF-Net (Sarlin,Cadena等2019)、ONavi (Fan,Zhou等2020)和D2-Net (Dusmanu,Rocco等2019)。更近的趋势是使用深度神经网络或变压器来建立密集的粗到精匹配(Jiang,Trulls等2021;Sun,Shen等2021)。
位置识别的另一种变体是地标自动发现,即经常拍摄的对象和地点。Simon、Snavely和Seitz(2007)展示了如何通过分析照片旅游中三维建模过程中构建的匹配图来发现这些对象。最近的研究扩展了这种方法,使用高效的聚类技术处理更大的数据集(Philbin和Zisserman 2008;Li、Wu等2008;Chum、Philbin和Zisserman 2008;Chum和Matas 2010a;Aranđelovi和Zisserman 2012),结合GPS和文本标签等元数据与视觉搜索(Quack、Leibe和Van Gool 2008;Crandall、Backstrom
等2009;Li、Snavely等2012),并利用多个描述符在微型空中车辆导航中实现实时性能(Lim、Sinha等2012)。现在甚至可以基于多个松散标记图像中的共现情况自动关联对象标签(Simon和Seitz 2008;Gammeter、Bossard等2009)。
按地点组织世界照片收藏的概念甚至已经被重新定义

图11.9使用天体测量法定位星场,https://astrometry.net。(a)输入星场和一些选定的星四边形。(b)星体C和D的二维坐标相对于由A和B定义的单位正方形进行编码。
最近扩展到将宇宙中(天文学)的所有照片组织在一个名为天体测量的应用程序中。7用于匹配任意两个星场的技术是取附近恒星的四重组合(一对恒星和另一对位于它们直径内的恒星),通过使用内切正方形作为参考框架来编码第二对点的相对位置,形成一个30位的几何哈希值,如图11.9所示。然后使用传统信息检索技术(为天空图集的不同部分构建的k-d树)来查找匹配的四重组合作为潜在的星场位置假设,这些假设可以通过相似性变换进行验证。
从一组对应的图像位置和已知的相机位置确定一个点的三维位置的问题被称为三角测量。这个问题与我们在第11.2节中研究的姿态估计问题相反。
解决这个问题最简单的方法之一是找到与相机{Pj = Kj [Rj jtj ]}观察到的二维匹配特征位置{xj }对应的全部三维射线最近的三维点p,其中tj =—Rj cj,cj为第j个相机中心(2.55–2.56)。
如图Figure11.10所示,这些射线从cj出发,方向为j = N(Rj-1Kj-1xj),
其中N(v)将向量v归一化为单位长度。这条射线上与p最近的点,即
我们用qj = cj + dj j来表示,以使距离最小
Ⅱqj — pⅡ2 = Ⅱcj + dj j — pⅡ2 ; (11.21)
在dj = j·(p—cj)处取最小值。因此,
qj = cj + (j )(p — cj) = cj + (p — cj) Ⅱ ; (11.22)

图11.10通过查找最接近所有光学光线cj + dj j的点p来实现三维点三角化。
在公式(2.29)的符号中,p和qj之间的平方距离为
r = Ⅱ(I - j )(p - cj )Ⅱ2 = Ⅱ(p - cj )丄 Ⅱ2 . (11.23)
p的最优值,即最接近所有光线的值,可以作为一个规则计算。
最小二乘问题,通过求和所有r并找到p的最优值,
(11.24)
另一种替代公式,更具有统计学上的最佳性,如果某些摄像机比其他摄像机更接近于三维点,则可以产生显著更好的估计值,即最小化测量方程中的残差
其中(xj,yj)是测量的二维特征位置,{p0()... p2()}是相机矩阵Pj中的已知条目(Sutherland1974)。
与方程(8.21、11.11和11.12)一样,这组非线性方程可以通过乘以分母的两边转换为一个线性最小二乘问题,再次得到直接的线性变换(DLT)形式。请注意,如果我们使用齐次坐标p =(X,Y,Z,W),则所得方程组是齐次的。
最佳解决方法是奇异值分解(SVD)或特征值问题(寻找最小的奇异向量或特征向量)。如果我们设W = 1,可以使用常规线性最小二乘法,但所得系统可能奇异或条件不良,即当所有视射线平行时,这种情况发生在远离相机的点上。
因此,通常最好使用齐次坐标来参数化三维点,特别是当我们知道相机与这些点之间的距离可能相差很大时。当然,无论选择何种表示方法,使用非线性最小二乘法(如公式8.14和8.23所述)来最小化观测集(11.25–11.26),都优于使用线性最小二乘法。
对于两个观测点的情况,事实证明,能够精确最小化真实重投影误差(11.25–11.26)的点p的位置可以通过六次多项式方程的解来计算(Hartley和Sturm 1997)。三角测量中需要注意的另一个问题是手性问题,即确保重建的点位于所有相机前方(Hartley 1998)。虽然这并不总是可以保证的,但一个有用的启发式方法是取那些位于相机后方的点,因为它们的光线是发散的(想象图11.10中的光线彼此远离),并将这些点设置在无穷远平面上,通过将它们的W值设为0。
11.3 从运动中获得的双帧结构
到目前为止,在我们对三维重建的研究中,一直假设要么已知三维点的位置,要么已知三维相机的姿态。在本节中,我们将首次探讨运动从结构法,即从图像对应关系同时恢复三维结构和姿态。特别是,我们研究仅基于两帧点对应的技术。我们将这一部分分为经典“n点”算法的研究、特殊情况(退化情况)、投影(未校准)重建以及未知内参的相机自校准。
考虑图11.11,该图展示了从两个相机视角观察到的三维点p,这两个相机的相对位置可以通过旋转R和平移t来编码。由于我们对相机的位置一无所知,不失一般性,可以将第一个相机设置在原点c0 = 0,并处于标准方向R0 = I。
在第一个图像中,在位置0和z距离处观察到的3D点p0 = d00

图11.11极线几何:向量st=c1-c0、p-c0和p-c1共面,并定义了以像素测量值x0和x1表示的基本极线约束。
d0通过变换映射到第二个图像中
d11 = p1 = Rp0 + t = R (d00) + t; (11.27)
其中j = Kj-1xj是(局部)射线方向向量。取两边的叉积(交换顺序),以消除右边的t,得到8
d1 [t]×1 = d0 [t]× R0 . (11.28)
两边与1取点积,得到
d0 ([t]× R)0 = d1 [t]×1 = 0; (11.29)
因为右边是一个具有两个相同元素的三重乘积。(另一种说法是,交叉乘积矩阵[t]×是斜对称的,并且当用同一个向量进行前乘和后乘时返回0。)
E 0 = 0; (11.30)
在哪里
E = [t]× R (11.31)
8交叉乘积算子[]×在(2.32)中被引入。
使光线0和1在三维空间中相交于点p,连接这两点的向量
相机中心c1−c0 =−R1t和对应于像素x0和x1的光线,即
(0 , R-11, −R-1t) = (R0 , 1, −t) = 1 · (t × R0 ) = ([t]× R)0 = 0. (11.32)
请注意,本质矩阵E将图像0中的点0映射到图像1中的直线l1=E0=[t]×R0,因为l1=0(图11.11)。所有这样的直线都必须穿过第二个极线e1,因此定义为E的左奇异向量,具有0的奇异值,或者等价地,向量t在图像1中的投影。这些关系的对偶(转置)给出了第一个图像中的极线l0 = ET 1和e0作为E的零值右奇异向量。
八点算法。鉴于这一基本关系(11.30),我们如何利用它来恢复编码在本质矩阵E中的相机运动?如果我们有N个对应的测量值{(xi0,xi1)},我们可以形成N个关于E的九个元素= {e00... e22 }的齐次方程,
| +xi1e02 | + | ||
| xi0yi1e00 +yi0yi1e11 xi0e20 +yi0e21 | +yi1e12 +e22 | + = 0 | (11.33) |
[xi1 x]⊗E = Zi⊗E = Zi·f = 0, (11.34)
其中⊗表示矩阵元素的逐元素乘法和求和,zi
f是Zi = i1和E矩阵的向量化形式。9给定N≥8如下
通过方程,我们可以使用SVD计算E中元素的估计值(在比例上)。
在存在噪声测量的情况下,这个估计值与统计最优有多接近?如果你查看(11.33)中的条目,可以看到有些条目是像xi0yi1这样的图像测量的乘积,而其他则是直接的图像测量(甚至是对角线)。如果测量的噪声相当,那么这些测量乘积项的噪声会被乘积中的另一个元素放大,这可能导致非常糟糕的缩放效果,例如,坐标较大的点(远离图像中心)的影响异常大。
9我们用f代替e来表示E的向量化形式,以避免与极点ej混淆。
为了抵消这一趋势,Hartley(1997a)建议将点坐标进行转换和缩放,使其质心位于原点,且其方差为1,即:
= s(xi—μx) (11.35)
i
=s(yi-μy) (11.36)
使得εi i = εi i=0~和ε
i +εi
= 2n,其中n是点数。10
一旦从变换坐标中计算出基本矩阵E
在(11.35–11.36)中进行尺度操作后,原始本质矩阵E可以恢复为
E = TT0 . (11.37)
在他的论文中,哈特利(1997a)将他提出的重新归一化策略与张(1998a,b)等人提出的其他距离度量方法的改进进行了比较,并得出结论,在大多数情况下,他的简单重新归一化方法与(或优于)替代技术一样有效。托尔和菲茨吉本(2004)推荐了该算法的一个变体,即E的上2×2子矩阵的范数设为1,并证明它在面对2D坐标变换时具有更好的稳定性。
7点算法。由于E是秩亏的,实际上我们只需要七个形式如公式(11.34)的对应关系来估计这个矩阵(Hartley1994a;Torr和Murray1997;Hartley和Zisserman2004)。在RANSAC稳健拟合阶段使用较少的对应关系的优势在于需要生成更少的随机样本。从这七个齐次方程组(我们可以将其堆叠成一个7×9矩阵用于SVD分析)中,可以找到两个独立向量,记为f0和f1,使得zi·fj = 0。这两个向量可以转换回3×3矩阵E0和E1,它们张成了解空间的基。
E = QE0 + (1 — Q)E1 . (11.38)
为了找到Q的正确值,我们观察到E的行列式为零,因为它秩不足,因此
j QE0 + (1 — Q)E1 j = 0. (11.39)
10更准确地说,Hartley(1997a)建议对点进行缩放,“使与原点的平均距离等于√2”,但单位方差的启发式方法计算速度更快(不需要对每个点进行平方根运算),并且应该产生可比的改进。
这给我们一个关于Q的三次方程,它有一个或三个解(根)。将这些值代入(11.38)以获得E,我们可以用这个基本矩阵与其他未使用的特征对应关系进行测试,以选择正确的那个。
归一化的“八点算法”(Hartley1997a)和上述描述的七点算法并不是估计相机运动的唯一方法。其他变体包括五点算法,该算法需要找到十阶多项式的根(Nist2004),以及处理特殊(受限)运动或场景结构的变体,这些将在本节后面讨论。由于这些算法使用较少的点来计算其估计值,因此在作为随机采样(RANSAC)策略的一部分时,对外部异常值的敏感度较低。11
恢复t和R。一旦获得了本质矩阵E的估计值,就可以估算出平移向量t的方向。请注意,无论使用多少相机或点,仅凭图像测量无法恢复两台相机之间的绝对距离。要确定最终的比例、位置和方向,总是需要关于相机和点的绝对位置或距离的知识,这在摄影测量中通常被称为地面控制点。
为了估计这个方向,观察到在理想的无噪声条件下,基本矩阵E是奇异的,即TE = 0。当对E进行SVD时,这种奇异性表现为一个0的奇异值,
× R =
UΣVT =
(11.40)
当从噪声测量中计算出E时,与最小奇异值相关的奇异向量给出了。(另外两个奇异值应该相似,但通常不等于1,因为E只是在未知尺度上计算的。)
一旦恢复了,我们如何估计相应的旋转矩阵R?回想一下,交叉乘积算子[]×(2.32)将一个向量投影到一组正交基向量上,包括,零出分量,并将另外两个向量旋转90°,
= s0×s1。根据公式(11.40和11.41),我们得到
E = [] × R = SZR90. STR = UΣVT ; (11.42)
由此我们可以得出结论,S = U。回想一下,对于一个无噪声的基本矩阵,(Σ = Z),因此
R90. UTR = VT (11.43)
R = UR. VT . (11.44)
不幸的是,我们只知道E和一个符号。此外,矩阵U和V
不能保证是旋转(你可以翻转它们的符号,仍然得到一个有效的SVD)。因此,我们必须生成所有四个可能的旋转矩阵
R = ±UR90. VT
(11.45)
并保留行列式jRj = 1的两个。为了区分剩余的一对潜在旋转,它们形成了一对扭曲的旋转(Hartley和Zisserman 2004,第259页),我们需要将它们与平移方向±的两种可能符号配对,并选择在两台相机前看到最多点数的组合。12
点必须位于相机前方,即沿从相机发出的视线方向处于正距离处,这一特性被称为手性(Hartley1998)。除了确定旋转和平移的符号外,如上所述,重建中点的手性(距离的符号)也可以用于RANSAC过程(连同重投影误差)来区分可能和不太可能的配置。13手性还可以用于将射影重建(第11.3.3节和第11.3.4节)转换为准仿射重建(Hartley1998)。
在某些情况下,专门设计的算法可以利用已知(或猜测)的摄像机布置或3D结构。
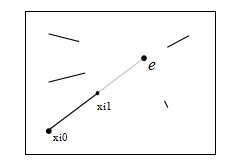
图11.12纯平移摄像机运动导致视觉运动,其中所有点都向(或远离)一个共同的扩展焦点(FOE)e移动。因此,它们满足三重乘积条件(x0,x1,e)= e·(x0×x1)= 0。
纯投影(已知旋转)。在已知旋转的情况下,我们可以预先旋转第二张图像中的点,以匹配第一张图像的观察方向。结果得到的三维点集都会朝向(或远离)扩展焦点(FOE),如图11.12.14所示。由此产生的本质矩阵E(在无噪声情况下)是对称的,因此可以通过设置eij =—eji和eii = 0来更直接地估计(11.33)。现在,两个具有非零视差的点就足以估计FOE。
通过最小化三重乘积,可以得到FOE估计值的更直接推导
(11.46)
(yi0 — yi1)e0 + (xi1 — xi0)e1 + (xi0yi1 — yi0xi1)e2 = 0. (11.47)
请注意,与八点算法一样,在计算该估计值之前,建议将二维点标准化为具有单位方差。
在有大量无穷远点可用的情况下,例如拍摄户外场景或相机运动相对于远处物体较小时,这提示了一种估计相机运动的替代RANSAC策略。首先,选择一对点来估计旋转,希望这两点都位于无穷远(非常远离相机)。然后,计算FOE并检查残差误差是否小(表明与该旋转假设一致),以及向或远离极点(FOE)的运动是否都在同一方向(忽略可能受噪声污染的微小运动)。
《星际迷航》和《星球大战》的粉丝们会认出这是“跃迁到超空间”的视觉效果。
纯旋转。纯旋转的情况会导致对本质的估计退化
矩阵E和变换方向。首先考虑旋转矩阵的情况
众所周知,FOE的估计值是退化的,因为xi0≈xi1,因此(11.47)也是退化的。类似的论证表明,本质矩阵的方程(11.33)也是秩亏的。
这表明,在计算完整的本质矩阵之前,可以先使用(8.32)计算旋转估计R,可能只需要少量的点,然后在继续进行完整的E计算之前旋转点,再计算残差。
主导平面结构。当场景中存在主导平面时,退化算法可以用来更可靠地恢复基础矩阵,而退化算法测试的是是否太多对应点共面(Chum、Werner和Matas 2005)。
正如你从前面的特殊情况可以看出,存在许多不同的两帧运动结构的专门案例以及许多合适的替代技术。Kneip和Furgale(2014)开发的OpenGV库包含了这些算法的开源实现。15
在许多情况下,比如尝试从互联网或未知相机拍摄的旧照片中构建3D模型时,这些照片没有任何EXIF标签,我们无法提前知道输入图像的固有校准参数。在这种情况下,我们可以静态地估计两帧重建,尽管真实的度量结构可能不可用,例如,世界中的正交线或平面最终可能不会被重建为正交。
考虑我们用来估计基本矩阵E(11.30–11.32)的推导。在未校准的情况下,我们不知道校准矩阵Kj,因此我们不能使用正态-
射线方向为j = Kj-1xj。相反,我们只能访问图像坐标xj,
因此,基本矩阵方程(11.30)变为
E1 = xK TEK0-1x0 = xFx0 = 0; (11.48)
F = K TEK0-1
(11.49)
称为基本矩阵(Faugeras1992;Hartley、Gupta和Chang1992;Hartley和Zisserman2004)。
与基本矩阵一样,基本矩阵(原则上)是秩为2的,
(11.50)
其最小的左奇异向量表示图像1中的epipolee1,而其最小的右奇异向量是e0(图11.11)。基本矩阵可以分解为一个斜对称交叉乘积矩阵[e]×和一个单应H,
F = [e]× . (11.51)
从(11.49)式原则上讲,同态应等于
= K TRK0—1 ; (11.52)
不能从F中唯一恢复,因为任何形式为/ = + evT的同态结果
在同一个F矩阵中。(注意,[e]×会湮灭e的任何倍数。)
这些有效的单应性变换H中的任何一个都映射了场景中的一张图像到另一张图像中的某个平面。如果不选择四个或更多共面对应点来计算H(类似于猜测E的旋转方式),或者通过H映射一张图像中的所有点并查看哪些点与另一张图像中的相应位置对齐,就无法提前判断是哪一个。这种表示通常被称为平面加视差(Kumar、Anandan和Hanna 1994;Sawhney 1994),并在Section2.1.4中进行了更详细的描述。
~为了创建场景的投影重建,我们可以选择任何满足方程(11.49)的有效单应矩阵H。例如,采用类似于方程(11.40–11.44)的技术,我们得到
F = [e]× = SZR90. ST = UΣVT (11.53)
因此 ~
H = UR. VT ; (11.54)其中,最小值的奇异值矩阵被合理的替代值(比如中间值)所取代。16然后我们可以形成一对相机矩阵
16 Hartley和Zisserman(2004,第256页)建议使用=[e]×F(Luong和Vi ville1996
),该方法可将
飞机上的摄像头在无穷远处。
712 计算机视觉:算法和应用,第2版(最终稿,2021年9月)
由此可以使用三角测量法计算场景的投影重建(第11.2.4节)。
虽然投影重建本身可能没有用处,但通常可以升级为仿射或度量重建,如下所述。即使不进行这一步骤,基础矩阵F在寻找额外对应点时仍然非常有用,因为所有这些对应点都必须位于相应的极线上,即图像0中的任何特征x0都必须在其对应的图像1中的极线l1 = Fx0上,假设
11.3.4自校准
结构从运动计算的结果如果能获得度量重建会更有用,即平行线保持平行,正交墙面保持垂直,重建模型是现实的缩放版本。多年来,已经开发了大量自校准(或自动校准)技术,用于将投影重建转换为度量重建,这相当于恢复与每张图像相关的未知校准矩阵Kj(Hartley和Zisserman 2004;Moons、Van Gool和Vergauwen 2010)。
在已知场景附加信息的情况下,可以采用不同的方法。例如,如果场景中有平行线,可以利用三个或更多消失点来建立无穷远平面的单应性,从而恢复焦距和旋转。如果观察到了两个或多个有限正交消失点,则可以使用基于消失点的单图像校准方法(第11.1.1节)。
在缺乏此类外部信息的情况下,仅凭对应关系无法恢复每个图像的完全参数化的独立校准矩阵Kj。为了理解这一点,考虑所有相机矩阵Pj = Kj [Rj jtj ]将世界坐标pi =(Xi,Yi,Zi,Wi)投影到屏幕坐标xij ~ Pj pi的集合。现在再考虑通过任意4×4投影变换H~转换三维场景{pi },得到一个新的模型,其中点pi=Hpi。将每个Pj矩阵后乘以H-1仍然会产生相同的屏幕坐标,并且可以通过对新的相机矩阵Pj=Pj H-1应用RQ分解来计算新的校准矩阵集。
因此,所有自校准方法都假设校准矩阵具有某种受限形式,要么通过设置或等同某些元素,要么假设这些元素不会随时间变化。尽管哈特利和齐瑟曼(2004);穆恩斯、范古尔和维尔高文(2010)讨论的大多数技术需要三个或更多的帧,在本节中我们介绍一种简单的方法,可以从两个图像中恢复焦距(f0,f1)。
在两帧重建中,基本矩阵F(Hartley和Zisserman,2004年,第472页)。
为了实现这一目标,我们假设相机的偏斜度为零,已知的纵横比(通常设为1),以及已知的图像中心,如公式(2.59)所示。这个假设在实践中有多合理?答案是“视情况而定”。
如果需要绝对的测量精度,如摄影测量应用中那样,必须使用第11.1节中的某项技术预先校准相机,并利用地面控制点来确定重建。相反,如果我们只是希望为可视化或基于图像的渲染应用重建世界,例如斯纳维利、塞茨和舍利斯基(2006)提出的“照片旅游”系统,这种假设在实际操作中是相当合理的。
如今大多数相机的像素呈方形,图像中心位于画面中央附近,由于径向畸变(第11.1.4节),这些相机更可能偏离简单的相机模型,因此应尽可能进行补偿。最大的问题出现在图像被裁剪偏移中心时,此时图像中心将不再居中;或者当拍摄的是不同视角的照片时,就需要使用通用相机矩阵。17
考虑到这些注意事项,基于克鲁帕方程的两帧焦距估计算法(由哈特利和齐瑟曼于2004年提出,第456页)的具体步骤如下。取基础矩阵F(11.50)的左奇异向量{u0,u1,v0,v1 }及其对应的奇异值{σ0,σ 1 },并形成以下方程组:
(11.56)
两个矩阵在哪里
Dj = KjK = diag
eij0(f) = uD0 uj = aij + bij f , (11.58)
eij1(f) = σi σj vD1 vj = cij + dij f. (11.59)
请注意,每一个都是f或f的仿射(线性加常数)函数。因此,我们可以
将这些方程交叉相乘,得到关于f的二次方程,可以很容易地得到
在“照片旅游”中,我们的系统注册了巴黎圣母院外的信息标志的照片和大教堂的真实照片。
已解决。(另见Bougnoux(1998)和Kanatani与Matsunaga(2000)的其他表述。)
另一种解决方案是观察到我们有一组由未知标量λ相关的三个方程,即,
eij0(f) = λeij1(f) (11.60)
(Richard Hartley,个人交流,2009年7月)。这些都可以很容易地解决,得到
(f;λf;λ)因此(f0;f1)。
这种方法在实际应用中效果如何?存在某些退化配置,例如没有旋转或光轴相交时,该方法根本不起作用。(在这种情况下,可以通过改变相机的焦距来获得更深或更浅的重建,这是浮雕模糊的一个例子(第11.4.5节)。)哈特利和齐瑟曼(2004)建议使用基于三重技术的方法。
或者更多的帧。但是,如果您发现两个图像,它们的估计值为(f;λf;λ)
条件良好时,可以用来初始化所有参数的更完整的束调整(第11.4.2节)。另一种方法,在如照片旅游系统中常用,是使用相机EXIF标签或通用默认值来初始化焦距估计,并在束调整过程中对其进行优化。
基本的两帧结构从运动中的一种有趣的应用是视图变形(也称为视图插值,参见第14.1节),它可以用于从3D场景的一个视图生成另一个视图的平滑3D动画(Chen和Williams1993;Seitz和Dyer 1996)。
要实现这样的过渡,首先需要平滑地插值相机矩阵,即相机的位置、方向和焦距。虽然可以使用简单的线性插值(将旋转表示为四元数(第2.1.3节)),但通过缓入缓出相机参数,例如使用升余弦函数,以及沿更圆的轨迹移动相机(Snavely,Seitz,和Szeliski 2006),可以获得更加悦目的效果。
为了生成中间帧,要么需要建立完整的3D对应关系(第12.3节),要么为每个参考视图创建3D模型(代理)。第14.1节描述了几种广泛使用的方法来解决这个问题。最简单的方法之一是仅对每张图像中匹配的特征点进行三角化,例如使用德劳内三角化。当3D点重新投影到它们的中间视图时,可以使用仿射或投影映射将像素从原始源图像映射到新的视图(Szeliski和Shum 1997)。最终图像则通过线性混合合成。

图11.13使用因子分解法对旋转乒乓球进行三维重建(Tomasi
(Kanade1992)©1992 Springer:(a)叠加了跟踪特征的样本图像;(b)子采样特征运动流;(c)重建的3D模型的两个视图。
两个参考图像,与通常的变形(第3.6.3节)一样。
11.4 从运动中提取多帧结构
虽然两帧技术对于从立体图像对中重建稀疏几何结构和初始化更大规模的三维重建是有用的,但大多数应用可以从通常在场景的照片集合和视频中可用的大量图像中受益。
在本节中,我们简要回顾一种较老的技术,称为分解,它可以为短视频序列提供有用的解决方案,然后转向更常用的束调整方法,该方法使用非线性最小二乘法在一般相机配置下获得最优解。
11.4.1因式分解
在处理视频序列时,我们经常从视频中获得扩展特征轨迹(Section7.1.5)
使用一个叫做分解的过程可以恢复结构和运动。
考虑一个旋转的乒乓球产生的轨迹,它被标记了点以使其形状和运动更易辨认(图11.13)。我们很容易从轨迹的形状看出移动物体必须是一个球体,但是我们如何从数学上推断这一点呢?
结果表明,在下面讨论的正字法或相关模型下,形状和运动可以同时使用奇异值分解(Tomasi和
Kanade1992)。如何做到这一点的细节在Tomasi和Kanade的论文中有所介绍
(1992)以及本书第一版(Szeliski2010,第7.3节)。
一旦旋转矩阵和三维点位置被恢复,仍然存在一种浮雕式的不确定性,即我们无法确定物体是向左旋转还是向右旋转,或者其深度反转版本是否在相反方向移动。(这可以从经典的旋转内克立方体视觉错觉中看出。)额外的线索,如点的出现和消失,或透视效果,这些将在下文讨论,可以用来消除这种不确定性。
对于纯正字法以外的运动模型,例如比例正字法或准透视法,上述方法必须以适当的方式扩展。这些技术从基本原理推导相对简单;更多细节可以在扩展基本分解方法到这些更灵活模型的论文中找到(Poel- man和Kanade 1997)。原始分解算法的其他扩展包括多体刚体运动(Coste-ra和Kanade 1995)、分解的顺序更新(Morita和Kanade 1997)、添加直线和平面(Morris和Kanade 1998),以及重新缩放测量值以纳入个体位置不确定性(Anandan和Irani 2002)。
因子分解方法的一个缺点是需要完整的轨迹集,即每个点必须在每一帧中可见,才能使因子分解方法生效。Tomasi和Kanade(1992)通过首先将因子分解应用于较小且更密集的子集,然后利用已知的相机(运动)或点(结构)估计来推测额外的缺失值,从而逐步纳入更多特征和相机。Huynh、Hartley和Heyden(2003)将这种方法扩展到视图缺失数据作为异常值的特殊情况。Buchanan和Fitzgibbon(2005)开发了快速迭代算法,用于处理带有缺失数据的大矩阵因子分解。主成分分析(PCA)在处理缺失数据时的一般主题也出现在其他计算机视觉问题中(Shum、Ikeuchi和Reddy 1995;De la Torre和Black 2003;Gross、Matthews和Baker 2006;Torresani、Hertzmann和Bregler 2008;Vidal、Ma和Sastry 2016)。
视角与投影分解
常规分解的另一个缺点是无法处理透视相机。解决这一问题的一种方法是先进行初始仿射(例如正交)重建,然后通过迭代方式校正透视效果(Christy和Horaud 1996)。该算法通常在三到五次迭代中收敛,大部分时间用于奇异值分解计算。
另一种方法,不假设部分校准的相机(已知的im
(中心点、方像素和零偏斜)是执行完全投影分解(Sturm和Triggs1996;Triggs1996)。在这种情况下,将相机矩阵的第三行包含在测量矩阵中相当于将每个重建的测量值相乘。
xji = Mj pi的逆(投影)深度ηji = dj1 = 1/(Pj2pi),或者等效地,多-
将每个测量位置乘以其投影深度dji。在Sturm和Triggs(1996)的原始论文中,投影深度dji是从两帧重建中获得的,而在后来的工作中(Triggs 1996;Oliensis和Hartley 2007),它们被初始化为dji = 1,并在每次迭代后更新。Oliensis和Hartley(2007)提出了一种保证收敛到固定点的更新公式。这些作者都没有建议实际估计Pj的第三行作为投影深度计算的一部分。无论如何,当完全投影重建比部分校准重建更优时,尤其是在用于初始化所有参数的完整束调整时,这一点尚不清楚。
因子分解方法的一个吸引点在于它们提供了一种“封闭形式”(有时称为“线性”)的方法来初始化诸如束调整等迭代技术。另一种初始化技术是估计所有相机共有的平面对应的单应矩阵(Rother和Carlsson 2002)。在已校准的相机设置中,这可以对应于估计所有相机的一致旋转,例如使用匹配的消失点(Antone和Teller 2002)。一旦这些参数被恢复,就可以通过求解线性系统来获得相机位置(Antone和Teller 2002;Rother和Carlsson 2002;Rother 2003)。
正如我们之前多次提到的,恢复结构和运动最准确的方法是进行测量(重投影)误差的稳健非线性最小化,这在摄影测量学(以及现在的计算机视觉)领域通常被称为束调整。Triggs、McLauchlan等人(1999)对此主题提供了极好的概述,包括其历史发展、摄影测量文献的引用(Slama 1980;Atkinson 1996;Kraus 1997),以及度量模棱两可的微妙问题。这一主题也在多视图几何的教科书和综述中得到了深入探讨(Faugeras和Luong 2001;Hartley和Zisserman 2004;Moons、Van Gool和Vergauwen 2010)。
在我们对束调整的讨论中,我们已经介绍了束调整的要素
推断姿态估计(第11.2.2节),即公式(11.14–11.20)和图11.7。

图11.14一组链式变换,用于通过一系列变换f(k)将3D点pi投影到2D测量值xij上,每个变换由其自身的参数集控制。虚线表示在反向传播过程中计算偏导数时的信息流。径向畸变函数的公式为fRD (x) =(1 + h1 r²+ h2 r⁴)x。
这些公式和完整的束调整之间的最大区别是,我们的特征位置测量xij现在不仅取决于点(轨迹)索引i,而且还取决于相机姿态索引j,
xij = f (pi, Rj, cj, Kj ), (11.61)
并且三维点位置pi也在同时更新。此外,通常会增加一个径向畸变参数估计阶段(2.78),
fRD (x) = (1 + h1 r2 + h2 r4 )x, (11.62)
如果所用摄像机未进行预校准,如图11.14所示。
虽然图11.14中的大多数框(变换)之前已经解释过(11.19),但最左边的框还没有。这个框执行预测和测量的二维位置ij Σij的稳健比较。更详细地说,这个操作可以写为
rij = ij - ij ,
(11.63)
sj = rΣi1 rij , (11.64)
eij = (sj ), (11.65)其中(r2)= P(r)。相应的雅可比矩阵(偏导数)可以写为
(11.66)
1 rij
. (11.67)

图11.15摄像机支架及其相关的变换链。(a)作为移动支架(机器人)
在世界中移动,它相对于时间t的世界的姿态由(R;c)捕捉。
每个摄像机相对于支架的姿态由(R;c)捕捉。(b)一个具有世界坐标系的三维点
坐标p首先转换为rig坐标p,然后通过其余的
如图11.14所示,为特定相机的链。
上述链式表示的优势不仅在于简化了偏导数和雅可比矩阵的计算,还能适应任何相机配置。例如,考虑图11.15a中展示的一对安装在机器人上的相机,该机器人正在世界中移动。通过将图11.14中最右侧的两个变换替换为图11.15b所示的变换,我们可以同时恢复机器人在每个时间点的位置以及每台相机相对于整个装置的校准,此外还能获得世界的三维结构。
大规模束调整问题,例如从数千张互联网照片中重建三维场景(Snavely,Seitz和Szeliski 2008b;Agarwal,Furukawa等2010,2011;Snavely,Simon等2010),可能需要解决包含数百万测量值(特征匹配)和数万个未知参数(三维点位置和相机姿态)的非线性最小二乘问题。如果不加以谨慎处理,这类问题可能会导致严重的后果。

图11.16 (a)玩具结构运动问题的二部图及其相关的雅可比矩阵J和(c)海森矩阵A。数字表示三维点,字母表示相机。虚线弧和浅蓝色方块表示当结构(点)变量被消除时发生的填充。
问题可能变得难以解决,因为稠密最小二乘问题的(直接)解与未知数的数量呈立方关系。
幸运的是,运动结构问题是一个关于结构和运动的二元问题。给定图像中的每个特征点xij都依赖于一个三维点位置pi和一个三维相机姿态(Rj;cj)。这在图11.16a中有所说明,其中每个圆圈(1-9)表示一个三维点,每个方块(A-D)表示一个相机,线条(边)表示哪些点在哪些相机中可见(二维特征)。如果所有点的值已知或固定,则所有相机的方程变得独立,反之亦然。
如果我们先在海森矩阵A(以及右侧向量b)中排列结构变量,再排列运动变量,则得到如图11.16c.19所示的海森结构。当使用稀疏乔列斯基分解求解此类系统时(见附录A.4)(Bj rck1996;Golub和Van Loan1996),填充会在较小的运动海森矩阵Acc中发生(Szeliski
和Kang1994;Triggs、McLauchlan等人1999;Hartley和Zisserman2004;Lourakis和Argyros2009;Engels、Stew nius和Nist r2006)。最近的一些论文(Byr d和A˚str m2009;Jeong、Nist r等人
2010;Agarwal、Snavely等人2010;Jeong
、Nist r等人2012)探讨
了使用迭代(共轭梯度)技术解决束调整问题的
方法。其他论文则研究了并行多核算法的使用(Wu、Agarwal等人2011)。
19当摄像机数量少于3D点时,这种排序方式是可取的,这是通常的情况。例外情况是,我们通过许多视频帧跟踪少量点,在这种情况下,应该反向这种排序方式。
更详细地说,使用Schur补计算降阶运动Hessian矩阵,
= ACC
- AAP-Apc; (11.68)
其中,APP是点(结构)海森矩阵(图11.16c的左上角块),APC是点-相机海森矩阵(右上角块),而ACC和A分别是点变量消除前后
的运动海森矩阵(图11.16c的右下角块)。请注意,如果两个相机看到相同的三维点,则A在这两个相机之间
有一个非零元素。这在图11.16a中用虚线弧表示,在图11.16c中用浅蓝色方块表示。
在重建算法中,如果存在全局参数,例如所有相机共有的相机内参,或者如图11.15所示的相机支架校准参数,则应将其放在最后(放置在A的右边缘和底部边缘),以减少填充。
恩格斯、斯图尼乌斯和尼斯特(
2006)提供了一种稀疏束调整的优良配方,包括初始化迭代所需的所有步骤,以及在实时设置中使用固定数量的后向帧系统的典型计算时间。他们还建议使用齐次坐标来表示结构参数pi,这是一个好主意,因为它可以避免接近无穷远点的数值不稳定问题。
束调整现在是大多数基于运动构建结构问题的标准方法,常用于处理包含数百张弱校准图像和数万个点的问题。(更大规模的问题通常在摄影测量和航空影像中解决,但这些问题通常经过精心校准,并利用了地面控制点。)然而,随着问题规模的增大,每次迭代重新求解完整的束调整变得不切实际。
处理这一问题的一种方法是使用增量算法,随着时间的推移逐步增加新的摄像头。(如果数据来自视频摄像机或移动车辆,则这种方法尤为适用(Nist r、Naroditsky和Bergen 2006;Pollefeys、Nist r等2008)。)可以使用卡尔曼滤波器
来随着新信息的获取而
逐步更新估计值。然而,这种顺序更新仅在统计上对线性最小二乘问题是最优的。
对于非线性问题,如运动中的结构问题,需要使用扩展卡尔曼滤波器(Gelb1974;Vi ville和Faugeras1990)。为了克服这一限制,可以对数据进行多次处理(Azarbayejani和Pentland1995)。由于点会从视图
中消失(旧相机变得无关紧要),可以使用可变状态维度滤波器(VSDF)来调整随时间变化的状态变量集,例如,仅保留最近k帧中看到的相机和点轨迹(McLauchlan2000)。一种更灵活的方法是使用
固定数量的帧用于通过点和相机向后传播校正,直到参数变化低于阈值(Steedly和Essa 2001)。这些技术的变体,包括使用固定窗口进行束调整的方法(Engels、Stew nius和Nist r 2006)或选择关键帧进行完整的束调整(Klein和Murray 2008),现在常用于同时定位与建图(SLAM)和增强现实
应用中,详见第11.5节。
当需要最高精度时,仍然最好对所有帧进行全面束调整。为了控制由此产生的计算复杂度,一种方法是将帧子集锁定为局部刚性配置,并优化这些簇的相对位置(Steedly,Essa和Dellaert 2003)。另一种方法是从较小数量的帧中选择一组骨架集,该集合仍能覆盖整个数据集并产生具有相当精度的重建(Snavely,Seitz和Szeliski 2008b)。我们在第11.4.6节中更详细地描述了后一种技术,在那里我们讨论了结构从运动到大型图像集的应用。关于高效解决大型结构从运动和SLAM系统的其他技术,可以在Dellaert和Kaess(2017);Dellaert(2021)的综述中找到。
虽然束调整和其他稳健的非线性最小二乘技术是大多数结构从运动问题的首选方法,但它们存在初始化问题,即如果初始条件不够接近全局最优解,可能会陷入局部能量最小值。许多系统试图通过在早期重建时保守处理以及选择哪些相机和点加入解决方案来减轻这一问题(第11.4.6节)。然而,另一种替代方案是重新定义问题,使用支持计算全局最优解的范数。
卡赫和哈特利(2008)描述了在几何重建问题中使用L∞范数的技术。这类范数的优势在于,可以利用二阶锥规划(SOCP)高效计算全局最优解。然而,L∞范数对异常值特别敏感,因此在使用前必须结合良好的异常值剔除技术。
大量高质量的开源束调整包已经开发出来,包括Ceres求解器、多核束调整(吴、阿加瓦尔等人,2011年)、基于稀疏莱文堡-马夸特法的非线性最小二乘优化器和束调整器,以及OpenSfM。您可以在附录C.2中找到更多关于开源软件的指南,以及对开源和商业摄影测量软件的综述。
结构从运动的一个最精妙的应用是估计视频或电影摄像机的三维运动,以及三维场景的几何形状,以便将三维图形或计算机生成图像(CGI)叠加到场景上。在视觉效果行业中,这被称为匹配移动问题(Roble1999),因为用于渲染图形的合成三维摄像机的运动必须与现实世界的摄像机运动相匹配。对于非常小的运动,或者仅涉及纯旋转的运动,一两个跟踪点就足以计算所需的视觉运动。对于在三维空间中移动的平面表面,则需要四个点来计算单应性,然后可以使用该单应性插入平面覆盖层,例如,在体育赛事期间替换广告牌的内容。
这个问题的一般版本需要估计完整的三维相机姿态以及镜头的焦距(变焦)和可能的径向畸变参数(Roble1999)。当场景的三维结构事先已知时,可以使用诸如视图相关性(Bogart1991)或透镜内相机控制(Gleicher和Witkin1992)等姿态估计技术,如Section11.4.4所述。
对于更复杂的场景,通常最好使用结构从运动技术同时恢复相机运动和三维结构。使用这些技术的关键在于,为了防止合成图形与实际场景之间出现任何可见的抖动,特征必须被跟踪到非常高的精度,并且在插入位置附近必须有足够的特征轨迹。当今一些最知名的匹配移动软件包,如2d3公司的boujou软件包,该软件包于2002年获得艾美奖,起源于计算机视觉社区中的结构从运动研究(Fitzgibbon和Zisserman 1998)。
因为运动结构涉及估计大量高度耦合的参数,通常没有已知的“真实”成分,所以运动结构算法产生的估计结果往往表现出大量的不确定性(Szeliski和Kang 1997;Wilson和Wehrwein 2020)。一个例子是经典的浮雕模糊性问题,
使得很难同时估计场景的三维深度和相机运动量(Oliensis2005).26
如前所述,仅凭单目视觉测量无法恢复重建场景的独特坐标系和比例。(当使用立体相机时,如果我们知道相机之间的距离(基线),则可以恢复比例。)这种七自由度(坐标系和比例)的量纲不确定性使得计算与三维重建相关的协方差矩阵变得复杂(Triggs,McLauchlan等1999;Kanatani和Morris 2001)。一种简单的方法是忽略量纲自由度(不确定性),即丢弃信息矩阵(逆协方差)的七个最小特征值,这些值在噪声缩放下等同于问题的海森矩阵A(见第8.1.4节和附录B.6)。完成这一步后,可以对所得矩阵求逆以获得参数协方差的估计。
斯泽利斯基和康(1997)利用这种方法来可视化典型结构从运动问题中最大的变化方向。不出所料,他们发现,在忽略规范自由度的情况下,对于从少量附近视角观察物体等问题,最大的不确定性在于三维结构的深度,而非相机运动的程度。27
也可以估计单个参数的局部或边缘不确定性,这相当于从完整的协方差矩阵中提取块子矩阵。在某些条件下,例如当相机姿态相对于3D点位置较为确定时,这种不确定性估计是有意义的。然而,在许多情况下,单个不确定性度量可能会掩盖重建误差的相关程度,因此查看最大联合变异的前几个模式是有帮助的。
另一种方式是,规范不确定性会影响运动结构,特别是束调整,使系统中的海森矩阵A秩亏,因此无法求逆。为了缓解这一问题,已经提出了一些技术(Triggs,McLauchlan等,1999;Bartoli,2003)。然而,在实际应用中,通常的做法是简单地将Hessian对角线λdiag(A)的小部分加到Hessian矩阵A本身上,这在Levenberg-Marquardt非线性最小二乘算法中有所体现(附录A.3)。
26浮雕是指一种雕塑形式,其中物体通常位于装饰性的浮雕上,雕刻得比实际占据的空间要浅。当从上方被阳光照亮时,由于相对深度与光源角度之间的模糊性(第13.1.1节),它们看起来具有真正的三维深度。
27一种减少此类模糊性的有效方法是使用广角摄像机(Antone和Teller 2002;Levin和Szeliski 2006)。

图11.17增量结构从运动中获得(Snavely、Seitz和Szeliski2006)©2006 ACM。从特雷维喷泉的初始两帧重建开始,使用姿态估计添加图像批次,并使用束调整优化它们的位置(以及3D模型)。
结构从运动最广泛的应用是在视频序列和图像集合中重建三维物体和场景(Pollefeys和Van Gool 2002)。过去二十年间,自动执行此任务的技术出现了爆炸式增长,无需任何手动对应或预先勘测的地面控制点。许多这些技术假设场景是由同一台相机拍摄的,因此所有图像都具有相同的内参(Fitzgibbon和Zisserman 1998;Koch、Pollefeys和Van Gool 2000;Schaffalitzky和Zisserman 2002;Tuytelaars和Van Gool 2004;Pollefeys、Nist等2008;Moons、Van Gool和Vergauwen 2010)。许多这些技术利用稀疏特征匹配和结构从运动计算的结果,然后使用多视图立体技术计算密集
的三维表面模型(第12.7节)(Koch、Pollefeys和Van Gool 2000;Pollefeys和Van Gool 2002;Pollefeys、Nist等2008;Moons、Van Gool和Vergauwen 2010;Schnberger、Zheng等2016)。
在这个领域的一项令人兴奋的创新是将运动结构和多视图立体技术应用于从互联网获取的数千张图像,而这些照片拍摄相机的信息知之甚少(Snavely,Seitz和Szeliski 2008a)。在开始运动结构计算之前,首先需要建立不同图像对之间的稀疏对应关系,然后将这些对应关系链接成特征轨迹,即关联单个二维图像特征与全局三维点。由于所有图像对的O(N^2)比较过程可能非常缓慢,因此识别社区开发了多种技术来加快这一过程(第7.1.4节)(Nist和Stew nius 2006;Philbin、Chum等2008;Li、Wu等2008;Chum、Philbin和Zisserman 2008;Chum和Matas 2010a;Arandjelovi和Zisserman 2012)。

图11.18由斯纳维利、塞茨和塞尔利斯基(2006)开发的增量结构从运动算法生成的3D重建©2006 ACM:特拉法加广场的(a)相机和点云;长城上的(b)相机和点叠加在图像上;布拉格老城广场的(c)俯视图,该重建与航拍照片注册。
开始重建过程时,选择一对好的图像至关重要,这些图像不仅包含大量一致的匹配点(以降低错误对应的可能性),还应有显著的面外视差,以确保能够获得稳定的重建结果(Snavely,Seitz和Szeliski 2006)。与照片相关的EXIF标签可用于获取相机焦距的良好初始估计,尽管这并非总是严格必要,因为这些参数会在束调整过程中重新调整。
一旦初始对被重建,就可以估计出看到足够多结果3D点的相机姿态(第11.2节),并使用完整的相机和特征对应关系进行另一轮束调整。图11.17展示了增量束调整算法的进展过程,在每一轮束调整后都会增加一组相机,而图11.18则展示了一些额外的结果。这种种子和生长方法的替代方案是首先重建图像三元组,然后将它们层次化合并成更大的集合(Fitzgibbon和Zisserman 1998)。
不幸的是,随着增量结构从运动算法不断增加更多的摄像头和点,它可能会变得极其缓慢。直接求解相机姿态更新的密集O(N)方程组可能需要O(N^3)的时间;而结构从运动问题很少是密集的,像城市广场这样的场景具有较高的比例。
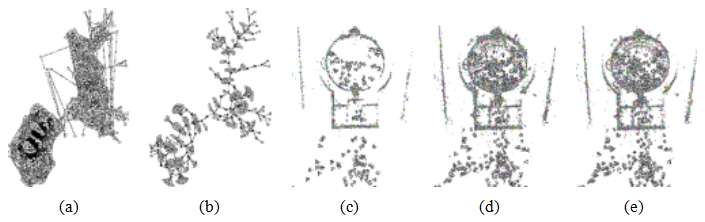
图11.19使用骨架集进行大规模结构运动重建(Snavely,Seitz和Szeliski 2008b)©2008 IEEE:784张图像的原始匹配图;(b)包含101张图像的骨架集;(c)从骨架集中重建的场景(万神殿)俯视图;(d)添加剩余图像后通过姿态估计重建的结果;(e)最终束调整重建,几乎完全相同。
相机识别出共同点。每次增加几台相机后重新运行束调整算法,会导致运行时间随着数据集中图像数量的增加而呈四次方增长。解决这一问题的一种方法是选择较少的图像进行原始场景重建,并在最后再加入剩余的图像。
斯纳维利、塞茨和谢利斯基(2008b)开发了一种算法,用于计算这样的图像骨架集,该算法保证生成的重建误差在最优重建精度的有界因子内。他们的算法首先评估所有重叠图像之间的两两不确定性(位置协方差),然后将这些不确定性串联起来,以估计任意远距离对的相对不确定性的下限。骨架集构建的方式是,任意一对之间的最大不确定性增长不超过一个常数因子。图11.19展示了为罗马万神殿的784张图像计算出的骨架集的一个例子。如你所见,尽管骨架集仅包含原始图像的一小部分,但骨架集和完整的束调整重建的形状几乎无法区分。
自斯纳维利、塞茨和舍利斯基(2008a,b)首次发表大规模互联网照片重建研究以来,大量后续论文探索了更大的数据集和更高效的算法(阿加瓦尔、古川等人2010,2011;弗拉姆、菲特-格奥格尔等人2010;吴2013;海因利、施恩伯格等人2015;施恩伯格和弗拉姆2016)。其中,COLMAP开源结构从运动和多
视图立体系统目前是最广泛
使用的之一,因为它能够重建极其庞大的场景,

图11.20大规模重建,使用COLMAP结构从运动和多视图立体系统创建:从21K构建的罗马市中心(a)稀疏模型
照片(Sch nberger和Frahm2016)©2016 IEEE;多个地标的(b)密集模型
采用MVS管道生产(Sch nberger,Zheng等人,2016)©2016 Springer。
例如图11.20所示(Sch nberger和Frahm2016).29
从大量非结构化图像集合中自动重建三维模型的能力,也揭示了传统运动结构算法中存在的细微问题,包括需要处理重复和相似的结构(吴、弗拉姆和波莱菲斯2010;罗伯茨、辛哈等人2011;威尔逊和斯纳维利2013;海因利、邓恩和弗拉姆2014),以及动态视觉对象如人物(吉、邓恩和弗拉姆2014;郑、王等人2014)。这一能力还开启了多种附加应用,包括自动查找和标注感兴趣的位置和区域(西蒙、斯纳维利和塞茨2007;西蒙和塞茨2008;加米特、博萨德等人2009),以及对大型图像集合进行聚类以便自动标注(李、吴等人2008;夸克、莱贝和范古尔2008)。关于基于图像渲染的一些其他应用将在第14.1.2节中详细讨论。
尽管增量束调整算法仍然是大规模重建中最常用的方法(Sch nberger和Frahm2016),但它们可能相当慢,因为

图11.21 Sinha、Steedly和Szeliski(2010)提出的全局运动结构流水线©2010斯普林格。首先使用消失点和基于特征的成对旋转估计来确定一组全局一致的方向(旋转)。然后通过单次线性最小二乘法最小化,估计所有成对重建的尺度以及相机中心位置。
需要连续解决越来越大的优化问题。在特征对应关系建立后,一种替代迭代增长解决方案的方法是在一个全局步骤中求解所有结构和运动未知数。
一种方法是建立一个线性方程组,将所有相机中心以及三维点、线和平面方程与已知的二维特征或线条位置联系起来(Kaucic,Hartley和Dano 2001;Rother 2003)。然而,这些方法需要参考平面(例如,建筑物墙壁)在所有图像中都可见且匹配,并且对远距离点敏感,这些点必须首先被剔除。尽管这些方法理论上很有吸引力,但并未广泛使用。
第二种方法由戈文杜(2001)首次提出,首先使用第11.3.3节讨论的技术计算成对欧几里得结构和运动重建。然后利用成对旋转估计来计算每个相机的全局一致方向估计,这一过程称为旋转平均(戈文杜2001;马蒂内克和帕伊德拉2007;查特吉和戈文杜2013;哈特利、特鲁姆夫等人2013;德拉尔特、罗森等人2020)。最后一步是通过将每个局部相机平移缩放至全局坐标系中,确定相机位置(戈文杜2001,2004;马蒂内克和帕伊德拉2007;辛哈、斯特迪和舍利斯基2010)。在机器人(SLAM)领域,这最后一步被称为姿态图优化(卡尔洛内、特隆等人2015)。
图11.21展示了一个更近期的实现该概念的流水线,包括初始特征点提取、匹配和双视图重建,随后是全局旋转估计,最后求解相机中心。辛哈、斯特迪和斯泽利斯基(2010)开发的流水线还匹配了消失点,当这些消失点可以找到时,
以消除全球方向估计中的旋转漂移。
虽然有几种替代算法可以估计全局旋转,但估计相机中心的算法种类更多。在对所有相机进行全局旋转估计后,我们可以计算全局定向的局部平移
在每个重构的对ij中,用ij表示这个方向。基本关系
未知摄像机中心{ci }和平移方向之间的关系可以表示为
cj - ci = sij ij (11.69)
或
ij × (cj - ci) = 0 (11.70)
(Govindu2001)。第一组方程可以求解以获得相机中心{ci }和尺度变量sij,而第二组方程则直接生成相机位置。除了具有齐次性(仅知其比例)外,相机中心还具有平移自由度,即它们都可以被平移(但在运动结构中这总是成立的)。
因为这些方程最小化了局部平移方向与全局相机中心差异之间的代数对齐,所以它们无法正确地权衡不同基线的重建结果。为了纠正这一问题,已经提出了几种替代方案(Govindu 2004;Sinha、Stedly和Szeliski 2010;Jiang、Cui和Tan 2013;Moulon、Monasse和
Marlet2013;Wilson和Snavely2014;Cui和Tan2015;zyes¸il和Singer2015;Holyn-
ski、Geraghty等人,2020年)。其中一些技术也无法处理共线相机,正如最初的形式一样,以及一些更近期的技术,我们可以沿着共线段移动相机,仍然满足方向约束。
对于在大型区域如广场上拍摄的社区照片集,这并不是一个关键问题(Wilson和Snavely 2014)。然而,在从视频重建或在建筑物内行走时,共线相机问题确实是一个实际问题。Sinha、Steedy和Szeliski(2010)通过估计共享同一相机的两两重建之间的相对尺度来解决这一问题,然后利用这些相对尺度约束所有全局尺度。
包含这些全局技术的一些开源结构化运动管道有Theia32(Sweeney,Hollerer和Turk2015)和OpenMVG33 (Moulon,Monasse

图11.22玩具房屋的两个图像及其匹配的3D线段(Schmid和Zisserman1997)©1997 Springer。
最通用的运动结构算法在重建对象或场景时不会做出任何先验假设。然而,在许多情况下,场景中包含高层次的几何基元,如直线和平面。这些基元可以提供与兴趣点互补的信息,同时也是三维建模和可视化的重要构建模块。此外,这些基元通常以特定关系排列,即许多直线和平面要么平行,要么正交(周、古川和马2019;周、古川等2020)。这一点在建筑场景和模型中尤为明显,我们将在第13.6.1节中详细讨论。
有时,与其利用场景结构的规律性,不如采用受限运动模型。例如,如果感兴趣的对象是在转盘上旋转(Szeliski1991b),即绕一个固定但未知的轴旋转,可以使用专门的技术来恢复这种运动(Fitzgibbon,Cross,和Zisserman1998)。在其他情况下,摄像机本身可能围绕某个旋转中心沿固定弧线移动(Shum和He1999)。专门的捕捉装置,如移动立体相机架或配备多个固定摄像头的移动车辆,也可以利用单个摄像头相对于捕捉装置(大多)固定的已知信息,如图11.15.34所示。
众所周知,即使相机已经校准,仅凭线对匹配也无法恢复成对的极线几何。要理解这一点,可以想象将每张图像中的线条投影到空间中的三维平面上。你可以随意移动两台相机,仍然能够获得有效的三维线条重建。
当线在三个或更多视图中可见时,可以使用三焦张量将线从一对图像转移到另一对图像(Hartley和Zisserman2004)。也可以仅基于线匹配来计算三焦张量。
施密德和齐瑟曼(1997)描述了一种广泛使用的二维线匹配技术,该技术基于沿共同线段交点的所有像素处的15×15像素相关性得分的平均值。在他们的系统中,假设极线几何已知,例如通过点匹配计算得出。对于宽基线,使用所有可能的通过三维线的平面对应的单应性来扭曲像素,并采用最大相关性得分。对于三张图像的组合,使用三焦张量验证线条是否在几何上对应,然后再评估线段之间的相关性。图11.22展示了他们系统的使用结果。
Bartoli和Sturm(2003)描述了一个完整的系统,用于将从手动线对应关系计算出的三个视图关系(三焦张量)扩展到一个完整的束调整
所有的线和摄像机参数。他们方法的关键是使用Plcker坐标-
参数化线段(2.12),以直接最小化重投影误差。还可以通过端点表示三维线段,并测量每个图像中检测到的二维线段的垂直重投影误差,或使用与线段方向对齐的拉长不确定性椭圆来测量二维误差(Szeliski和Kang 1994)。
贝、法拉利和范古尔(2005)没有重建三维线,而是使用RANSAC将线段聚类为可能共面的子集。随机选取四条线来计算同态矩阵,然后通过评估基于颜色直方图的相关性得分来验证这些及其他合理的线段匹配。属于同一平面的线段的二维交点随后被用作虚拟测量,以估计极线几何,这比直接使用同态矩阵更为准确。
将线条按共面子集分组的另一种方法是根据平行性进行分组。当三条或更多条二维线共享一个共同的消失点时,它们在三维空间中很可能是平行的。通过在图像中找到多个消失点(第7.4.3节),并建立不同图像中这些消失点之间的对应关系,可以直接估计各图像之间的相对旋转(以及通常相机内参)(第11.1.1节)。寻找一组正交的消失点并利用这些消失点来确定全局方向,通常被称为曼哈顿世界假设(Coughlan和Yuille 1999)。Schindler和Dellaert(2004)提出了一种广义版本,其中街道可以在非正交角度相交,称为亚特兰大世界。
舒姆、韩和斯泽利斯基(1998)描述了一种三维建模系统,该系统从多张图像构建校准全景图(第11.4.2节),然后让用户在图像中绘制垂直线和水平线以界定平面区域的边界。这些线条用于确定每个全景图的绝对旋转角度,随后与推断出的顶点和平面一起,用于构建三维结构,可以从一张或多张图像中按比例恢复(图13.20)。
Werner和Zisserman(2002)提出了一种完全自动化的基于线的运动结构方法。在他们的系统中,首先找到线条并根据每张图像中的共同消失点进行分组(第7.4.3节)。然后利用这些消失点来校准相机,即执行“度量升级”(第11.1.1节)。接着使用外观特征(Schmid和Zisserman 1997)和三焦张量匹配与共同消失点对应的线条。这些线条随后用于推断场景中的平面和块状结构模型,具体细节见第13.6.1节。最近的研究还使用深度神经网络从一张或多张图像构建3D线框模型。
基于飞机的技术
在平面结构丰富的场景中,例如建筑领域,可以直接估计不同平面之间的单应性,使用基于特征或基于强度的方法。原则上,这些信息可以同时推断相机姿态和平面方程,即计算基于平面的运动结构。
Luong和Faugeras(1996)展示了如何通过代数运算和最小二乘法直接从两个或多个同态计算出一个基本矩阵。不幸的是,这种方法通常表现不佳,因为代数误差并不对应于有意义的重投影误差(Szeliski和Torr1998)。
更好的方法是在计算每个单应矩阵的区域中虚幻虚拟点对应关系,并将其输入到标准运动算法(Szeliski和Torr 1998)中。更优的方法是使用带有显式平面方程的全束调整,并施加额外约束,以确保重建的共面特征精确位于其对应的平面上。(一种合理的方法是在每个平面上建立一个坐标系,例如在其中一个特征点处,并对其他点使用二维平面内参数化。)Shum、Han和Szeliski(1998)开发的系统展示了这种方法的一个例子,其中场景中各平面的线方向和法向量由用户预先指定。在最近的研究中,Micusik和Wildenauer(2017)在束调整公式中使用平面作为附加约束。其他近期论文则利用线条和/或平面的组合来减少漂移。

图11.23在同时定位和制图(SLAM)中,系统同时估计机器人及其附近地标的位置(Durrant-Whyte和Bailey 2006)©2006 IEEE。
3D重建包括(Zhou,Zou等人,2015),Li,Yao等人(2018),Yang和Scherer
(2019年),和Holynski,Geraghty等人(2020年)。
11.5 同步定位与建图(SLAM)
虽然计算机视觉界自20世纪80年代初(Longuet-Higgins1981)以来一直在研究运动结构,即从多张图像和视频中重建稀疏的3D模型,但移动机器人领域却在平行地研究如何从移动机器人自动构建3D地图。在机器人学中,这一问题被表述为同时估计3D机器人和地标姿态(图11.23),并被称为概率建图(Thrun,Burgard,和Fox2005)和同时定位与建图(SLAM)(Durrant-Whyte和Bailey2006;Bailey和Durrant-Whyte 2006;Cadena,Carlone等人2016)。在计算机视觉界,这一问题最初被称为视觉里程计(Levin和Szeliski2004;Nist r,Naroditsky和Bergen 2006;Maimone,Cheng和Matthies2007),尽管现在通常该术语仅用于不涉及全局地图构建和环闭合的短程运动估计(Cadena,Carlone等人2016)。
早期版本的此类算法使用了超声波、激光等测距技术

图11.24 LSD-SLAM系统的架构(Engel、Sch ps和Cremers
2014)©2014 Springer,显示前端,它执行跟踪、数据关联和局部3D姿态和结构(深度图)更新,以及后端,它执行全局地图优化。
使用测距仪或立体匹配来估计局部三维几何,然后可以将其融合成三维模型。较新的技术可以通过单目相机的视觉特征跟踪来完成相同的任务(Davison,Reid等,2007)。关于这一主题的良好入门教程可以在Durrant-Whyte和Bailey(2006)以及Bailey和Durrant-Whyte(2006)中找到,而更全面的技术综述则见于Fuentes-Pacheco、Ruiz-Ascencio和Rendn-Mancha(2015)以及Cadenas、Carlone等(2016)。
SLAM在两个基本方面与束调整不同。首先,它允许使用多种传感设备,而不仅仅是局限于跟踪或匹配特征点。其次,它在线解决定位问题,即在提供当前传感器姿态时几乎没有延迟。这使得它成为时间关键的机器人应用如自主导航(第11.5.1节)和实时增强现实(第11.5.2节)的首选方法。
SLAM中的一些重要里程碑包括:
单目相机上的SLAM应用(MonoSLAM)(Davison,Reid等人,2007年);
并行跟踪和映射(PTAM)(Klein和Murray2007),将前端(跟踪)和后端(映射)过程(图11.24)拆分为两个以不同速率运行的独立线程(图11.27),然后在照相手机上实现整个过程(Klein和Murray2009);
自适应相对束调整(Sibley、Mei等人,2009年,2010年),它保持了在不同关键帧上锚定的局部重建集合;
增量平滑和映射(iSAM)(Kaess、Ranganathan和Dellaert2008;Kaess、Johannsson等人2012)和其他因子图应用,以处理速度-精度延迟权衡(Dellaert和Kaess2017;Dellaert2021);
•密集跟踪和映射(DTAM)(Newcombe,Lovegrove和Davison2011),它估计并更新每一帧的密集深度映射;
ORB-SLAM(Mur-Artal,Montiel和Tardos2015)和ORB-SLAM2(Mur-Artal和Tard s2017),处理
单目、立体和RGB-D相机以及回环闭合;
SVO(半直接视觉里程计)(Forster,Zhang等人,2017),它结合了基于补丁的跟踪和经典束调整;
LSD-SLAM(大规模直接SLAM)(Engel、Sch ps和Cremers2014
)和DSO(直接稀疏里程计)(Engel、Koltun和Cremers2018),仅在梯度强度位置保留深度估计值(图11.24)。
BAD SLAM(束调整直接RGB-D SLAM)(Sch ps、Sattler和Pollefeys,2019a)。
许多系统都有开源实现。一些广泛使用的基准测试包括:RGB-D SLAM系统的基准测试(Sturm,Engelhard等,2012年),KITTI视觉里程计/ SLAM基准测试(Geiger,Lenz等,2013年),合成ICL-NUIM数据集(Handa,Whelan等,2014年),TUM单目视觉数据集(Engel,Usenko和Cremers,2016年),EuRoC MAV数据集(Burri,Nikolic等,2016年),ETH3D SLAM基准测试(Sch ps,Sattler和Pollefeys,2019a),以及GSLAM通用SLAM基准测试
(Zhao,Xu等,2019年)。
最近的SLAM趋势是与视觉惯性里程计(VIO)算法的集成(Mourikis和Roumeliotis 2007;Li和Mourikis 2013;Forster、Carlone等人2016),这些算法结合了高频惯性测量单元(IMU)测量数据和视觉轨迹,以消除低频漂移。由于IMU现在在手机和运动相机等消费设备中已十分普遍,因此VIO增强的SLAM系统成为了广泛使用的移动增强现实框架如ARKit和ARCore的基础(第11.5.2节)。开源VIO系统的数据集和评估可参见Schubert、Goll等人(2018)。

图11.25自动车辆:(a)斯坦福车(Moravec1983)©1983 IEEE;(b) Junior:斯坦福在城市挑战赛中的参赛作品(Montemerlo,Becker等人2008)©2008 Wiley;(c-d)CVPR 2019展览现场的自动驾驶汽车原型。
正如你从这个简要概述中可以看出,SLAM是一个极其丰富且迅速发展的研究领域,充满了挑战性的稳健优化和实时性能问题。一个很好的资源是KITTI视觉里程计/SLAM评估(Geiger,Lenz和Urtasun 2012)以及重新发布的文献列表,可以找到最近的论文和算法。
关于自动驾驶计算机视觉的调查论文(Janai,G ney等人,2020年,
第13.2节)。
自从人工智能和机器人技术的早期,计算机视觉就被用于
为灵巧机器人提供操作,为自主机器人提供导航(Janai,G ney
等,2020;Kubota2019)。一些最早的基于视觉的导航系统包括斯坦福车(图11.25a)和CMU漫游者(Moravec1980,1983)、Terregator (Wallace,Stentz等人,1985)和CMU Nablab (Thorpe,Hebert等人,1988),这些系统

图11.26全自动Skydio R1无人机在野外飞行©2019 Skydio:(a)多个输入图像和深度图;(b)完全集成的3D地图(Cross2019)。
最初只能每10秒前进4米(< 1英里/小时),这也是第一个使用神经网络进行驾驶的系统(Pomerleau1989)。
早期算法和技术迅速进步,迪克曼斯和米斯利维茨(1992)的VaMoRs系统运行着一个25赫兹的卡尔曼滤波循环,并在100 km/h的车道标记下表现出色。到2000年代中期,当DARPA推出其大挑战赛和城市挑战赛时,配备了测距激光雷达相机和立体相机的车辆能够穿越崎岖的户外地形,并以常规的人类驾驶速度导航城市街道(乌姆森、安哈特等人,2008;蒙特梅罗、贝克等人,2008)。这些系统促使谷歌和特斯拉等公司成立了工业研究项目,以及众多初创企业,其中许多企业在计算机视觉会议上展示他们的车辆(图11.25c-d)。
对自动驾驶汽车的计算机视觉技术进行全面的回顾
可以在Janai、G ney等人(2020)的调查中找到,该调查还附带了一个有用的在线版本
相关论文的可视化工具。40调查包括大量视觉算法和组件的章节,这些算法和组件用于自主导航,涵盖数据集和基准测试、传感器、物体检测与跟踪、分割、立体视觉、流场和场景流场、SLAM、场景理解以及自动驾驶行为的端到端学习。
除了轮式(和腿式)机器人和车辆的自主导航,com-

图11.27 3D增强现实:(a)达斯·维达和一群伊沃克人在一张桌面上展开激战,该桌面是通过实时关键帧结构从运动(Klein和Murray 2007)©2007 IEEE;(b)一个虚拟茶壶固定在现实世界的咖啡杯顶部,其姿态在每个时间帧中重新识别(Gordon和Lowe 2006)©2007斯普林格。
计算机视觉算法广泛应用于自主无人机的控制,既包括娱乐应用(Ackerman 2019)(图11.26),也包括无人机竞速(Jung,Hwang等2018;Kaufmann,Gehrig等2019)。Gareth Cross(2019)在ICRA 2019关于自主飞行中学习系统算法与架构的工作坊以及Pieter Abbeel(2019)高级机器人课程的第23讲中,详细介绍了Skydio的视觉自主导航方法,该课程还有许多其他有趣的相关讲座。
另一个密切相关应用是增强现实,其中3D物体实时插入视频流中,通常用于标注或帮助用户理解场景(Azuma,Bail- lot等2001;Feiner 2002;Billinghurst,Clark和Lee 2015)。传统系统需要事先了解被视觉跟踪的场景或物体(Rosten和Drum-mond 2005),而新系统则可以同时构建3D环境模型并进行跟踪,以便叠加图形(Reitmayr和Drummond 2006;Wagner,Reitmayr等2008)。
Klein和Murray(2007)描述了一个并行跟踪和映射(PTAM)系统,
同时对从视频中选择的关键帧进行完整的捆绑调整
在中间帧上执行稳健的实时姿态估计(Figure11.27a)时,流。
一旦初步重建了3D场景,就会估计出一个主要平面(在这种情况下是桌面),然后虚拟插入3D动画角色。Klein和Murray(2008)扩展了该系统,通过增加边缘特征来处理更快的摄像机运动,即使兴趣点变得过于模糊,这些特征仍然可以被跟踪。他们还使用了一种直接的(基于强度的)旋转估计算法,以实现更快速的运动。
戈登和洛(2006)没有将整个场景建模为一个刚性参考框架,而是首先使用特征匹配和运动结构技术构建单个物体的三维模型。系统初始化后,对于每一帧新图像,他们通过三维实例识别算法找到该物体及其姿态,然后将其图形对象叠加到模型上,如图11.27b所示。
尽管可靠地跟踪此类物体和环境现在是一个已解决的问题,随着ARKit、ARCore和Spark AR等框架被广泛用于移动AR应用开发,确定哪些像素应该被前景场景元素遮挡(Chuang,Agarwala等人,2002;Wang和Cohen,2009)仍然是一个活跃的研究领域。
最近的一个例子是Valentin、Kowdle等人(2018)开发的智能手机AR系统,如图Figure11.28所示。该系统通过将当前帧与前一关键帧匹配,使用CRF后进行滤波步骤,生成半密集深度图。然后利用一种新颖的平面双边求解器将此地图插值至全分辨率,并用于遮挡效果。由于精确的逐像素深度是增强现实效果的关键组成部分,我们很可能会看到这一领域在主动和被动深度传感技术方面的快速进展。
11.6 额外阅读
相机校准最初在摄影测量学中被研究(Brown 1971;Slama 1980;Atkinson 1996;Kraus 1997),但在计算机视觉领域也得到了广泛研究(Tsai 1987;Gremban、Thorpe和Kanade 1988;Champleboux、Lavall e等1992b;Zhang 2000
;Grossberg和Nayar 2001)。通过矩形校准物体或建筑观察到的消失点常用于进行初步校准(Caprile和Torre 1990;Becker和Bove 1995;Liebowitz和Zisserman 1998;Cipolla、Drummond和Robertson 1999;Antone和Teller 2002;Criminisi、Reid和Zisserman 2000;Hartley和Zisserman 2004;Pflugfelder 2008)。不使用已知目标进行相机校准被称为
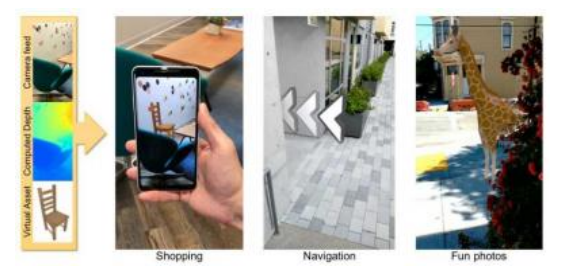
图11.28智能手机增强现实显示实时深度遮挡效果(Valentin,Kowdle等人,2018)©2018 ACM。
自校准在关于运动结构的教科书和调查中都有讨论(Faugeras、Luong和Maybank 1992;Hartley和Zisserman 2004;Moons、Van Gool和Vergauwen 2010)。其中一种流行的技术子集使用纯旋转运动(Stein 1995;Hartley 1997b;Hartley、Hayman等2000;de Agapito、Hayman和Reid 2001;Kang和Weiss 1999;Shum和Szeliski 2000;Frahm和Koch 2003)。
注册3D点数据集的主题被称为绝对定向(Horn1987)和3D姿态估计(Lorusso,Eggert,和Fisher1995)。已经开发了多种技术,同时计算3D点对应及其相应的刚性变换(Besl和McKay1992;Zhang1994;Szeliski和Lavalle1996;Gold,Rangarajan等人1998;David,DeMenthon等人2004;Li和Hartley2007;Enqvist
,Joseph-Son和Kahl2009)。当只有2D观测时,已经开发了多种线性PnP(透视n点)算法(DeMenthon和Davis1995;Quan和Lan1999;Moreno-Noguer,Lepetit,和Fua2007;Terzakis和Lourakis2020)。最近的姿态估计方法使用深度网络(Arandjelovic,Gronat等人2016;Brachmann,Krull等人2017;Xiang,Schmidt等人2018;Oberweger,Rad,和Lepetit2018;Hu,Hugonot等人2019;Peng,Liu等人2019)。从RGB-D图像中估计姿态也非常活跃(Drost,Ulrich等人2010;Brachmann,Michel等人2016;Labb,Carpentier等人2020)。除了用于机器人任务的对象姿态识别外,姿态估计还广泛应用于位置识别(Sattler,Zhou等人2019
;Revaud,Weinzaepfel等人2019;Zhou,Sattler等人2019;Sarlin,DeTone等人2020;Luo,Zhou等人2020)。
关于运动结构的主题在多视图几何的书籍和综述文章中得到了广泛的讨论(Faugeras和Luong2001;Hartley和Zisserman2004;Moons,Van
Gool和Vergauwen2010)对zyes¸il、Voroninski的最新发展进行了调查
等人(2017)。对于两帧重建,哈特利(1997a)撰写了一篇关于“八点算法”的高度引用论文,该算法用于计算具有合理点归一化的本质或基本矩阵。当相机已校准时,可以结合RANSAC使用Nist r(2004)的五点算法,从最少数量的点中获得初始重建。当相机
未校准时,哈特利和齐瑟曼(2004)以及穆恩斯、范古尔和维尔高文(2010)的研究中提供了各种自校准技术。
特里格斯、麦克劳克兰等人(1999)提供了关于束调整的良好教程和综述,而劳拉基斯和阿尔吉罗斯(2009)以及恩格尔、斯图尼乌斯和尼斯特
(2006)则提供了实施和有效实践的建议。束调整也在多视图几何的教科书和综述中有所涉及(福加拉斯和隆2001;哈特利和齐瑟曼2004;穆恩斯、范古尔和维尔高文2010)。处理更大问题的技术由斯纳维利、塞茨和舍利斯基(2008b)、阿加瓦尔、塞茨等人(2009)、阿加瓦尔、塞茨等人(2010)、郑、尼斯特等人(2012)、吴(2013)、海因利、施纳伯格等
人(2015)、施纳伯格和弗拉姆(2016
)以及德拉特和凯斯(2017
)描述。虽然束调整通常被称为增量重建算法中的内循环(斯纳维利、塞茨和舍利斯基2006),但也有层次化(菲茨吉本和齐瑟曼1998;法伦泽纳、富西埃洛和格拉迪2009)和全局(罗瑟和卡尔松2002;马蒂内克和帕伊德拉2007;辛哈、斯特迪和舍利斯基2010;姜、崔和谭2013;莫隆、莫纳塞和马莱特2013;
Wilson和Snavely2014;Cui和Tan2015;zyes¸il和Singer2015;Holynski和Geraghty
(et al.2020)提出的初始化方法也是可能的,甚至可能是可取的。
在机器人领域,从移动机器人重建三维环境的技术被称为同时定位与建图(SLAM)(Thrun、Burgard和Fox 2005;Durrant-Whyte和Bailey 2006;Bailey和Durrant-Whyte 2006;Fuentes-Pacheco、Ruiz-Ascencio和Rendn-Mancha 2015;Cadena、Carlone等2016)。SLAM与束调整不同之处在于它允许使用
多种传感设备,并且能够在线解决定位问题。这使得它成为时间敏感型机器人的首选方法。
诸如自主导航(Janai,G ney等人,2020)和实时增强等应用
增强现实(Valentin,Kowdle等人,2018)。该领域的重点论文包括(Davison,Reid等人,2007;Klein和Murray,2007,2009;Newcombe,Lovegrove和Davison,2011;Kaess,Johannsson等人,2012;Engel
,Sch ps和Cremers,2014
;Mur-Artal和Tard s,2017;Forster,Zhang等人,2017;Dellaert和Kaess,2017;Engel,Koltun
和Cremers,2018;Sch ps,Sattler和Pollefeys,2019a)以及将SLAM与IMU结合以获得视觉惯性里程计(VIO)的论文(Mourikis和Roumeliotis,2007;Li和Mourikis,2013;Forster,Carlone等人,2016;Schubert,Goll等人,2018)。
Chapter 12 Depth estimation
12.1极点几何 753
12.1.1整改 755
12.1.2平面扫描 757
12.2稀疏对应 760
12.2.1三维曲线和剖面 760
12.3密集通信 762
12.3.1相似性度量 764
12.4地方方法 766
12.4.1亚像素估计和不确定性 768
12.4.2应用:基于立体声的头部跟踪 769
12.5全球优化 771
12.5.1动态规划 774
12.5.2基于分割的技术 775
12.5.3应用:Z键和背景替换 777
12.6深度神经网络 778
12.7多视图立体 781
12.7.1场景流 785
12.7.2体积和三维表面重建 786
12.7.3从轮廓中提取形状 794
12.8单眼深度估计 796
12.9额外阅读材料 799
12.10Exercises 800

图12.1深度估计算法可以将一对彩色图像(a-b)转换为深度图(c) (Scharstein,Hirschm ller等,2014)©2014斯普林格,将一系列图像(d)转换为3D模型(e) (Knapitsch,Park等,2017)©2017 ACM,或将单个图像(f)转换为深度图(g) (Li,Dekel等,2019)©2019 IEEE。
立体匹配是通过找到图像中的匹配像素并将它们的二维位置转换为三维深度,从而构建场景的三维模型的过程。在第十一章中,我们介绍了恢复相机位置和构建场景或物体稀疏三维模型的技术。本章我们将探讨如何构建更完整的三维模型,例如,为输入图像中的像素分配相对深度的稀疏或密集深度图。我们还将讨论多视图立体算法,这些算法可以生成完整的三维体积或基于表面的对象模型,以及单目深度恢复算法,这些算法仅从一张图像推断出合理的深度。
为什么人们对深度估计和立体匹配感兴趣?从最早的视觉感知研究开始,我们就知道我们是根据左右眼外观差异来感知深度的。1作为一个简单的实验,将你的手指垂直放在眼前,交替闭上每只眼睛。你会注意到手指相对于场景背景在左右移动。同样的现象也出现在图12.1a-b所示的图像对中,其中前景物体相对于背景向左或向右移动。
正如我们即将看到的,在简单的成像配置下(无论是双眼还是直视前方的相机),水平运动或视差的量与观察者距离成反比。虽然视觉视差与场景结构之间的基本物理和几何关系已经非常清楚(第12.1节),但通过建立密集且准确的图像间对应关系来自动测量这种视差是一项具有挑战性的任务。
最早的立体匹配算法是在摄影测量领域开发的,用于从重叠的航拍图像中自动构建地形高程图。在此之前,操作员会使用摄影测量立体绘图仪,该设备向每只眼睛显示这些图像的偏移版本,并允许操作员在恒定高程轮廓上浮动一个点光标。全自动立体匹配算法的发展是这一领域的重大进步,使得航拍图像的处理速度更快、成本更低(Hannah 1974;Hsieh,McKeown和Perlant 1992)。
在计算机视觉领域,立体匹配一直是研究最为广泛且基础性的问题之一(Marr和Poggio 1976;Barnard和Fischler 1982;Dhond和Aggarwal 1989;Scharstein和Szeliski 2002;Brown、Burschka和Hager 2003;Seitz、Curless等2006),并且仍然是最活跃的研究领域之一(Poggi、Tosi等2021)。虽然摄影测量匹配主要集中在航空影像上,但计算机视觉应用还包括建模人类视觉系统(Marr 1982)、机器人导航和操作(Moravec 1983;Konolige 1997;Thrun、Montemerlo等2006;Janai,
1立体这个词来自希腊语,意思是“固体”;立体视觉就是我们感知固体形状的方式(Koenderink 1990)。

图12.2立体视觉的应用:(a)输入图像,(b)计算深度图,(c)多视图立体生成新视图(Matthies、Kanade和Szeliski 1989)©1989斯普林格;(d)两幅图像之间的视图变形(Seitz和Dyer 1996)©1996 ACM;(e–f)
3Dface建模(图片由Frdric Devernay提供);(g)z键实时和计算机
生成的图像(Kanade,Yoshida等人,1996)©1996 IEEE;(h-i)从虚拟现实中的多个视频流中构建建筑物三维表面模型(Kanade,Rander和Narayanan,1997)©1997 IEEE;(j)计算深度图以实现自主导航(Geiger,Lenz和Urtasun,2012)©2012 IEEE。
G ney等人(2020)和Figures12.2j和11.26,以及视图插值和基于图像的渲染(图12.2a-d),3D模型构建(图12.2e-f和h-i),将实拍与计算机生成的图像混合(图12.2g),以及增强现实(Valentin,Kowdle等人2018;Chaurasia,Nieuwoudt等人2020)和Figure11.28。
在本章中,我们描述了立体匹配背后的基本原理,遵循Scharstein和Szeliski(2002)提出的通用分类法。我们在第12.1节回顾了立体图像匹配的几何问题,即如何计算给定像素在一个图像中的可能位置范围,即其极线。我们介绍了如何预变形图像,使对应的极线重合(校正)。我们还介绍了一种称为平面扫描的一般重采样算法,该算法可用于具有任意相机配置的多图像立体匹配。
接下来,我们简要回顾用于稀疏立体匹配兴趣点和边缘特征的技术(第12.2节)。然后,我们将转向本章的主要主题,即以视差图形式估计大量像素级对应关系(图12.1c)。这首先涉及选择一个像素匹配标准(第12.3节),然后使用局部区域聚合(第12.4节)、全局优化(第12.5节)或深度网络(第12.6节),来帮助消除潜在匹配的不确定性。在第12.7节中,我们讨论了多视角立体技术,该技术利用超过两对图像来生成更高质量的深度图或完整的3D物体或场景模型(图12.1d-e)。最后,在第12.8节中,我们介绍了仅从单张图像推断深度的算法,这些算法现在已通过机器学习和深度网络成为可能。
在本章中,我们将经常提到用于开发深度推断算法并评估其性能的数据集和基准测试。其中最广泛使用且最具影响力的包括米德尔伯里立体和多视图数据集基准测试,这些是最早更新排行榜的数据集之一;EPFL多视图数据集;KITTI自动驾驶基准测试(包括立体、流场、场景流场等);DTU数据集;ETH3D基准测试;坦克与寺庙基准测试;以及BlendedMVS数据集,所有这些都在表12.1中进行了总结。更多数据集的指向可以参见
在Mayer,Ilg等人(2018)、Janai,G ney等人(2020)、Laga,Jospin等人(2020)和Poggi等人中,
Tosi等人(2021)。
12.1 极点几何
给定一个图像中的像素,我们如何计算它在另一个图像中的对应关系?在第9章中,我们看到可以使用各种搜索技术来匹配基于
| 名称/网址 | 内容/参考 |
| 米德尔伯里立体声 https://vision.middlebury.edu/stereo 米德尔伯里多视图 https://vision.middlebury.edu/mview 伊诺克·普拉特自由图书馆 (不再活跃)KITTI 2015 http://www.cvlibs.net/datasets/kitti/eval-stereo-flow.php 丹麦技术大学 https://roboimagedata.compute.dtu.dk/?page-id=36 弗赖堡场景流 https://lmb.informatik.uni-freiburg.de/resources/datasets 三维 https://www.eth3d.net 坦克和寺庙 https://www.tanksandtemples.org 混合MVS https://github.com/YoYo000/BlendedMVS | 33高分辨率立体对 (Scharstein,Hirschm ller等人,2014) 从300+视图中扫描的6个3D对象(Seitz、Curless等人,2006) 6套室外多视角图像(Strecha,von Hansen等人,2008) 200个训练+ 200个测试立体声对(Menze和Geiger,2015) 124个场景,每个场景包含49-64张图像(Jensen,Dahl等人,2014) 39k合成立体声对(Mayer,Ilg等人,2018) 13次训练+ 12次测试高分辨率场景(Sch ps,Sch nberger等人,2017 ) 7次训练+ 14次测试4K视频场景(Knapitsch,Park等人,2017) 17k MVS图像,覆盖113个场景(Yao,Luo等人,2020) |
它们的局部外观以及邻近像素的运动。然而,在立体匹配的情况下,我们有一些额外的信息可用,即拍摄同一静态场景的照片的相机的位置和校准数据(第11.3节)。
我们如何利用这些信息来减少潜在对应点的数量,从而加快匹配速度并提高其可靠性?图12.3a展示了图像x0中的一个像素如何投影到另一张图像中的极线段。该线段一端由原始视线在无穷远处的投影p∞限定,另一端则由原始相机中心c0在第二台相机中的投影限定,这被称为极线e1。如果我们把第二张图像中的极线重新投影回第一张图像,就会得到另一条线(线段),这次由另一个对应的极点e0限定。将这两条线段延伸至无穷远,我们得到一对对应的极线(图12.3b),它们是两个图像平面与通过两台相机中心c0和c1以及兴趣点p的极平面相交的结果(Faugeras和Luong 2001;Hartley和Zisserman 2004)。

图12.3极线几何:(a)对应于一条射线的极线段;(b)对应的极线集合及其极平面。
正如我们在第11.3节中所见,一对相机的极线几何关系隐含于相机的相对姿态和校准中,可以使用基础矩阵(或校准后的本质矩阵,即五点或更多点)轻松计算出七个或更多点的匹配(Zhang1998a,b;Faugeras和Luong2001;Hartley和Zisserman2004)。一旦计算出这种几何关系,我们就可以利用一个图像中像素对应的极线来限制另一个图像中相应像素的搜索范围。一种方法是使用一般的对应算法,如光流(第9.3节),但仅考虑沿极线的位置(或将任何衰减的流向量投影回该线上)。
通过首先校正(即变形)输入图像,使相应的水平扫描线成为极线,可以得到更高效的算法(Loop和Zhang 1999;Faugeras和Luong 2001;Hartley和Zisserman 2004)。之后,可以在计算匹配分数的同时独立地匹配水平扫描线或水平移动图像(图12.4)。
校正两个图像的一种简单方法是首先旋转两个摄像机,使它们的视线垂直于连接摄像机中心c0和c1的直线。由于倾斜方向存在一定的自由度,因此应使用能够实现这一目标的最小旋转角度。接下来,
这在摄像机相邻时最为合理,尽管通过旋转摄像机,可以对任何未过度倾斜或尺度变化不大的摄像机对进行校正。在后一种情况下,使用平面扫描(见下文)或假设三维空间中的小平面区域位置(Goesele,Snavely等,2007)可能更为合适。

图12.4 Loop和Zhang(1999)提出的多级立体校正算法©
1999 IEEE。(a)原始图像对叠加了几条极线;(b)图像变换使极线平行;(c)图像校正使极线水平且垂直对应;(d)最终校正以最小化水平失真。
确定光轴上的期望扭曲,使向上向量(相机y轴)垂直于相机中心线。这确保了相应的极线是水平的,并且无穷远处点的视差为0。最后,如有必要,重新缩放图像以适应不同的焦距,放大较小的图像以避免混叠。(此过程的详细信息可参见Fusiello、Trucco和Verri(2000)及练习12.1。)当有关成像过程的更多信息可用时,例如图像是在共面的摄影板上形成的,可以开发更专业和准确的算法(Luo、Kong等人,2020)。需要注意的是,通常情况下,除非所有图像的光学中心共线,否则无法同时校正任意一组图像,尽管旋转相机使其指向同一方向可以将相机间的像素移动减少到平移和缩放。
由此产生的标准校正几何被用于许多立体相机设置和立体算法中,并导致3D深度Z和视差d之间非常简单的反向关系,
(12.1)
其中,f是焦距(以像素为单位),B是基线,和
x, = x + d(x, y), y, = y (12.2)

图12.5典型视差空间图像(DSI)的切片(Scharstein和Szeliski
2002)©2002斯普林格:(a)原始彩色图像;(b)地面真实视差;(c–e)=10、16、21的三个(x,y)切片;(f)y=151的一个(x,d)切片((b)中的虚线)。在(c–e)中可以看到各种深色(匹配)区域,例如书架、桌子和罐子,以及头部雕像,在(f)中可以看到三个视差水平作为水平线。DSIs中的深色条带表示在此视差下匹配的区域。(较小的深色区域通常是无纹理区域的结果。)鲍比克和因蒂勒(1999)讨论了更多关于DSI的例子。
描述了左右图像中对应像素坐标之间的关系(Bolles、Baker和Marimont,1987;Okutomi和Kanade,1993;Scharstein和Szeliski,2002)。从一组图像中提取深度的任务就变成了估计视差图d(x,y)。
校正后,我们可以轻松比较对应位置(x,y)和(x,y,)=(x+d,y)的像素相似度,并将它们存储在视差空间图像(DSI)C(x,y,d)中以供进一步处理(图12.5)。视差空间(x,y,d)的概念可以追溯到早期的立体匹配研究(Marr和Poggio 1976),而视差空间图像(体)的概念通常与Yang、Yuille和Lu(1993)以及Intille和Bobick(1994)相关联。
在匹配之前对图像进行预校正的替代方法是,在场景中扫过一组平面,并测量不同图像在重新投影到这些平面上时的光度一致性(图12.6)。这个过程通常被称为平面扫描算法(Collins1996;Szeliski和Golland1999;Saito和Kanade1999)。

图12.6在场景中扫过一组平面(Szeliski和Golland 1999)©1999斯普林格出版社:(a)从虚拟摄像机看到的平面集合会在其他任何源(输入)相机图像中诱导出一组单应性。(b)来自所有其他相机的扭曲~图像可以堆叠成一个广义视差空间体I(x,y,d,k),该空间体由像素位置(x,y)、视差d和相机k编索引。
正如我们在第2.1.4节中介绍的那样,其中我们引入了投影深度(也称为平面加视差(Kumar、Anandan和Hanna1994;Sawhney~ 1994;Szeliski和Coughlan 1997)),一个满秩的4×4投影矩阵P的最后一行可以设置为任意平面
方程p3 = s3 [0 jc0]。由此得到的四维射影变换(共线变换)
(2.68)将三维世界点p = (X,Y,Z,1)映射到屏幕坐标xs =(xs,ys,1,d),其中投影深度(或视差)d(2.66)在参考平面上为0(图2.11)。
如图12.6a所示,通过一系列视差假设对d进行扫描,对应于将每个输入图像映射到定义视差空间的虚拟相机P上,通过一系列单应性(2.68–2.71),
k
~ k -1xs = k
如图2.12k所示,源图像和虚拟
(参考
)图像(Szeliski和Golland 1999)。齐次变换族Hk (d) = Hk + tk [0 0 d]通过添加一个秩为1的矩阵参数化,彼此之间通过平面同构关系相连(Hartley和Zisserman 2004,A5.2)。
虚拟摄像机的选择和参数化取决于应用,这也是该框架具有很大灵活性的原因。在许多应用中,其中一个输入摄像机(
研究的现象,但如果眼睛向内倾斜,垂直差异是可能的。
参考相机)被使用,从而计算出与输入图像之一注册的深度图,该深度图可以用于基于图像的渲染(第14.1节和第14.2节)。在其他应用中,例如视频会议中的视线校正视图插值(第12.4.2节)(Ott、Lewis和Cox 1993;Criminisi、Shotton等2003),最好使用位于两个输入相机之间的中央相机,因为它提供了所需的每像素视差,以虚拟生成中间图像。
选择视差采样,即零视差平面的设置和整数视差的缩放,也取决于具体应用,通常设定为涵盖感兴趣的范围,即工作体积,同时将视差缩放到像素(或亚像素)位移以采样图像。例如,在机器人导航中使用立体视觉进行障碍物避让时,最方便的是设置视差来测量每个像素相对于地面的高度(Ivanchenko,Shen,和Coughlan 2009)。
随着每个输入图像被扭曲到由视差d参数化的当前平面~s上,它可以堆叠成一个广义视差空间图像I(x,y,d,k),以便进一步处理(图12.6b) (Szeliski和Golland 1999)。在大多数立体算法中,相对于参考图像Ir的光一致性(例如平方和或鲁棒差异)会被计算并存储在DSI中。
x, y)). (12.4)
然而,也可以计算其他统计量,如稳健方差、焦点或熵(第12.3.1节)(Vaish,Szeliski等,2006年),或者利用这种表示来推理遮挡问题(Szeliski和Golland,1999年;Kang和Szeliski,2004年)。广义DSI在我们回到第12.7.2节多视图立体话题时将特别有用。
当然,飞机并不是唯一可以用来定义感兴趣空间三维扫描的表面。圆柱面,特别是与全景摄影结合使用时(第8.2节),经常被采用(石黑、山本和辻1992;康和斯泽利斯基1997;舒姆和斯泽利斯基1999;李、舒姆等人2004;郑、康等人2007)。还可以定义其他流形拓扑结构,例如相机绕固定轴旋转的情况(塞茨2001)。
一旦计算出DSI,大多数立体对应算法的下一步是在视差空间d(x,y)中生成一个最佳描述场景表面形状的单值函数。这可以视为在视差空间图像中找到具有某些最优性质的表面,例如最低成本和最佳(分段)平滑度(Yang,Yuille,和Lu 1993)。图12.5展示了典型DSI的切片示例。更多此类图可以在Bobick和Intille(1999)的论文中找到。
12.2 稀疏对应
早期的立体匹配算法基于特征,即首先使用兴趣点算子或边缘检测器提取一组潜在可匹配的图像位置,然后利用基于块的度量方法在其他图像中搜索对应位置(Hannah 1974;Marr和Poggio 1979;Mayhew和Frisby 1980;Baker和Binford 1981;Arnold 1983;Grimson 1985;Ohta和Kanade 1985;Bolles、Baker和Marimont 1987;Matthies、Kanade和Szeliski 1989;Hsieh、McKeown和Perlant 1992;Bolles、Baker和Hannah 1993)。这种对稀疏对应关系的限制部分是由于计算资源的限制,但也出于希望将立体算法产生的结果限制为高置信度匹配的愿望。在某些应用中,还希望匹配具有非常不同光照条件的场景,在这些情况下,边缘可能是唯一稳定的特征(Collins 1996)。这样的稀疏三维重建可以使用表面拟合算法进行插值,如第4.2节和第13.3.1节中讨论的那些。
最近在这个领域的工作主要集中在首先提取高度可靠的特征,然后使用这些特征作为种子来生成更多的匹配(Zhang和Shan2000;Lhuillier和
Quan2002;ech和ra2007
)或作为密集的每个像素深度求解器的输入(Valentin,
Kowdle等人(2018))。类似的方法也被扩展到宽基线多视图立体问题,并与3D表面重建(Lhuillier和Quan,2005;Strecha、Tuytelaars和Van Gool,2003;Goesele、Snavely等人,2007)或自由空间推理(Taylor,2003)相结合,详见第12.7节。
稀疏对应关系的另一个例子是轮廓曲线(或遮挡轮廓)的匹配,这些曲线出现在物体边界处(图12.7),以及内部自遮挡处,表面从摄像机视点偏离。
匹配轮廓曲线的难点在于,通常情况下,轮廓曲线的位置会随着相机视角的变化而变化。因此,直接在两张图像中匹配曲线,然后对这些匹配进行三角测量,可能会导致形状测量出错。幸运的是,如果有三个或更多间隔较近的帧,可以将局部圆弧拟合到相应边缘点的位置(图12.7a),从而直接从匹配中获得半密集的曲面网格(图12.7c和g)。此外,匹配这些曲线的一个优势是,只要前景和背景颜色之间有明显的差异,就可以用于重建未纹理表面的形状。
多年来,已经开发出多种不同的技术,用于从轮廓曲线重建表面形状(Giblin和Weiss1987;Cipolla和Blake1992;Vaillant

图12.7从遮挡轮廓重建表面(Szeliski和Weiss,1998)
©2002斯普林格:极线平面中的圆弧拟合;(b)假设一个截断侧面的椭球体及其椭圆形表面标记的合成示例;(c)从斜视和俯视角度看到的部分重建表面网格;(d)玻璃烟雾机转盘的真实图像序列;(e)提取的边缘;(f)部分重建的轮廓曲线;(g)部分重建的表面网格。(部分重建图为了不使图像过于拥挤而显示。)
以及Faugeras1992;Zheng1994;Boyer和Berger1997;Szeliski和Weiss1998)。Cipolla和Giblin(2000)描述了许多这些技术,以及相关的主题,如从轮廓曲线序列中推断相机运动。下面,我们总结了Szeliski和Weiss(1998)提出的方法,该方法假设一组离散的图像,而不是在连续微分框架中解决问题。
假设相机移动足够平滑,使得局部极线几何变化缓慢,即由连续的相机中心和待考虑的边缘所诱导的极线面几乎共面。处理流程的第一步是从每张输入图像中提取并连接边缘(图12.7b)。接下来,使用成对的极线几何、邻近性和(可选地)外观来匹配连续图像中的边缘。这在时空体积中提供了一组链接的边缘,有时称为编织墙(Baker1989)。
重建单个边缘的三维位置及其局部平面法线
对于曲率,我们将对应于其邻近点的视图光线投影到由相机中心、视图光线和相机速度定义的瞬时极线平面上,如图12.7a所示。然后,我们拟合一个切圆到这些投影线上,从而可以计算出三维点的位置(Szeliski和Weiss 1998)。
生成的3D点集及其空间(图像内)和时间(图像间)邻近点,构成了具有局部法线和曲率估计值的3D表面网格(图12.7c和g)。请注意,每当曲线是由表面标记或锐利折痕边缘引起时,而不是平滑的表面轮廓曲线,这会表现为0或小的曲率半径。这样的曲线会导致孤立的3D空间曲线,而不是平滑表面网格的元素,但在后续的表面插值阶段(第13.3.1节),仍可将其纳入3D表面模型中。
最近关于从RGB和RGB- D图像序列中重建三维曲线的例子包括(李、姚等,2018;刘、陈等,2018;王、刘等,2020),其中最新的一项研究甚至能够在没有纹理背景的情况下恢复相机姿态。当被建模的细小结构是平面流形,如叶子或纸张,而不是真正的三维曲线,例如电线时,特别定制的网格表示可能更为合适。
(Kim,Zimmer等人,2013;Y cer,Kim等人,2016;Y cer,Sorkine-Hornung等人,2016),如图所示
在第12.7.2节和第14.3节中进行了更详细的讨论。
12.3 密集通信
虽然稀疏匹配算法偶尔仍被使用,但如今大多数立体匹配算法都集中在密集对应上,因为这适用于基于图像的渲染或建模等应用。这个问题比稀疏对应更具挑战性,因为在无纹理区域推断深度值需要一定的猜测。(想象一下透过栅栏看到的纯色背景,它的深度应该是多少?)
在本节中,我们回顾了由Scharstein和Szeliski(2002)首次提出的密集对应算法的分类体系。该分类体系包含一组算法“构建模块”,可以从中构建出大量算法。它基于这样的观察:立体算法通常执行以下四个步骤中的某些子集:
1.匹配成本计算;
2.成本(支持)聚合;
3.差异计算与优化;
4.差异细化。
例如,局部(基于窗口的)算法(第12.4节),其中给定点的视差计算仅依赖于有限窗口内的强度值,通常通过聚合支持来隐式假设平滑性。这些算法中的一些可以清晰地分解为步骤1、2、3。例如,传统的平方差之和(SSD)算法可以描述为:
1.匹配成本是给定视差下强度值的平方差。
2.聚合是通过在具有恒定视差的正方形窗口上求匹配成本之和来完成的。
3.通过选择每个像素的最小(获胜)聚合值来计算差异。
然而,一些局部算法结合了步骤1和2,并使用基于支持区域的匹配成本,例如归一化互相关(Hannah 1974;Bolles、Baker和Hannah 1993)以及秩变换(Zabih和Woodfill 1994)和其他序数度量(Bhat和Nayar 1998)。(这也可以视为预处理步骤;见第12.3.1节。)
另一方面,全局算法明确地假设平滑性,然后解决一个全局优化问题(第12.5节)。这类算法通常不执行聚合步骤,而是寻找一种视差分配(步骤3),以最小化由数据(步骤1)项和平滑性项组成的全局成本函数。这些算法之间的主要区别在于所使用的最小化过程,例如模拟退火(Marroquin、Mitter和Poggio 1987;Barnard 1989)、概率(平均场)扩散(Scharstein和Szeliski 1998)、期望最大化(EM)(Birchfield、Natarajan和Tomasi 2007)、图割(Boykov、Veksler和Zabih 2001)或循环信念传播(Sun、Zheng和Shum 2003),仅举几例。
在这两大类之间,存在一些迭代算法,它们不明确指定要最小化的全局函数,但其行为与迭代优化算法非常相似(Marr和Poggio 1976;Zitnick和Kanade 2000)。层次(粗到细)算法类似于这些迭代算法,但通常在图像金字塔上操作,其中较粗层次的结果用于限制更精细层次的局部搜索(Witkin、Terzopoulos和Kass 1987;Quam 1984;Bergen、Anandan等1992)。此外,在局部和全局方法之间还存在半全局匹配(SGM)(Hirschm ller 2008),该方法通过一维优化近似最小化二维成本函数(见第12.5.1节),以及避免探索整个搜索空间的方法,例如PatchMatch双目(Bleyer、Remann和Rother 2011)和局部平面扫描(LPS)。
(Sinha、Scharstein和Szeliski2014)。还开发了大量用于立体匹配的神经网络算法,我们将在第12.6节中回顾这些算法。
虽然大多数立体匹配算法针对参考输入图像生成单一视差图,或编码连续表面的视差空间路径(图12.13),但少数算法还计算每个像素的分数不透明度值以及深度和颜色(Szeliski和Golland 1999;Zhou、Tucker等2018;Flynn、Broxton等2019)。由于这些方法与体重建技术密切相关,我们将在第12.7.2节以及第14.2.1节关于基于图像的渲染层中讨论。
任何密集立体匹配算法的第一个组成部分是相似性度量,它通过比较像素值来确定它们对应的可能性。在本节中,我们将简要回顾第9.1节介绍的相似性度量,并提及一些专门为立体匹配开发的其他度量(Scharstein和Szeliski
2002年;Hirschm ller和Scharstein2009)。
最常见的基于像素的匹配成本包括平方强度差(SSD)(Hannah 1974)和绝对强度差(SAD)(Kanade 1994)。在视频处理领域,这些匹配标准被称为均方误差(MSE)和均绝对差(MAD);术语“位移帧差”也经常被使用(Tekalp1995)。
最近,提出了几种稳健的度量方法(9.2),包括截断二次函数和污染高斯分布(Black和Anandan 1996;Black和Rangarajan 1996;Scharstein和Szeliski 1998;Barron 2019)。这些度量方法之所以有用,是因为它们限制了聚合过程中不匹配的影响。Vaish、Szeliski等人(2006)比较了多种此类稳健度量方法,其中包括一种基于每个视差假设下像素值熵的新方法(Zitnick、Kang等人2004),该方法在多视图立体中特别有用。
其他传统的匹配成本包括归一化互相关(9.11)(Hannah 1974;Bolles、Baker和Hannah 1993;Evan Evangelidis和Psarakis 2008),其行为类似于平方差之和(SSD),以及基于二进制特征的二值匹配成本(即匹配或不匹配)(Marr和Poggio 1976),这些特征如边缘(Baker和Binford 1981;Grimson 1985)或拉普拉斯算子的符号(Nishihara 1984)。由于它们的区分能力较差,简单的二值匹配成本已不再用于密集立体匹配。 某些成本对相机增益或偏置的差异不敏感,例如基于梯度的测量(Seitz1989;Scharstein1994)、相位和滤波器组响应(Marr和Poggio1979;Kass1988;Jenkin、Jepson和Tsotsos1991;Jones和Malik1992)、滤波器

图12.8 Hirschm ller和Scharstein(2009)研究的各种相似性度量(预处理滤波器)©2009 IEEE。为了更好地可视化,(b)-(d)的对比度已提高。
这些方法包括移除常规或稳健(双边滤波)均值(Ansar,Castano和Matthies 2004;Hirschm ller和Scharstein 2009),密集特征描述符(Tola,Lepetit和Fua 2010),以及非参数度量如秩和普查变换(Zabih和Woodfill 1994),序数度量(Bhat和Nayar 1998),或熵(Zitnick,Kang等2004;Zitnick和Kang 2007)。普查变换将移动窗口内的每个像素转换为一个位向量,表示哪些邻居像素高于或低于中心像素,Hirschm ller和Scharstein(2009)发现这种变换对大规模、非平稳的光照变化具有很强的鲁棒性。图12.8展示了几种可以应用于图像以提高其在光照变化下的相似性的变换。
还可以通过执行预处理或迭代细化步骤来校正不同的全局摄像机特性,该步骤使用全局回归(Gennert1988)、直方图均衡(Cox、Roy和Hingorani 1995)或互信息(Kim、Kolmogorov和Zabih2003;Hirschm ller2008)估计图像间偏差增益变化。还提出了局部平滑变化补偿场(Strecha、Tuytelaars和Van Gool2003;Zhang、McMillan和Yu2006)。
为了补偿采样问题,即高频区域像素值的巨大差异,伯奇菲尔德和托马西(1998)提出了一种匹配成本,这种成本对图像采样的位移不那么敏感。他们不是仅仅比较整数倍移动的像素值(这可能会错过有效的匹配),而是将参考图像中的每个像素与另一图像的线性插值函数进行比较。关于这些及其他匹配成本的更详细研究见于斯泽利斯基和沙尔斯坦(2004)以及希施米勒和沙尔斯坦(2009)。特别是,如果你预期要匹配的图像之间存在显著的曝光或外观变化,那么在希施米勒和沙尔斯坦(2009)评估中表现良好的一些更稳健的度量方法,如普查变换(扎比和伍德菲尔德1994)、序数度量(巴特和纳亚尔1998)、双边减法(安萨尔、卡斯塔诺和马蒂斯2004)或层次互信息(希施米勒2008),应该被使用。有趣的是,当利用颜色信息时,似乎并没有帮助。
成本(Bleyer和Chambon 2010),尽管它对于聚合很重要(将在下一节讨论)。当匹配多于两对图像时,可以使用更复杂的相似性(照片一致性)度量变体,如第12.7节和(Furukawa和Hern ndez 2015,第2章)所述。
最近,深度学习在立体声方面的第一个成功之一就是学习
匹配成本。bontar和LeCun(2016)训练了一个神经网络来比较图像
在从中部伯里(Scharstein,Hirschm ller等人,2014)提取的数据上训练的补丁
以及KITTI(Geiger、Lenz和Urtasun2012)数据集。这种匹配成本仍然被广泛用于这两个基准上的顶级方法中。
12.4 地方方法
局部和基于窗口的方法通过在DSI C(x,y,d)中的支撑区域求和或平均来聚合匹配成本。支撑区域可以是固定视差下的二维区域(有利于前平行表面),也可以是在x-y-d空间中的三维区域(支持倾斜表面)。二维证据聚合已使用方形窗口或高斯卷积(传统方法)、多个锚定在不同点的窗口,即可移动窗口(Arnold1983;Fusiello,Roberto和Trucco1997;Bobick和Intille1999)、具有自适应大小的窗口(Okutomi和Kanade1992;Kanade和Okutomi1994;Kang,Szeliski和Chai2001;Veksler2001,2003)、基于恒定视差连通组件的窗口(Boykov,Veksler和Zabih1998)、基于颜色分割的结果(Yoon和Kweon2006;Tombari,Mattoccia等2008),或带有引导滤波器的方法(Hosni,Rhemann等2013)实现。提出的三维支撑函数包括有限视差差异(Grimson1985)、有限视差梯度(Pollard,Mayhew,和Frisby1985)、Prazdny的相干性原理(Prazdny1985),以及Zitnick和Kanade(2000)的工作,其中包括可见性和遮挡推理。PatchMatch双目立体(Bleyer,Rhemann,和Rother2011)也在下文详细讨论,通过倾斜的支撑窗口在三维中进行聚合。
使用二维或三维卷积,C(x,y,d)= w(x,y,d)* C0(x,y,d),可以执行具有固定支持区域的聚合。 (12.5)
或者,在矩形窗口的情况下,使用高效的移动平均框滤波器(第3.2.2节)(Kanade,Yoshida等人,1996;Kimura,Shinbo等人,1999)。可移动窗口也可以通过使用可分离的滑动最小滤波器(图12.9) (Scharstein
4关于此类技术的两项调查和比较,请参见Gong、Yang等人(2007)和Tombari、Mattoccia等人(2008)的工作。

图12.9可移动窗口(Scharstein和Szeliski 2002)©2002斯普林格。尝试在黑色像素周围所有3×3移动窗口的效果,与在同一邻域内取所有居中(未移动)窗口的最小匹配得分相同。(为了清晰起见,这里仅显示了三个相邻的移动窗口。)

图12.10根据图像内容调整的聚合窗口大小和权重(Tombari,Mattoccia等人,2008)©2008 IEEE:(a)原始图像和选定的评估点;
(b)可变窗口(Veksler 2003);(c)自适应权重(Yoon和Kweon 2006);(d)基于分割(Tombari、Mattoccia和Di Stefano 2007)。注意,自适应权重和基于分割的技术会根据颜色相似的像素调整其支持范围。
以及Szeliski2002,第4.2节)。通过首先计算总和面积表(第3.2.3,3.30-3.32节)(Veksler2003),可以选择不同形状和大小的窗口,从而更高效地进行选择。选择合适的窗口非常重要,因为窗口必须足够大以包含足够的纹理,同时又不能太大以至于跨越深度不连续处(图12.10)。另一种聚合方法是迭代扩散,即反复将每个像素的成本与其邻近像素成本的加权值相加(Szeliski和Hinton 1985;Shah 1993;Scharstein和Szeliski 1998)。
贡、杨等人(2007)和汤巴里、马托奇亚等人(2008)比较的局部聚合方法中,维克勒(2003)的快速可变窗口方法和尹和奎恩(2006)开发的局部加权方法始终表现出在性能和速度之间最佳的平衡。局部加权技术,特别是
有趣的是,该方法没有使用具有均匀权重的方形窗口,而是让聚合窗口内的每个像素根据其颜色相似性和空间距离影响最终匹配成本,就像双边滤波一样(图12.10c)。实际上,他们的聚合步骤与对颜色/视差图像进行联合双边滤波密切相关,只是在参考图像和目标图像中都是对称进行的。汤巴里、马托奇亚和迪斯特凡诺(2007)提出的基于分割的聚合方法表现更好,尽管这种算法的快速实现尚未存在。另一种聚合方法是根据像素相似性沿一个或多个最小生成树进行聚合(杨2015;李、余等2017)。
在局部方法中,重点在于匹配成本计算和成本聚合步骤。计算最终的视差是简单的:只需在每个像素处选择与最小成本值相关的视差。因此,这些方法在每个像素处执行局部“胜者全得”(WTA)优化。这种方法(以及许多其他对应算法)的一个局限性是,匹配的独特性仅在一个图像(参考图像)中得到保证,而另一图像中的点可能与多个点匹配,除非
采用交叉检查和后续的孔洞填充(Fua1993;Hirschm ller和Scharstein
2009).
大多数立体对应算法在某种离散空间中计算一组视差估计值,例如整数视差(例外包括连续优化技术,如光流(Bergen,Anandan等1992)或样条(Szeliski和Coughlan 1997))。对于机器人导航或人员跟踪等应用,这些方法可能已经足够。然而,在基于图像的渲染中,这种量化地图会导致非常不吸引人的视图合成结果,即场景看起来由许多薄剪切层组成。为了改善这种情况,许多算法在初始离散对应阶段之后应用亚像素细化阶段。(另一种方法是从一开始就使用更离散的视差级别(Szeliski和Scharstein 2004)。)
亚像素视差估计可以通过多种方法计算,包括迭代梯度下降和在离散视差水平上拟合曲线(Ryan、Gray和Hunt 1980;Lucas和Kanade 1981;Tian和Huhns 1986;Matthies、Kanade和Szeliski 1989;Kanade和Okutomi 1994)。这提供了一种简单的方法,在不增加大量额外计算的情况下提高立体算法的分辨率。然而,为了有效工作,匹配的强度必须平滑变化,且这些估计计算区域必须位于同一(正确的)表面上。
关于拟合相关曲线的可取性,已经提出了一些问题
整数采样匹配成本(Shimizu和Okutomi2001)。当使用采样不敏感的差异度量时,这种情况甚至可能更糟(Birchfield和Tomasi 1998)。这些问题由Szeliski和Scharstein(2004)和Haller和Nedevschi(2012)进行了更深入的探讨。
除了子像素计算外,还有其他方法可以对计算出的视差进行后处理。可以通过交叉检查来检测遮挡区域,即比较左到右和右到左的视差图(Fua1993)。可以应用中值滤波器来清理虚假的不匹配,由于遮挡导致的空洞可以通过表面拟合或分配邻近视差估计来填补(Birchfield和Tomasi1999;Scharstein1999;Hirschm ller和Scharstein2009)。
另一种后处理方法,在后续处理阶段可能非常有用,是将置信度与逐像素深度估计(Figure12.11)关联起来。这可以通过观察相关曲面的曲率来实现,即在获胜视差处,DSI图像中的最小值有多强。Matthies、Kanade和Szeliski(1989)表明,在假设噪声较小、光度校准图像和密集采样的视差的情况下,局部深度估计的方差可以被估算为
(12.6)
其中a是DSI作为d的函数的曲率,可以使用局部方法来测量
抛物线拟合或通过平方窗口中的所有水平梯度,σ是变数-
图像噪声的强度可以通过最小SSD分数来估计。(参见第8.1.4节,(9.37),以及附录B.6。)多年来,提出了多种立体置信度测量方法。Hu和Mordohai(2012)及Poggi、Kim等人(2021)对此主题进行了详尽的综述。
实时立体算法的一个常见应用是跟踪用户与计算机或游戏系统互动的位置。使用立体技术可以显著提高此类系统的可靠性,相比之下,仅使用单目颜色和强度信息则效果较差(Darrell,Gordon等,2000)。一旦恢复这些信息,它们可以在多种应用中发挥作用,包括控制虚拟环境或游戏、在视频会议中校正视线方向以及背景替换。我们将在下文讨论前两个应用,并将背景替换的讨论推迟到第12.5.3节。
在计算机显示器上观看3D物体或环境时,使用头部跟踪来控制用户的虚拟视点有时被称为鱼缸虚拟现实,因为

图12.11立体深度估计的不确定性(Szeliski1991b):(a)输入图像;(b)估计的深度图(蓝色更近);(c)估计的置信度(红色更高)。如您所见,纹理区域的置信度更高。
用户仿佛置身于鱼缸中观察一个三维世界(Ware,Arthur,和Booth 1993)。早期版本的系统使用机械头部追踪设备和立体眼镜。如今,这些系统可以通过基于立体声的头部追踪来控制,而立体眼镜则被自动立体显示器所取代。头部追踪还可以用于构建“虚拟镜子”,用户可以通过各种视觉效果实时修改自己的头部(Darrell,Baker等1997)。
立体头追踪和三维重建的另一个应用是在注视校正(Ott,Lewis,和Cox 1993)。当用户参与桌面视频会议或视频聊天时,摄像头通常放置在显示器上方。由于人的眼睛注视着屏幕上的某个窗口,看起来像是他们向下看,而不是直接看向其他参与者。用两个或更多摄像头替换单个摄像头,可以在他们注视的位置构建虚拟视角,从而实现虚拟眼神交流。实时立体匹配用于构建精确的三维头部模型,视图插值(第14.1节)用于合成新的中间视图(Criminisi,Shotton等2003)。关于视频会议中注视校正的更近期出版物包括Kuster,Popa等(2012)和Kononenko和Lempitsky(2015),以及
12.5 全球优化
全局立体匹配方法在视差计算阶段之后执行一些优化或迭代步骤,并且通常完全跳过聚合步骤,因为全局平滑约束具有类似的功能。许多全局方法是在能量最小化框架下构建的,在第4章(4.24–4.27)和第9章中我们看到,目标是找到一个解d,使全局能量最小化。
E (d) = ED (d) + λES (d). (12.7)
数据项ED (d)衡量了视差函数d与输入图像对的吻合程度。利用我们先前定义的视差空间图像,我们将这种能量定义为
(12.8)
其中C是(初始或聚合)匹配成本DSI。
平滑项ES (d)编码了算法所做出的平滑假设。为了使优化在计算上可行,平滑项通常仅限于测量相邻像素差异之间的差异,
其中P是视差差异的单调递增函数。也可以使用更大的邻域,例如N8,这可以产生更好的边界(Boykov和Kolmogorov 2003),或者使用二阶平滑项(Woodford、Reid等人2008),但这些项需要更复杂的优化技术。平滑函数的一个替代方案是使用低维表示,如样条(Szeliski和Coughlan 1997)。
在标准正则化(第4.2节)中,P是一个二次函数,这使得d在所有地方都是平滑的,但在物体边界处可能导致结果不佳。没有这个问题的能量函数被称为不连续性保持型,并基于稳健的P函数(Terzopoulos 1986b;Black和Rangarajan 1996)。Geman和Ge- man(1984)的开创性论文给出了这些能量函数的贝叶斯解释,并提出了一种基于马尔可夫随机场(MRFs)和附加线过程的不连续性保持型能量函数,这些附加的二进制变量控制是否施加平滑惩罚。Black和Rangarajan(1996)展示了如何用稳健的成对差异项替代独立线过程变量。
PD(d(x,y)—d(x + 1,y))·PI(ⅡI(x,y)—I(x + 1,y)Ⅱ), (12.10)
其中PI是强度差异的单调递减函数,在高强度梯度下降低平滑成本。这一想法(Gamble和Poggio 1987;Fua 1993;Bobick和Intille 1999;Boykov、Veksler和Zabih 2001)鼓励视差不连续性与强度或颜色边缘相吻合,并似乎解释了全局优化方法的一些良好性能。尽管大多数研究人员是启发式地设置这些函数,但Pal、Weinman等人(2012)展示了如何从真实视差图中学习此类条件随机场中的自由参数(第4.3节,(4.47))。
一旦定义了全局能量,可以使用多种算法来找到(局部)最小值。与正则化和马尔可夫随机场相关的传统方法包括连续法(Blake和Zisserman 1987)、模拟退火法(Geman和Geman 1984;Marroquin、Mitter和Poggio 1987;Barnard 1989)、最高置信度优先法(Chou和Brown 1990)以及平均场退火法(Geiger和Girosi 1991)。
最大流和图割方法已被提出用于解决一类特殊的全局优化问题(Roy和Cox 1998;Boykov、Veksler和Zabih 2001;Ishikawa 2003)。这些方法比模拟退火更高效,并且已经取得了良好的结果,基于循环信念传播的技术也是如此(Sun、Zheng和Shum 2003;Tappen和Freeman 2003)。附录B.5和关于MRF推理的综述论文(Szeliski、Zabih等2008;Blake、Kohli和Rother 2011;Kappes、Andres等2015)详细讨论并比较了这些技术。
尽管对于KITTI等具有大量训练图像和与测试分布高度重叠的数据集,深度学习方法(第12.6节)在很大程度上取代了全局优化技术,但它们在具有挑战性的立体对上仍然表现最佳
包括高分辨率的米德尔伯里对(Scharstein,Hirschm ller等人)等细节。
2014)。Taniai、Matsushita等人(2018)开发的局部扩展移动算法就是这种做法的一个例子。下面,我们描述一些具有历史意义、运行速度更快或专门用于处理特定情况的相关技术。
协同算法。受人类立体视觉计算模型启发的协同算法,是最早提出用于视差计算的方法之一(Dev 1974;Marr和Poggio 1976;Marroquin 1983;Szeliski和Hinton 1985;Zitnick和Kanade 2000)。这些算法通过基于邻近视差和匹配值的非线性操作迭代更新视差估计,其整体行为类似于全局优化算法。事实上,对于某些算法,可以明确地表述一个正在最小化的全局函数(Scharstein和Szeliski 1998)。

图12.12使用局部平面扫描进行立体匹配(Sinha、Scharstein和Szeliski
2014)©2014 IEEE:(a)输入图像;(b)初始稀疏匹配;(c)按倾斜平面分组的匹配;(d)平面和分组特征的3D可视化。
也是迭代算法,这些算法会查看图像中的较大邻域,例如Patch- Match Stereo (Bleyer、Remann和Rother 2011),该方法在每个像素处估计一个局部三维平面,并使用非局部Patch- Match算法(Barnes、Shechtman等2009)快速找到平面上的大致最近邻。这种方法最近被应用于多视图立体设置中,生成了一个极其高效且高质量的算法(Wang、Galliani等2021)。
粗到精和增量变形。当今大多数最佳算法首先枚举所有可能的匹配点及其所有可能的视差,然后以某种方式选择最佳匹配集。有时可以使用受经典(无穷小)光流计算启发的方法获得更快的处理速度。在此过程中,图像依次进行变形,视差估计逐步更新,直到达到满意的配准效果。这些技术通常在一个粗到精的层次细化框架内实现(Quam 1984;Bergen,Anandan等1992;Barron,Fleet和Beauchemin 1994;Szeliski和Coughlan 1997)。最近,粗到精或金字塔方法在现代深度网络中重新兴起,既应用于光流(Ranjan和Black 2017;Sun,Yang等2018),也应用于立体视觉(Chang和Chen 2018)。
局部平面扫描。除了垂直于观察方向的平面扫描外,还可以使用一组倾斜平面来建模场景,这在场景包含高度倾斜的平面表面如地板或墙壁时尤为有利,如图12.12所示(Sinha,Scharstein和Szeliski 2014)。一旦估计出这些平面并分配给每个平面的像素,就可以估算每个像素的平面外位移,以更好地建模曲面。倾斜平面在PatchMatch立体算法中也曾被使用过(Bleyer,Rhemann和Rother 2011),并且最近也在用于智能手机AR的平面双边求解器中得到了应用(Valentin,Kowdle等2018)。

图12.13使用动态规划进行立体匹配,如(a) Scharstein和Szeliski(2002)©2002斯普林格出版社和(b) Kolmogorov、Criminisi等人(2006)©2006 IEEE所展示。对于每对对应的扫描线,选择一条通过所有成对匹配成本矩阵(DSI)的最小路径。小写字母(a–k)表示沿每条扫描线的强度。大写字母代表通过矩阵的选择路径。匹配点用M表示,而部分遮挡点(具有固定成本)则用L或R表示,分别对应仅在左图像或右图像中可见的点。通常,只考虑有限的视差范围(图中为0–4,用未加阴影的方块表示)。(a)中的表示允许对角线移动,而(b)中的表示不允许。请注意,这些图使用了深度的独眼巨人表示法,即相对于两台输入相机之间的相机的深度,显示了DSI的“未偏斜”的x轴切片。
一类不同的全局优化算法基于动态规划。虽然对于常见的平滑函数类,方程(12.7)的二维优化可以证明是NP难的(Veksler1999),但动态规划可以在多项式时间内找到独立扫描线的全局最小值。动态规划最初用于稀疏、基于边缘的方法中的立体视觉(Baker和Binford1981;Ohta和Kanade 1985)。最近的方法则集中在密集(基于强度)的扫描线匹配问题上(Belhumeur1996;Geiger、Ladendorf和Yuille1992;Cox、Hingorani等人1996;Bobick和Intille1999;Birchfield和Tomasi1999)。这些方法通过计算两个对应扫描线之间所有成对匹配成本矩阵中的最小代价路径来工作,即通过DSI的一个水平切片。部分遮挡通过将一个图像中的像素组分配给另一个图像中的单个像素来显式处理。

图12.13示意性地显示了DP的工作原理,而图12.5f显示了应用DP的实DSI切片。
为了对扫描线y实施动态规划,二维成本矩阵D(m,n)中的每个条目(状态)通过结合其DSI匹配成本值与其前驱成本值之一,并同时包括遮挡像素的固定惩罚来计算。图12.13b所示的聚合规则由Kolmogorov、Criminisi等人(2006)给出,他们还使用了两态前景-背景模型进行双层分割。
动态规划立体问题包括选择正确的遮挡像素成本以及难以实现扫描线间的连贯性,尽管有几种方法提出了解决后者的方法(Ohta和Kanade 1985;Belhumeur 1996;Cox、Hingorani等1996;Bobick和Intille 1999;Birchfield和Tomasi 1999;Kolmogorov、Criminisi等2006)。另一个问题是动态规划方法需要强制单调性或排序约束(Yuille和Poggio 1984)。这一约束要求两个视图之间扫描线上的像素相对顺序保持不变,但在包含狭窄前景物体的场景中可能不成立。
一种替代传统动态规划的方法,由Scharstein和Szeliski(2002)提出,是忽略公式(12.9)中的垂直平滑约束,直接在全局能量函数(12.7)中优化独立的扫描线。这种扫描线优化算法的优点在于它计算出相同的表示,并且最小化了与完整二维能量函数(12.7)相同的能量函数的简化版本。不幸的是,它仍然存在与动态规划相同的条纹伪影问题。动态规划也可以应用于树结构,这可以改善条纹现象(Veksler2005)。
通过从多个方向,例如,从八个基本方向N、E、W、S、NE、SE、SW,来求和累积成本函数,可以获得更高质量的结果,
NW(Hirschm ller2008)。由此产生的半全局匹配(SGM)算法执行
表现良好且极其高效,能够实现实时低功耗应用(Gehrig,Eberli,和Meyer 2009)。Drori、Haubold等人(2014)指出,SGM在特定的信念传播变体中等同于提前停止。半全局匹配也通过学习组件得到了扩展,例如SGM-Net (Seki和Pollefeys 2017),该方法使用卷积神经网络调整转换成本;以及SGM-Forest (Sch nberger,Sinha,和Pollefeys 2018),该方法利用随机森林分类器融合来自不同方向的视差提议。
虽然大多数立体匹配算法以每个像素为基础进行计算,但一些技术首先将图像分割成区域,然后尝试给每个区域贴上视差。

图12.14基于分割的立体匹配(Zitnick,Kang等人,2004)©2004
ACM: (a)输入彩色图像;(b)基于颜色的分割;(c)初始视差估计;(d)最终分段平滑视差;(e)在视差空间分布中定义的MRF邻域(Zitnick和Kang 2007)©2007斯普林格。

图12.15自适应过度分割和遮罩的立体匹配(田口、威尔伯恩和齐特尼克2008)©2008 IEEE:在优化过程中细化了段边界,从而获得更准确的结果(例如,底部行中的细绿色叶);(b)在段边界处提取了alpha遮罩,这使得合成效果更加美观(中间列)。
例如,陶、索尼和库马尔(2001)对参考图像进行分割,使用局部技术估计每个像素的视差,然后在每个分割内进行局部平面拟合,之后在相邻分割之间应用平滑约束。齐特尼克、康等人(2004)和齐特尼克与康(2007)采用过度分割来缓解初始不良分割。在将每个分割的一组初始成本值存储到视差空间分布(DSD)后,通过迭代松弛(或在齐特尼克和康(2007)的最新工作中称为循环信念传播)调整每个分割的视差估计值,如图12.14所示。田口、威尔伯恩和齐特尼克(2008)在优化过程中细化分割形状,从而显著改善了结果,如图12.15所示。
克劳斯、索曼和卡纳(2006)通过首先使用均值漂移对参考图像进行分割,然后运行一个小的(3×3) SAD加梯度SAD(通过交叉验证加权),以获得初始视差估计,拟合局部平面,再用全局平面重新拟合,最后在平面分配上运行最终的MRF并采用循环信念传播。

图12.16使用边缘、平面和超像素的多帧匹配(Xue,Owens等人,2019)©2019 Elsevier。
当该算法在2006年首次引入时,它是现有米德尔伯里基准上的排名最高的算法。
王和郑(2008)的算法采用了类似的分割图像的方法,进行局部平面拟合,然后对邻近平面拟合参数进行协同优化。杨、王等人(2009)的算法则利用尹和奎恩(2006)的颜色相关方法和层次信念传播来获得初始的一组视差估计。加尔普、弗拉姆和波莱菲斯(2010)将图像分割为平面区域和非平面区域,并使用不同的表示方法处理这两类表面。
最近,Xue、Owens等人(2019)首先匹配多帧立体序列中的边缘,然后拟合重叠的方形补丁以获得局部平面假设。然后使用超像素和最终的边缘感知松弛来细化这些假设,以获得连续的深度图。
基于分割的立体算法还具备一种重要的能力,即在深度不连续处提取分数像素透明度(Bleyer,Gelautz等2009)。这一能力对于尝试创建虚拟视图插值时至关重要,可以避免边界粘连或撕裂伪影(Zitnick,Kang等2004),同时也能无缝插入虚拟对象(Taguchi,Wilburn,和Zitnick 2008),如图Figure12.15b所示。
实时立体匹配的另一个应用是z键,这是利用深度信息将前景演员从背景中分割出来的过程,通常是为了用一些计算机生成的图像替换背景,如图所示

图12.17使用z键替换背景,采用abi层分割算法(Kolmogorov,Criminisi等人,2006)©2006 IEEE。
图12.2g。
最初,Z键系统需要昂贵的定制硬件来实时生成所需的深度图,因此仅限于广播工作室应用(Kanade,Yoshida等1996;Iddan和Yahav 2001)。离线系统也被开发用于从视频流中估计三维多视角几何(第14.5.4节)(Kanade,Rander和Narayanan 1997;Carranza,Theobalt等2003;Zitnick,Kang等2004;Vedula,Baker和Kanade 2005)。高度准确的实时立体匹配随后使得在普通个人电脑上执行Z键成为可能,从而支持如图12.17所示的桌面视频会议应用(Kolmogorov,Criminisi等2006),但这些应用大多已被用于背景替换的深度网络所取代(Sengupta,Jayaram等2020)以及用于增强现实的实时3D手机重建算法(图11.28和Valentin,Kowdle等2018)。
12.6 深度神经网络
与其他计算机视觉领域一样,深度神经网络和端到端学习对立体匹配产生了巨大影响。在本节中,我们将简要回顾深度神经网络在立体对应算法中的应用。我们遵循Poggi、Tosi等人(2021)和Laga、Jospin等人(2020)最近两篇综述的结构,将技术分为三类,即,
1.立体管道中的学习,
2.使用2D架构进行端到端学习,以及
我们简要讨论了每组中的几篇论文,并建议读者阅读完整的调查以了解更多信息
详情(Janai,G等人,2020;Poggi,Tosi等人,2021;Laga,Jospin等人,2020)。
立体管道中的学习
甚至在深度学习出现之前,一些作者就提出了学习传统立体管道组件的方法,例如,学习MRF和CRF立体模型的超参数
(Zhang和Seitz2007;Pal,Weinman等人2012)。bontar和LeCun(2016)是
首先通过训练特征优化成对匹配成本,将深度学习引入立体视觉。这些学到的匹配成本至今仍广泛应用于中伯里立体评估中的顶尖方法。此后,许多其他作者提出了用于匹配成本计算和聚合的卷积神经网络(Luo,Schwing和Urtasun 2016;Park和Lee 2017;Zhang,Prisacariu等2019)。
学习也被用于改进传统的优化技术,特别是
广泛使用的Hirschm ller(2008)的SGM算法。这包括SGM-Net (Seki和
Pollefeys2017)使用卷积神经网络调整过渡成本,SGM-Forest(Sch nberger,Sinha,和Pollefeys2018)则使用随机森林分类器从多个入射方向选择视差值。卷积神经网络还被用于细化阶段,取代了早期的技术如双边滤波(Gidaris和Komodakis2017;Batsos和Mordohai2018;Kn belreiter和Pock2019)。
使用2D架构的端到端学习
大型合成数据集及其真实差异的可用性,特别是弗赖堡场景流数据集(Mayer,Ilg等,2016,2018),使得立体网络能够进行端到端训练,并催生了大量新方法。这些方法在提供足够训练数据的基准测试中表现良好,使网络可以针对特定领域进行调整,特别是在KITTI(Geiger,Lenz和Urtasun,2012;Geiger,Lenz等,2013;Menze和Geiger,2015)中,基于深度学习的方法自2016年起开始主导排行榜。
最早的用于立体视觉的深度学习架构与设计用于密集回归任务如语义分割的架构相似(陈、朱等人,2018)。这些二维架构通常采用受U-Net启发的编码器-解码器设计(罗内伯格、菲舍尔和布罗克斯,2015)。首个此类模型是DispNet-C,由梅耶、伊尔格等人在开创性论文中提出(2016),利用相关层(多索维茨基、菲舍尔等人,2015)计算图像层之间的相似度。

图12.18由三种不同DNN立体匹配器计算的差异图,这些匹配器在合成数据上训练,并应用于真实图像对(Zhang,Qi等人,2020)©2020 Springer。
后续对2D架构的改进包括残差网络的概念,该网络对原始视差进行残差校正(Pang,Sun等2017),也可以采用迭代方式实现(Liang,Feng等2018)。可以使用粗到精的处理方法(Tonioni,Tosi等2019;Yin,Darrell,和Yu 2019),网络可以估计遮挡和深度边界(Ilg,Saikia等2018;Song,Zhao等2020)或使用神经架构搜索(NAS)来提高性能(Saikia,Marrakchi等2019)。HITNet结合了这些想法中的多个,并通过局部倾斜平面假设和迭代优化,产生了高效且最先进的结果(Tankovich,Hane等2021)。
由Kn belreiter、Reinbacher等人(2017)开发的2D架构使用联合
卷积神经网络和条件随机场(CRF)模型来推断密集视差图。另一种有前景的方法是多任务学习,例如,同时估计视差和语义分割(Yang、Zhao等人2018;Jiang、Sun等人2019)。通过将输出表示为双峰混合分布,还可以提高输出深度图的表观分辨率并减少过度平滑(Tosi、Liao等人2021)。
使用3D架构进行端到端学习
一种替代方法是使用三维架构,该架构通过处理三维体积中的特征来显式编码几何信息,其中第三个维度对应于视差搜索范围。换句话说,这种架构显式表示了视差空间图像(DSI),同时仍然保留多个特征通道,而不仅仅是标量成本值。与二维架构相比,它们需要更高的内存需求和运行时间。
此类架构的首批实例包括GC-Net(Kendall,Martirosyan等人,2017)和PSMNet (Chang和Chen,2018)。3D架构还允许整合传统的局部聚合方法(Zhang,Prisacariu等人,2019)和避免方法。
几何不一致(Chabra,Straub等,2019)。尽管资源限制通常意味着基于3D DNN的立体方法在较低分辨率下运行,但层次立体匹配(HSM)网络(Yang,Manela等,2019)采用金字塔方法,在较高分辨率下选择性地限制搜索空间,并支持随时按需推理,即在较高帧率下提前停止处理。Duggal,Wang等(2019)通过在循环神经网络中开发可微版本的PatchMatch(Bleyer,Rheumann和Rother,2011),解决了资源有限的问题。Cheng,Zhong等(2020)利用神经架构搜索(NAS)创建了最先进的3D架构。
虽然监督深度学习方法已经主导了包括KITTI等专用训练集在内的各个基准测试,但它们在不同领域中的泛化能力仍然不足(Zendel等人,2020)。在米德尔伯里基准测试中,该测试以高分辨率图像为主,并且仅提供非常有限的训练数据,深度学习方法仍然明显缺失。Poggi、Tosi等人(2021)指出了以下两个主要挑战:(1)跨不同领域的泛化,以及(2)在高分辨率图像上的应用。对于跨领域泛化,Poggi、Tosi等人(2021)描述了离线和在线自监督适应及引导深度学习的技术,而Laga、Jospin等人(2020)则讨论了微调和数据转换。一个最近的领域泛化示例是张、Qi等人(2020)提出的域不变立体匹配网络(DSMNet),其表现优于其他最先进的模型,如HD3 (Yin、Darrell和Yu 2019)和PSMNet (Chang和Chen 2018),如图12.18所示。另一个领域适应的例子是AdaStereo(Song、Yang等人,2021)。对于高分辨率图像,已经开发出技术以粗到精的方式提高分辨率(Khamis、Fanello等人,2018;Chabra、Straub等人,2019)。
12.7 多视图立体
虽然匹配图像对是获取深度信息的有效方法,但使用更多图像可以显著提高效果。在本节中,我们不仅回顾了创建完整3D物体模型的技术,还介绍了利用多源图像改善深度图质量的简单技术。关于截至2015年开发的技术的良好综述可以在Furukawa和Hern ndez(2015)中找到,而更近期的综述则可以在
Janai、G等(2020,第10章)。
正如我们在讨论平面扫描(第12.1.2节)时所见,可以在每个视差假设d下,将所有相邻的k张图像重新采样到一个广义视差空间体I(x,y,d,k)中。利用这些额外图像最简单的方法是求和。

图12.19极线平面图像(EPI)(Gortler,Grzeschuk等,1996)©1996 ACM和示意图EPI (Kang,Szeliski,和Chai,2001)©2001 IEEE。(a)光场图(Lumigraph)(第14.3节)是所有穿过空间体积的光线组成的四维空间。取二维切片结果是所有光线嵌入一个平面上,相当于从堆叠的EPI体积中获取的一条扫描线。不同深度的物体以与它们的倒数深度成比例的速度(斜率)横向移动。这种表示方式下可以轻松看到遮挡(和半透明)效果。(b)对应于图12.20的EPI显示了三个图像(中间、左和右)作为EPI体积的切片。黑色像素周围的时空偏移窗口用矩形标出,表明右侧图像未用于匹配。
将它们与参考图像Ir的差异如(12.4)所示,
(12.11)
这是著名的平方差总和(SSSD)和SSAD方法的基础(Okutomi和Kanade 1993;Kang、Webb等人1995),这些方法可以扩展到推断可能的遮挡模式(Nakamura、Matsuura等人1996)。Gallup、Frahm等人(2008)的最新研究展示了如何根据预期深度调整基线,以在几何精度(宽基线)和遮挡鲁棒性(窄基线)之间获得最佳平衡。替代的多视图成本度量包括合成焦点锐度和像素颜色分布的熵等指标(Vaish、Szeliski等人2006)。
一种有用的可视化多帧立体估计问题的方法是检查由所有图像中对应扫描线堆叠形成的极线平面图像(EPI),如图9.11c和12.19所示(Bolles,Baker,和Marimont 1987;Baker和Bolles 1989;Baker 1989)。从图12.19可以看出,当相机水平移动时(在

图12.20空间时间可移动窗口(Kang,Szeliski和Chai 2001)©2001 IEEE:一个简单的三帧序列(中间的图像作为参考图像),其中有一个移动的正面灰色方块(标记为F)和一个静止的背景。区域B、C、D和E部分被遮挡。(a)使用常规的SSD算法,在匹配这些区域的像素时(例如,以区域B中的黑色像素为中心的窗口)以及跨越深度不连续性的窗口中(以区域F中的白色像素为中心的窗口),会出错。(b)可移动窗口有助于缓解部分遮挡区域和接近深度不连续性的问题。以区域F中的白色像素为中心的移动窗口在所有帧中都能正确匹配。以区域B中的黑色像素为中心的移动窗口在左图中能正确匹配,但在右图中需要时间选择来禁用匹配。图12.19b显示了与该序列相对应的EPI,并详细描述了时间选择的工作原理。
标准水平校正几何),不同深度的物体以与其深度成反比的速度横向移动(12.1)。前景物体遮挡背景物体,这些背景物体可以被视为EPI条带(Criminisi,Kang等,2005)遮挡其他条带。如果我们有一组足够密集的图像,我们可以找到这样的条带,并推断它们之间的关系,从而重建三维场景并推断半透明物体(Tsin,Kang,和Szeliski,2006)和镜面反射(Swaminathan,Kang等,2002;Criminisi,Kang等,2005)。或者,我们可以将这组图像视为一系列连续的观测,并使用卡尔曼滤波(Matthies,Kanade,和Szeliski,1989)或最大似然推断(Cox,1994)进行合并。
当可用图像较少时,有必要采用聚合技术,如滑动窗口或全局优化。然而,随着输入图像的增加,遮挡的可能性也随之增加。因此,不仅应使用可移动窗口方法调整最佳窗口位置,如图12.20a所示,还应选择邻近帧的一个子集来排除那些感兴趣区域被遮挡的图像,如图12.20b所示(Kang,Szeliski,和Chai 2001)。图-
7 EPI的四维推广是光场,我们在第14.3节中研究了它。

图12.21局部(基于5×5窗口)匹配结果(Kang、Szeliski和Chai
2001)©2001 IEEE:不受空间扰动的窗口(居中);(b)受空间扰动的窗口;(c)使用十个相邻帧中的最佳五个;(d)使用较好的一半序列。请注意,使用时间选择后,靠近树干的结果得到了改善。
图12.19b显示了这种时空选择或窗口移动如何对应于在极线平面图像体积中选择最可能的未被遮挡的体积区域。
图12.21展示了将这些技术应用于多帧花园区图像序列的结果,比较了使用常规(未移位)SSSD与空间移位窗口以及全时空窗口选择的结果。(将立体视觉应用于用移动摄像机拍摄的刚性场景有时称为运动立体)。Kang和Szeliski(2004)报告了使用时空选择带来的类似改进,即使在局部测量与全局优化结合时也显而易见。
虽然从多个输入计算深度图优于成对立体匹配,但通过同时估计多个深度图可以获得更显著的改进(Szeliski1999a;Kang和Szeliski2004)。多张深度图的存在使得关于遮挡的推理更加准确,因为在一张图像中被遮挡的区域可能在其他图像中可见(且可匹配)。多视图重建问题可以表述为在关键帧处同时估计深度图(图9.11c),不仅最大化照片一致性和平滑的分段视差,还要保证不同帧之间视差估计的一致性。尽管Szeliski(1999a)和Kang与Szeliski(2004)使用软(基于惩罚)约束来鼓励多个视差图的一致性,Kolmogorov和Zabih(2002)展示了如何将这种一致性度量编码为硬约束,以确保多个深度图不仅相似,而且在重叠区域实际上是相同的。同时估计多个视差图的其他算法包括Maitre、Shinagawa和Do(2008)以及Zhang、Jia等人(2008)的算法,以及广泛使用的COLMAP算法(Sch nberger、Zheng等人2016),该算法通过视图选择和多张深度图之间的几何一致性来过滤匹配,如图12.26b所示。
最新的多视图立体算法使用深度神经网络来计算匹配

图12.22使用三种不同的多视图立体算法计算的深度图,如彩色点云所示(Yao,Luo等人,2018)©2018 Springer。红色框表示MVSNet表现更好的问题区域。
(成本)体积并将其融合成差异图。DeepMVS系统计算参考图像与邻近图像之间的两两匹配成本,然后通过最大池化将它们融合在一起,随后进行密集CRF优化(Huang,Matzen等,2018)。MVSNet计算所有编码图像在每个扫描平面上的差异,使用3D U-Net正则化这些成本,再通过软argmin和深度优化网络,在DTU和坦克与寺庙数据集上产生良好结果(Yao,Luo等,2018),如图12.22所示。
最近的此类网络变体包括P-MVSNet (Luo,Guan等,2019),该方法使用逐块匹配置信度聚合器;以及CasMVSNet(Gu,Fan等,2020)和CVP-MVSNet(Yang,Mao等,2020),两者均采用粗到精的金字塔处理。四篇更为近期的论文在DTU、ETH3D、Tanks and Temples和/或Blended MVS数据集上表现优异,分别是Vis-MVSNet(Zhang,Yao等,2020)、D2HC-RMVSNet(Yan,Wei等,2020)、DeepC-MVS(Kuhn,Sormann等,2020)和PatchmatchNet (Wang,Galliani等,2021)。这些算法结合了可见性和遮挡推理、置信度或不确定性图以及几何一致性检查,并采用了高效的传播方案以取得良好效果。随着越来越多的新多视图立体论文不断发表,ETH3D和Tanks and Temples排行榜(表12.1)是
12.7.1场景流
与多帧立体估计密切相关的一个主题是场景流,其中使用多个摄像头捕捉动态场景。任务是在每一刻同时恢复物体的三维形状,并估计每帧之间每个表面点的完整三维运动。该领域的代表性论文包括Vedula、Baker等人(2005),

图12.23三维场景流:(a)由围绕舞者的多摄像头穹顶计算得出,如图12.2h-j所示(Vedula,Baker等人,2005)©2005 IEEE;(b)由安装在移动车辆上的立体相机计算得出(Wedel,Rabe等人,2008)©2008 Springer。
Zhang和Kambhamettu(2003)、Pons、Keriven和Faugeras(2007)、Huguet和Devernay
(2007)、Wedel、Rabe等人(2008)和Rabe、M ller等人(2010)。图12.23a显示了一个-
图12.2h至j展示了探戈舞者在三维场景流中的年龄,而图12.23b则显示了为了避障从移动车辆中捕捉到的三维场景流。除了支持测量和安全应用外,场景流还可以用于空间和时间视图插值(第14.5.4节),这一点由Vedula、Baker和Kanade(2005)所证明。
KITTI场景流数据集的创建(Geiger,Lenz,和Urtasun 2012)以及自动驾驶兴趣的增加,加速了场景流算法的研究(Janai,G ney等2020,第12章)。一种帮助正则化问题的方法是采用分段平面表示(Vogel,Schindler,和Roth 2015)。另一种方法是将场景分解为刚性独立移动的对象,如车辆(Menze和Geiger 2015),使用语义分割(Behl,Hosseini Jafari等2017),以及其他分割线索(Ilg,Saikia等2018;Ma,Wang等2019;Jiang,Sun等2019)。3D传感器的更广泛可用性使得场景流算法能够扩展,利用这种模态作为额外输入(Sun,Sudderth,和Pfister 2015;
12.7.2体积和三维表面重建
最具挑战性但也最有用的多视图立体重建变体是构建全局一致的三维模型(Seitz,Curless等,2006)。这一主题在计算机视觉领域有着悠久的历史,始于表面网格重建技术,例如Fua和Leclerc(1995)开发的技术(图12.24a)。为了解决这个问题,人们采用了多种方法和表示形式,包括三维体素(Seitz和

图12.24多视图立体算法:(a)基于表面的立体(Fua和Leclerc 1995)©1995斯普林格;(b)体素着色(Seitz和Dyer 1999)©1999斯普林格;(c)深度图合并(Narayanan、Rander和Kanade 1998)©1998 IEEE;(d)水平集演化(Faugeras和Keriven 1998)©1998 IEEE;(e)线条和立体融合(Hern ndez和Schmitt 2004)©2004埃尔斯维尔;(f)多视图图像匹配(Pons、Keriven和Faugeras 2005)©2005 IEEE;(g)体积图割(Vogiatzis、Torr和Cipolla 2005)©2005 IEEE;(h)刻划视觉壳体(Furukawa和Ponce 2009)©2009斯普林格。
Dyer1999;Szeliski和Golland1999;De Bonet和Viola1999;Kutulakos和Seitz2000;Eisert、Steinbach和Girod2000;Slabaugh、Culbertson等人2004;Sinha和Pollefeys 2005;Vogiatzis、Hern和Diaz等人2007;
Hiep、Keriven等人2009),水平集(Faugeras和Keriven1998;Pons、Keriven和Faugeras2007),多边形网格(Fua和Leclerc1995;Narayanan、Rander和Kanade1998;Hern和Schmitt2004;Furukawa
和Ponce 2009),以及多个深度图(Kolmogorov和Zabih2002)。图12.24展示了使用这些技术重建的3D物体模型的一些代表性示例。
为了组织和比较所有这些技术,Seitz、Curless等人(2006)开发了一个六点分类法,可以帮助根据场景表示对算法进行分类,

图12.25多视图立体(a)场景表示和(b)处理管道,来自Furukawa和Hern ndez(2015)©2015现在出版商。
光一致性度量、可见性模型、形状先验、重建算法以及它们使用的初始化要求。下面,我们总结了其中的一些选择,并列出了一些代表性论文。如需更多详细信息,请参阅完整的综述文章(Seitz,Curless等2006)以及Furukawa和Ponce(2010)和Janai,G ney等(2020,第10章)的最新综述。ETH3D和Tanks and Temples的排行榜列出了最新的结果和近期论文的链接。
场景表示。根据福川和庞斯(2010)提出的分类法,多视图立体算法主要使用四种场景表示,即深度图、点云、体场和三维网格,如图12.25a所示。这些通常被整合成一个完整的流程,包括相机姿态估计、每张图像的深度图或点云计算、体融合以及表面网格细化(波莱菲斯、尼斯特等人,2008),如Figure12.25b所示。
我们已经在本节前面讨论过多视图深度图估计。一个点云表示的例子是Furukawa和Ponce(2010)开发的基于补丁的多视图立体(PMVS)算法,该算法从稀疏的三维点重建开始

图12.26点云重建:(a)PMVS管道,显示一个样本输入图像、检测到的特征、初始重建的补丁、扩展和过滤后的补丁以及最终的网格模型(Furukawa和Ponce2010)©2010 IEEE;(b)深度地图和
来自COLMAP多视图立体管道两个阶段的表面法线(Sch nberger,
Zheng等人,2016)©2016 Springer;(c)从密集的梯度中恢复出薄结构
轨道摄像机光场(Y cer,Kim等人,2016)©2016 IEEE。
利用运动结构,然后优化并密集化局部定向补丁或表面像素(Szeliski和Tonnesen 1992;第13.4节),同时考虑可见性约束,如图12.26a所示。这种表示可以转换为网格以进行最终优化。此后,改进了视图选择和过滤以及法线估计的技术,例如Fuhrmann和Goesele(2014)以及Sch nberger、Zheng等人(2016)开发的系统,后者(见图11.20b和12.26b)提供了流行的COLMAP开源重建系统的密集多视图立体组件(Sch nberger和Frahm 2016)。当有高采样率的视频序列时,可以从跟踪
边缘重建点云。
如第12.2.1节Kim、Zimmer等人(2013)和Y cer所述,更合适,
Kim等人(2016)和Figure12.26c中所示。
一种较为流行的三维表示方法是均匀的三维体素网格,可以使用多种雕刻技术(Seitz和Dyer 1999;Kutulakos和Seitz 2000)或优化方法(Sinha和Pollefeys 2005;Vogiatzis、Hern和其他2007;Hiep、Keriven和其他2009;Jancosek和Pajdla 2011;Vu、Labatut
和其他2012)进行重建,其中一些方法如图12.24所示。水平集技术(第7.3.2节)同样基于均匀网格,但不是表示二进制占用图,而是表示到表面的有符号距离(Faugeras和Keriven 1998;Pons、Keriven和Faugeras 2007),这可以编码更精细的细节,并且还可以用于合并多个点云或范围数据扫描,这一点在第13.2.1节中进行了详细讨论。除了使用均匀采样的体积,后者最适合紧凑的三维对象外,还可以创建一个与输入图像相对应的视锥体,并以逆深度的形式采样z维,即一组共面相机的均匀视差(图14.7)。这种表示方法在Szeliski和Golland(1999)中被称为醋酸盐堆栈,在Zhou、Tucker等人(2018)中称为多平面图像。
多边形网格是另一种流行的表示方法(Fua和Leclerc 1995;Narayanan、Rander和Kanade 1998;Isidoro和Sclaroff 2003;Hern ndez和Schmitt 2004;Furukawa
和Ponce 2009;Hiep、Keriven等2009)。网格是计算机图形学中常用的表示方式,同时也便于计算可见性和遮挡。最后,正如我们在前一节讨论的那样,也可以使用多个深度图(Szeliski 1999a;Kolmogorov和Zabih 2002;Kang和Szeliski 2004)。许多算法还使用了多种表示方法,例如,它们可能首先计算多个深度图,然后将这些深度图合并成一个三维对象模型(Narayanan、Rander和Kanade 1998;Furukawa和Ponce 2009;Goesele、Curless和Seitz 2006;Goesele、Snavely等2007;Pollefeys、Nist r等2008;Furukawa、Curless等2010;Furukawa和Ponce 2010;Vu、Labatut等2012
;Sch nberger、Zheng等2016),如图Figure12.25b所示。
一个最近的系统将几种表示方法结合成一种可伸缩的分布式方法,可以处理包含数百张高分辨率图像的数据集
LTVRE Kuhn、Hirschm ller等人(2017)的多视图立体系统。该系统启动
用SGM(Hirschm ller2008)计算的成对差异图。这些深度估计-
使用学习到的立体误差模型,通过八叉树处理可变分辨率,然后根据可见性约束过滤冲突点,最后进行三角化,将伙伴与概率多尺度方法融合。图12.27显示了处理管道的示意图。
对于延伸至无穷的室外场景,空间倒置网格可能更可取(Slabaugh、Culbertson等人,2004;Zhang、Riegler等人,2020)。

图12.27 Kuhn、Hirschm ller等人(2017)的3D重建流程©2017
施普林格:(0)动态结构;(1)使用半全局匹配的立体匹配;(2)深度质量估计;(3)概率空间占用;(4+5)概率点优化和异常值过滤;(6)三角测量。图(4+5)和图(6)的图像一半采用纹理映射,另一半采用平面着色,以展示更多的表面细节。
光一致性度量。正如我们在(第12.3.1节)中讨论的那样,可以使用多种相似性度量来比较不同图像中的像素值,包括试图减少光照影响或对异常值不那么敏感的度量。在多视图立体中,算法可以选择直接在模型表面计算这些度量,即在场景空间中,或者将一个图像(或纹理模型)的像素值投影回另一个图像,即在图像空间中。(后者更接近贝叶斯方法,因为输入图像是对彩色3D模型的噪声测量。)当有物体几何信息时,例如其与每个相机的距离及其局部表面法线,可以用来调整计算中使用的匹配窗口,以考虑缩短和尺度变化(Goesele,Snavely等,2007)。
可见性模型。多视图立体算法相较于单深度图方法的一大优势在于其能够以原则性的方式推理可见性和遮挡。利用当前三维模型状态预测每张图像中哪些表面像素可见的技术(Kutulakos和Seitz 2000;Faugeras和Keriven 1998;Vogiatzis、Hern和其他2007;Hiep、Keriven等2009;Furukawa和Ponce 2010;Sch nberger、Zheng等2016)被归类
为使用几何可见性模型,在Seitz的分类体系中。
Curless等人(2006)提出,选择图像邻近子集以匹配的技术被称为准几何方法(Narayanan、Rander和Kanade 1998;Kang和Szeliski 2004;Hernandez和Schmitt
2004),而使用传统鲁棒相似性度量的技术则称为基于异常值的方法。尽管完整的几何推理是最合理且准确的方法,但其评估速度可能非常慢,并且依赖于当前表面估计质量的演变来预测可见性,这可能会成为一个先有鸡还是先有蛋的问题,除非采用保守假设,如Kutulakos和Seitz(2000)所做的一样。
形状先验。由于立体匹配通常约束不足,尤其是在纹理较少的区域,大多数匹配算法采用(无论是显式还是隐式)某种形式的形状预期先验模型。许多依赖优化的技术使用基于3D平滑度或面积的照片一致性约束,由于平滑表面有向内收缩的自然倾向,这通常会导致最小表面先验(Faugeras和Keriven 1998;Sinha和Pollefeys 2005;Vogiatzis、Hern和其他2007)。那些削减空间体积的方法通常在找到照片一致性解后就停止(Seitz和Dyer 1999;Kutulakos和Seitz 2000),这对应于最大表面偏差,即这些技术倾向于高估真实形状。最后,多深度图方法通常采用传统的基于图像的平滑度(正则化)约束。
高级形状先验也可以使用,例如曼哈顿世界假设,该假设认为大多数感兴趣的表面是轴对齐的(Furukawa,Curless等2009a,b),或以倾斜屋顶等相关的方向(Sinha,Steedly和Szeliski 2009;Osman Ulusoy,Black和Geiger 2017)。这些类型的建筑先验在第13.6.1节中详细讨论。还可以使用图像中的二维语义分割,例如墙、地面和植被类别,以在模型的不同区域应用不同种类的正则化和表面法线先验(H ne,Zach等2013)。
重建算法。实际的重建算法如何进行的细节是多视图立体算法中最大差异和最大创新的地方。
一些方法使用定义在三维照片一致性体积上的全局优化来恢复完整的表面。基于图割的方法使用多项式复杂度的二值分割算法来恢复定义在体素网格上的对象模型(Sinha和Pollefeys 2005;Vogiatzis、Hern ndez等2007;Hiep、Keriven等2009;Jancosek和Pajdla 2011;Vu、Labatut等2012)。水平集方法通过连续的
表面演化来找到势能表面配置空间中的良好最小值,因此需要一个相当好的初始化(Faugeras和Keriven 1998;Pons、Keriven,

图12.28体素着色(Seitz和Dyer 1999)©1999斯普林格和空间雕刻(Kutulakos和Seitz 2000)©2000斯普林格。(a-b):体素着色以相机从前到后的顺序扫过场景中的平面。(c-d):空间雕刻使用多个扫描方向来处理更一般的相机配置。
以及Faugeras2007)。为了使照片一致性体积有意义,需要以某种稳健的方式计算匹配成本,例如使用有限视图集或通过聚合多个深度图。
一种替代全局优化的方法是在计算照片一致性与可见性的同时遍历三维体积。Seitz和Dyer(1999)的体素着色算法执行从前到后的平面扫描。在每个平面上,任何具有足够照片一致性的体素都被标记为物体的一部分。源图像中相应的像素可以被“擦除”,因为它们已经被考虑在内,因此不会对进一步的照片一致性计算产生影响。(Szeliski和Golland(1999)使用了类似的方法,但没有从前到后的扫描顺序。)在无噪声和无重采样的条件下,生成的三维体积可以保证产生一个照片一致的三维模型,并且包含生成图像的真实三维物体模型(图12.28a–b)。
不幸的是,体素着色只有在所有摄像机位于扫描平面同一侧时才有效,而在一般的环形摄像机配置中这是不可能的。库图拉科斯和塞茨(2000)将体素着色推广到空间雕刻,其中满足体素着色约束的摄像机子集被迭代选择,并且三维体素网格沿着不同的轴交替被雕刻(图12.28c-d)。
另一种流行的多视图立体方法是首先独立计算多个深度图,然后将这些部分图合并成一个完整的3D模型。关于深度图合并的方法,在第13.2.1节中详细讨论,包括由Goesele、Curless和Seitz(2006)使用的带符号距离函数(Curless和Levoy 1996),以及由Goesele、Kazhdan、Bolitho和Hoppe(2006)使用的泊松表面重建法,
初始化要求。Seitz、Curless等人(2006)讨论的最后一个要素是不同算法所需的初始化程度各不相同。由于某些算法需要细化或发展一个粗略的三维模型,因此它们需要一个相对准确(或过完备)的初始模型,这通常可以通过从物体轮廓重建体积来获得,如第12.7.3节所述。然而,如果算法执行全局优化(Kolev、Klodt等人2009;Kolev和Cremers2009),这种对初始化的依赖就不是问题了。
实证评估。数据集和基准的广泛采用,使得过去二十年多视角重建技术取得了快速进展。表12.1列出了其中一些最常用且有影响力的数据库,图12.1、12.22和12.26展示了样本图像和/或结果。更多数据集的指向可以参见Mayer,Ilg。
et al.(2018),Janai,G ney等人(2020),Laga,Jospin等人(2020)和Poggi,Tosi等人。
(2021)。在ETH3D和Tanks and Temples基准测试的排行榜上通常可以找到最新的算法。
在许多情况下,对感兴趣对象进行前景背景分割是初始化或拟合三维模型的好方法(Grauman、Shakhnarovich和Darrell 2003;Vlasic、Baran等人2008),或者对多视图立体施加一组凸约束(Kolev和Cremers 2008)。多年来,已经开发出多种技术,从投影到三维的二进制轮廓的交集重建三维体积模型。所得模型称为视觉壳(有时也称为线壳),类似于点集的凸包,因为该体积相对于视觉轮廓最大,且表面元素与沿轮廓边界的方向线(线)相切(Laurentini 1994)。还可以使用多视图立体(Sinha和Pollefeys 2005)或通过分析投射阴影(Savarese、Andreetto等人2007)来雕刻更精确的重建。
一些技术首先用多边形表示每个轮廓,然后在三维空间中相交生成的多面锥区域,以产生多面体模型(Baumgart1974;Martin和Aggarwal1983;Matusik、Buehler和McMillan2001),这些模型随后可以使用三角样条进行细化(Sullivan和Ponce1998)。其他方法则使用基于体素的表示,通常编码为八叉树(Samet1989),因为这能提高空间-时间效率。图12.29a-b展示了一个三维八叉树的例子。

图12.29从二值轮廓中重建的体积八叉树(Szeliski1993)©
1993年爱思唯尔:(a)八叉树表示及其对应的(b)树结构;(c)转盘上物体的输入图像;(d)计算出的三维体积八叉树模型。
模型及其关联的彩色树,其中黑色节点表示模型内部,白色节点表示外部,灰色节点表示混合占用。基于八叉树的重建方法的例子包括Potmesil(1987)、Noborio、Fukada和Arimoto(1988)、Srivasan、Liang和Hackwood(1990)以及Szeliski(1993)。
斯泽利斯基(1993)的方法首先将每个二值轮廓转换为距离图的一种单边变体,其中图中的每个像素表示完全位于(或位于)轮廓内的最大正方形。这使得将八叉树单元投影到轮廓中以确认其是否完全位于物体内部或外部变得快速,从而可以将其着色为黑色、白色或保留为灰色(混合)以便在较小的网格上进一步细化。八叉树构建算法以粗到细的方式进行,首先在相对较低的分辨率下构建一个八叉树,然后通过重新访问和细分所有尚未确定占用情况的输入图像来细化灰色(混合)单元。图12.29d显示了从旋转盘上的咖啡杯计算出的结果八叉树模型。
最近关于视觉船体计算的研究借鉴了基于图像渲染的思想,因此被称为基于图像的视觉船体(Matusik,Buehler等,2000)。与预先计算全局三维模型不同,基于图像的视觉船体是针对每个新视角重新计算的,通过依次将视图光线段与二值轮廓相交来实现。

图12.30来自NYU深度数据集V2 (Wang,Geraghty等人,2020)的单目深度推断(以颜色编码的法线图显示)©2020 IEEE。
每个图像。这不仅导致了快速计算算法,而且能够使用来自输入图像的颜色值快速对恢复的模型进行纹理处理。这种方法还可以与高质量可变形模板结合,以捕捉和重新激活全身运动(Vlasic,Baran等人,2008)。
虽然上述方法以二值前景/背景轮廓图像为起点,但也可以提取出通常达到亚像素精度的轮廓曲线,并通过跟踪这些曲线来重建部分表面网格,如第12.2.1节所述。这样的轮廓曲线还可以与常规图像边缘结合,构建完整的
表面模型(Y cer,Kim等人,2016),如Figure12.26c所示。
12.8 单眼深度估计
从单张图像推断(或幻觉?)深度图的能力开启了各种创意可能性,例如以三维形式展示(图6.41和Kopf、Matzen等人2020年),创造柔焦效果(Section10.3.2),以及可能辅助场景理解。它还可以用于机器人应用,如自主导航(图12.31),尽管大多数(自主和常规)车辆配备了计算机视觉系统后,通常会安装多个摄像头或测距传感器。
我们在第6.4.4节中已经看到,自动照片弹出系统如何利用图像分割和分类来创建照片的“纸板剪影”版本(Hoiem、Efros和Hebert 2005a;Saxena、Sun和Ng 2009)。更近期的系统通过单张图像推断深度时使用了深度神经网络。这些内容在两篇最近的综述文章中有详细描述(Poggi、Tosi等2021,第7节;Zhao、Sun等2020),讨论了超过20种和50多种方法。

图12.31来自KITTI数据集(Godard、Mac Aodha和Brostow2017)的单目深度图估计值©2017 IEEE。
分别使用相关技术,并在Figure12.31中所示的KITTI数据集(Geiger、Lenz和Urtasun2012)上对其进行基准测试。
最早使用神经网络计算深度图的论文之一是Eigen、Pursh和Fergus(2014)开发的系统,该系统随后被扩展以推断表面法线和语义标签(Eigen和Fergus 2015)。这些系统在纽约大学深度数据集V2 (Silberman、Hoiem等2012)和KITTI数据集上进行了训练和测试,如图12.30所示。此后,大多数相关研究都在这两个相对受限的数据集(室内公寓或室外街道场景)上进行训练和测试,尽管有时作者也会使用Make3D (Saxena、Sun和Ng 2009)或Cityscapes (Cordts、Omran等2016),这两个都是室外街道场景,或者ScanNet (Dai、Chang等2017),它包含室内场景。在这样的“封闭世界”数据集上训练和测试的危险在于,网络可能会学习捷径,例如根据地面位置推断深度,或者未能识别出不属于常见类别的物体(van Dijk和de Croon 2019)。
早期系统使用了诸如NYU depth、KITTI和ScanNet等数据集中的深度图像进行训练,事实证明,在这些数据集中加入共面性等软约束可以提高性能(Wang,Shen等人,2016;Yin,Liu等人,2019)。后来,引入了“无监督”技术,利用变形立体图像对之间的光度一致性(Godard,Mac Aodha,和Brostow,2017;Xian,Shen等人,2018)或视频序列中图像对的光度一致性(Zhou,Brown等人,2017)。此外,还可以使用著名地标3D重建(Li和Snavely,2018),包含人们摆出“人体挑战”姿势的图像集(Li,Dekel等人,2019),或者采集更多样化的“野外图像”,并标注相对深度(Chen,Fu等人,2016)。
最近一篇将多个此类数据集联合起来的论文是Ranftl、Lasinger等人(2020)开发的MiDaS系统,他们不仅使用了大量现有的“野外”数据集来训练基于Xian、Shen等人(2018)提出的网络,还利用了来自十几部3D电影的数千对立体图像作为额外的训练、验证和测试数据。在他们的论文中,他们不仅展示了该系统比先前的方法产生了更优的结果。

图12.32COCO数据集(Ranftl,Lasinger等人,2020)中的单目深度地图估计和图像的新视图©2020 IEEE。
(图12.32),但同时也认为他们的零样本跨数据集转移协议,即在与训练集分开的数据集上进行测试,而不是使用随机的训练和测试子集,产生了一个在真实世界图像上工作更好的系统,并避免了意外的数据集偏差(Torralba和Efros2011)。
从单张图像推断深度图的另一种方法是推断完整的封闭3D形状,可以使用体素表示(Choy,Xu等2016;Girdhar,Fouhey等2016;Tulsiani,Gupta等2018)或基于网格的表示(Gkioxari,Malik和Johnson 2019;Han,Laga和Bennamoun 2021)。除了将深度网络应用于单张彩色图像外,还可以通过添加额外的线索和表示来增强这些网络,例如定向线和平面(Wang,Geraghty等2020),这些作为高层次的形状先验(第12.7.2节和第13.6.1节)。神经渲染也可用于创建新颖视角(Tucker和Snavely 2020;Wiles,Gkioxari等2020;图14.22d),并使单目深度预测随时间保持一致(Luo,Huang等2020;Teed和Deng 2020a;Kopf,Rong和Huang 2021)。单目深度推断的一个消费级应用示例是一次性3D摄影(Kopf,Matzen等2020),该系统使用紧凑高效的DNN在手机上实现,首先推断出深度图,然后将其转换为多层,修复背景,创建网格和纹理图集,
12.9 额外阅读
立体对应和深度估计领域是计算机视觉中最古老且研究最为广泛的主题之一。多年来,许多优秀的综述文章已经问世(Marr和Poggio 1976;Barnard和Fischler 1982;Dhond和Aggarwal 1989;Scharstein和Szeliski 2002;Brown、Burschka和Hager 2003;Seitz、Curless等2006;Furukawa
以及Hern ndez2015
;Janai,G ney等人2020;Laga,Jospin等人2020;Poggi,Tosi等人。
(2021),它们可以作为这大量文献的良好指南。
由于计算限制和寻找外观不变对应关系的需要,早期算法通常专注于寻找稀疏对应关系(Hannah 1974;Marr和Poggio 1979;Mayhew和Frisby 1980;Ohta和Kanade 1985;Bolles、Baker和Marimont 1987;Matthies、Kanade和Szeliski 1989)。
计算极线几何和预校正图像的主题在第11.3节和第12.1节中有所涉及,同时也在多视图几何的教科书中(Faugeras和Luong 2001;Hartley和Zisserman 2004)以及专门讨论这一主题的文章中(Torr和Murray 1997;Zhang 1998a,b)有所涉及。视差空间和视差空间图像的概念通常与Marr(1982)的开创性工作以及Yang、Yuille和Lu(1993)和Intille和Bobick(1994)的论文联系在一起。平面扫描算法最初由Collins(1996)推广,随后由Szeliski和Golland(1999)将其扩展到完整的任意射影设置,Saito和Kanade(1999)也进行了类似的推广。平面扫描还可以使用圆柱面(Ishiguro、Yamamoto和Tsuji 1992;Kang和Szeliski 1997;Shum和Szeliski 1999;Li、Shum等2004;Zheng、Kang等2007)或更一般的拓扑结构(Seitz 2001)来表述。
一旦成本体积或DSI的拓扑结构已经建立,我们需要计算每个像素和潜在深度的实际照片一致性度量。如第12.3.1节所述,已提出了多种此类度量方法。其中一些在下文中进行了比较。
最近对匹配成本的调查和评估(Scharstein和Szeliski2002;Hirschm ller
和Scharstein2009)。
为了从这些成本计算出实际的深度图,必须使用某种形式的优化或选择标准。最简单的方法是各种类型的滑动窗口,相关内容在第12.4节中讨论,并由Gong、Yang等人(2007)和Tombari、Mattoccia等人(2008)进行了综述。全局优化框架常用于计算最佳视差场,如第12.5节所述。这些技术包括动态规划和真正的全局优化算法,例如图割和循环信念传播。最近,深度神经网络在计算对应关系和视差图方面变得流行,相关内容在第12.6节中讨论,并由Laga、Jospin等人(2020)进行了综述。
Poggi、Tosi等人(2021年)。表12.1中的基准列表是查找该领域最新结果的绝佳途径。
多视图立体算法通常分为两类(Furukawa和Hern ndez 2015)。第一类包括使用多张图像计算
传统深度图的算法,以计算照片一致性度量(Okutomi和Kanade 1993;Kang、Webb等1995;Szeliski和Golland 1999;Vaish、Szeliski等2006;Gallup、Frahm等2008;Huang、Matzen等2018;Yao、Luo等2018)。其中一些技术计算多个深度图,并使用额外的约束条件来鼓励不同的深度图相互匹配。
一致(Szeliski1999a;Kolmogorov和Zabih2002;Kang和Szeliski2004;Maitre、Shinagawa和Do2008;Zhang、Jia等人2008;Yan、Wei等人2020;Zhang、Yao等人2020)。
第二类论文是计算真实的三维体积或基于表面的对象模型。同样,由于关于这个主题发表的论文数量庞大,我们在这里不引用它们,而是将您引向第12.7.2节中的材料,Seitz的调查,
Curless等人(2006)、Furukawa和Hern ndez(2015
)以及Janai、G ney等人(2020)
表12.1中列出的在线评价网站。
单目深度推断这一主题目前非常活跃。除了第12.8节之外,Poggi、Tosi等人(2021,第7节)和Zhao、Sun等人(2020)的最新综述也是很好的起点。
12.10 练习
例12.1:立体声对校正。实现以下简单算法(Section12.1.1):
1.旋转两个摄像机,使它们与连接两个摄像机中心c0和c1的直线垂直。最小旋转可以从原始和期望的光轴之间的交叉积计算得出。
2.旋转光轴,使每个摄像机的水平轴朝向另一个摄像机的方向。(同样,第一次旋转后当前x轴与连接摄像机的线之间的叉积给出了旋转。)
3.如果需要,放大较小(细节较少)的图像,使其具有与其他图像相同的分辨率(因此具有行与行对应关系)。
现在将您的结果与Loop和Zhang(1999)提出的算法进行比较。您是否可以想到在哪些情况下他们的方法可能更可取?
Chapter 13 3D reconstruction
13.1从X中获得形状 809
13.1.1从阴影和光度立体法生成形状 809
13.1.2从纹理中提取形状 814
13.1.3从焦点中提取形状 814
13.2三维扫描 816
13.2.1范围数据合并 820
13.2.2应用:数字遗产 824
13.3表面表示 825
13.3.1表面插值 826
13.3.2表面简化 827
13.3.3几何图像 828
13.4基于点的表示 829
13.5容量表示 830
13.5.1隐式曲面和水平集 831
13.6基于模型的重建 833
13.6.1建筑 833
13.6.2面部建模和跟踪 838
13.6.3应用:面部动画 839
13.6.4人体建模和跟踪 843
13.7恢复纹理贴图和反照率 850
13.7.1估算BRDF 852
13.7.2应用:3D模型捕捉 854
13.8额外阅读材料 855

图13.1三维形状获取和建模技术:(a)阴影图像(Zhang,
Tsai等人,1999)©1999 IEEE;(b)纹理梯度(G rding1992)©1992 Springer;(c)
实时深度从焦点(Nayar、Watanabe和Noguchi 1996)©1996 IEEE;用棍子阴影扫描场景(Bouguet和Perona 1999)©1999斯普林格;(e)将范围图合并成三维模型(Curless和Levoy 1996)©1996 ACM;(f)基于点的表面建模(Pauly、Keiser等2003)©2003 ACM;(g)使用线和平面自动建模三维建筑(Werner和Zisserman 2002)©2002斯普林格;(h)时空立体中的三维面部模型(Zhang、Snavely等2004)©2004 ACM;(i)从单张图像中拟合全身、表情和手势(Pavlakos、Choutas等2019)©2019 IEEE。
正如我们在前一章所见,已经开发了许多立体匹配技术,用于从两张或多张图像中重建高质量的3D模型。然而,立体只是众多可用于从图像推断形状的线索之一。在本章中,我们将探讨多种此类技术,不仅包括诸如阴影和焦点等视觉线索,还包括将多个范围或深度图像合并成3D模型的技术,以及重建特定模型的技术,如头部、身体或建筑。
在用于推断形状的各种线索中,表面的阴影(图13.1a)可以提供大量关于局部表面方向的信息,从而揭示整体表面形状(第13.1.1节)。当不同方向的灯光可以分别开启和关闭时,这种方法变得更加强大(光度立体)。纹理梯度(图13.1b),即随着表面倾斜或远离相机弯曲而形成的规则图案的缩短,也能提供类似的局部表面方向线索(第13.1.2节)。焦点是另一种强大的场景深度线索,尤其是在使用两个或多个具有不同焦距设置的图像时(第13.1.3节)。
三维形状也可以通过主动照明技术估算,例如光条纹(图13.1d)或飞行时间测距仪(第13.2节)。使用这些技术(或基于图像的立体)获得的部分表面模型可以合并成更连贯的三维表面模型(图13.1e),如第13.2.1节所述。这些技术已被用于构建高度详细且精确的文化遗产模型,如历史遗址(第13.2.2节)。生成的表面模型随后可以简化,以支持不同分辨率的查看和网络流传输(第13.3.2节)。除了处理连续表面外,还可以将三维表面表示为密集的三维定向点集合(第13.4节)或体积元素(第13.5节)。
3D建模如果了解我们试图重建的对象,可以更加高效和有效。在第13.6节中,我们将探讨三个专门但常见的例子,即建筑(图13.1g)、头部和面部(图13.1h)以及全身(图13.1i)。除了建模人物外,我们还将讨论跟踪他们的技术。
形状和外观建模的最后阶段是提取一些彩色纹理,用于绘制到我们的3D模型上(第13.7节)。有些技术甚至超越了这一点,实际上估计完整的BRDF(第13.7.1节),尽管如果不想重新照亮场景,获取表面光场可能更容易(第14.3.2节)。
由于存在如此多样的技术来执行三维建模,本章不详细讨论其中任何一种。鼓励读者在引用的参考文献和最近的计算机视觉会议上找到更多信息,以及更多
专门讨论这些主题的会议,例如,国际三维视觉会议(3DV)和IEEE国际自动面部和手势识别会议(FG)。
13.1 从X中获得形状
除了双眼视差外,阴影、纹理和焦点都在我们感知形状的过程中起着作用。从这些线索推断出形状的研究有时被称为“从X中提取形状”,因为各个实例分别称为从阴影中提取形状、从纹理中提取形状和从焦点中提取形状。1在本节中,我们将探讨这三种线索及其如何用于重建三维几何。关于所有这些主题的良好概述可以在Wolff、Shafer和Healey(1992b)编辑的基于物理的形状推断论文集、Ackermann和Goesele(2015)的综述以及Ikeuchi、Matsushita等人(2020)的书中找到。
当你看到平滑着色物体的图像时,比如图13.2中所示的那些,仅凭阴影的变化就能清楚地看出物体的形状。这怎么可能呢?答案是,随着物体表面法线的变化,物体的表观亮度会根据局部表面方向与入射光照之间的角度变化而变化,如图2.15(第2.2.2节)所示。
从这种强度变化中恢复表面形状的问题被称为阴影中的形状,是计算机视觉中的经典问题之一(Horn 1975)。霍恩和布鲁克斯(1989)编辑的论文集是这一主题的重要资料来源,特别是关于变分方法的那一章。张、蔡等人(1999)的综述不仅回顾了更近期的技术,还提供了一些比较结果。
大多数基于阴影算法的形状假设认为所考虑的表面具有均匀的反照率和反射率,并且光源方向要么已知,要么可以通过使用参考物体进行校准。在远距离光源和观察者假设下,强度变化(辐照度方程)完全取决于局部表面的方向,
I(x,
y) = R(p(x, y), q(x, y)), (13.1)
1我们在第12章已经看到了立体形状、轮廓形状和剪影形状的例子。

图13.2从阴影中合成形状(Zhang,Tsai等人,1999)©1999 IEEE:阴影图像,(a-b)光线来自前方(0,0,1),(c-d)光线来自右前方(1,0,1);(e-f)使用Tsai和Shah(1994)的技术从阴影重建得到的相应形状。
其中(p,q)=(zx,zy)是深度图的导数,R(p,q)称为反射率图。例如,漫射(朗伯)表面的反射率图是(非
表面法线=(p,q,1)/√1+p2+q2与的点积(2.89)为负
=
max
(13.2)
其中P为表面反射率因子(反照率)。
原则上,方程(13.1-13.2)可以用来估计(p,q),使用非线性最小二乘法或其他方法。不幸的是,除非施加额外的约束条件,否则每个像素(p,q)的未知数比测量值(I)多。一个常用的约束条件是平滑度约束,
我们在第4.2节(4.18)中已经看到过。另一个是可积性约束,εi =∫(py—qx)2 dx dy, (13.4)
这是自然产生的,因为对于一个有效的深度图z(x,y),(p,q)=(zx,zy),我们有py = zxy = zyx = qx。
与其首先恢复方向场(p,q),并将其积分以获得表面,也可以直接最小化图像形成方程(13.1)中的差异,同时找到最优深度图z(x,y)(Horn 1990)。不幸的是,从阴影中提取形状容易受到搜索空间中的局部最小值的影响,与其他涉及多个变量的同时估计的变分问题一样,也可能存在收敛缓慢的问题。使用多分辨率技术(Szeliski 1991a)可以帮助加速收敛,而使用更复杂的优化技术(Dupuis和Olienis 1994)则可以帮助避免局部最小值。
在实际应用中,除了石膏模型外,其他表面很少具有单一均匀的反照率。因此,从阴影中提取形状的方法需要与其他技术结合或以某种方式扩展,才能发挥作用。一种方法是将其与立体匹配(Fua和Leclerc 1995;Logothetis、Mecca和Cipolla 2019)或已知纹理(表面图案)相结合(White和Forsyth 2006)。立体匹配和纹理成分在有纹理的区域提供信息,而从阴影中提取形状则有助于填补均匀颜色区域的信息,并提供更精细的表面形状信息。
光度立体法。另一种使阴影形状更可靠的方法是使用多个光源,这些光源可以有选择地开启和关闭。这种技术被称为光度立体法,因为光源的作用类似于传统立体中位于不同位置的相机(Woodham 1981)。对于每个光源,我们都有一个不同的反射率图,R1(p,q),R2(p,q)等。给定像素处的相应强度I1、I2等,原则上我们可以恢复未知的反照率P和表面方向估计(p,q)。
对于漫射表面(13.2),如果用参数化局部方向,我们得到(对于非阴影像素)一组线性方程,形式如下
Ik = P · vk , (13.5)
我们可以通过线性最小二乘法从这些方程中恢复出P。只要(三个或更多)向量vk是线性独立的,即它们不在同一方位角(远离观察者的方向),这些方程就是条件良好的。
2关灯的替代方法是使用三种颜色的灯光(Woodham1994;Hernandez、Vogiatzis等人2007;Hernandez和Vogiatzis2010)。

图13.3多视图光度立体(Logothetis、Mecca和Cipolla2019)©2019 IEEE:初始COLMAP多视图立体重建;经过(Park、Sinha等人2017)和(Logothetis、Mecca和Cipolla2019)的细化。
一旦每个像素的表面法线或梯度被恢复,就可以使用正则化表面拟合的变体(4.24)将其整合到深度图中。Nehab、Rusinkiewicz等人(2005)和Harker、O‘Leary(2008)讨论了更复杂的技术来实现这一点。多视图立体用于粗略形状,光度立体用于精细细节的结合仍然是一个活跃的研究领域(Hern ndez、Vogiatzis和Cipolla 2008;Wu、Liu等人2010;Park、Sinha等人2017)。Logothetis、Mecca和Cipolla
(2019)描述了一种可以生成非常高质量扫描的系统(图13.3),尽管它需要复杂的实验室设置。Cao、Waechter等人(2020)描述了一种更为实用的设置,仅需一台立体相机和一个闪光灯即可生成闪光/非闪光对。此外,还可以将光度立体应用于户外网络摄像头序列(图13.4),利用太阳的轨迹作为可变方向照明器(Ackermann、Langguth等人2012)。
当表面是镜面时,可能需要超过三个光照方向。事实上,公式(13.1)给出的辐射方程不仅要求光源和相机远离表面,还忽略了相互反射,这可能是物体表面阴影的重要来源,例如,在凹陷结构如沟槽和裂缝内部观察到的变暗现象(Nayar,Ikeuchi,和Kanade 1991)。然而,如果能够控制光源和相机的位置,使其互为镜像,即可以(概念上)交换光源和相机的位置,则可以通过一种称为赫尔姆霍兹立体视觉的方法来恢复表面深度和法线的约束条件(Zickler,Belhumeur,和Kriegman 2002)。
早期的光度立体研究假定已知照明方向和反射率(BRDF)函数,而最近的研究则旨在放宽这些限制。

图13.4基于网络摄像头的室外光度立体(Ackermann,Langguth等人,2012年)©2012 IEEE:输入图像、恢复的法线图、三个基础BRDF,它们分别位于各自的材质图之下,以及从新的太阳位置合成的渲染。

图13.5从纹理合成形状(G rding1992)©1992 Springer: (a) regular
纹理包裹在曲面上,以及相应的表面法线估计。形状从镜面反射(Savarese、Chen和Perona 2005)©2005斯普林格出版社:(c)规则的图案反射在曲面镜上会产生(d)曲线,从中可以推断出三维点的位置和法线。
戈塞勒(2015)对这些技术进行了广泛的综述,而石、莫等人(2019)则描述了他们的DiLiGenT数据集和评估非朗伯光度立体的基准,并引用了超过100篇相关论文。与其他计算机视觉领域一样,深度网络和端到端学习现在常用于从光度立体中恢复形状和光照方向。一些最近的论文包括陈、韩等人(2019)、李、罗布尔斯-凯利等人(2019)、海夫纳、叶等人(2019)、陈、瓦赫特等人(2020)以及桑托、瓦赫特和松下(2020)。
在规则纹理中观察到的缩短变化也可以提供有关局部表面方向的有用信息。图13.5展示了一个这样的模式示例,以及估计的局部表面方向。从纹理形状算法需要多个处理步骤,包括提取重复图案或测量局部频率以计算局部仿射变形,以及后续阶段推断局部表面方向。这些不同阶段的详细信息可以在研究文献中找到(Witkin 1981;Ikeuchi 1981;Blostein和Ahuja 1987;G rding 1992;Malik和Rosenholtz 1997;Lobay和Forsyth 2006)。一篇更近期的论文使用生成模型来表示纹理的重复出现,并在每个像素处联合优化模型与局部
表面方向(Verbin和Zickler 2020)。
当原始图案规则时,可以将一个规则但略有变形的网格拟合到图像上,并使用该网格进行各种图像替换或分析任务(Liu,Collins和Tsin 2004;Liu,Lin和Hays 2004;Hays,Leordeanu等2006;Lin,Hays等2006;Park,Brocklehurst等2009)。如果使用特别打印的纹理布料图案,这一过程会变得更加容易(White和Forsyth 2006;White,Crane和Forsyth 2007)。
如图13.5c-d所示,当物体在弯曲镜面的反射中以规则模式变形时,可以利用这些变形恢复表面形状(Savarese、Chen和Perona 2005;Rozenfeld、Shimshoni和Lindenbaum 2011)。此外,还可以从镜面流中推断局部形状信息,即从移动摄像机视角观察镜面运动时的信息(Oren和Nayar 1997;Zisserman、Giblin和Blake 1989;Swaminathan、Kang等人2002)。
物体深度的一个强烈线索是模糊的程度,随着物体表面远离相机的对焦距离而增加。如图2.19所示,当物体表面远离对焦平面时,根据相似三角形(练习2.4)容易建立的公式,混淆圈会增大。
已经开发出多种技术,用于从模糊程度估计深度(由模糊产生的深度)(Pentland1987;Nayar和Nakagawa1994;Nayar、Watanabe和Noguchi1996;Watanabe和Nayar1998;Chaudhuri和Rajagopalan1999;Favaro和Soatto2006)。为了使这种技术实用,需要解决一些问题:
•从对焦平面移开时,两个方向上的模糊程度都会增加。因此,有必要使用不同对焦拍摄的两张或更多张图像

图13.6实时失焦深度(Nayar,Watanabe和Noguchi 1996)©1996 IEEE:(a)实时焦点范围传感器,包括两个远心透镜之间的半镀银镜(右下),一个将图像分成两个CCD传感器的棱镜(左下),以及由氙灯照亮的锯齿形棋盘图案(顶部);(b–c)来自两个摄像头的输入视频帧及其对应的深度图;(e–f)两帧图像(放大后可以看到纹理)和(g)对应的3D网格模型。
距离设置(Pentland1987;Nayar、Watanabe和Noguchi1996)或在深度上转换物体并寻找最大锐度点(Nayar和Nakagawa 1994)。
•物体的放大倍率会随着焦距距离的变化或物体的移动而变化。这可以通过显式建模(使对应关系更加复杂)或使用远心光学来实现,后者近似于正射相机,并且需要在镜头前设置光阑(Nayar,Watanabe,和Noguchi 1996)。
必须可靠地估计失焦量。一种简单的方法是计算一个区域的平方梯度的平均值,但这种方法存在一些问题,包括上面提到的图像放大问题。更好的解决方法是使用精心设计的有理滤波器(Watanabe和Nayar1998)。
图13.6展示了一个实时深度数据的示例,该系统使用了两个位于不同深度但共享同一光路的成像芯片,以及一个从同一方向投射棋盘图案的主动照明系统。如图13.6b至g所示,该系统能够为静态和动态场景生成高精度的实时深度图。

图13.7范围数据扫描(Curless和Levoy 1996)©1996 ACM:(a)表面上的激光点由CCD传感器成像;(b)激光条带(片)由传感器成像(条带的变形编码了到物体的距离);(c)成果的3D点集被转换为(d)三角网格。
13.2 三维扫描
正如我们在前一节中所见,主动照明场景,无论是为了使用光度立体法估计法线,还是为了通过离焦生成形状的人工纹理,都能显著提升视觉系统的性能。这种主动照明技术自机器视觉早期就已用于构建高精度传感器,以利用各种测距(或测距感应)技术估算三维深度图像(Besl1989;Curless1999;Hebert2000;Zhang2018)。虽然像激光雷达(光检测和测距)和基于激光的3D扫描仪这样的测距设备曾经仅限于商业和实验室应用,但低成本深度相机如微软Kinect(Zhang2012)的发展彻底改变了计算机视觉的许多方面。现在,通常将此类相机生成的注册彩色和深度帧称为RGB-D(或RGBD)图像(Silberman,Hoiem等2012)。
早期用于计算机视觉和计算机图形学的主动照明传感器之一是激光或光条传感器,它从偏移视角观察场景或物体时,在光面上扫过,如图13.7b所示(Rioux和Bird 1993;Curless和Levoy 1995)。当光条落在物体上时,它会根据所照亮表面的形状改变其形状。然后,利用光学三角测量法可以简单地估计出特定光条中所有可见点的三维位置。更详细地说,通过了解光条的三维平面方程,我们可以推断出每个被照亮像素对应的三维位置,正如之前讨论的(2.70–2.71)。通过找到精确的时间峰值,可以提高光条技术的准确性。

图13.8使用投射阴影进行形状扫描(Bouguet和Perona 1999)©1999斯普林格:相机设置包括一个点光源(台灯但没有反光罩)、一根手持棍子投射阴影,以及(b)被扫描物体位于两个平面背景前。(c)使用脉冲照明系统实时生成深度图(Iddan和Yahav 2001)©2001 SPIE.
每个像素的照明(Curless和Levoy,1995)。扫描仪的最终精度可以通过斜边调制技术来确定,即通过成像校准对象中的锐利折痕(Goesele、Fuchs和Seidel,2003)。
布盖和佩罗纳(1999)提出了一种有趣的光条测距变体。他们没有投射光条,而是简单地挥动一根棍子,在由点光源如灯或太阳照亮的场景或物体上投下阴影(图13.8a)。由于两个背景平面相对于相机的方向已知(或在预校准过程中推断),每个条纹的平面方程可以从两条投影线中推导出来,这两条线的三维方程是已知的(图13.8b)。当阴影穿过被扫描物体时,其变形揭示了该物体的三维形状,就像常规光条测距一样(练习13.2)。这种技术还可以用于估计背景场景的三维几何形状及其在进入阴影时外观的变化,从而在场景中投射新的阴影(Chuang,Goldman等人,2003)(Section10.4.3)。
使用光条纹技术扫描物体所需的时间与所使用的深度平面数量成正比,这通常与图像中的像素数量相当。通过以结构化的方式开启和关闭不同的投影像素,可以构建一个更快的扫描仪,例如使用二进制或灰度码(Besl1989)。例如,假设我们使用的LCD投影仪有1,024列像素。取每列地址对应的10位二进制代码(0...1,023),我们依次投射第一位、第二位等。经过10次投射(例如,在同步30Hz的摄像机-投影仪系统中为三分之一秒),相机中的每个像素都知道它看到的是投影仪光的哪一列中的哪个像素。类似的方法也可以用于估计折射率。

图13.9微软Kinect深度相机(张2012)©2012 IEEE:(a)硬件,包括红外(IR)斑点图案投影仪和彩色及红外摄像头组合;(b)样本红外图像的特写,显示了投射的点;(c)最终深度图,在未被投影仪照亮的区域有黑色“阴影”。
通过在物体后面放置一个监视器来检测物体的特性(Zongker,Werner等人,1999;Chuang,Zongker等人,2000)(第14.4节)。也可以用单个激光束构建非常快速的扫描仪,即实时飞点光学三角测量扫描仪(Rioux,Bechthold等人,1987)。
如果需要更快,即帧率更高的扫描,我们可以将单一纹理图案投射到场景中。Proesmans、Van Gool和Defoort(1998)描述了一种系统,该系统将棋盘网格投影到物体上,并利用网格的变形来推断三维形状。不幸的是,这种技术只有在表面足够连续以连接所有网格点时才有效。除了投影网格外,还可以投影一个或多个正弦条纹图案,然后通过相对相位位移恢复表面的变形,这一过程称为条纹投影轮廓测量法(Su和Zhang 2010;Zuo、Huang等2016;Zhang 2018)。
微软Kinect(张2012)深度相机采用了一种类似的技术,投射出一个红外(IR)斑点图案,看起来像是一堆随机的点,但实际上是由已知校准的伪随机模式组成(图13.9)。通过测量红外相机中看到的点与其预期位置之间的水平位移(视差),可以计算出深度图,在未被点照亮的像素上进行插值(法内洛,雷曼等2016;法内洛,瓦伦丁等2017b)。自发布以来,Kinect相机在计算机视觉研究中得到了广泛应用(张2012;韩,邵等2013),以及诸如3D人体跟踪(Section13.6.4)和物体扫描及家庭内部重建等应用(第13.2.1节)。Kinect传感器被用于创建首个广泛使用的3D语义场景理解数据集(西尔伯曼,霍伊姆等2012),尽管后来也创建了更大的3D扫描数据集(戴,张等2017)。 可以使用高速定制照明和传感硬件构建更高分辨率的系统。Iddan和Yahav(2001)描述了他们3DV Zcam的构建

图13.10使用时空立体技术实时密集3D面部捕捉(张、斯纳维利等,2004)©2004 ACM:来自两个立体相机之一的五帧连续视频(每第五帧不含条纹图案,以便提取纹理);(b)生成的高质量3D表面模型(深度图以着色渲染的形式展示)。
视频速率深度感知相机,它将脉冲光平面投射到场景中,然后在短时间内积分返回的光线,从而获得场景中各个像素距离的时间飞行测量。关于早期时间飞行系统的详细描述,包括激光雷达的幅度和频率调制方案,可参见(Besl1989),而更近期的描述则可以在Hansard、Lee等人(2012)的书中找到。虽然微软Kinect深度相机的最初版本使用了斑点图案结构光系统(Zhang2012),但更新的Kinect V2采用了一种时间飞行(ToF)传感器,该传感器利用幅度调制光信号的相位测量(Bamji,O‘Connor等,2014)。传统的多频相位解缠技术可用于估计绝对深度,但对于动态场景,通过同时建模深度和物体速度可以获得更精确的深度(St hmer,Nowozin等,2015)。
与其使用单个摄像头,也可以通过立体成像装置构建主动照明范围传感器,从而形成通常被称为主动(照明)立体的系统。最简单的方法是向场景投射随机条纹图案以创建合成纹理,这有助于匹配无纹理表面(康、韦伯等人,1995)。就像编码图案单摄像头测距一样,投射已知的一系列条纹可以使像素之间的对应关系明确,并允许仅在单个摄像头中看到的像素恢复深度估计(沙尔斯坦和舍利斯基,2003)。该技术已被用于生成大量高度准确的多图像立体对和深度图,以评估立体对应算法(沙尔斯坦和舍利斯基,2002;希施勒和沙尔斯坦,2009;沙尔斯坦、希施勒等人,2014),并学习深度图先验和参数(帕尔、温曼等人,2012)。精心设计的算法可以在500赫兹下执行局部模式匹配(法内洛、瓦伦丁。等,2017a、b)。
虽然投影多个图案通常需要场景或物体保持静止,但额外的处理可以为动态场景生成实时深度图。基本思路(Davis,Ramamoorthi和Rusinkiewicz 2003;Zhang,Curless和Seitz 2003)是假设每个像素周围的三维时空窗口内的深度几乎恒定,并使用该三维窗口进行匹配和重建。根据表面形状和运动的不同,这一假设可能会出错,如Davis,Nahab等人(2005)所示。为了更准确地建模形状,Zhang,Curless和Seitz(2003)在时空窗口内建模线性视差变化,并表明通过全局优化视频体积中的视差和视差梯度估计可以获得更好的结果(Zhang,Snavely等人2004)。图13.10显示了将此系统应用于人脸的结果;帧率3D表面模型随后可用于进一步的基于模型的拟合和计算机图形操作(Section13.6.2)。如前所述,运动建模
也可应用于基于相位的飞行时间传感器(St hmer,Nowozin等人,2015)。
关于主动测距的一个注意事项。当被扫描表面过于反光时,相机可能会看到物体表面的反射,并认为这个虚拟图像就是真实场景。对于中等程度反光的表面,如Wood等人(2000)中的陶瓷模型或Park、Newcombe和Seitz(2018)中的玉米卷,即使在镜面层下仍有足够的漫反射,仍可获得三维测距图。(然后可以单独恢复镜面部分,以生成表面光场,具体方法见第14.3.2节。)然而,对于真正的镜子,主动测距仪不可避免地会捕捉到镜中反射的虚拟三维模型,因此必须使用其他技术,例如寻找扫描设备的反射(Whelan、Goesele等人,2018)。
虽然单个范围图像对于实时Z键或面部运动捕捉等应用非常有用,但它们通常被用作更完整3D物体建模的构建模块。在这些应用中,接下来的两个处理步骤是部分3D表面模型的配准(对齐)及其整合到连贯的3D表面上(Curless 1999)。如果需要,可以随后进行模型拟合阶段,使用参数化表示如广义圆柱体(Agin和Binford 1976;Nevatia和Binford 1977;Marr和Nishihara 1978;Brooks 1981)、超二次曲面(Pentland 1986;Solina和Bajcsy 1990;Terzopoulos和Metaxas 1991),或非参数模型如三角网格(Boissonat 1984)或基于物理的模型(Terzopoulos、Witkin和Kass 1988;Delingette、Hebert和Ikeuichi 1992;Terzopoulos和Metaxas 1991;McInerney和Terzopoulos 1993;Terzopoulos 1999)。还开发了多种用于分割范围的技术。
将图像转换为更简单的构成表面(Hoover,Jean-Baptiste等人,1996)。
最常用的三维配准技术是迭代最近点(ICP)算法,该算法在寻找两个待对齐表面之间的最近点匹配和解决三维绝对定向问题之间交替进行(第8.1.5节,(8.31-8.32)(Besl和McKay 1992;Chen和Medioni 1992;Zhang 1994;Szeliski和Lavall e 1996;Gold、Rangarajan等人1998;David、DeMenthon等人2004;Li和Hartley
2007;Enqvist、Josephson和Kahl 2009)。一些技术,如Chen和Medioni(1992)开发的技术,使用局部表面切平面来提高计算精度并加速收敛。最近,Rusinkiewicz(2019)提出了一种类似于定向粒子中使用的能量项的对称定向点距离(Szeliski和Tonnesen 1992)。Tam、Cheng等人(2012)和Pomerleau、Colas和Siegwart(2015)的论文对ICP及其相关变体进行了很好的综述。
由于两个表面通常只有部分重叠且可能存在异常值,因此通常使用鲁棒匹配标准(第8.1.4节和附录B.3)。为了加快最近点的确定速度,并使距离计算更加精确,可以将两个点集之一(例如当前合并模型)转换为带符号的距离函数,可选择使用八叉树样条表示以提高紧凑性(Lavall e和Szeliski 1995)。基本ICP算法的变体可用于在非刚性变形下注册3D点集,例如在医学应用中(Feldmar和Ayache 1996;Szeliski
和Lavall e 1996)。与点或范围测量相关的颜色值也可以作为注册过程的一部分来提高鲁棒性(Johnson和Kang 1997;Pulli 1999)。
不幸的是,ICP算法及其变体只能找到三维表面之间的局部最优对齐。如果事先不知道这一点,则需要使用基于局部描述符的更全局的对应或搜索技术,这些描述符对三维刚性变换具有不变性。例如,自旋图像是一种围绕局部法线轴的三维表面区域的局部圆形投影(Johnson和Hebert 1999)。另一个(较早的)例子是Stein和Medioni(1992)引入的溅射表示。近年来,相关研究探讨了从RGB-D图像中估计姿态的问题(第11.2节),这实际上与将范围图对齐到3D模型相同。最近关于这一主题的论文(Drost,Ulrich等人2010;Brachmann,Michel等人2016;Vidal,Lin等人2018)通常会在6DOF物体姿态估计基准测试上进行评估,该基准测试还每年举办一系列关于此主题的工作坊。
在对两个或多个三维表面进行对齐之后,可以将它们合并成一个模型。一种方法是使用三角化网格表示每个表面并组合这些

图13.11范围数据合并(Curless和Levoy 1996)©1996 ACM:(a)两个带符号的距离函数(左上)与其(权重)在左下合并,生成一组组合函数(右列),从中可以提取等值面(绿色虚线);(b)带符号的距离函数与空和未见空间标签结合,以填补等值面上的孔洞。
使用一种有时称为“拉链”(Soucy和Laurendeau 1992;Turk和Levoy 1994)的过程来构建网格。另一种现在更为广泛采用的方法是计算一个(截断的)带符号距离函数,该函数拟合所有三维数据点(Hoppe、DeRose等1992;Curless和Levoy 1996;Hilton、Stoddart等1996;Wheeler、Sato和Ikeuchi 1998)。
图13.11展示了一种方法,即由Curless和Levoy(1996)开发的体积范围图像处理(VRIP)技术。该技术首先从每个范围图像计算出加权有符号距离函数,然后通过加权平均过程将它们合并。为了使表示更加紧凑,使用了游程编码来编码空、可见和变化(有符号距离)体素,仅存储每个表面附近的有符号距离值。一旦计算出合并后的有符号距离函数,就可以使用零交叉表面提取算法,如行进立方体(Lorensen和Cline 1987),来恢复网格化的表面模型。图13.12展示了完整的范围数据合并和等值面提取流程的一个例子。Rusinkiewicz、Hall-Holt和Levoy(2002)提出了一种实时系统,结合了快速ICP和基于点的合并与渲染。
消费级RGB-D相机如Kinect的出现,重新激发了人们对大规模范围数据注册和合并的兴趣(Zhang2012;Han,Shao et al.2013)。该领域的一篇有影响力的文章是Kinect Fusion (Izadi,Kim et al.2011;Newcombe,Izadi et al.
5一种替代的、更紧凑的表示方法是使用八叉树(Lavall e和Szeliski 1995)。

图13.12“快乐佛”雕像的重建和硬拷贝(Curless和Levoy1996)©1996 ACM:喷漆后的原始雕像照片
哑光灰色;(b)部分范围扫描;(c)合并范围扫描;(d)重建模型的彩色渲染;(e)使用立体光刻构建的模型的硬拷贝。

图13.13使用KinectFusion实时系统融合多个深度图像(New- combe,Izadi等人,2011)©2011 IEEE。这三幅图像显示了原始(有噪声的)测距扫描、渲染为彩色法线贴图以及融合后的3D模型,同时渲染为法线贴图和Phong着色。
等,2011),该方法结合了类似ICP的SLAM技术——DTAM(Newcombe,Love- grove和Davison 2011),以及实时TSDF(截断有符号距离函数)体积积分,具体细节见第13.5.1节。后续论文包括用于非刚性对齐的弹性碎片(Zhou,Miller和Koltun 2013)、Oc- tomap(Hornung,Wurm等2013),后者使用八叉树和概率占用技术,以及Voxel Hashing(Nießner,Zollh fer等2013)和Chisel (Klingensmith,Dryanovski等2015),两者均采用空间哈希压缩TSDF。KinectFusion还扩展到
处理高度变化的扫描分辨率(Fuhrmann和Goesele 2011,2014)、动态场景(DynamicFusion (Newcombe,Fox,和Seitz 2015)、VolumeDeform (Innmann,Zollh fer等2016)和Motion2Fusion (Dou,Davidson等2017)),利用非刚性表面变形进行全局模型优化(ElasticFusion: Whelan,Salas- Moreno等2016),生成全局一致的BundleFusion
模型(Dai,Nießner
等,2017),并使用深度网络执行非刚性匹配(Bo i,Zollh fer
(et al.2020)。关于这些以及其他从RGB-D扫描构建3D模型的技术的更多细节,可参见Zollh fer、Stotko等人(2018)的综述。
最近的一些工作在范围数据合并中使用神经网络来表示TSDF (Park,Florence等,2019),用传入的范围数据扫描更新TSDF(Weder,Schonberger等,2020,2021),或提供局部先验(Chabra,Lenssen等,2020)。范围数据合并技术通常用于三维物体扫描以及视觉地图构建和导航(RGB-D SLAM),我们在第11.5节中讨论过。随着深度感知(如akalidar)技术开始出现在手机中,它可以用来构建完整的纹理映射3D房间模型,例如使用Occipital的Canvas应用程序(Stein 2020)。
基于带符号距离或特征(内部-外部)函数的体积范围数据合并技术也被广泛用于从定向或非定向点集提取平滑且行为良好的表面(Hoppe、DeRose等人,1992;Ohtake、Belyaev等人,2003;Kazhdan、Bolitho和Hoppe,2006;Lempitsky和Boykov,2007;Zach、Pock和Bischof,2007b;Zach,2008),详见第13.5.1节和Berger、Tagliasacchi等人(2017)的综述论文。
主动测距技术,结合表面建模和外观建模技术(第13.7节),在考古学和历史保护领域得到广泛应用,这些领域也常被称为数字遗产(MacDonald2006)。

图13.14吴哥-通的巴戎寺激光测距模型(Banno,Masuda
(et al.2008)©2008斯普林格出版社:(a)现场拍摄的照片;(b)从地面扫描的详细头部模型;(c)使用安装在气球上的激光测距传感器扫描的寺庙最终合并的3D模型。
此类应用中,获取文化物品的详细三维模型,然后用于分析、保存、修复和复制艺术品等应用(Rioux和Bird1993)。
一个显著的例子是莱沃伊、普利等人(2000年)的数字米开朗基罗项目,该项目使用了安装在大型龙门上的赛博韦激光条扫描仪和高质量数码单反相机,以获取佛罗伦萨米开朗基罗的大卫像及其他雕塑的详细扫描。该项目还对《罗马城市地图》进行了扫描,这是一张古代的罗马石质地图,已经破碎成碎片,通过数字技术重新匹配。整个过程,从最初的规划到软件开发、采集和后期处理,历时数年(并有许多志愿者参与),最终产生了丰富的三维形状和外观建模技术。
此后,更大规模的项目也已尝试,例如,对完整的寺庙遗址如吴哥窟(Ikeuchi和Sato2001;Ikeuchi和Miyazaki2007;Banno,Masuda等2008)进行扫描。图13.14显示了该项目的细节,包括一张样本照片、从地面水平扫描的详细3D(雕塑)头部模型,以及最终合并的3D遗址模型的航拍概览,该模型是通过气球获取的。
13.3 表面表示
在前面的章节中,我们已经看到了用于集成三维范围扫描的不同表示。现在我们详细地研究其中的一些表示。显式的表面表示,如三角网格、样条(Farin1992,2002)和细分曲面——
(Stollnitz、DeRose和Salesin 1996;Zorin、Schr der和Sweldens
1996;Warren和Weimer 2001;Peters和Reif 2008)不仅能够创建高度详细的模型,还能进行诸如插值(第13.3.1节)、平滑或优化以及降采样和简化(第13.3.2节)等处理操作。我们还探讨了基于离散点的表示方法(第13.4节)和体素表示方法(第13.5节)。
最常见的一种表面操作是从一组稀疏数据约束中重建表面,即散点数据插值,我们在第4.1节中讨论过。在构建这类问题时,表面可以参数化为高度场f (x),三维参数曲面f (x),或非参数模型,如三角形集合。
在第4.2节中,我们探讨了如何将二维函数插值和逼近问题{di }→f (x)转化为使用正则化(4.18–4.23)的能量最小化问题。这类问题还可以指定表面不连续点的位置以及局部方向约束(Terzopoulos1986b;Zhang,Dugas-Phocion等2002)。
解决此类问题的一种方法是使用有限元分析(4.24–4.27)在离散网格或网格上对表面和能量进行离散化(Terzopoulos 1986b)。然后可以使用稀疏系统求解技术,如多重网格法(Briggs、Henson和McCormick 2000)或层次预条件共轭梯度法(Szeliski 2006b;Krishnan和Szeliski 2011;Krishnan、Fattal和Szeliski 2013)来求解这些问题。表面也可以通过多级B样条的层次组合表示(Lee、Wolberg和Shin 1997)。
一种替代方法是使用径向基(或核)函数(Boult和Kender 1986;Nielson 1993),我们在Section4.1.1中已经讨论过。正如我们在该部分提到的,如果我们希望函数f(x)能够精确插值数据点,则必须求解一个稠密线性系统来确定每个基函数的权重(Boult和Kender 1986)。事实证明,对于某些正则化问题,例如(4.18–4.21),存在一些径向基函数(核)可以给出与完整解析解相同的结果(Boult和Kender 1986)。不幸的是,由于稠密系统的求解量级与数据点数量呈立方关系,基函数方法只能用于小规模问题,如基于特征的图像变形(Beier和Neely 1992)。
当建模三维参数曲面时,向量值函数f在(4.18–4.27)中编码了曲面上的3D坐标(x,y,z),而域x =(s,t)则编码了曲面的参数化。这类曲面的一个例子是寻求对称性的参数模型,这些模型是广义圆柱体的弹性变形版本。
d7(Terzopoulos、Witkin和Kass1987)。在这些模型中,s是沿可变形管脊的参数,t是围绕管的参数。为了在基于图像的轮廓曲线拟合过程中约束模型,使用了多种平滑性和径向对称力。
也可以定义非参数表面模型,例如一般的三角化网格,并通过有限元分析为这些网格配备内部平滑度指标和外部数据拟合指标(Sander和Zucker 1990;Fua和Sander 1992;Delingette、Hebert和Ikeuichi 1992;McInerney和Terzopoulos 1993)。虽然大多数方法假设标准的弹性变形模型,该模型使用二次内部平滑度项,但也可以使用次线性能量模型来更好地保留表面褶皱(Diebel、Thrun和Br nig 2006),或者使用图卷积神经网络(GCNNs)作为更新方程的替代方案,如深度主动表面模型(Wickramasinghe、Fua和Knott 2021)。三角网格还可以通过添加样条元素(Sullivan和Ponce 1998)或细分曲面(Stollnitz、DeRose和Salesin 1996;Zorin、Schrader和Sweldens 1996;Warren和Weimer 2001;Peters和Reif 2008)来生成具有更好平滑度控制的表面。
参数化和非参数化表面模型都假设表面的拓扑结构事先已知且固定。为了实现更灵活的表面建模,我们可以将表面表示为一组定向点(第13.4节)或使用三维隐函数(第13.5.1节),这些方法还可以与弹性三维表面模型结合使用(McInerney和Terzopoulos 1993)。
从无组织点样本中重建表面的领域继续迅速发展,最近的工作解决了数据缺陷问题,如Berger、Tagliasacchi等人(2017)的调查所述。
一旦从3D数据创建了三角网格,通常希望创建一个网格模型的层次结构,例如,在计算机图形应用程序中控制显示的细节级别(LOD)。(本质上,这是图像金字塔的三维类比(第3.5节)。)一种方法是用具有细分连接性的网格来近似给定的网格,然后可以计算一组三角小波系数(Eck,DeRose等,1995)。更连续的方法是使用顺序边折叠操作,从原始高分辨率网格过渡到粗略的基础级网格(Hoppe,1996;Lee,

图13.15飞机模型的渐进式网格表示(Hoppe1996)©1996
ACM:(a) base网格M0 (150个面);(b) mesh M 175 (500个面);(c) mesh M425(1000个面);(d)原始网格M=Mn(13546个面)。
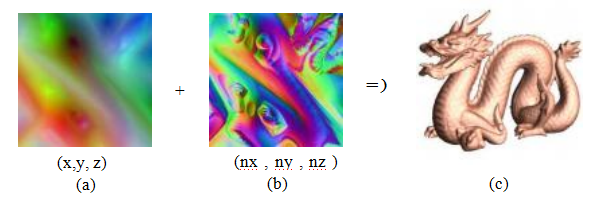
图13.16几何图像(Gu、Gortler和Hoppe 2002)©2002 ACM:(a)257×257的几何图像定义了表面的法线;(b)512×512的法线贴图定义了顶点法线;(c)最终的光照3D模型。
Sweldens等人于1998年提出)。由此产生的渐进网格(PM)表示可以用于以任意细节层次渲染3D模型,如图13.15所示。关于多分辨率几何建模的最新论文可以在Floater和Hormann(2005)的综述以及Dodgson、Floater和Sabin(2005)编辑的论文集中找到。
尽管Eck、DeRose等人(1995)、Hoppe(1996)和Lee、Sweldens等人(1998)提出的多分辨率表面表示方法支持细节层次操作,但它们仍然由不规则的三角形集合组成,这使得它们更难以以缓存高效的方式进行压缩和存储。8
为了使三角剖分完全规则(均匀且网格化),Gu、Gortler和Hoppe(2002)描述了如何通过沿精心选择的线切割表面网格并将其表示“展平”成一个正方形来创建几何图像。图13.16a显示了表面网格映射到单位正方形上的(x,y,z)值,而图13.16b则显示了相关的(nx,ny,nz)正法向量图,即与每个网格顶点关联的表面法向量,这可以用来补偿原始几何图像在高度压缩时视觉保真度的损失。
13.4 基于点的表示
正如我们之前提到的,基于三角形的表面模型假设三维模型的拓扑结构(以及通常的粗略形状)事先已知。虽然可以在变形或拟合过程中重新网格化模型,但更简单的解决方案是完全放弃显式的三角形网格,让三角形顶点作为定向点、粒子或表面元素(surfels)(Szeliski和Tonnesen 1992)。
为了赋予生成的粒子系统内部平滑约束,可以定义成对相互作用势能,这些势能近似于使用局部有限元分析获得的等效弹性弯曲能量。9不是提前为每个粒子(顶点)定义有限元邻域,而是使用软影响函数来耦合附近的粒子。由此产生的三维模型在演化过程中可以改变拓扑结构和粒子密度,因此可用于插值带有空洞的部分三维数据(Szeliski,Tonnesen和Terzopoulos 1993b)。表面方向和折痕曲线中的不连续性也可以建模(Szeliski,Tonnesen和Terzopoulos 1993a)。
为了将粒子系统渲染为连续表面,可以使用局部动态三角化启发式方法(Szeliski和Tonnesen 1992)或直接表面元素喷射(Pfister、Zwicker等2000)。另一种选择是首先将点云转换为隐式有符号距离或内外函数,使用最小有符号距离到定向点(Hoppe、DeRose等1992)或通过径向基函数插值特征(内外)函数(Turk和O‘Brien 2002;Dinh、Turk和Slabaugh 2002)。通过计算有符号距离函数的移动最小二乘(MLS)估计,可以获得更高的精度,包括处理不规则点密度的能力(Alexa、Behr等2003;Pauly、Keiser等2003),如图13.17所示。进一步改进可以通过局部球体拟合(Guennebaud和Gross 2007)、更快更准确的重采样(Guennebaud、Germann和
9如前所述,另一种方法是使用次线性相互作用势,这鼓励保存
表面压痕(Diebel、Thrun和Br nig,2006)。

图13.17基于点的表面建模与移动最小二乘法(MLS)(Pauly,Keiser等,2003)©2003 ACM:©一组点(黑点)转化为一个隐式内外函数(黑曲线);(b)最近定向点的有符号距离可以作为内外距离的近似;(c)一组具有可变采样密度的定向点,表示三维表面(头部模型);(d)用于移动最小二乘法的局部采样密度估计;(e)重建的连续三维表面。
Gross(2008)和核回归以更好地容忍异常值(Oztireli、Guennebaud和Gross,2008)。
伯杰、塔利亚萨奇等人(2017)的调查讨论了最近关于从点云重建平滑完整表面的工作。施普斯、萨特勒和波莱菲斯(2020)的《SurfelMeshing》论文介绍了一种基于可变分辨率表面元表示的
RGB-D SLAM系统,该系统在整合更多扫描时会重新三角化。郭、王等人(2020)的调查还讨论了使用深度学习的其他近期3D点云方法,这些方法在第5.5.1节中已有提及。本-沙巴特和古尔德(2020)以及朱和史密斯(2020)则介绍了更近期用于估计3D模型更好法线的算法。
13.5 容量表示
建模三维表面的第三种方法是构建三维体积内外函数。我们在第12.7.2节中已经看到了这种例子,当时我们探讨了体素着色(Seitz和Dyer 1999)、空间雕刻(Kutulakos和Seitz 2000)以及水平集(Pons、Keriven和Faugeras 2007)技术在立体匹配中的应用,而在第12.7.3节中,我们讨论了使用二值轮廓图像重建体积的方法。
在本节中,我们将研究连续隐式(内部-外部)函数来表示三维形状。
虽然多面体和体素表示可以任意精确地表示三维形状,但它们缺乏连续隐式曲面所具有的某些内在平滑特性。连续隐式曲面使用指示函数(或特征函数)F(x,y,z)来确定哪些3D点位于F(x,y,z)< 0内或位于F(x,y,z)> 0外。
早期使用隐式函数在计算机视觉中建模三维物体的例子是超二次曲面(Pentland 1986;Solina和Bajcsy 1990;Waithe和Ferrie 1991;Leonardis、Jakli和Solina 1997)。为了建模更多样化的
形状,超二次曲面通常与刚性或非刚性变形结合使用(Terzopoulos和Metaxas 1991;Metaxas和Terzopoulos 2002)。超二次曲面模型可以拟合到范围数据,也可以直接用于立体匹配。
通过在规则的三维网格上定义一个带符号的距离函数,可以构建另一种隐式形状模型,必要时使用八叉树样条来更粗略地表示远离其表面(零集)的函数(Lavall e和Szeliski 1995;Szeliski和Lavalle 1996;Frisken、Perry等2000;Ohtake、Belyaev等2003)。我们已经看到
了带符号距离函数用于表示
距离变换(第3.3.3节)、二维轮廓拟合和跟踪的水平集(第7.3.2节)、体积立体(第12.7.2节)、范围数据合并(第13.2.1节)以及基于点的建模(第13.4节)的例子。直接在网格上表示这些函数的优势在于,可以快速轻松地查找任何(x,y,z)位置的距离函数值,同时使用marching cubes算法提取等值面也很容易(Lorensen和Cline 1987)。Ohtake、Belyaev等(2003)的工作尤为突出,因为它允许使用多种距离。
这些功能可以同时使用,然后在本地组合起来产生尖锐的特征,如折痕。
表面泊松重建(Kazhdan、Bolitho和Hoppe 2006;Kazhdan和Hoppe 2013)使用了一个密切相关体积函数,即平滑的0/1内外(特征或占据)函数,可以将其视为一个裁剪后的带符号距离函数。该函数的梯度设置为沿着已知表面点附近的定向表面法线方向,并在其他地方设为0。该函数本身通过八叉树上的二次张量积B样条表示,这提供了一种紧凑的表示方法,在远离表面或点密度较低的区域使用较大的单元格,并且能够高效地求解相关的泊松方程(4.24–4.27),例如第8.4.4节和P rez、Gangnet和Blake(2003)。
也可以用L1(总变分)约束来代替泊松方程中使用的二次惩罚,仍然可以获得一个凸优化问题,这可以

图13.18像素对齐隐式函数(PIFu)网络可以从单个输入图像中恢复穿着衣服的人的高分辨率三维纹理模型(Saito,Huang et al.2019)©2019 IEEE。
使用连续(Zach,Pock和Bischof2007b;Zach2008)或离散图切割(Lempitsky和Boykov2007)技术解决。
有符号距离函数在水平集演化方程中也起着重要作用(第7.3.2节和第12.7.2节),其中网格上的距离变换值随着表面演化而更新,以适应多视图立体照片一致性测量(Faugeras和Keriven 1998)。
与计算机视觉的许多其他领域一样,深度神经网络也开始应用于体积对象表示的构建和建模。一些神经网络从单张图像中构建三维表面或体积占用网格模型(Choy、Xu等2016;Tatarchenko、Dosovitskiy和Brox 2017;Groueix、Fisher等2018;Richter和Roth 2018),尽管最近的实验表明,这些网络可能只是识别一般对象类别并进行少量拟合(Tatarchenko、Richter等2019)。DeepSDFs (Park、Florence等2019)、IM-NET (Chen和Zhang 2019)、occupancy Networks (Mescheder、Oechsle等2019)、deep Implicit Surface(DISN)网络(Xu、Wang等2019)以及UCLID-Net (Guillard、Remelli和Fua 2020)训练网络将连续的(x;y;z)输入转换为有符号距离或[0;1]占据值,有时结合卷积图像编码器与多层感知机来表示颜色和表面细节(Oechsle、Mescheder等2019),而MeshSDF可以连续地将SDF转换为可变形网格(Remelli、Lukoianov等2020)。所有这些网络都使用潜在代码来表示来自ShapeNet数据集中的通用类别的单个实例(例如汽车或椅子)(Chang、Funkhouser等2015),尽管它们在网络的不同部分使用这些代码(要么在输入中,要么通过条件批量归一化)。这使得它们能够仅从一张图像重建3D模型。
像素对齐的隐式函数(PIFu)网络将全卷积图像特征与神经隐式函数结合起来,以更好地保存局部形状和颜色细节(Saito,
黄等人2019;佐藤、西蒙等人2020)。他们专门针对穿着衣物的人类进行训练,仅凭一张彩色图像就能生成完整的3D模型(图13.18)。神经辐射场(NeRF)将这一技术扩展到使用像素光线方向作为输入,并输出连续的不透明度和辐射值,从而能够通过光线追踪渲染从多个输入图像构建的闪亮3D模型(米尔登霍尔、斯里尼瓦桑等人2020)。这种表示方法与光图和表面光场有关,我们将在第14.3节中详细讨论。这两种系统都是神经渲染方法的例子,用于生成逼真的新视角,我们将在第14.6节中更详细地讨论。
为了处理更大规模(例如建筑规模)的场景,卷积占用网络(Peng,Niemeyer等,2020)首先从二维、多平面或三维网格中提取局部特征,然后使用训练好的MLP(全连接网络)将这些特征解码为局部占用体积。与建模完整的三维场景不同,局部隐式网格表示(Jiang,Sud等,2020)建模小的局部子体积,使其可以作为其他形状重建方法的一种先验。
13.6 基于模型的重建
当我们提前了解要建模的对象时,可以使用专门的技术和表示方法构建更详细、更可靠的三维模型。例如,建筑通常由大型平面区域和其他参数形式(如旋转曲面)组成,这些形状通常垂直于重力方向且相互垂直(第13.6.1节)。头部和面部可以用低维的非刚性形状模型来表示,因为尽管人类面部的形状和外观变化极大,但仍然有界(第13.6.2节)。人体或其部分,如手,形成高度关节化的结构,可以使用由关节连接的分段刚性骨骼元素组成的运动链来表示(第13.6.4节)。
在本节中,我们重点介绍了用于这三种情况的一些主要思想、表示方法和建模算法。更多详细信息和参考文献可以在专门讨论这些主题的会议和研讨会上找到,例如国际三维视觉会议(3DV)和IEEE国际自动面部与手势识别会议(FG)。
13.6.1建筑
建筑模型,特别是从航拍照片中获得的模型,一直是研究时间最长的领域之一。
在摄影测量和计算机视觉中都存在这些问题(Walker和Herman,1988)。在

图13.19使用Fac¸ade系统进行交互式建筑建模(Debevec,Taylor,
(Malik1996)©1996 ACM:(a)输入图像中用户绘制的边缘显示为绿色;(b)阴影的3D实体模型;(c)几何图元叠加在输入图像上;(d)最终视图依赖的纹理映射3D模型。
在过去的二十年里,可靠的基于图像的建模技术的发展,以及数码相机和3D电脑游戏的普及,导致了这种系统的广泛应用。
德贝韦克、泰勒和马利克(1996)的工作是最早的混合几何和图像建模及渲染系统之一。他们的Fac¸ade系统结合了交互式图像引导的几何建模工具与基于模型的(局部平面加视差)立体匹配以及视图依赖的纹理映射。在交互式摄影测量建模阶段,用户选择块元素并将其边缘与输入图像中的可见边缘对齐(图13.19a)。然后,系统使用约束优化自动计算块的尺寸和位置以及相机位置(图13.19b-c)。这种方法本质上比一般特征基础的运动结构更可靠,因为它利用了块原始形状中的强大几何信息。贝克尔和博夫(1995)、霍里、安吉奥和阿莱(1997)、克里米尼西、里德和齐瑟曼(2000)以及霍林斯基、格拉蒂等人(2020)的相关工作也利用了类似的信息,这些信息来自消失点。辛哈、斯特迪等人(2008)的交互式图像建模系统中,使用消失点方向指导用户绘制多边形,这些多边形随后自动拟合到通过运动结构恢复的稀疏3D点。
一旦粗略的几何形状被估算出来,就可以使用局部平面扫描为每个平面面计算更详细的偏移图,Debevec、Taylor和Malik(1996)称之为基于模型的立体。最后,在渲染过程中,随着摄像机在场景中移动,来自不同视角的图像会被扭曲并混合在一起,这一过程(与光线有关
场和Lumigraph渲染;参见第14.3节)称为视图依赖纹理映射(图13.19d)。

图13.20全景图交互式3D建模(Shum、Han和Szeliski1998)©1998 IEEE:(a)带有用户绘制的垂直和水平(轴对齐)线的全景图广角视图;(b)走廊的单视重建。
对于室内建模,与其使用单张图片,不如使用全景图更为有用,因为这样可以看到更大的墙面和其他结构。舒姆、韩和斯泽利斯基(1998)开发的3D建模系统首先从多张图像中构建校准的全景图(第11.4.2节),然后让用户在图像中绘制垂直和水平线以划分平面区域的边界。这些线条最初用于确定每个全景图的绝对旋转角度,之后则与推断出的顶点和平面一起用于优化3D结构,该结构可以从一张或多张图像按比例恢复(图13.20)。近年来深度网络的进步使得自动推断线条及其连接点成为可能(黄、王等2018;张、李等2019),并能够构建完整的3D线框模型(周、齐、马2019;周、齐等2019b)。360°高动态范围全景图也可用于室外建模,因为它们能提供相对相机方向和消失点方向的高度可靠估计(安托内和特勒2002;特勒、安托内等2003)。
虽然早期基于图像的建模系统需要一些用户创作,但沃纳和齐瑟曼(2002)提出了一种完全自动化的线基重建系统。如第11.4.8节所述,他们首先检测线条和消失点,并用它们来校准相机;然后通过外观匹配和三焦张量建立线对应关系,这使他们能够重建一系列三维线段。接着,他们生成平面假设,使用共面的三维线和基于兴趣点处交叉相关得分的平面扫描(第12.1.2节)。平面的交点用于确定每个平面的范围,即初步粗略的几何形状,随后通过添加矩形或楔形凹陷和凸起进行细化。请注意,当有建筑物的俯视图可用时,这些可以进一步用于

图13.21使用3D线和面进行自动结构重建(Sinha、Steedly和Szeliski,2009)©2009 IEEE。
限制了三维建模过程(Robertson和Cipolla,2002年,2009年)。使用匹配的三维线来估计消失点方向和主要平面的想法被用于多个完全自动化的基于图像的建筑建模系统(Zebedin和Bauer
等,2008;Mi u k和Ko eck,2009
;Furukawa、Curless等,2009b;Sinha、Steedly,
以及Szeliski2009;Holynski、Geraghty等人2020)和SLAM系统(Zhou、Zou等人2015;Li、Yao等人2018;Yang和Scherer2019)。图13.21显示了Sinha、Steedly和Szeliski(2009)开发的系统中的一些处理阶段。
建筑的另一个共同特征是重复使用诸如窗户、门和柱廊等基本元素。建筑设计系统可以设计用于搜索这些重复元素,并将其作为结构推断过程的一部分(Dick,Torr和Cipolla 2004;Mueller,Zeng等2007;Schindler,Krishnamurthy等2008;Pauly,Mitra等2008;Sinha,Steedly等2008)。近年来,将平行线、交叉点和矩形等结构化元素与全轴对齐的三维模型结合用于建筑环境建模的方法被称为整体3D重建。更多细节可以在周、古川和马(2019)的最新教程、研讨会(周、古川等2020)以及平托雷、穆拉等(2020)的最新报告中找到。
这些技术的结合现在使得重建大型3D场景结构成为可能(Zhu和Kanade,2008)。例如,Pollefeys、Nist等人(2008)的Urbanscan系统利用装有GPS的车辆获取的视频,重建城市街道的纹理映射3D
模型。为了实现实时性能,他们不仅使用了优化的在线运动结构算法,还采用了GPU实现的平面扫描立体对齐到主平面和深度图融合的方法。Cornelis、Leibe等人(2008)提出了一种相关的系统,同样使用平面扫描立体(对齐到垂直构建-
infinac¸ades)结合了车辆的物体识别和分割。Mi u k和
Ko eck(2009
)利用全向图像和基于超像素的立体匹配沿主导平面方向,直接从主动测距重建。

图13.22三维模型拟合图像集合:(Pighin,Hecker等,1998)©
1998年ACM:(a)五张输入图像以及用户选择的关键点;(b)完整的键点和曲线集;(c)三个网格——原始网格、经过13个关键点调整后的网格,以及经过额外99个关键点调整后的网格;(d)将图像划分为可单独动画化的区域。
扫描数据与补偿了曝光和光照变化的彩色图像相结合也是可能的(Chen和Chen2008;Stamos、Liu等2008;Troccoli和Allen2008)。
许多基于这些计算机视觉技术的摄影测量重建系统已经开发出能够生成详细纹理映射的3D模型。10例如,可以用于从航拍无人机和地面摄影中重建大规模3D模型的商业软件包括Pix4D、11 Metashape、12和RealityCapture。13另一个例子是Occipital的Canvas手机应用程序14(Stein2020),该应用似乎结合了摄影测量(3D点和线匹配及重建,如
如上所述)和深度图融合。
13.6.2面部建模和跟踪
另一个领域中,专门的形状和外观模型极为有用,即头部和面部的建模。尽管乍看之下人的外貌似乎无穷无尽的变化,但一个人的头部和面部的实际形状可以用几十个参数来合理地描述(Pighin,Hecker等1998;Guenter,Grimm等1998;DeCarlo,Metaxas和Stone 1998;Blanz和Vetter 1999;Shan,Liu和Zhang 2001;Zollh fer,Thies等2018;Egger,Smith等2020)。
图13.22展示了一个基于图像的建模系统示例,用户在多张图像中指定的关键点用于将通用头部模型拟合到人脸。如图13.22c所示,在指定超过100个关键点后,面部形状变得非常适应且可识别。从原始图像中提取纹理贴图并应用到头部模型上,可以生成具有惊人视觉保真度的可动画模型(图13.23a)。
通过将主成分分析(PCA)应用于一组3D扫描的人脸,可以构建一个更强大的系统,这一主题我们在第13.6.3节中讨论。如图13.25所示,可以将可变形的3D模型拟合到单张图像,并利用这些模型进行各种动画和视觉效果(Blanz和Vetter 1999;Egger、Smith等2020)。还可以设计立体匹配算法,直接优化头部模型参数(Shan、Liu和Zhang 2001;Kang和Jones 2002),或使用实时立体成像与主动照明的输出(Zhang、Snavely等2004)(图13.10和13.23b)。
随着3D面部捕捉系统的复杂度提升,重建模型的细节和真实感也随之增强。现代系统不仅能够实时捕捉表面细节,如皱纹和褶皱,还能精确模拟皮肤反射、半透明度和次表层散射(Debevec,Hawkins等,2000;Weyrich,Matusik等,2006;Golovinskiy,Matusik等,2006;Bickel,Botsch等,2007;Igarashi,Nishino,和Nayar,2007;Meka,Haene等,2019)。
一旦构建了3D头部模型,它就可以用于多种应用中,例如头部追踪(Toyama 1998;Lepetit、Pilet和Fua 2004;Matthews、Xiao和Baker 2007),如图7.30所示,以及面部转移,即在视频中用一个人的脸替换另一个人的脸(Bregler、Covell和Slaney 1997;Vlasic、Brand等2005)。其他应用还包括通过扭曲面部图像使其更加吸引人来美化面部。

图13.23头部和表情跟踪及使用可变形3D模型的再动画。(a)模型直接拟合到五个输入视频流(Pighin、Szeliski和Salesin 2002)©2002斯普林格出版社:底部一行显示了根据顶部一行输入图像拟合姿态和表情参数的合成纹理映射3D模型的再动画结果。(b)模型拟合到帧率时空立体表面模型(Zhang、Snavely等2004)©2004 ACM:顶部一行显示了叠加了合成绿色标记的输入图像,而底部一行显示了拟合的3D表面模型。
有“标准”(Leyvand、Cohen-Or等人,2008年)、用于隐私保护的面部去识别(Gross、Sweeney等人,2008年)和面部交换(Bitouk、Kumar等人,2008年)。
近年来,3D头部模型的应用包括用于视频会议的逼真虚拟形象(Chu,Ma等,2020),用于自拍优化的3D解压(Fried,Shechtman等,2016;Zhao,Huang等,2019;Ma,Lin等,2020),以及单张照片肖像重照明(Sun,Barron等,2019;Zhou,Hadap等,2019;Zhang,Barron等,2020),图13.24展示了其中一个应用。最后一个应用作为“肖像光”功能出现在Google相册中。此外,Zollh fer,Thies等(2018)和Egger,Smith等(2020)的综述论文中还发现了其他15个应用。
13.6.3应用:面部动画
也许3D头部建模最广泛的应用是面部动画(Zollh fer,Thies等,2018)。一旦构建了一个人
头部形状和外观(表面纹理)的参数化3D模型,就可以直接用于追踪人的面部动作(图13.23a),并用这些相同的动作来动画化不同的角色。

图13.24人像阴影去除和处理(Zhang,Barron等,2020)©2020 ACM。上排显示原始照片,下排显示模拟出更讨人喜欢的光线后的相应增强照片。
以及表达式(Pighin、Szeliski和Salesin2002)。
可以构建这种系统的改进版本,首先将主成分分析(PCA)应用于可能的头部形状和面部外观的空间。Blanz和Vetter(1999)描述了一个系统,他们首先捕捉了一组200个彩色范围扫描。
面部(图13.25a),可以表示为大量(X,Y,Z,R,G,B)样本(vertices).16为了使三维变形有意义,不同人的扫描中相应的顶点必须首先对应起来(Pighin,Hecker等,1998)。一旦完成这一步,就可以应用主成分分析更自然地参数化三维可变形模型。通过在不同子区域进行单独分析,如眼睛、鼻子和嘴巴,可以增加该模型的灵活性,就像模块化特征空间中的方法一样(Moghaddam和Pentland,1997)。
计算出子空间表示后,该空间中的不同方向可以与不同的特征相关联,例如性别、面部表情或面部特征(图13.25a)。正如Rowland和Perrett(1995)的研究中所述,通过夸大人脸与平均图像的位移,可以将其转化为漫画形象。
3D可变形模型可以通过梯度下降法拟合到单张图像上,该方法基于输入图像与重新合成的模型图像之间的误差,在初始手动放置模型后,使其处于大致正确的姿态、比例和位置(图13.25b–c)。通过使用逆组合图像,可以提高此拟合过程的效率。
16圆柱坐标系为该集合提供了一个自然的二维嵌入,但这种嵌入对于执行PCA是不必要的。

图13.25三维可变形面部模型(Blanz和Vetter 1999)©1999 ACM:(a)原始的三维面部模型,在特定方向上增加了形状和纹理变化:偏离平均值(夸张)、性别、表情、体重和鼻形;(b)一个三维可变形模型拟合到单张图像,之后可以调整其重量或表情;(c)另一个三维重建的例子,以及一组不同的三维操作,如光照和姿态变化。

图13.26 3D可变形头模型的二十年时间线(Egger,Smith等,2020)©2020 ACM,包括Blanz和Vetter(1999)的原始论文结果、第一个公开可用的可变形模型(Paysan,Knothe等,2009)、面部重现结果(Kim,Garrido等,2018)以及基于GAN的模型(Gecer,Ploumpis等,2019)。
如Romdhani和Vetter(2003)所述的对齐(Baker和Matthews,2004)。
生成的纹理贴图3D模型可以进行修改,以产生多种视觉效果,包括改变人物的体重或表情,或者三维效果,如重新照明或基于3D视频的动画(第14.5.1节)。这些模型还可以用于视频压缩,例如仅传输少量面部表情和姿态参数来驱动合成虚拟形象(Eisert,Wiegand,和Girod2000;Gao,Chen等2003;Lombardi,Saragih等2018;Wei,Saragih等2019),或将静态肖像图像赋予生命(Averbuch-Elor,Cohen-Or等2017)。Egger,Smith等人(2020)关于3D可变形人脸模型的综述论文(图13.26)讨论了该领域的进一步研究和应用。
三维面部动画通常与演员的表演相匹配,这种技术被称为基于表演的动画(Section7.1.6)(Williams 1990)。传统的基于表演的动画系统使用标记式动作捕捉(Ma,Jones等2008),而一些较新的系统则利用深度相机或普通视频来控制动画(Buck,Finkelstein等2000;Pighin,Szeliski和Salesin 2002;Zhang,Snavely等2004;Vlasic,Brand等2005;Weise,Bouaziz等2011;Thies,Zollhofer等2016;Thies,Zollhofer等2018)。
后者的一个例子是为电影《本杰明·巴顿奇事》开发的系统,数字领域公司使用了Mova17的轮廓系统来捕捉演员布拉德·皮特的面部动作和表情(罗布和扎法2009)。轮廓技术结合了荧光颜料和多个高分辨率摄像机,实时捕捉演员的三维范围扫描。这些三维模型随后被转换成面部动作编码系统(FACS)的形状和表情参数(埃克曼和弗里森1978),以驱动不同的(较旧的)合成动画计算机生成图像(CGI)。
角色。Zollh fer、Thies等人(2018)的最新报告中可以找到更多关于性能驱动面部动画的例子。
13.6.4人体建模和跟踪
跟踪人类、建模其形状和外观以及识别其活动是计算机视觉领域中研究最为活跃的几个方面。每年的会议18和专门的期刊特刊(Hilton,Fua,and Ronfard2006)都致力于这一子领域。
以及两项调查(Forsyth、Arikan等人,2006年;Moeslund、Hilton和Krger,2006年)
列出超过400篇关于这些主题的论文。19人类Eva数据库包含多视角的人体动作视频序列,以及相应的动作捕捉数据、评估代码和基于粒子滤波的参考3D跟踪器。Sigal、Balan和Black(2010)的配套论文不仅描述了该数据库和评估方法,还对这一领域的重要工作进行了很好的综述。更近期的MPI FAUST数据集(Bogo、Romero等人,2014)包含300个人体扫描的真实高分辨率图像,并自动计算了真实对应关系;而更新的AMASS数据集(Mahmood、Ghorbani等人,2019)则拥有超过40小时的运动数据,涵盖了300多名受试者和11,000个动作。20
考虑到这一领域的广度,很难对所有这些研究进行分类,特别是
不同的技术通常相互补充。Moeslund、Hilton和Kr ger(2006)将
他们的调查涵盖了初始化、跟踪(包括背景建模和分割)、姿态估计以及动作(活动)识别。Forsyth、Arikan等人(2006)将他们的调查分为几个部分:跟踪(背景减除、可变形模板、流和概率模型)、从二维观察中恢复三维姿态、数据关联和身体部位。他们还包含了一个关于运动合成的部分,这部分在计算机图形学中研究得更为广泛(Arikan和Forsyth 2002;Kovar、Gleicher和Pighin 2002;Lee、Chai等人2002;Li、Wang和Shum 2002;Pullen和Bregler 2002):见第14.5.2节。该领域的另一潜在分类方法是根据输入是否使用二维或三维(或多视图)图像,以及是否使用二维或三维运动学模型。
在本节中,我们简要回顾了背景减除、初始化和检测、带流跟踪、三维运动学等领域中一些更具开创性和广泛引用的论文。
模型、概率模型、自适应形状建模和活动识别。我们建议读者参阅前面提到的综述,以了解其他主题和更多细节。
背景减除。许多人体跟踪系统的第一步是建模背景,以提取与人相对应的移动前景物体(轮廓)。Toyama、Krumm等人(1999)回顾了几种不同的抠图和背景维护(建模)技术,并对此主题进行了很好的介绍。Stauffer和Grimson(1999)描述了一些基于混合模型的技术,而Sidenbladh和Black(2003)则发展了一种更全面的方法,不仅建模背景图像统计特性,还建模前景物体的外观,例如它们的边缘和运动(帧差)统计特性。关于视频背景抠图的最新技术,如Sengupta、Jayaram等人(2020)和Lin、Ryabtsev等人(2021)的研究,在第10.4.5节的视频抠图部分有详细讨论。
一旦从一个或多个摄像头中提取出轮廓,就可以使用可变形模板或其他轮廓模型对其进行建模(Baumberg和Hogg 1996;Wren、Azarbayejani等1997)。随着时间的推移跟踪这些轮廓有助于分析场景中多人移动的情况,包括构建形状和外观模型,以及检测他们是否携带物体(Haritaoglu、Harwood和Davis 2000;Mittal和Davis 2003;Dimitrijevic、Lepetit和Fua 2006)。
初始化与检测。为了实现完全自动化的人员跟踪,首先需要在单个视频帧中检测(或重新获取)他们的存在。这一主题与行人检测密切相关,后者通常被视为一种物体识别(Mori,Ren等2004;Felzenszwalb和Huttenlocher 2005;Felzenszwalb,McAllester和Ra-manan 2008;Doll r,Wojek等2012;Doll r,Appel等2014;Sermanet,Kavukcuoglu等2013
;Ouyang和Wang 2013
;Tian,Luo等2015;Zhang,Lin等2016),因此将在第6.3.2节中进行更深入的讨论。基于2D图像初始化3D跟踪器的其他技术包括Howe,Leventon和Freeman(2000)、Ros-ales和Sclaroff(2000)、Shakhnarovich,Viola和Darrell(2003)、Sminchisescu,Kanaujia等(2005)、Agarwal和Triggs(2006)、Lee和Cohen(2006)、Sigal和Black(2006b)以及Stenger,Thayananthan等(2006)所描述的技术。
单帧人体检测和姿态估计算法可以独立用于执行跟踪(Ramanan、Forsyth和Zisserman 2005;Rogez、Rihan等2008;Bourdev和Malik 2009;G ler、Neverova和Kokkinos 2018;Cao、Hidalgo等2019),如第6.3.2节(图6.25)和第6.4.5节(图6.42–6.43)所述。然而,它们通常与帧间跟踪技术结合使用,以提供更好的可靠性。

图13.27跟踪三维人体运动:(a)人体手部的运动链模型(Rehg,Morris,和Kanade2003)©2003,经SAGE许可转载;(b)在视频序列中跟踪运动链的斑点模型(Bregler,Malik,和Pullen2004)©2004 Springer;(c-d)身体部位的概率松散肢体集合(Sigal,Bhatia等人2004)©2004 IEEE。
(Fossati、Dimitrijevic等人,2007;Andriluka、Roth和Schiele,2008;Ferrari、Marin-Jimenez和Zisserman,2008)。
跟踪与流。通过计算光流或匹配肢体外观来增强逐帧跟踪人员及其姿态的能力。例如,Ju、Black和Yacoob(1996)提出的纸板人模型将每条腿的部分(上部和下部)建模为移动的矩形,并使用光流估计其在每个后续帧中的位置。Cham和Rehg(1999)以及Sidenbladh、Black和Fleet(2000)利用光流和模板追踪肢体,同时采用处理多个假设和不确定性的技术。Bregler、Malik和Pullen(2004)使用完整的3D肢体和身体运动模型,具体描述如下。还可以将估计的运动场本身与某些原型匹配,以识别跑步动作的特定阶段,或将两个低分辨率视频片段进行匹配以实现视频替换(Efros、Berg等,2003)。基于流的跟踪也可用于追踪非刚性变形物体,如T恤(White、Crane和Forsyth,2007;Pilet,
Lepetit,和Fua2008;Furukawa和Ponce2008;Salzmann和Fua2010;Bo i,Zollh fer
等,2020;Bo i,Palafox等,2020,
2021)。也可以使用帧间运动
用于估计一个移动人的不断变化的纹理3D网格模型(de Aguiar,Stoll等人,2008)。
三维运动模型。使用更精确的人体形状和动作的三维模型可以大大提高人体建模和跟踪的有效性。这种表示方法在游戏和特效中的3D计算机动画中无处不在,
是一个运动模型或运动链,它规定了骨架中每个肢体的长度以及肢体或段之间的二维或三维旋转角度(图13.27a-b)。从可见表面点的位置推断关节角度的值称为逆运动学(IK),在计算机图形学中广泛研究。
图13.27a展示了Rehg、Morris和Kanade(2003)用于跟踪视频中手部运动的人类手部运动学模型。如你所见,手指与拇指之间的连接点有两个自由度,而指关节本身只有一个自由度。使用这种模型可以大大增强基于边缘的跟踪器处理快速运动、三维姿态的不确定性以及部分遮挡的能力。
可靠的实时手部跟踪和建模领域的一大进展是Kinect消费级RGB-D相机的引入(Sharp,Keskin等,2015;Taylor,Bor-deaux等,2016)。自那时起,常规RGB跟踪和建模也显著提升,新的技术利用神经网络提高了可靠性和速度(Zimmermann和Brox,2017;Mueller,Bernard等,2018;Hasson,Varol等,2019;Shan,Geng等,2020;Moon,Shiratori和Lee,2020;Moon,Yu等,2020;Spurr,Iqbal等,2020;Taheri,Ghorbani等,2020)。一些系统还结合了身体和手部跟踪,以更准确地捕捉人类的表情和活动(Romero,Tzionas和Black,2017;Joo,Simon和Sheikh,2018;Pavlakos,Choutas等,2019;Rong,Shiratori和Joo,2020)。
除了手部之外,运动链模型还被广泛用于全身建模和跟踪(O‘Rourke和Badler 1980;Hogg 1983;Rohr 1994)。一种流行的方法是为运动模型中的每个刚性肢体关联一个椭球体或超二次体,如图13.27b所示。然后可以将该模型拟合到一个或多个视频流的每一帧中,通过匹配从已知背景中提取的轮廓,或者通过匹配并跟踪遮挡边缘的位置(Gavrila和Davis 1996;Kakadiaris和Metaxas 2000;Bregler、Malik和Pullen 2004;Kehl和Van Gool 2006)。
实时骨骼追踪的一大突破是引入了用于互动视频游戏控制的Kinect消费级深度相机(Shotton,Fitzgibbon等,2011;Taylor,Shotton等,2012;Shotton,Girshick等,2013),如图13.28所示。在当前的骨骼追踪领域中,一些技术使用与2D测量相结合的2D模型,一些技术使用3D测量(范围数据或多视角视频)与3D模型结合(Baak,Mueller等,2011),还有一些技术利用单目视频直接推断和跟踪3D模型(Mehta,Sridhar等,2017;Habermann,Xu等,2019)。
也可以使用时间模型来改进周期性运动的跟踪,例如行走,通过分析关节角度随时间的变化(Polana和Nelson 1997;Seitz和Dyer 1997;Cutler和Davis 2000)。通过学习典型运动模式,可以提高这些技术的通用性和适用性,使用主成分分析。

图13.28 Kinect骨骼跟踪流程,包括逐像素的身体部位分类、身体关节假设,然后利用时间连续性和先验知识映射到骨骼(Shotton,Girshick等,2013)。该图摘自(Zhang,2012)©2012 IEEE。
消化(Sidenbladh、Black和Fleet2000;Urtasun、Fleet和Fua2006)。
概率模型。由于跟踪是一项极其困难的任务,因此通常会使用复杂的概率推断技术来估计被跟踪对象的可能状态。一种流行的方法称为粒子滤波(Isard和Blake 1998),最初是为跟踪人物和手部轮廓而开发的,如第7.3.1节所述。随后,该方法被应用于全身跟踪(Deutscher、Blake和Reid 2000;Sidenblad、Black和Fleet 2000;Deutscher和Reid 2005),并在现代跟踪器中继续使用(Ong、Micilotta等2006)。处理跟踪过程中固有的不确定性,还有其他方法,包括多假设跟踪(Cham和Rehg 1999)和膨胀协方差(Sminchisescu和Triggs 2001)。
图13.27c-d展示了一个复杂的时空概率图模型,称为松散肢体人,该模型不仅模拟了各肢体之间的几何关系,还模拟了它们可能的时间动态(Sigal,Bhatia等,2004)。各种肢体与时间点之间的条件概率从训练数据中学习得到,并使用粒子滤波进行最终的姿态推断。
自适应形状建模。全身建模和跟踪的另一个重要组成部分是将参数化形状模型拟合到视觉数据。正如我们在第13.6.3节(图13.25)中所见,大量注册的3D范围扫描可以用来创建可变形的形状和外观模型(Allen、Curless和Popovi 2003)。在此基础上,Anguelov、Srinivasan等人(2005)开发了一个名为scape(人物形状补全与动画)的复杂系统,该系统
首先获取不同姿势下大量人的范围扫描,然后对这些

图13.29使用参数化3D模型从单张图像估计人体形状和姿态(Guan,Weiss等人,2009)©2009 IEEE。
使用半自动标记放置的扫描。注册的数据集用于建模形状变化,作为个人特征和骨骼姿态的函数,例如,在某些关节弯曲时肌肉的突出(图13.29,上排)。由此产生的系统可用于形状补全,即从少量捕获的标记中恢复完整的3D网格模型,通过在形状和姿态空间中找到最佳模型参数来拟合测量数据。
因为该系统完全基于穿着紧身衣物的人的扫描数据构建,并使用参数化形状模型,所以无法处理穿着宽松衣物的人。B lan和Black(2008)通过估计同一人在多种姿态下观察到的视觉壳体内的身体形状来克服
这一限制,而Vlasic、Baran等人(2008)则调整了初始表面网格,使其更符合参数化形状模型,以更好地匹配视觉壳体。
虽然前面提到的身体拟合和姿态估计系统使用多个视角来估算身体形状,但Guan、Weiss等人(2009)则将一个人在自然背景下的单张图像拟合到一个人体形状和姿态模型中。通过手动初始化来估算大致的姿态(骨架)和高度模型,然后利用Grab Cut分割算法(第4.3.2节)对人的轮廓进行分割。接着,结合轮廓边缘线索和阴影信息(图13.29),对形状和姿态估计进行细化。最终生成的3D模型可用于创建新颖的动画。

图13.30使用Pavlakos、Choutas等人(2019)的SMPL-X模型从单张图像中提取全身、表情和手势特征。©2019 IEEE:(a)从单张图像中估计主要关节、骨骼、SMPL和SMPL-X模型;(b)SMPL-X对某些野外图像的定性结果。
虽然一些关于三维人体和姿态拟合的原始工作是使用SCAPE和BlendSCAPE (Hirshberg,Loper等,2012)模型完成的,但Loper、Mahmood等人(2015)开发的皮肤多个人线性模型(SMPL)引入了一种基于顶点的皮肤模型,能够准确表示自然人体姿势下的多种体型。该模型由静止姿态模板、姿态依赖混合形状和身份依赖混合形状组成,通过训练大量对齐的三维人体扫描数据构建而成。Bogo、Kanazawa等人(2016)展示了如何仅用单张图像通过他们的SMPLfy方法估计这个三维模型的参数。
在后续的研究中,罗梅罗、齐奥纳斯和布莱克(2017)通过增加一个具有关节和非刚性变形的手模型(MANO),扩展了这一模型。朱、西蒙和谢赫(2018)将SMPL身体模型与面部和手部模型结合,创建了能够追踪社交环境中多个人的3D弗兰克和亚当模型。帕夫拉科斯、肖塔斯等人(2019)利用数千个3D扫描数据训练了一个新的、统一的3D人体模型(SMPL-X),该模型扩展了SMPL,加入了性别特定的模型,并包括完全关节化的手和表情丰富的脸,如图13.30所示。他们还用变分自编码器(VAE)替换了SMPL中的高斯混合先验,并开发了一种新的VPoser先验,该先验是在马哈茂德、戈尔巴尼等人(2019)收集的大规模动作捕捉数据集上训练的。
在最近的研究中,Kocabas、Athanasiou和Black(2020)介绍了VIBE,这是一种利用AMASS进行人体姿态和形状视频推断的系统。Choutas、Pavlakos等人(2020)开发了一个他们称为ExPose(表达性姿态和形状回归)的系统,该系统可以直接从SMPL-X参数中回归出身体、面部和手部的参数。
RGB图像。最近的STAR(稀疏训练关节人体回归模型)(Osman,Bolkart,和Black2020)比SMPL参数少得多,并且消除了顶点之间的虚假长程相关性。它还包含依赖于身体姿态和BMI的形状依赖的姿态校正混合形状,通过额外训练10,000名男性和女性受试者的扫描数据来建模人类群体中更广泛的变化。GHUM和GHUML (Xu,Bazavan等2020)依赖于从深度变分自编码器构建的非线性形状空间来进行身体和面部变形,并使用归一化流表示来建模骨骼(身体和手)运动学。继续提高单张图像模型拟合精度和速度的最新论文包括Song,Chen,和Hilliges(2020)、Joo,Neverova,和Vedaldi(2020),以及Rong,Shiratori,和Joo(2020)。
活动识别。人类建模中最后广泛研究的主题是运动、活动和动作识别(Bobick 1997;Hu,Tan等2004;Hilton,Fua和Ronfard 2006)。常见的动作包括行走和跑步、跳跃、跳舞、捡起物品、坐下和站起来以及挥手。关于这些主题的论文包括Robertson和Reid(2006)、Sminchisescu,Kanaujia和Metaxas(2006)、Weinland,Ronfard和Boyer(2006)、Yilmaz和Shah(2006)以及Gorelick,Blank等(2007),还有我们在第6.5节讨论的更近期的视频理解论文,例如Carreira和Zisserman(2017)、Tran,Wang等(2018)、Tran,Wang等(2019)、Wu,Feichtenhofer等(2019)和Feichtenhofer,Fan等(2019)。
13.7 恢复纹理贴图和反照率
获取物体或人物的三维模型后,建模的最后一步通常是恢复纹理贴图以描述物体表面的外观。这首先需要建立一个参数化方法,将(u;v)纹理坐标作为三维表面位置的函数。一种简单的方法是为每个三角形(或一对三角形)关联一个单独的纹理贴图。更节省空间的技术包括将表面解包到一个或多个贴图上,例如使用细分网格(第13.3.2节)(Eck,DeRose等,1995年)或几何图像(第13.3.3节)(Gu,Gortler,和Hoppe,2002年)。
一旦每个三角形的(u;v)坐标被确定,透视投影就完成了。
从纹理(u;v)映射到图像j的像素(uj;vj)坐标的方程可以是
通过将仿射变换(u,v)→(X,Y,Z)与透视同构(X,Y,Z)→(uj,vj)连接获得(Szeliski和Shum 1997)。然后可以重新采样并存储(u,v)纹理图的颜色值,或者使用投影纹理映射将原始图像本身用作纹理源(OpenGL-ARB 1997)。
当有多个源图像可用于外观恢复时,情况变得更加复杂,这是常见的情况。一种方法是使用视图依赖纹理贴图(第14.1.1节),其中每个多边形面根据虚拟摄像机、表面法线和源图像之间的角度选择不同的源图像(Debevec,Taylor,和Malik 1996;Pighin,Hecker等1998)。另一种方法是为每个表面点估计完整的表面光场(Wood,Azuma等2000),如Section14.3.2所述。
在某些情况下,例如在传统3D游戏中使用模型时,最好在预处理过程中将所有源图像合并成一个单一的连贯纹理图(Weinhaus和Devarajan1997)。理想情况下,每个表面三角形应选择其最直接看到的地方(垂直于法线)的源图像,并且分辨率要与纹理图的最佳匹配。这可以表述为一个图割优化问题,其中平滑项鼓励相邻三角形使用相似的源图像,然后通过混合来补偿曝光差异(Lempitsky和Ivanov2007;Sinha、Steedy等人2008)。通过显式建模源图像之间的几何和光度错位,可以获得更好的结果(Shum和Szeliski2000;Gal、Wexler等人2010;Waechter、Moehrle和Goesele2014;Zhou和Koltun2014;Huang、Dai等人2017;Fu、Yan等人2018;Sch ps、Sattler和Pollefeys2019b;Lee、Ha等人2020)。“神经”纹理图表示也可以作为RGB颜色场的替代方案(Oechsle、Mescheder等人2019;Mihajlovic、Weder等人2021)。Zollh fer、Stotko等人(2018,第4.1节)更详细地讨论了相关技术。
这类方法在照明相对于物体固定时,即相机围绕物体或空间移动时,能够产生良好的效果。然而,当照明具有强烈的定向性,且物体相对于这种照明移动时,可能会出现强烈的阴影效应或镜面反射,这会干扰纹理(反照率)图的可靠恢复。在这种情况下,最好通过建模光源方向并估计表面反射特性来显式地消除阴影效应(第13.1节),同时恢复纹理图(佐藤和池内1996;佐藤、惠勒和池内1997;余和马利克1998;余、德贝韦克等人1999)。图13.31展示了这种方法的一个结果,在此过程中首先移除镜面反射,同时估计
2当表面以倾斜视角观察时,可能需要将不同的图像混合在一起以获得最佳分辨率(Wang,Kang等,2001)。

图13.31估算扫描3D模型的漫反射率和反射率参数(Sato、Wheeler和Ikeuchi,1997)©1997 ACM:(a)投射到模型上的输入图像集;(b)完整的漫反射(反照率)模型;(c)从反射率模型渲染出包括镜面成分的内容。
然后通过在Torrance-Sparrow反射模型(2.92)中估计镜面反射分量ks,重新引入了反射率成分(反照率)。
13.7.1估算BRDF
一种更为雄心勃勃的方法是针对视图依赖外观建模的问题,为物体表面的每个点估计一个通用的双向反射分布函数(BRDF)。Dana、van Ginneken等人(1999)、Jensen、Marschner等人(2001)和Lensch、Kautz等人(2003)提出了不同的技术来估计这些函数,而Dorsey、Rushmeier和Sillion(2007)以及Weyrich、Lawrence等人(2009)则提供了关于BRDF建模、恢复和渲染主题的综述。
正如我们在第2.2.2(2.82)节中所看到的,BRDF可以写成
fr (θi , φi , θr , φr ; λ), (13.6)
其中(θi,φi)和(θr,φr)是入射光线i和反射光线r的方向角
与图2.15所示的局部表面坐标系(x,y,)一起制作。当进行模态分析时
为了获得物体的外观,而不是材料的一块的外观,我们需要在物体表面的每一点(x,y)处估计这个函数,这给出了空间变化的BRDF或SVBRDF (Weyrich,Lawrence等,2009),
fv (x,y, θi , φi , θr , φr ; λ). (13.7)
如果要对次表面散射效应进行建模,例如,通过石膏等材料的长程光传输,则使用八维双向散射-表面反射分布函数(BSSRDF),
fe(xi,yi,θi,φi,xe,ye,θe,φe;λ), (13.8)

图13.32基于图像的外观和详细几何重建(Lensch,Kautz等,2003)©2003 ACM。(a)使用分裂聚类重新估计外观模型(BRDF)。(b)为了建模详细的、空间变化的外观,每个光子体被投影到由聚类材料形成的基底上。
其中esubscript现在代表发射而不是反射的光方向。
Weyrich、Lawrence等人(2009)对这些及相关主题进行了很好的综述,包括基本测光、BRDF模型、使用星等反射测量的传统BRDF获取方法,即精确测量视角和反射率(Marschner、Westin等人,2000;Dupuy和Jakob,2018),多路照明(Schechner、Nayar和Belhumeur,2009),皮肤建模(Debevec、Hawkins等人,2000;Weyrich、Matusik等人,2006),以及基于图像的获取技术,这些技术能够同时从多张照片中恢复物体的三维形状和反射率。
一个很好的例子是Lensch、Kautz等人(2003)开发的系统,他们估计局部变化的BRDF并使用表面法线的局部估计来优化其形状模型。为了构建模型,他们首先将每个表面点关联到一个包含三维位置、表面法线和一组稀疏辐射样本的光子体。接下来,他们利用拉福图恩反射模型(Lafortune,Foo等人1997)和分裂聚类方法(图13.32a),将这些光子体聚类成具有共同属性的材质。最后,为了建模详细的时空变化外观,每个光子体(表面点)被投影到聚类外观模型的基础之上(图13.32b)。Ma、Hawkins等人(2007)描述了一种更精确的法线估计系统,该系统使用偏振光照。
最近的方法用于恢复空间变化的BRDF(SVBRDF),要么从RGB-D扫描仪开始(Park、Newcombe和Seitz 2018;Schmitt、Donne等人2020),要么使用闪光/非闪光图像对(Aittala、Weyrich和Lehtinen 2015),或者采用深度学习方法同时估计表面法线和外观模型(Li、Sunkavalli和Chan-draeker 2018;Li、Xu等人2018)。更先进的系统还可以从测距扫描序列中估计形状和环境光照(Park、Holynski和Seitz 2020)或
单目图像(Boss,Jampani等,2020;Li,Shafiei等,2020;Chen,Nobuhara和Nishino,2020)甚至对这些场景进行重新照明(Bi,Xu等,2020a,b;Sang和Chandraker,2020;Bi,Xu等,2020c)。关于使用RGB-D摄像头捕捉物体的三维形状和外观的技术,可以参见Zollh fer,Stotko等(2018)的最新报告。
虽然本节中讨论的大多数技术需要大量的视图来估计表面特性,但一个有趣的挑战是将这些技术从实验室带到现实世界,并将它们与常规和基于互联网照片图像的建模方法结合起来。
13.7.2应用:三维模型采集
本章中描述的从多张图像构建完整3D模型并恢复其表面外观的技术,开辟了全新的应用领域,这些应用通常被称为3D摄影。Pollefeys和Van Gool(2002)以及Pollefeys、Van Gool等人(2004)对这类系统进行了很好的介绍,包括特征匹配、运动结构恢复、密集深度图估计、3D模型构建和纹理图恢复等处理步骤。Vergauwen和Van Gool(2006)以及Moons、Van Gool和Vergauwen(2010)描述了一个完整的基于网络的系统ARC3D,该系统能够自动执行所有这些任务。后者不仅深入综述了整个领域,还详细介绍了他们的端到端完整系统。
一个较新的商业摄影测量建模系统是Pix4D,该系统可用于物体和场景的捕捉。其网站展示了一个精彩的例子,即通过常规照片和航拍无人机照片重建的三维纹理映射城堡。智能手机的普及使得休闲3D摄影成为可能,例如Hedman、Alsisan等人(2017年)、Hedman和Kopf(2018年)以及Kopf、Matzen等人(2020年)的研究,这些内容将在第14.2.2节中详细描述。
替代完全自动化系统的另一种方法是让用户参与其中,这有时被称为交互式计算机视觉。早期的一个例子是由德贝韦克、泰勒和马利克(1996)开发的Fac¸adearchi-tectural建模系统。范登亨格尔、迪克等人(2007)描述了他们的VideoTrace系统,该系统能够自动进行点跟踪和从视频中恢复3D结构,然后允许用户在生成的点云上绘制三角形和表面,并且可以交互式地调整模型顶点的位置。辛哈、斯蒂迪等人(2008)描述了一个相关的系统,该系统使用匹配的消失点。
在多张图像中(图7.50)提取点以推断三维线的方向和平面法向量。这些信息随后用于指导用户绘制轴对齐的平面,这些平面会自动拟合到恢复的三维点云上。Zebe描述了这些想法的全自动变体——
din、Bauer等人(2008)、Furukawa、Curless等人(2009a)、Furukawa、Curless等人(2009b)、Mi
u k和Ko eck(2009)以及Sinha、Steedly和Szeliski(2009)。
随着这些技术的复杂性和可靠性的不断提高,我们可以期待看到更多用户友好的图像照片级真实感3D建模应用(练习13.8)。
13.8 附加阅读材料
形状从阴影中提取是计算机视觉中的经典问题之一(Horn 1975)。该领域的代表性论文包括霍恩(1977)、池内和霍恩(1981)、彭特兰(1984)、霍恩和布鲁克斯(1986)、霍恩(1990)、谢利斯基(1991a)、曼奇尼和沃尔夫(1992)、杜皮斯和奥利恩西斯(1994)以及福阿和勒克莱尔(1995)。霍恩和布鲁克斯(1989)编辑的论文集是这一主题的重要信息来源,特别是关于变分方法的章节。张、蔡等人(1999)的综述不仅回顾了这些技术,还提供了一些比较结果。
伍德汉姆(1981)撰写了光度立体的开创性论文。纹理形状技术包括威特金(1981)、池内(1981)、布洛斯坦和阿胡贾(1987)、格林(1992)、马利克和罗森霍尔
茨(1997)、刘、柯林斯和辛(2004)、刘、林和海斯(2004)、海斯、勒奥德亚努等人(2006)、林、海斯等人(2006)、洛贝和福赛思(2006)、怀特和福赛思(2006)、怀特、克兰和福赛思(2007)以及帕克、布罗克赫斯特等人(2009)。关于从失焦深度的优秀论文和书籍由彭特兰(1987)、奈亚尔和中川(1994)、奈亚尔、渡边和野口(1996)、渡边和奈亚尔(1998)、乔杜里和拉贾戈帕兰(1999)以及法瓦罗和索托(2006)撰写。沃尔夫、沙弗和希利编辑的《形状恢复》一书中讨论了从各种光照效果中恢复形状的其他技术,包括反射(奈亚尔、池内和卡纳德1991)。阿克曼和戈塞勒(2015)对光度立体进行了更近期的综述,最近的论文包括洛戈塞蒂、梅卡和奇波拉(2019)、黑夫纳、叶等人(2019)和桑托、韦克特和松下(2020)。
主动测距系统,使用激光或自然光照明投射到场景中,已被Besl(1989)、Rioux和Bird(1993)、Kang、Webb等人(1995)、Curless和Levoy(1995)、Curless和Levoy(1996)、Proesmans、Van Gool和Defoort(1998)、Bouguet和Perona(1999)、Curless(1999)、Hebert(2000)、Iddan和Ya- hav(2001)、Goesele、Fuchs和Seidel(2003)、Scharstein和Szeliski(2003)、Davis、Ra-
马莫思蒂和鲁辛凯维奇(2003),张、柯尔斯和塞茨(2003),张、斯纳维利等人(2004),以及穆恩斯、范古尔和维尔高温(2010),还有最近的综述文章,如张(2018)和池内、松下等人(2020)。单个范围扫描可以通过使用3D对应和距离优化技术进行对齐,例如迭代最近点及其变体(贝斯和麦凯1992;张1994;谢利斯基和拉瓦尔1996;约翰逊和康1997;戈德、兰加拉詹等人1998;约翰逊和赫伯特1999;普尔1999
;大卫、德门顿等人2004;李和哈特利2007;恩奎斯特、约瑟夫森和卡尔2009;波默勒、科拉斯和西格沃特2015;鲁辛凯维奇2019)。一旦它们被对齐,范围扫描可以使用建模表面到体积样本点的有符号距离的技术进行合并(霍普、德罗斯等人1992;柯尔斯和莱沃伊1996;希尔顿、斯托达特等人1996;惠勒、佐藤和池内1998;卡兹丹、博利索和霍普2006;伦皮茨基和博伊科夫2007;扎克、波克和Bischof2007b;Zach2008;Newcombe,伊扎迪等人2011;周、米勒和科尔图恩2013;纽科姆、福克斯和塞茨2015;佐尔费尔、斯托特科等人2018)。
一旦构建完成,3D表面可以使用多种三维表示方法进行建模和操作,这些方法包括三角网格(Eck,DeRose等,1995;Hoppe,1996),样条曲线(Farin,1992;Lee,Wolberg和Shin,1997;Farin,2002),细分曲面(Stollnitz,DeRose和Salesin,1996;Zorin,Schr der和Sweldens,1996;Warren
和Weimer,2001;Peters和Reif,2008),以及几何图像(Gu,Gortler和Hoppe,2002)。或者,它们也可以表示为带有局部方向估计的点样本集合(Hoppe,DeRose等,1992;Szeliski和Tonnesen,1992;Turk和O‘Brien,2002;Pfister,Zwicker等,2000;Alexa,Behr等,2003;Pauly,Keiser等,2003;Diebel,Thrun,
以及Br nig2006;Guennebaud和Gross2007;Guennebaud、Germann和Gross2008;
Oztireli、Guennebaud和Gross2008;Berger、Taglia-sacchi等人2017)。它们也可以使用在规则或不规则(八叉树)体网格上采样的隐式内外特征或有符号距离函数进行建模(Lavall e和Szeliski1995;Szeliski和Lavall e1996
;Frisken、Perry等人
2000;Dinh、Turk和Slabaugh2002;Kazhdan、Bolitho和Hoppe2006;Lempitsky和Boykov2007;Zach、Pock和Bischof2007b;Zach2008;Kazhdan和Hoppe2013)。
关于基于模型的三维重建文献非常丰富。对于建筑和城市场景的建模,已经开发出了交互式和全自动系统。专门讨论大规模三维场景重建的一期期刊(朱和卡纳德2008)是很好的参考来源,罗伯逊和奇波拉(2009)对一个完整的系统进行了精彩的描述。更多额外的参考文献可以在第13.6.1节中找到。
面部和全身建模与跟踪是计算机视觉领域一个非常活跃的分支,拥有自己的会议和研讨会,例如国际自动
面部和手势识别(FG)以及IEEE面部和手势分析与建模研讨会(AMFG)。关于3D人脸建模和跟踪的两篇最新综述论文分别是Zollh fer等人(2018年)和Egger、Smith等人(2020年),而关于全身建模
和跟踪的综述则包括Forsyth、Arikan等人(2006年)和Moeslund、Hilton,
以及Kr ger(2006)和Sigal、Balan和Black(2010)。
关于从多张彩色和RGB-D图像中恢复纹理图的一些代表性论文包括Gal、Wexler等人(2010年)、Waechter、Moehrle和Goesele(2014年)、Zhou和Koltun(2014年)以及Lee、Ha等人(2020年),还有Zollh fer、Stotko等人(2018
年,第4.1节)。更复杂的恢复空间变化BRDF的过程则由Dorsey、Rushmeier和Sillion(2007年)及Weyrich、Lawrence等人(2009年)的综述文章涵盖。最近能够使用较少图像和RGB-D图像实现这一目标的技术包括Aittala、Weyrich和Lehtinen(2015年)、Li、Sunkavalli和Chandraker(2018年)、Schmitt、Donne等人(2020年)以及Boss、Jampani等人(2020年)的研究,还有Zollh fer、Stotko等人(2018年
)的综述文章。
13.9 练习
例13.1:从焦点中获得形状。使用数码单反相机设置为手动对焦(或选择允许程序对焦控制的相机)拍摄一系列对焦图像,然后恢复物体的深度。
1.拍一些校准图像,例如棋盘格图像,以便计算失焦量和聚焦设置之间的映射关系。
2.尝试一个正面平行平面目标和一个倾斜的目标,以便覆盖传感器的工作范围。哪一个效果更好?
3.现在将一个真实对象放入场景中,并执行类似的聚焦扫描。
4.对于每个像素,计算局部锐度,并拟合聚焦设置上的抛物线曲线,以找到最聚焦的设置。
5.将这些焦点设置映射到深度,并将结果与真实值进行比较。如果你使用的是已知的简单对象,如球体或圆柱体(例如球或易拉罐),则
很容易测量它的真实形状。
6.(可选)看看你是否能从两三个焦点设置中恢复深度图。
7.(可选)使用液晶投影仪将人工纹理投射到场景上。使用一对摄像机比较焦点形状和立体技术形状的准确性。
Chapter 14 Image-based rendering
14.1视图插值 863
14.1.1视图依赖纹理贴图 865
14.1.2应用:摄影旅游 867
14.2层状深度图像 868
14.2.1假冒者、精灵和图层 869
14.2.2应用:3D摄影 872
14.3光场和光图 875
14.3.1非结构化Lumigraph 879
14.3.2表面光场 880
14.3.3应用:同心马赛克 882
14.3.4应用:合成重聚焦 883
14.4环境问题 883
14.4.1高维光场 885
14.4.2建模到渲染的连续过程 886
14.5基于视频的渲染 887
14.5.1基于视频的动画 888
14.5.2视频纹理 889
14.5.3应用:动画图片 892
14.5.4三维和自由视角视频 893
14.5.5应用:基于视频的漫游 896
14.6神经渲染 899
14.7附加阅读材料 908
14.8练习 910

图14.1基于图像和视频的渲染:(a)摄影旅游重建的3D视图(Snavely、Seitz和Szeliski 2006)©2006 ACM;(b)四维光场的一个切片(Gortler、Grzeszczuk等1996)©1996 ACM;(c)带有深度的精灵(Shade、Gortler等1998)©1998 ACM;(d)表面光场(Wood、Azuma等2000)©2000 ACM;(e)在新颖背景前的环境遮罩(Zongker、Werner等1999)©1999 ACM;(f)视频视图插值(Zitnick、Kang等2004)©2004 ACM;(g)用于重新激活旧视频的视频重写(Bregler、Covell和Slaney 1997)©1997 ACM;(h)蜡烛火焰的视频纹理(Sch dl、Szeliski等2000)©2000 ACM;(i)超时延视频,使用多个帧与3D代理拼接(Kopf、Cohen和Szel
在过去几十年中,基于图像的渲染已成为计算机视觉最令人兴奋的应用之一(Kang,Li等,2006;Shum,Chan和Kang,2007;Gallo,Troccoli等,2020)。在基于图像的渲染中,计算机视觉中的三维重建技术与计算机图形学渲染技术相结合,利用场景的多个视角来创建互动的照片级真实体验,如图14.1a所示的“照片旅游”系统。这类系统的商业版本包括在线地图系统如谷歌地图中的沉浸式街道导航,以及从大量随意获取的照片集合中创建3D照片合成。
在本章中,我们将探讨多种基于图像的渲染技术,如图14.1所示。我们首先介绍视图插值(第14.1节),它利用一个或多个预计算的深度图,在一对参考图像之间创建无缝过渡。与此概念密切相关的是视图依赖纹理贴图(第14.1.1节),它在3D模型表面融合多个纹理贴图。视图插值中用于颜色图像和3D几何的表示方法包括许多巧妙的变体,例如分层深度图像(第14.2节)和带有深度的精灵(Section14.2.1)。
我们继续探索基于图像的渲染,特别是场景外观的光场和Lumigraph四维表示(第14.3节),这些表示可以用于从任意视角渲染场景。这些表示的变体包括非结构化的Lumigraph(Section14.3.1)、表面光场(Section14.3.2)、同心马赛克(Section14.3.3)和环境遮罩(第14.4节)。
我们接着探讨基于视频的渲染技术,该技术利用一个或多个视频来创造新颖的视频体验(第14.5节)。涵盖的主题包括基于视频的人脸动画(第14.5.1节),以及视频纹理(第14.5.2节),其中短片段可以无缝循环播放,以创建场景的动态实时视频渲染。
我们继续讨论由多个视频流创建的3D视频(第14.5.4节),以及基于视频的环境漫游(第14.5.5节),这些技术已在沉浸式户外地图绘制和驾驶导航系统中得到广泛应用。本章最后回顾了神经渲染领域的最新研究(第14.6节),其中生成式神经网络被用于创建更逼真的静态场景、物体及人物重建。
14.1 视图插值
虽然基于图像的渲染一词最早出现在陈(1995)和麦克米伦与毕晓普(1995)的论文中,但陈与威廉姆斯(1993)关于视图插值的工作

图14.2视图插值(Chen和Williams1993)©1993 ACM:(a)来自一个源图像的孔洞(以蓝色显示);(b)结合两个间距较大的图像后的孔洞;(c)结合两个间距较近的图像后的孔洞;(d)插值后(孔洞填充)。
被认为是该领域的开创性论文。在视差插值中,渲染图像对与其预计算的深度图结合,生成插值视图,模拟虚拟摄像机在这两个参考视图之间的所见景象。自其最初提出以来,从捕获图像中新视角合成的整个领域一直是一个非常活跃的研究方向。关于这一主题的良好历史概述和最新成果可以在CVPR教程中找到(Gallo,Troccoli等,2020)。
视图插值结合了计算机视觉和计算机图形学中先前使用过的两个概念。第一个是将恢复的深度图与用于计算的参考图像配对,然后利用生成的纹理映射3D模型生成新的视图(图12.1)。第二个是变形的概念(第3.6.3节)(图3.51),其中利用图像对之间的对应关系,将每个参考图像扭曲到中间位置,同时在这两个扭曲后的图像之间进行交叉溶解。
图14.2更详细地展示了这一过程。首先,使用参考图像和虚拟3D相机姿态的知识以及每张图像的深度图(2.68–2.70),将两个源图像变形为新的视图。在陈和威廉姆斯(1993)的论文中,采用了一种前向变形算法(算法3.1和图3.45)。为了提高空间和渲染时间效率,深度图被表示为四叉树(Samet1989)。
在前向变形过程中,多个像素(相互遮挡)可能会落在同一个目标像素上。为了解决这一冲突,可以为每个目标像素关联一个z缓冲区深度值,或者按照后到前的顺序对图像进行变形,这可以根据极线几何知识计算得出(陈和威廉姆斯1993;拉沃和福热尔1994;麦克米伦和毕晓普1995)。
一旦两个参考图像被扭曲到新的视图(图14.2a-b),它们
可以合并以创建一个连贯的合成图(图14.2c)。每当其中一张图像有孔洞(用青色像素表示)时,另一张图像将作为最终值使用。当两张图像都有像素可以贡献时,这些像素可以根据虚拟相机和源相机之间的相对距离进行混合,就像通常的变形处理一样。请注意,如果两张图像的曝光度差异很大,这在对真实图像进行视图插值时可能会发生,那么填充孔洞的区域和混合后的区域将会有不同的曝光度,从而导致细微的伪影。
视图插值的最后一步(图14.2d)是填补由于前向变形过程或缺乏源数据(场景可见性)而产生的任何剩余孔洞或裂缝。这可以通过从孔洞附近的像素复制像素来完成。(否则,前景物体会受到“膨胀效应”的影响。)
上述过程对于刚性场景效果良好,尽管其视觉质量(无锯齿)可以通过两步前向后向算法(第14.2.1节)(Shade,Gortler等,1998年)或全三维渲染(Zitnick,Kang等,2004年)得到改善。当两个参考图像来自非刚性场景时,例如一张照片中的人微笑,另一张中则皱眉,可以使用视图变形技术,该技术结合了视图插值与常规变形的思想(Seitz和Dyer,1996年)。此外,还可以利用拟合到面部的深度图来合成远距离视角,消除“自拍”摄影中常见的放大鼻子和其他面部特征(Fried,Shechtman等,2016年)。
虽然最初的视图插值论文描述了如何基于相似的预计算(线性透视)图像生成新视图,但麦克米伦和毕晓普(1995)的全光子建模论文认为应使用圆柱形图像来存储预计算渲染或真实世界图像。陈(1995)也提出使用环境贴图(圆柱形、立方体或球形)作为视图插值的源图像。
视图依赖纹理贴图(Debevec、Taylor和Malik 1996)与视图插值密切相关。与其为每个输入图像关联单独的深度图,不如为场景创建一个单一的3D模型,但根据虚拟摄像机当前的位置使用不同的图像作为纹理贴图源(图14.3a)。
更详细地说,给定一个新的虚拟摄像机位置,将该摄像机对每个多边形(或像素)的视图与潜在源图像的视图进行比较。这些图像为
然后使用与角度αi成反比的加权进行混合

图14.3视图依赖纹理映射(Debevec、Taylor和Malik 1996)©1996 ACM。(a)每个输入视图的权重取决于新(虚拟)视图与原始视图之间的相对角度;(b)简化的三维模型几何结构;(c)在视图依赖纹理映射下,几何结构显得更加详细(凹陷的窗户)。
虚拟视图和源视图(图14.3a)。即使几何模型可以相当粗糙(图14.3b),不同视图的融合由于对应像素之间的视觉运动,仍能强烈地传达出更详细的几何信息。虽然原始论文在每个像素或粗化的多边形面上分别进行加权混合计算,但Debevec、Yu和Borshukov(1998)后续的工作提出了一种更高效的实现方法,该方法基于预计算各种视角空间部分的贡献,然后使用投影纹理映射(OpenGL-ARB1997)。
视图依赖纹理映射的概念已被广泛应用于后续的基于图像的渲染系统中,包括面部建模和动画(Pighin,Hecker等,1998)以及三维扫描和可视化(Pulli,Abi-Rached等,1998)。与视图依赖纹理映射密切相关的是,在四维空间中光线混合的概念,这是Lumigraph和非结构化Lumigraph系统的基础(第14.3节)(Gortler,Grzeszczuk等,1996;Buehler,Bosse等,2001)。
为了在他们的Fac¸ade系统中提供更加真实的视觉效果,Debevec、Taylor和Malik(1996)还加入了一个基于模型的立体组件,该组件为模型中的每个粗略平面面片计算一个偏移(视差)图。他们将这种分析和渲染系统称为混合几何与图像方法,因为它使用传统的3D几何建模来创建全局3D模型,然后利用局部深度偏移以及视图插值来增加视觉真实感。与逐像素扭曲深度图或较粗略的三角化几何(如第14.3.1节所述的非结构化Lumigraph)不同,也可以使用超像素作为被扭曲的基本单元(Chaurasia、Duchene等,2013)。固定规则的视图依赖混合也可以用深度神经网络替代,例如在深度
混合系统,由Hedman,Philip等人(2018)提出。

图14.4摄影旅游(Snavely、Seitz和Szeliski 2006)©2006 ACM:(a)场景的三维概览,平面替身上绘制了半透明的水洗效果和线条;(b)用户选择感兴趣区域后,底部会显示一组相关的缩略图;(c)用于最佳稳定的平面代理选择(Snavely、Garg等2008)©2008 ACM。
虽然视图插值最初是为了加速低功耗处理器和系统在没有图形加速的情况下渲染3D场景而开发的,但事实证明,它可以直接应用于大量随意获取的照片。斯纳维利、塞茨和谢利斯基(2006)开发的“照片旅游”系统利用运动结构计算所有拍摄图像的相机的3D位置和姿态,以及场景的稀疏3D点云模型(第11.4.6节,图11.17)。
为了对生成的图像海洋进行基于图像的探索(Aliaga,Funkhouser等,2003),照片旅游首先为每张图像关联一个三维代理。虽然从点云获得的三角化网格有时可以形成合适的代理,例如用于户外地形模型,但通常情况下,对每张图像中可见的三维点进行简单的主平面拟合效果更好,因为它不会包含任何作为伪影突出的错误段或连接。然而,随着自动三维建模技术的不断改进,天平可能会再次倾向于更详细的三维几何(Goesele,Snavely等,2007;Sinha,Steedly和Szeliski,2009)。一个例子是Goesele、Ackermann等(2010)开发的混合渲染系统,他们使用密集的每张图像深度图来重建每个图像中较为可靠的区域,并使用三维彩色点云来处理不太确定的区域。
生成的基于图像的导航系统允许用户从一张照片移动到另一张照片,既可以通过从场景的俯视图中选择相机(图14.4a),也可以通过在图像中选择感兴趣区域、导航至附近的视图或选择相关的缩略图(图14.4b)。为了创建3D场景的背景,例如当从上方观看时,可以使用非写实技术(第10.5.2节),如半透明的颜色渐变或
突出显示3D线段,可以使用(图14.4a)。系统还可以用于标注图像区域,并自动将此类注释传播到其他照片。
用于照片旅游和微软相关Photosynth系统的三维平面代理导致了非真实感的过渡,类似于“页面翻动”等视觉效果。选择所有平面的稳定三维轴可以减少漂移并增强三维感知(图14.4c) (Snavely,Garg等人,2008)。还可以自动检测场景中从多个视角看到的对象,并围绕这些对象创建“视点轨道”。此外,可以在三维位置和观看方向上的相邻图像之间建立链接,以创建“虚拟路径”,然后可以使用这些路径在任意图像对之间导航,例如你在热门旅游景点漫步时拍摄的照片(Snavely,Garg等人,2008)。这一想法进一步发展并作为谷歌地图的一项功能发布,称为照片之旅(Kushal,Self等人,2012)。这种合成虚拟视图的质量已经变得如此精确,以至于Shan,Adams等人(2013)提出了一种视觉图灵测试来区分合成图像和真实图像。Waechter,Beljan等人(2017)使用他们所谓的虚拟再摄影技术,对基于图像的建模和渲染系统进行了更高分辨率的质量评估。使用更近期的神经渲染技术可以获得进一步的改进(Hedman,Philip等人,2018;Meshry,Goldman等人,2019;Li,Xian等人,2020),我们将在第14.6节中讨论。
照片旅游技术对图像特征和区域的空间匹配,也可用于从大量图像集合中推断更多信息。例如,西蒙、斯纳维利和塞茨(2007)展示了如何利用热门旅游景点图像之间的匹配图来找到集合中最具标志性的(常被拍摄的)对象及其相关标签。在后续研究中,西蒙和塞茨(2008)展示了如何通过分析照片中心部分出现的3D点,将这些标签传播到每张图像的子区域。此外,还研究了将这些技术扩展到全球所有图像的可能性,包括在可用时使用GPS标签(李、吴等,2008;夸克、莱贝和范古尔,2008;克兰德尔、巴克斯特罗姆等,2009;李、克兰德尔和胡滕洛赫,2009;郑、赵等,2009;拉古拉姆、吴等,2011)。
14.2 层状深度图像
传统的视图插值技术将单个深度图与每个源或参考图像关联。不幸的是,当这样的深度图被扭曲到新视角时,会出现孔洞和

图14.5各种基于图像的渲染原语,根据相机与感兴趣对象之间的距离选择使用(Shade,Gortler等,1998)©1998 ACM。靠近的物体可能需要更详细的多边形表示,而中等距离的物体可以使用分层深度图像(LDI),远处的物体则可以使用精灵(可能带有深度信息)和环境贴图。
裂缝不可避免地出现在前景物体的后方。一种缓解此问题的方法是在参考图像中的每个像素处保留多个深度和颜色值(深度像素)(至少对于靠近前景-背景过渡的像素)(图14.5)。由此产生的数据结构称为分层深度图像(LDI),可以使用从后向前的前向变形(喷溅)算法渲染新的视图(Shade,Gortler等,1998)。
除了在每个像素处保存颜色深度值列表,如LDI中所做的那样,还可以将对象组织成不同的图层或精灵。精灵一词源自计算机游戏行业,在《吃豆人》或《马里奥兄弟》等游戏中用来指代平面动画角色。当这些对象被置于三维环境中时,通常被称为“假人”,因为它们使用了一块平坦的、带有透明度遮罩的几何图形来表示远离摄像机的三维物体的简化版本(Shade,Lischinski等,1996;Lengyel和Snyder,1997;Torborg和Kajiya,1996)。在计算机视觉中,这种表示通常称为图层(Wang和Adelson,1994;Baker、Szeliski和Anandan,1998;Torr、Szeliski,

图14.6深度精灵(Shade,Gortler等人,1998)©1998 ACM:(a)alpha蒙版颜色精灵;(b)相应的相对深度或视差;(c)没有相对深度的渲染;(d)有深度的渲染(注意弯曲的对象边界)。
以及Anandan1999;Birchfield、Natarajan和Tomasi2007)。第9.4.2节讨论了透明层和反射的问题,这些现象发生在镜面和透明表面上,如玻璃。
虽然平面层通常可以很好地表示远处物体的几何形状和外观,但通过建模每个像素相对于基平面的偏移量,可以获得更好的几何保真度,如图14.5和14.6a-b所示。这种表示方法在计算机视觉文献中被称为“平面加视差”(Kumar,Anandan,和Hanna1994;Sawhney1994;Szeliski与Coughlan 1997;Baker,Szeliski,和Anandan 1998),详见第9.4节(图9.14)。除了全自动立体技术外,还可以绘制深度层(Kang 1998;Oh,Chen等2001;Shum,Sun等2004),或从单目图像线索推断其三维结构(Sections6.4.4and 12.8)(Hoiem,Efros,和Hebert 2005b;Saxena,Sun,和Ng 2009)。
我们如何从一个新颖的视角渲染具有深度的精灵?一种方法,就像处理常规深度图一样,是将每个像素直接前向扭曲到新位置,这可能会导致锯齿和裂纹。更好的方法,我们在第3.6.2节中已经提到过,是首先将深度(或(u;v)位移)图扭曲到新视角,填补裂缝,然后使用高质量的逆向扭曲来重新采样颜色图像(Shade,Gortler等,1998)。图14.6d展示了这种两步渲染算法的结果。从这张静态图像中可以看出,前景精灵看起来更加圆润;然而,为了
要真正欣赏到现实主义的改进,你必须看看实际的动画序列。
深度精灵也可以使用常规图形硬件进行渲染,如(Zitnick,Kang等人,2004)所述。Rogmans,Lu等人(2009)描述了GPU实现的实时立体匹配和实时正向和反向渲染算法。

图14.7细切的前视平行层:(a)醋酸盐堆叠(Szeliski和Golland 1999)©1999斯普林格出版社和(b)多平面图像(Zhou,Tucker等2018)©2018 ACM。这些表示(等效)由一组固定深度的前视平行平面组成,每个平面编码一个RGB图像和一个alpha贴图,捕捉相应深度处的场景外观。
构建少量层的替代方法是将分层深度图像下的视场离散化为大量前平行平面,每个平面包含RGBA值(Szeliski和Golland 1999),如图14.7所示。这与我们在第12.1.2节和图12.6中介绍的平面扫描立体方法的空间表示相同,不同之处在于这里用于表示彩色3D场景,而不是累积匹配成本体积。这种表示本质上是包含RGB颜色和α不透明度值的体素表示的透视变体(第13.2.1节和第13.5节)。
这种表示方法最近被重新发现,现在广为人知的名字是多平面图像(MPI)(周、塔克等人,2018)。图14.8展示了一个从立体图像对派生的MPI表示,以及一个新颖的合成视图。与真正的(最小)层次表示相比,MPI更容易从立体图像对或集合中派生出来,因为平面上扫描成本体积(图12.5)中的像素(实际上是体素)与MPI之间存在一对一的对应关系。然而,它们不如后者紧凑,一旦视角超过一定范围,可能会导致撕裂伪影。(我们将在第14.2.2节讨论使用修复技术来减轻基于图像的表示中的这些孔洞)。MPI还与Penner和Zhang(2017)之前提出的软三维体积表示有关。
自最初开发用于新颖视图外推,即“立体放大”(Zhou,Tucker等,2018)以来,MPIs在基于图像的渲染中找到了广泛的应用,包括扩展到多输入图像和更快的推理(Flynn,Broxton等,2019),CNN精炼和更好的修复(Srinivasan,Tucker等,2019),以及跨

图14.8从彩色图像立体对构建的MPI表示,以及从MPI重建的新视角(周,塔克等,2018)©2018 ACM。请注意,这些平面将三维场景切分为薄层,每一层仅在小区域内具有颜色和完全或部分不透明度。
在MPI集合(Mildenhall,Srinivasan等,2019)和大视图外推(Choi,Gallo等,2019)之间进行权衡。平面MPI结构也被推广到曲面上,用于表示部分或完整的3D全景图(Broxton,Flynn等,2020;Attal,Ling等,2020;Lin,Xu等,2020)。
另一层应用的重要领域是反射建模。当反射面(例如玻璃板)为平面时,反射会形成一个虚拟图像,可以将其建模为单独的一层(第9.4.2节和图9.16–9.17),只要使用叠加(而非覆盖)合成方法来结合反射和透射图像(Szeliski、Avidan和Anandan 2000;Sinha、Kopf等2012;Kopf、Langguth等2013)。图14.9展示了一个从短视频片段重建的两层分解示例,可以通过添加两个层次的扭曲版本(每个层次都有自己的深度图)从新视角重新渲染。当反射表面弯曲时,可能仍可获得准稳定的虚拟图像,但这取决于局部主曲率的变化(Swaminathan、Kang等2002;Criminisi、Kang等2005)。反射建模是层状表示如MPIs的一个优势(Zhou、Tucker等2018;Broxton、Flynn等2020),尽管这些论文中仍然使用覆盖合成方法,这会导致合理但不物理正确的渲染结果。
在19世纪中期,人们渴望捕捉和观看三维世界的照片(Luo,Kong等人,2020年),最近又出现了立体相机和立体显示器。

图14.9使用多个加性层对带有反射的场景进行图像渲染(Sinha,Kopf等,2012)©2012 ACM。左列显示了输入序列中的一个图像,接下来两列分别展示了两个分离的层次(透射光和反射光)。最后一列是对场景中哪些部分是反射的部分的估计。如你所见,一些散射的反射有时会附着在透射光层上。请注意,在表格中,由于菲涅尔反射,反射光(光泽度)的数量随着图像底部的移动而减少。
3D电影的流行。它还支撑了我们在前一章,特别是第13.7.2节中研究的大部分关于3D形状和外观捕捉及建模的研究。然而,直到最近,虽然所需的多张图像可以用手持相机拍摄(Pollefeys,Van Gool等,2004;Snavely,Seitz和Szeliski,2006),但需要台式机或笔记本电脑来处理和交互查看这些图像。
近年来,捕捉、构建并广泛分享此类3D模型的能力显著提升,现在这一领域被称为3D摄影。Hedman、Alsisan等人(2017)描述了他们的Casual 3D摄影系统,该系统从移动摄像机拍摄一系列重叠图像,然后利用运动结构、多视图立体和3D图像变形与拼接技术,构建可在计算机上查看的两层部分全景图,如图14.10所示。即时

图14.10用于捕捉和建模手持照片中3D场景的系统。(a)随机3D摄影通过一系列重叠图像构建每张图像的深度图,然后将这些深度图扭曲并融合成两层表示(Hedman,Alsisan等,2017)©2017 ACM。(b)即时3D摄影从双镜头智能手机生成的深度图开始,扭曲和配准深度图以创建类似的表示,计算量大大减少(Hedman和Kopf,2018)©2018 ACM。(c)一拍3D摄影从单张照片开始,执行单目深度估计、图层构建和修复,以及网格和图集生成,实现基于手机的重建和交互式查看(Kopf,Matzen等,2020)©2020 ACM。
赫德曼和科普夫(2018)的3D系统构建了类似的体系,但起点是来自较新双摄像头智能手机的深度图像,以显著加快处理速度。然而,需要注意的是,单个深度图像是非度量的,即没有通过单一全局标量变换与真实深度关联,因此在拼接之前必须进行变形扭曲。随后构建纹理图集,以紧凑存储像素颜色值,同时支持多层。
虽然这些系统能够生成美丽的宽幅3D图像,营造出真正的沉浸感(“身临其境”),但使用单个深度图可以构建更实用且快速的解决方案。Kopf、Alsisan等人(2019)描述了他们的基于手机的系统,该系统通过拍摄一张双镜头照片并附带估计的深度图,构建一个多层3D照片,其中被遮挡的像素可以从附近的背景像素中填充(见第10.5.1节和Shih、Su等人2020)。为了消除与输入图像关联深度图的需求,Kopf、Matzen等人(2020)使用单目深度推断网络(第12.8节)来估计深度,从而可以从手机相机中的任何照片,甚至历史照片中生成3D照片,如图14.10c所示。当有历史立体照片时,可以利用这些照片创建更加精确的3D照片,如Luo、Kong等人(2020)所展示的那样。还可以通过单目深度推断从普通图像创建“3D肯·伯恩斯”效果,即小而迫近的视频片段(Niklaus、Mai等人2019)。
14.3 光场和光图
虽然基于图像的渲染方法可以从新的视角合成场景渲染,但它们提出了以下更一般的问题:
是否可以从所有可能的视角捕捉和呈现场景的外观,如果是的话,结果结构的复杂性是什么?
假设我们正在观察一个静态场景,即物体和照明设备固定不动,只有观察者在移动。在这种情况下,我们可以用虚拟摄像机的位置和方向(6个自由度)以及

图14.11 Lumigraph (Gortler,Grzeszczuk等,1996)©1996 ACM:(a)光线由其4D两平面参数(s,t)和(u,v)表示;(b)穿过3D光场子集(u,v,s)的切片。
它的内在属性(例如,焦距)。然而,如果我们捕捉每个可能的相机位置周围的二维球面图像,就可以根据这些信息重新渲染任何视图。因此,将三维空间中的相机位置与二维空间中的球面图像进行叉积运算,我们得到了阿德森和伯根(1991)提出的五维全景函数,这是麦克米伦和毕晓普基于图像的渲染系统的基础。
(1995).
请注意,当场景中没有光散射时,即没有烟雾或雾气,所有沿自由空间(固体或折射物体之间)的部分重合光线具有相同的颜色值。在这种情况下,我们可以将五维全光函数简化为所有可能光线的四维光场(Gortler,Grzeszczuk等,1996;Levoy和Hanrahan 1996;Levoy2006).10
为了简化这个四维函数的参数化,让我们在三维场景中放置两个大致包围感兴趣区域的平面,如图14.11a所示。任何终止于位于st平面前方的相机(假设该空间为空)的光线都会穿过这两个平面,在(s,t)和(u,v)处,并可以用其四维坐标(s,t,u,v)来描述。这个图示(及参数化)可以解释为描述了一组位于st平面上的相机,它们的像面是uv平面。uv平面可以置于无穷远,这相当于所有虚拟相机都朝向同一个方向。
在实际应用中,如果平面是有限范围的,可以使用有限光板L(s,t,u,v)生成相机通过(有限)视口在st平面上看到的任何合成视图,该视图的视锥体完全与远处的uv平面相交。为了使相机能够绕物体全方位移动,可以将围绕物体的三维空间分割成多个域,每个域都有自己的光板参数化。相反,如果相机在有界自由空间内向外移动,可以使用围绕相机的多个立方体面作为(s,t)平面。
思考四维空间是困难的,因此让我们将可视化降低一个维度。如果我们固定行值t,并限制相机沿s轴移动同时观察uv平面,我们可以将相机看到的所有稳定图像堆叠起来,以获得(u,v,s)极线体积,这在第12.7节中讨论过。穿过这个体积的“水平”横截面就是著名的极线平面图像(Bolles、Baker和Marimont 1987),即图14.11b所示的us切片。
正如你在这张切片中所见,每个彩色像素沿着一条线性轨迹移动,其斜率与其相对于uv平面的深度(视差)有关。(恰好位于uv平面上的像素看起来是“垂直”的,即它们不会随着相机沿s轴移动而移动。)此外,当相应的3D表面元素相互遮挡时,像素轨迹也会相互遮挡。然而,半透明像素则与背景像素合成(Section3.1.3(3.8)),而不是遮挡它们。因此,我们可以将相邻像素共享相似平面几何结构视为EPI条带或EPI管(Criminisi,Kang等,2005)。从缓慢穿过静态场景的相机拍摄的3D光场可以成为高精度3D重建的极佳来源,因为
Kim、Zimmer等人(2013)、Y cer、Kim等人(2016)在论文中证明了这一点
以及Sorkine-Hornung等人(2016)。
从虚拟相机中的像素(x,y)到对应的(s,t,u,v)坐标的方程相对容易推导,并在练习14.7中进行了概述。还可以证明,对于正交或透视相机而言,即那些在三维点与(x,y)像素之间存在线性投影关系的相机(2.63),其对应的像素集位于(s,t,u,v)光场中的二维超平面内(练习14.7)。
虽然光场可以用于从新颖的角度渲染复杂的3D场景,但如果已知其3D几何结构,可以获得更好的渲染效果(减少重影)。Gortler、Grzeszczuk等人(1996)的Lumigraph系统通过考虑每个3D光线对应的表面点的3D位置,扩展了基本的光场渲染方法。

图14.12 Lumigraph中的深度补偿(Gortler,Grzeszczuk等,1996)©1996 ACM。为了重新采样(s,u)虚线光线,根据平面外深度z修改每个离散的si相机位置对应的u参数,生成新的坐标u和u‘;在(u,s)光线空间中,原始样本(△)从(si,u)和(si-1,u)样本重新采样,这些样本本身是其相邻()样本的线性混合。
物体表面在距离uv平面z处。当我们向上查找相机si的像素颜色(假设光场是在一个规则的4D(s,t,u,v)网格上离散采样),实际的像素坐标是u,,而不是由(s,u)光线指定的原始u值。同样地,对于相机si+1(其中si≤s≤si+1),使用的是像素地址u,。因此,不是通过四线性插值最近的采样(s,t,u,v)值来确定给定光线的颜色,而是为每个离散的(si,ti)相机修改(u,v)值。
图14.12同样展示了射线空间中的相同推理。这里,原始连续值(s,u)射线用三角形表示,附近的采样离散值则以圆圈显示。与仅混合最近的四个样本不同,如垂直和水平虚线所示,修改后的(si,u)和(si+1,u)值被采样,并将其值进行混合。
生成的渲染系统产生的图像质量远优于无代理光场,当可以推断出三维几何形状时,这是首选方法。在后续研究中,Isaksen、McMillan和Gortler(2000)展示了如何使用场景的平面代理,即一个更简单的三维模型,来简化重采样方程。他们还描述了如何通过混合更近的样本(Levoy和Hanrahan 1996)来创建合成孔径照片,这些照片模仿了广角镜头可能看到的效果。类似的方法也可以用于重新聚焦用全光(微透镜阵列)相机(Ng、Levoy等2005;Ng 2005)或光场显微镜(Levoy、Ng等2006)拍摄的图像。此外,这种方法还可以用来穿透障碍物,使用极大的合成孔径聚焦于背景。
这可以模糊前景物体,使它们看起来半透明(Wilburn,Joshi等人,2005;Vaish,Szeliski等人,2006)。
既然我们已经了解了如何从光场中渲染新图像,那么如何捕捉这样的数据集呢?一种方法是使用运动控制装置或龙门架移动校准好的相机。另一种方法是手持拍摄照片,并通过校准台或运动结构法确定每张图像的姿态和内参校准。在这种情况下,图像需要重新分箱到一个常规的4D(s,t,u,v)空间中,才能用于渲染(Gortler,Grzeszczuk等,1996)。或者,可以直接使用原始图像,采用称为非结构化Lumigraph的过程,具体描述如下。
由于涉及的图像数量庞大,光场和光图可以非常难以存储和传输。幸运的是,正如你从图14.11b中可以看出的那样,光场中存在大量的冗余(相干性),通过首先计算一个三维模型,如光图所示,这种冗余可以更加明显地体现出来。已经开发出多种技术来压缩并逐步传输这些表示(Gortler,Grzeszczuk等,1996;Levoy和Hanrahan,1996;Rademacher和Bishop,1998;Magnor和Girod,2000;Wood,Azuma等,2000;Shum,Kang,和Chan,2003;Magnor,Ramanathan和Girod,2003;Zhang和Chen,2004;Shum,Chan,和Kang,2007)。
自20世纪90年代中期和21世纪初光场研究的初期以来,分析和渲染此类图像的技术不断进步。过去十年中的一些代表性论文和数据集包括Wanner和Goldluecke(2014年)、Honauer、Johannsen等人(2016年)、Kalantari、Wang和Ramamoorthi(2016年)、Wu、Masia等人(2017年)以及Shin、Jeon等人(2018年)。
当Lumigraph中的图像以非结构化(不规则)的方式获取时,将生成的光线重新采样到规则排列的(s,t,u,v)数据结构中可能会适得其反。这不仅因为重采样总会引入一定程度的混叠效应,还因为最终网格化的光场可能非常稀疏或不规则地分布。
另一种方法是直接从获取的图像中渲染,通过在虚拟摄像机中的每条光线找到原始图像中最接近的像素。Buehler、Bose等人(2001)提出的非结构化Lumigraph渲染(ULR)系统描述了如何选择这些像素。
通过结合多个保真度标准,包括极点一致性(光线到源相机中心的距离)、角度偏差(表面相似的入射方向)、分辨率(沿表面的采样密度)、连续性(与邻近像素)和一致性(沿光线)。这些标准可以结合起来确定每个虚拟相机像素与多个候选输入相机之间的权重函数,从中提取颜色。为了提高算法效率,计算过程是通过使用覆盖多面体对象网格模型的规则网格离散化虚拟相机的图像平面,并插值顶点之间的权重函数来完成的。
非结构化的Lumigraph在基于图像的渲染和光场渲染方面推广了先前的工作。当输入相机呈网格状时,ULR的行为与常规Lumigraph渲染相同。当可用的相机较少但几何形状准确时,算法的表现类似于视图依赖纹理映射(第14.1.1节)。如果有RGB-D深度图像,这些图像可以融合成低分辨率代理,在渲染时与高分辨率源图像结合(Hedman,Ritschel等,2016)。虽然最初的ULR论文使用手动构建的规则来确定像素权重,但也有可能通过深度神经网络学习这样的混合权重(Hedman,Philip等,2018;Riegler和Koltun,2020a)。
当然,使用二维参数化来表示光场并不是唯一的选择。(通常首先介绍的是这种方法,因为投影方程和可视化图最容易绘制和理解。)正如我们在讨论光场压缩时提到的,如果我们知道正在建模的物体或场景的三维形状,就可以有效地压缩光场,因为来自相邻表面元素的光线具有相似的颜色值。
事实上,如果物体完全扩散,忽略遮挡,这可以通过使用3D图形算法或z缓冲来处理,所有穿过给定表面点的光线都将具有相同的颜色值。因此,光场“坍缩”到通常定义在物体表面的二维纹理图上。相反,如果表面完全镜面反射(例如,镜子),每个表面点都会反射出该点周围环境的一个微小副本。在没有相互反射的情况下(例如,在大开放空间中的凸起物体),每个表面点只会反射远场环境图(Section2.2.1),这也是二维的。因此,重新参数化四维光场使其位于物体表面上似乎非常有益。
这些观测结果是伍德引入的表面光场表示的基础,

图14.13表面光场(Wood,Azuma等人,2000年)©2000 ACM:(a)一个具有强烈反射的高镜面物体的例子;(b)表面光场将从每个表面点发出的所有可见方向的光存储为“光球”。
Azuma等人(2000年)在他们的系统中,首先对所表示的对象建立精确的三维模型。然后估计或捕捉从每个表面点发出的所有光线的光球体(图14.13)。附近的光球体将高度相关,因此既适合压缩也适合操作。
为了估计每个光球的漫射成分,首先对每个通道的所有可见出射方向进行中值滤波。一旦从光球中减去这一部分,剩余的值主要由镜面成分构成,这些值围绕局部表面法线(2.90)反射,使每个光球成为该点周围局部环境的复制品。随后,可以使用预测编码、矢量量化或主成分分析来压缩附近的光球。
分解为漫射和镜面成分也可用于执行编辑或操作操作,例如重新绘制表面、改变反射的镜面成分(例如通过模糊或锐化镜面Lumispheres),甚至在保持详细表面外观的同时几何变形对象。
在最近的研究中,Park、Newcombe和Seitz(2018)使用RGB-D摄像头获取三维模型及其漫反射层,通过最小合成和迭代重新加权最小二乘法实现,具体讨论见第9.4.2节。然后,他们估计了一个简单的分段常数BRDF模型来考虑镜面成分。在后续的《在薯片袋中看世界》论文中,Park、Holynski和Seitz(2020)也估计了镜面反射图,这是环境图与物体镜面BRDF的卷积结果。关于估计空间变化的BRDF的其他技术,详见第13.7.1节。
总之,表面光场是为扫描的3D添加真实感的好方法
通过建模物体的镜面特性来避免这些模型在忽略反射时出现“纸板”(哑光)外观。对于较大的场景,特别是包含大型平面反射物如玻璃窗或光滑桌面的场景,可以将反射建模为单独的层,如第9.4.2节和第14.2.1节所述,或者作为真实的镜面表面(Whelan,Goesele等,2018),这可能更为合适。
一种有用且简单的光场渲染版本是带有视差的全景图像,即从某个旋转点前摆动的摄像机拍摄的视频或一系列照片。这样的全景图可以通过将摄像机安装在三脚架上的摇臂上来捕捉,或者更简单地,通过手持摄像机并围绕固定轴旋转身体来实现。
生成的图像集可以视为同心马赛克(Shum和He 1999;Shum、Wang等2002)或分层深度全景图(Zheng、Kang等2007)。术语“同心马赛克”源自一种特定的结构,该结构可用于重新组合所有采样的光线,实际上将每列像素与它所切向的同心圆的“半径”关联起来(Ishiguro、Yamamoto和Tsuji 1992;Shum和He 1999;Peleg、Ben-Ezra和Pritch 2001)。
从这些数据结构中渲染既快速又简单。如果我们假设场景足够远,对于任何虚拟摄像机位置,我们可以将虚拟摄像机中的每一列像素与输入图像集中的最近一列像素关联起来。(对于定期拍摄的图像集,此计算可以进行解析处理。)如果我们对这些像素的深度有大致了解,可以通过垂直拉伸列来补偿两台摄像机之间的深度变化。如果我们拥有更详细的深度图(Peleg,Ben-Ezra和Pritch2001;Li,Shum等2004;Zheng,Kang等2007),我们可以逐像素进行深度校正。
虽然虚拟摄像机的运动被限制在原始摄像机所在的平面内,并且在原始捕捉环的半径范围内,但由此产生的体验可以展示复杂的渲染现象,如反射和半透明效果,这些是无法通过纹理映射的三维模型来捕捉的。练习14.10要求你使用一系列手持照片或视频构建一个同心马赛克渲染系统。
虽然同心马赛克是通过沿(大致)圆形弧线移动相机来捕捉的,但也可以构建流形投影(Peleg和Herman 1997)、多中心投影图像(Rademacher和Bishop 1998)以及多视角全景图(Rom n、Garg和Levoy 2004;Rom n和Lensch 2006;Agarwala、Agrawala等2006;Kopf、Chen
等2010),我们在Section8.2.5中简要讨论过这些内容。
除了捕捉场景和物体的交互式查看外,光场渲染还可以用于为照片添加合成景深效果(Levoy2006)。在计算摄影章节(第10.3.2节)中,我们提到现代双镜头和/或双像素智能手机产生的深度估计可以用来合成模糊照片(Wadhwa,Garg等2018;Garg,Wadhwa等2019;Zhang,Wadhwa等2020)。
当有大量输入图像时,例如使用微透镜阵列时,可以将这些图像移动并组合以模拟大光圈镜头的效果,这被称为合成孔径摄影(Ng,Levoy等2005;Ng 2005),这是Lytro光场相机的基础。类似的想法已被用于光场显微镜中的浅景深(Levoy,Chen等2004;Levoy,Ng等2006),障碍物消除(Wilburn,Joshi等2005;Vaish,Szeliski等2006;Xue,Rubinstein等2015;Liu,Lai等2020a),以及编码孔径摄影(Levin,Fergus等2007;Zhou,Lin和Nayar 2009)。
14.4 环境问题
到目前为止,本章讨论了视图插值和光场,它们是用于从不同视角建模和渲染复杂静态场景的技术。
如果我们不围绕虚拟摄像机移动,而是取一个复杂的折射物体,比如图14.14中所示的水杯,并将其置于新的背景前会怎样?我们不再需要建模从场景发出的四维光线空间,而是需要建模这个物体视图中的每个像素如何折射来自其环境的入射光。
这种表示的内在维度是什么,我们如何捕捉它?假设我们将光线从像素(x;y)的相机追踪到物体上,光线以角度(φ;θ)反射或折射回其环境。如果我们假设其他物体和光源足够远(与我们在第14.3.2节中对表面光场所做的假设相同),那么这个4D映射(x;y)→(φ;θ)就捕捉到了折射物体与其环境之间的所有信息。Zongker、Werner等人(1999)称这种表示为环境遮罩,因为它不仅将对象遮罩过程(第10.4节)从一个图像复制到另一个图像,还考虑了物体与其环境之间微妙的折射或反射相互作用。
根据公式(3.8)和(10.29),前景物体可以表示为

图14.14环境背景:(a-b)将一个折射物体置于一系列背景前,其光图案将被正确折射(Zongker,Werner
(et al.1999) (c)可以使用高斯混合模型处理多次折射,(d)可以使用单个分级彩色背景提取实时马特(Chuang,Zongker et al.2000)©2000 ACM。
它预先乘以颜色和不透明度(αF,α)。然后可以将这种哑光合成到新的背景B上。
Ci = αiFi +(1 - αi)Bi (14.1)
其中i是待考虑的像素。在环境遮罩中,我们通过增加反射或折射项来建模环境与相机之间的间接光路径。在Zongker、Werner等人(1999)的原始工作中,这个间接成分Ii被建模为
Ii = Ri∫Ai (x)B(x)dx, (14.2)其中Ai是该像素的支持矩形区域,Ri是彩色反射率或透射率(对于彩色光泽表面或玻璃),B(x)是背景(环境)图像,在Ai (x)区域上进行积分。在后续研究中,Chuang、Zongker等人(2000)使用了定向高斯函数的叠加,
Rij ∫ Gij
其中每个二维高斯
Gij (x) = G2D (x; cij , σij , θij ) (14.4)
由其中心cij、未旋转宽度σij =(σ,σ)和方向θij建模。
给定一个环境背景的表示,我们如何为特定对象进行估计?诀窍是将对象放在显示器前(或被一组物体包围)。
(监视器),我们可以在其中改变照明模式B(x)并观察每个合成像素Ci的值。
与传统的双屏遮罩(第10.4.1节)一样,我们可以使用多种纯色背景来估计每个像素的前景颜色αiFi和部分覆盖(不透明度)αi。为了估计支持区域Ai在(14.2)中的面积,Zongker、Werner等人(1999年)使用了一系列不同频率和相位的周期性水平和垂直纯色条纹,这让人联想到用于非活动测距的结构光图案(第13.2节)。对于更复杂的高斯混合模型(14.3),Chuang、Zongker等人(2000年)在四个不同方向(水平、垂直和两条对角线)上扫描一系列窄高斯条纹,从而能够在每个像素处估计多个定向高斯响应。
一旦环境遮罩被“提取”后,只需用新图像B(x)替换背景,即可获得物体置于不同环境中的新合成图(图14.14a-c)。然而,在遮罩过程中使用多个背景,则无法适用于动态场景,例如水倒入玻璃杯(图14.14d)。在这种情况下,可以使用单个渐变色背景来估计每个像素的单个二维单色位移(Chuang,Zongker等,2000)。
正如前面讨论所指出的,环境遮罩原则上将每个像素(x,y)映射到光线的四维分布中,因此是一个六维表示。(实际上,每个二维像素的响应是通过十几个参数来参数化的,例如{F,α,B,R,A},而不是完整的映射。)如果我们想从每一个潜在视角来建模物体的折射特性怎么办?在这种情况下,我们需要从每条入射的四维光线到每条潜在出射的四维光线的映射,这是一个八维表示。如果我们使用与表面光场相同的技巧,可以通过其四维BRDF参数化每个表面点,从而将此映射回六维,但这会失去处理多条折射路径的能力。
如果要处理动态光场,我们需要增加另一个时间维度。(Wenger、Gardner等人(2005)给出了一个很好的动态外观和照明采集系统的例子。)同样地,如果需要连续的波长分布,这又会成为另一个维度。

图14.15基于图像的渲染中的几何-图像连续体(Kang、Szeliski和Anandan2000)©2000 IEEE。光谱左侧的表示使用更详细的几何和更简单的图像表示,而右侧的表示和算法使用更多的图像和更少的几何。
这些例子说明了通过采样来模拟视觉场景的全部复杂性可能极其昂贵。幸运的是,构建专门模型可以解决这些问题,这些模型利用了关于光传输物理知识以及现实物体的自然相干性。
本章研究的基于图像的渲染表示和算法涵盖了从经典的3D纹理贴图模型到纯采样光线基础表示(如光场,图14.15)的连续体。视图依赖纹理贴图和Lumigraph等表示仍然使用单一的全局几何模型,但选择从邻近图像中映射的颜色。视图依赖几何,例如多深度图,绕过了对连贯3D几何的需求,有时能更好地模拟局部非刚性效应,如镜面运动(Swaminathan,Kang等,2002;Criminisi,Kang等,2005)。具有深度和分层深度图像的精灵使用颜色和几何的基于图像的表示,并且可以通过变形操作而非3D几何光栅化高效地渲染。
最佳的表示和渲染算法的选择取决于输入图像的数量和质量以及预期的应用。当渲染邻近视图时,基于图像的表示能够捕捉到更多现实世界的视觉保真度,因为它们直接采样了其外观。另一方面,如果只有少数输入
图像可用或基于图像的模型需要进行操作,例如改变其形状或外观,更抽象的三维表示如几何模型和局部反射模型更为合适。随着我们继续捕捉和操作越来越多的视觉数据,这些方面关于基于图像的建模和渲染的研究将继续发展。
14.5 基于视频的渲染
由于可以使用多张图像来渲染新图像或交互体验,那么视频是否也能实现类似的效果呢?事实上,在基于视频的渲染和基于视频的动画领域已经做了相当多的工作。这两个术语最初由Sch dl、Szeliski等人(2000)提出,用于表示从捕获的视频片段生成
新的视频序列的过程。早期的一个例子是“视频重写”(Bregler、Covell和Slaney 1997),其中存档的视频片段通过让演员说出新的台词而被“重新动画化”(图14.16)。最近,一些研究人员使用“基于视频的渲染”这一术语来指代从工作室中放置的一组同步摄像机创建虚拟摄像机移动的过程(Magnor 2005)。(自由视角视频和3D视频这两个术语有时也被使用:见第14.5.4节。)
在本节中,我们介绍了一系列基于视频的渲染系统和应用。首先讨论的是基于视频的动画(第14.5.1节),其中视频片段被重新排列或修改,例如面部表情的捕捉与重渲染。这一类中的一个特例是视频纹理(第14.5.2节),源视频会被自动分割成段并重新循环播放,以创建无限长的视频动画。此外,还可以通过将静态图片或绘画分割成独立移动的区域,并使用随机运动场进行动画处理来创建此类动画(第14.5.3节)。
接下来,我们将注意力转向3D视频(第14.5.4节),在此过程中,多个同步的摄像机从不同方向拍摄场景。然后,可以使用基于图像的渲染技术,如视图插值,重新组合源视频帧,以创建源摄像机之间的虚拟路径,作为实时观看体验的一部分。最后,我们讨论通过全景摄像机驾驶或步行穿越环境来捕捉这些环境,从而创建交互式的视频漫游体验(第

图14.16视频重写(Bregler、Covell和Slaney1997)©1997 ACM:视频帧由与新音频轨道匹配的旧视频片段组成。
14.5.1基于视频的动画
正如我们上面提到的,基于视频的动画的一个早期例子是Video Rewrite,在这个例子中,原始视频片段中的帧被重新排列以匹配新的语音表达,例如用于电影配音(图14.16)。这在精神上类似于连接式语音合成系统的工作方式(Taylor2009)。
在他们的系统中,布雷格勒、科维尔和斯莱尼(1997)首先使用语音识别从源视频材料和新的音频流中提取音素。音素被组合成三音节(音素的三重组合),因为这能更好地模拟人们说话时的共发音效果。然后在源视频片段和音频轨道中找到匹配的三音节。选定的视频帧对应的嘴部图像随后被剪切并粘贴到需要重新动画或配音的视频片段中,同时进行适当的几何变换以补偿头部运动。在分析阶段,使用计算机视觉技术跟踪与嘴唇、下巴和头部相关的特征。在合成过程中,使用图像变形技术将相邻的嘴部形状融合成一个更加连贯的整体。在后续的研究中,埃扎特、盖格和波吉奥(2002)描述了如何利用多维可变形模型(Section13.6.2)结合正则化轨迹合成来改进这些结果。
一个更高级的版本,称为面部转移,使用新颖的源视频,而不仅仅是音频轨道,来驱动先前捕获视频的动画,即重新渲染带有适当视觉语言、表情和头部姿态元素的说话人视频(Vlasic,Brand等,2005)。这项工作是众多基于表演的动画系统之一(第7.1.6节),这些系统通常用于动画3D面部模型(图13.23–13.25)。虽然传统的基于表演的动画系统使用基于标记的动作捕捉(Williams 1990;Litwinowicz和Williams 1994;Ma,Jones等,2008),但现在可以直接使用视频片段来控制动画(Buck,Finkelstein等,2000;Pighin,Szeliski和Salesin,2002;Zhang,Snavely等,2004;Vlasic,Brand等。
al.2005;Roble和Zafar2009;Thies、Zollhofer等人2016;Thies、Zollh fer等人2018
;Zollh fer、Thies等人2018;Fried、Tewari等人2019;Egger、Smith等人2020;Tewari、Fried等人2020)。有关相关技术的更多详细信息,可参见第13.6.3节关于面部动画和第14.6节关于神经渲染。
除了最常用的面部动画应用外,基于视频的动画还可以应用于全身运动(第13.6.4节),例如通过匹配两个不同源视频之间的流场并使用其中一个来驱动另一个(Efros,Berg等2003;Wang,Liu等2018;Chan,Ginosar等2019)。另一种基于视频渲染的方法是使用流或3D建模将表面纹理解包成稳定的图像,然后可以对其进行操作并重新渲染到原始视频上(Pighin,Szeliski,和Salesin
14.5.2视频纹理
基于视频的动画是一种强大的手段,通过重新利用现有的视频片段来匹配其他所需活动或脚本,从而创建照片级真实的视频。如果我们不构建特殊的动画或叙事,而是希望视频以一种合理的方式继续播放会怎样?例如,许多网站使用图片或视频来突出其目的地,比如展示有冲浪和随风摇曳的棕榈树的美丽海滩。与其使用静态图像或在循环时出现不连续性的视频片段,我们能否将视频片段转换成一个无限长的动画,永远播放下去?
这个想法是视频纹理的基础,在视频纹理中,可以通过重新排列视频帧来任意扩展短视频片段,同时保持视觉连贯性(Sch dl,Szeliski等2000)。创建视频纹理的基本问题是
如何在不引入视觉伪影的情况下进行这种重新排列。你能想到如何做到这一点吗?
最简单的方法是通过视觉相似性(例如,L2距离)来匹配帧,并在看起来相似的帧之间跳转。不幸的是,如果两帧中的运动不同,就会产生明显的视觉伪影(视频会显得“卡顿”)。例如,如果我们未能匹配图14.17a中钟摆的运动,它可能会在摆动过程中突然改变方向。
我们如何将基本帧匹配扩展到运动匹配?原则上,我们可以在每一帧计算光流并进行匹配。然而,光流估计通常不可靠(尤其是在无纹理区域),而且如何权衡视觉和运动相似性之间的关系也不明确。作为替代方案,Sch dl、Szeliski等人(2000)建议匹配相邻视频帧的三元组或更大邻域,类似于video Rewrite匹配三音节词的方式。一
构建了所有视频帧之间的n×n相似度矩阵(其中n是帧的数量),一个简单的有限脉冲

图14.17视频纹理(Sch dl,Szeliski等2000)©2000 ACM:(a)一个时钟摆,运动方向正确匹配;(b)烛火,显示节奏-
(a)过渡弧;(c)旗帜通过跳跃时的变形生成;(d)篝火使用更长的交叉溶解效果;(e)瀑布同时交叉溶解多个序列;(f)微笑的动画脸;(g)两个摇摆的孩子分别进行动画处理;(h)气球自动分割成独立的移动区域;(i)由气泡、植物和鱼组成的合成鱼缸。这些图像对应的视频可以在https://www.cc.gatech.edu/gvu/perception/projects/videotexture.找到。
可以使用每个匹配序列的响应(FIR)过滤来强调匹配良好的子序列。
这场比赛计算的结果为我们提供了一个跳转表,或者等效地,是原始视频中任意两帧之间的转换概率。这在图14.17b中以红色弧线示意表示,其中红色条表示当前显示的是哪个视频帧,当进行前向或后向转换时,弧线会亮起。我们可以将这些转换概率视为编码了随机视频生成过程背后的隐马尔可夫模型(HMM)。
有时,在原始视频中无法找到完全匹配的子序列。在这种情况下,可以使用变形技术,即在转换期间扭曲和融合帧(第3.6.3节),以隐藏视觉差异(图14.17c)。如果运动足够混乱,如篝火或瀑布(图14.17d-ἧ),简单的融合(扩展交叉溶解)可能就足够了。通过在转换周围的时空体积上执行三维图割,也可以获得改进的过渡效果(Kwatra,Sch dl等,2003)。
视频纹理不必局限于火灾、风和水等混乱随机现象。令人愉悦的视频纹理可以由人创建,例如一张笑脸(如图14.17f所示)或在跑步机上跑步的人(Sch dl,Szeliski等,2000)。当多个物体或人物独立移动时,如图14.17
-17h所示,我们首先需要将视频分割成独立移动的区域,并分别对每个区域进行动画处理。此外,还可以通过缓慢平移的摄像机创建大型全景视频纹理(Agarwala,Zheng等,2005;He,Liao等,2017)。
视频纹理不仅能够以随机方式回放原始帧,还可以用于创建脚本化或交互式动画。如果我们提取单个元素,例如鱼缸中的鱼(图14.17i),并将其拆分为独立的视频精灵,我们就可以按照预设路径(通过匹配路径方向与原始精灵运动)来动画化这些元素,使我们的视频元素以期望的方式移动(Sch dl和Essa2002)。一个更近的例子是Vid2Player系统,该系统模拟网球运动员的动
和投篮,从而创建合成的视频真实游戏(张、斯库托等2021)。事实上,关于视频纹理的研究启发了从动作捕捉数据重新合成新运动序列的系统研究,有些人称之为“动作捕捉汤”(阿里坎和福赛思2002;科瓦尔、格莱彻和皮金2002;李、柴等2002;李、王和舒姆2002;普伦和布雷格勒2002)。
虽然视频纹理主要将视频分析为可以按时间重新排列的一系列帧(或区域),但时间纹理(Szummer和Picard1996;Bar-Joseph、El-Yaniv等2001)和动态纹理(Doretto、Chiuso等2003;Yuan、Wen等2004;Doretto和Soatto2006)将视频视为具有纹理的三维时空体。

图14.18动画化静态图片(Chuang,Goldman等,2005)©2005 ACM。(a)输入的静态图像被手动分割成(b)多个层次。(c)每个层次随后使用不同的随机运动纹理进行动画处理(d)动画化的层次再合成以生成(e)最终的动画
属性,可以使用自回归时间模型进行描述,并结合分层表示(Chan和Vasconcelos 2009)。在最近的研究中,视频纹理创作系统得到了扩展,允许控制不同区域的动态性(运动量)(Joshi、Mehta等2012;Liao、Joshi和Hoppe 2013;Yan、Liu和Furukawa 2017;He、Liao等2017;Oh、Joo等2017),并改进了循环过渡(Liao、Finch和Hoppe 2015)。
虽然视频纹理可以将一个短视频片段变成无限长的视频,但同样的事情能否用单个静态图像实现呢?答案是肯定的,只要你愿意先将图像分割成不同的层,然后分别对每一层进行动画处理。
创、高盛等人(2005)描述了如何使用交互式遮罩技术将图像分解为独立的图层。每个图层随后通过特定类别的合成运动进行动画处理。如图14.18所示,船来回摇晃,树木随风摆动,云水平移动,水面泛起涟漪,这些效果都通过形状噪声位移图实现。所有这些效果都可以与一些全局控制参数关联,例如虚拟风的速度和方向。经过单独动画处理后,各图层可以合成以创建最终的动态渲染。
在最近的研究中,Holynski、Curless等人(2021)训练了一个深度网络来拍摄一张静态照片,产生一个合理的运动场,并将图像编码为深度多分辨率特征-
然后使用欧拉运动双向地在时间上输送这些特征,采用受Niklaus和Liu(2020)以及Wiles、Gkioxari等人(2020)启发的架构。生成的深度特征随后被解码,以产生带有合成随机流体运动的循环视频片段。
在过去十年里,3D电影已经成为一种成熟的媒介。目前,这类影片使用立体摄像机拍摄,并在影院(或家中)通过佩戴偏振眼镜的观众观看。然而,在未来,家庭观众可能希望使用多区域自动立体显示设备观看这些电影,每个人都能获得自己定制的立体影像流,并可以在场景中移动,从不同角度观看。
计算机视觉领域开发的立体匹配技术以及图形学中的基于图像的渲染(视图插值)技术,在这些场景中都是必不可少的组成部分,这些场景有时被称为自由视角视频(Carranza,Theobalt等,2003)或虚拟视角视频(Zitnick,Kang等,2004)。除了解决一系列逐帧重建和视图插值问题外,分析阶段生成的深度图或近似图必须在时间上保持一致,以避免闪烁伪影。神经渲染技术(Tewari,Fried等,2020,第6.3节)也可用于重建和渲染阶段。
舒姆、陈和康(2007)以及马格诺(2005)对各种视频视图插值技术和系统进行了很好的概述。这些技术包括卡纳德、兰德和纳拉亚南(1997)的虚拟现实系统,以及韦杜达、贝克和卡纳德(2005)的沉浸式视频,莫齐、卡特克雷等人(1996)的基于图像的视觉壳体,马图西克、布勒等人(2000;马图西克、布勒和麦克米伦2001)的基于图像的视觉壳体,以及卡兰萨、西奥巴尔特等人(2003)的自由视角视频,所有这些都使用全局3D几何模型(基于表面(第13.3节)或体积(第13.5节))作为渲染的代理。韦杜达、贝克和卡纳德(2005)的工作还计算了场景流,即对应表面元素之间的3D运动,这可以用于多视角视频流的空间时间插值。更近期的场景流变体是尼梅耶、梅舍德尔等人(2019)的占用流研究。
Zitnick、Kang等人(2004)的虚拟视角视频系统则为每张输入图像关联了一个两层深度图,这使得他们能够准确建模诸如物体边界处出现的混合像素等遮挡效果。他们的系统由八个同步连接到磁盘阵列的摄像机组成(图14.19a),首先使用基于分割的立体技术为每张输入图像提取深度图。

图14.19视频视图插值(Zitnick,Kang等,2004)©2004 ACM:(a)捕获硬件由八个同步摄像机组成;(b)每个摄像机的背景和前景图像在融合前进行渲染和合成;(c)边界抠像前后的两层表示;(d)背景颜色估计;(e)背景深度估计;(f)前景颜色估计。
(图14.19e)。在物体边界附近(深度不连续处),背景层沿前景物体后方的条带延伸(图14.19c),其颜色从未被遮挡的相邻图像中估计(图14.19d)。然后使用自动抠像技术(第10.4节)来估计前景层边界像素的透明度和颜色比例(图14.19f)。
在渲染时,给定一个新的虚拟摄像机位于两个原始摄像机之间,相邻摄像机中的图层被渲染为纹理贴图三角形,前景层(可能具有分数不透明度)随后叠加到背景层上(图14.19b)。生成的两张图像通过比较各自的z缓冲区值进行合并和混合。(当两个z值足够接近时,计算两种颜色的线性混合。)交互式渲染系统使用常规图形硬件实时运行。因此,可以在播放视频时改变观察者的视角,或冻结场景以在三维中探索它。Rogmans、Lu等人(2009)随后开发了GPU实现的实时立体匹配和实时渲染算法,使他们能够在实时环境中探索算法替代方案。
使用离线立体匹配从八个立体相机计算出的深度图已被用于3D视频压缩的研究(Smolic和Kauff2005;Gotchev和Rosenhahn2009;Tech、Chen等人2015)。主动视频速率深度传感相机,如我们在第13.2.1节讨论的3DV Zcam(Iddan和Yahav2001),是另一种
当有大量间距很近的摄像机可用时,如斯坦福光场摄像机(Wilburn,Joshi等人,2005年),可能并不总是需要计算显式的深度图来创建基于视频的渲染效果,尽管如果这样做的话,结果通常会更好(Vaish,Szeliski等人,2006年)。
近年来,3D视频研究迎来了复兴,部分原因是虚拟现实头盔的普及,这些设备可以提供强烈的沉浸感来观看此类视频。谷歌的Jump虚拟现实捕捉系统(Anderson,Gallup等,2016)使用16个GoPro相机排列在一个直径28厘米的环上,捕捉多段视频,然后离线拼接成一对全向立体(ODS)视频(Ishiguro,Yamamoto,和Tsuji,1992;Peleg,Ben-Ezra,和Pritch,2001;Richardt,Pritch等,2013),在观看时可以进行扭曲处理,生成每只眼睛的独立图像。Cabral(2016)在同一时期也介绍了一种类似的系统,该系统由紧密同步的工业视觉相机构建。
正如安德森、加尔普等人(2016)所指出的,然而,ODS表示在交互式观看方面存在严重局限,例如不支持头部倾斜、平移运动,或在上下看时无法生成正确的深度。最近由塞拉诺、金等人(2019)、帕拉·波佐、托克斯维格等人(2019)以及布罗克顿、弗林等人(2020)开发的系统支持完整的六自由度(6DoF)视频,这使得观众可以在限定体积内移动,同时为每只眼睛生成透视正确的图像。然而,这些系统需要在离线构建阶段进行多视图立体匹配,以生成支持此类观看所需的三维代理。
虽然这些系统旨在捕捉内外体验,用户可以观看周围展开的视频,但将摄像头指向外部则可用于捕捉一个或多个演员表演活动(Kanade,Rander,和Narayanan 1997;Joo,Liu等2015;Tang,Dou等2018)。这类设置通常被称为自由视角视频或体积表演捕捉系统。最近版本的此类系统使用深度网络来重建、表示、压缩和/或渲染随时间演变的体积场景(Martin-Brualla,Pandey等2018;Pandey,Tkach等2019;Lombardi,Simon等2019;Tang,Singh等2020;Peng,Zhang等2021),正如Tewari,Fried等人(2020,第6.3节)最近关于神经渲染的综述所总结的那样。尽管大多数这些系统需要定制的多摄像头设备,也可以从手持视频集合(Bansal,Vo等2020)甚至单个移动中构建3D视频。
智能手机摄像头(Yoon,Kim等人,2020;Luo,Huang等人,2020)。
视频摄像机阵列能够从多个视角同时捕捉3D动态场景,从而让观众能够从接近原始拍摄位置的视角探索场景。如果我们希望捕捉一个扩展区域,比如一个家庭、一个电影布景,甚至是一个整个城市呢?
在这种情况下,将摄像机移动到环境中并以交互式视频漫游的形式回放视频更为合理。为了使观众能够全方位地观察周围环境,最好使用全景摄像机(Uyttendaele,Criminisi等,2004)。
一种结构化获取过程的方法是在二维水平平面上捕捉这些图像,例如,在房间内叠加的网格上。由此产生的图像海洋(Aliaga,Funkhouser等,2003)可用于实现捕获位置之间的连续运动。然而,将这一想法扩展到更大的场景中,例如超出单个房间,可能会变得繁琐且数据密集。
相反,探索空间的一种自然方式通常是沿着预先设定的路径行走,就像博物馆或家庭导览带领用户沿着特定路径前进一样,比如穿过每个房间的中央。同样地,城市级别的探索可以通过驾车行驶在每条街道的中央,并允许用户在每个交叉口分支来实现。这一想法可以追溯到阿斯彭电影地图项目(Lippman1980),该项目将从移动车辆拍摄的模拟视频记录到光盘上,以便后续的互动播放。
视频技术的进步使得使用小型共址摄像机阵列捕捉全景(球形)视频成为可能,例如乌特恩代尔、克里米尼西等人(2004)为他们的交互式视频漫游项目开发的Point Grey Ladybug相机(图ure14.20b)。在他们的系统中,来自六个摄像机的同步视频流(图14.20a)通过专门为此项目开发的各种技术拼接成360°全景图。
因为相机没有共享相同的投影中心,相机之间的视差会导致重叠视野中的重影(图14.20c)。为了消除这种现象,使用多视角平面扫描立体算法来估计重叠区域中每一列的每个像素深度。为了校准相机之间的相对位置,相机在原地旋转,并使用约束结构运动算法(图11.15)来

图14.20基于视频的演练(Uyttendaele,Criminisi等,2004)©2004 IEEE:
(a)视频预处理系统图;(b)点灰女士相机;(c)使用多视角平面扫描去除鬼影;(d)点跟踪,用于校准和稳定;(e)交互式花园导览,附带下方地图;(f)高空地图制作及声音定位;(g)交互式家庭导览,顶部有导航栏,底部有兴趣图标。
估计相对相机姿态和内参。然后对行走视频进行特征跟踪,以稳定视频序列。刘、格莱彻等人(2009年)、科普夫、科恩和斯泽利斯基(2014年)以及科普夫(2016年)最近也开展了类似的研究。
室内环境中的窗户以及阳光充足的户外环境中的强阴影,通常具有超出视频传感器能力的动态范围。因此,瓢虫相机具备可编程曝光功能,能够在后续视频帧中进行曝光补偿。为了将这些视频帧合并成高动态范围(HDR)视频,在合并前需要对相邻帧的像素进行运动补偿(Kang,Uyttendaele等,2003)。
互动导览体验会变得更加丰富和易于导航,如果能提供一张概览地图作为体验的一部分。在Figure14.20f中,地图上有注释,可以在游览过程中显示,还有本地化的音源,当观众靠近时会播放(音量不同)。视频序列与地图的对齐过程可以使用一种称为地图关联的技术来自动化(Levin和Szeliski 2004)。
所有这些元素结合在一起,为用户提供丰富、互动且沉浸式的体验。图14.20e展示了一次贝尔维尤植物园的漫步,下方的实时视频窗口中有一张透视概览地图。地面上的箭头用于指示可能的行进方向。观众只需将视线对准其中一个箭头(该体验可以使用游戏控制器驱动),然后沿着所选路径“行走”前进。
图14.20g展示了一次室内家庭游览体验。除了左下角的示意图和顶部导航栏上的相邻房间名称外,每当主窗口中出现感兴趣的项目,如房主的艺术品时,底部会出现图标。点击这些图标可以获取更多信息和3D视图。
互动视频导览的发展激发了人们对基于360°视频的虚拟旅行和地图体验的新兴趣,这从谷歌街景和360城市等商业网站中可见一斑。同样的视频还可以用于生成逐向驾驶路线,利用扩展视野和图像渲染技术来提升体验(陈、纽伯特等人,2009)。
虽然最初,360°相机显得既奇特又昂贵,但近年来它们已广泛成为消费产品,例如2013年首次推出的热门RICOH THETA相机和GoPro MAX运动相机。拍摄360°视频时,可以使用专为此类视频设计的算法(Kopf2016)或基于相机IMU读数的专有算法来稳定视频。尽管大多数这些相机只能生成单目照片和视频,但VR180相机拥有两个镜头,因此能够创建

图14.21第一人称超时延视频创建(Kopf,Cohen,和Szeliski2014)©2014 ACM:(a) 3D摄像机路径和点云恢复,随后进行平滑路径规划;(b)每个相机的3D代理估计;(c)使用MRF和泊松混合选择源帧和接缝。
宽视场立体内容。甚至可以通过仔细拼接和转换两个360°摄像机流来生成3D 360°内容(Matzen,Cohen等人,2017)。
除了捕捉风景名胜和热门活动的沉浸式照片和视频外,360°和普通运动相机还可以佩戴、在环境中移动,然后加速创建超时延视频(Kopf,Cohen,和Szeliski 2014)。由于这些视频在大幅加速时可能会出现大量的平移运动和视差,因此仅仅补偿相机旋转或甚至扭曲单个输入帧是不够的,因为大量的补偿运动可能会迫使虚拟摄像机超出视频帧。相反,在构建稀疏的三维模型并平滑相机路径后,选择关键帧,并通过插值稀疏的三维点云计算每个关键帧的三维代理,如图14.21所示。然后使用马尔可夫随机场进行拼接和扭曲(采用泊松混合),以确保尽可能平滑和视觉连续性。该系统结合了许多先前开发的三维建模、计算摄影和基于图像的渲染算法,生成大规模环境(如城市)和活动(如攀岩和滑雪)的非常流畅的高速游览。
随着我们不断捕捉越来越多的真实世界影像和视频,本章中描述的交互式建模、探索和渲染技术将在将虚拟体验带入世界偏远地区以及让每个人更贴近地重温特别记忆方面发挥更大的作用。
14.6 神经渲染
基于图像的渲染的最新发展是将深度神经网络引入到基于图像的渲染的建模(构建)和查看部分
管道。神经渲染已应用于多个不同领域,包括风格和纹理处理以及二维语义光合作用(第5.5.4节和第10.5.3节)、三维物体形状和外观建模(第13.5.1节)、面部动画和重现(第13.6.3节)、三维身体捕捉和重放(第13.6.4节)、新颖视角合成(第14.1节)、自由视角视频(第14.5.4节)以及重新照明(Duch ne,Riant等,2015;Meka,Haene等,2019;Philip,Gharbi等,2019;Sun,Barron等,2019
;Zhou,Hadap等,2019;Zhang,Barron等,2020)。
Tewari、Fried等人(2020)的最新报告中对所有这些应用和技术进行了全面调查,其摘要指出:
神经渲染是一个新兴且迅速发展的领域,它将生成式机器学习技术与计算机图形学中的物理知识相结合,例如通过将可微渲染集成到网络训练中。神经渲染在计算机图形和视觉领域有着广泛的应用前景,有望成为图形学界的一个新领域...
调查包含超过230篇参考文献,重点介绍了46篇代表性论文,分为六个主要类别,即语义光合作用、新颖视角合成、自由视角视频、重照明、面部重现和身体重现。正如您所见,这些类别与前一段提到的书中章节有所重叠。基于此内容的一系列讲座可以在CVPR教程中找到(Tewari,Zollh fer等,2020),并且TUM AI客座讲座系列中的几场讲座也涉及神经渲染研究。Bemana、Myszkowski等人(2020,表1)的X-Field
论文还列出了相关空间、时间和光照插值论文的精彩表格,重点在于深度方法,而Dellaert和Yen- Chen(2021)的简短书目则总结了更近期的技术。一些神经渲染系统是通过可微渲染实现的,Kato、Beker等人(2020)对此进行了综述。
正如我们在前面提到的许多神经渲染技术中已经看到的,这里我们将重点放在这些技术在基于图像的三维建模和渲染中的应用。近年来,神经渲染的研究成果可以归类为几种主要方式。在本节中,我选择使用四种广泛研究的三维表示方法,即:纹理贴图网格、深度图像和层次、体素网格以及隐式函数
纹理贴图网格。如第13章所述,三角形网格是建模和渲染3D场景的一种方便的表示方法,可以从以下内容中重建:

图14.22神经图像渲染示例:(a)深度扭曲源图像的深度融合(Hedman,Philip等,2018)©2018 ACM;(b)在野外可控视角和光照条件下的神经重渲染(Meshry,Goldman等,2019)©2019 IEEE;(c)使用深度MPI进行全景光函数的众包采样(Li,Xian等,2020)©2020斯普林格。(d) SynSin:从单张图像生成新视角(Wiles,Gkioxari等,2020)©2020 IEEE。
使用多视角立体图像。最早将神经网络用于3D渲染过程的论文之一是Hedman、Philip等人(2018)提出的深度融合系统,他们通过一个深度神经网络增强了一个非结构化的Lumigraph渲染管道(Buehler、Bosse等人,2001),该神经网络计算每个新视角选择的扭曲图像的逐像素混合权重,如图14.22a所示。LookinGood (Martin-Brualla、Pandey等人,2018)采用单张或多张纹理映射的3D上身或全身渲染,并填补空洞,去噪外观,使用在保留视图上训练的U-Net提高分辨率。同样地,深度学习超级采样(DLSS)利用GPU硬件实现的编码器-解码器DNN实时提高渲染游戏的分辨率(Burnes,2020)。
虽然这些系统会扭曲彩色纹理或图像(即视图依赖纹理),然后应用神经网络后处理,也可以先将图像转换为“神经”编码,再进行扭曲和混合。自由视图合成(Riegler和Koltun 2020a)首先使用多视角立体构建新视图的局部3D模型。然后将源图像编码为神经代码,重新投影到新视角,并使用循环神经网络和softmax进行合成。与在渲染时扭曲神经代码后再混合和解码不同,后续的稳定视图合成系统(Riegler和Koltun 2020b)从每个表面点的所有入射光线收集神经代码,然后通过表面聚合网络将其组合,生成沿光线到达新视图相机的输出神经代码。延迟神经渲染(Thies、Zollh fer和Nießner2019)利用三维表面上的(u;v)参数化来学习和存储神经代码的二维纹理图,这些代码可以在渲染时采样和解码。
深度图像和层次。为了处理在不同时间和天气条件下拍摄的图像,即“野外”拍摄的图像,Meshry、Goldman等人(2019)使用DNN为每个输入图像及其相关的深度图像(通过传统多视图立体计算)计算一个潜在的“外观”向量,如图14.22b所示。在渲染时,可以调整外观(除了3D视角外),以探索图像拍摄条件的变化范围。Li、Xian等人(2020)开发了一个相关的流程(图14.22c),该流程不是存储单一的“深度”颜色/深度/外观图像或缓冲区,而是使用多平面图像(MPI)。与之前的系统一样,使用编码器-解码器调制外观向量(采用自适应实例归一化)来渲染最终图像,在这种情况下是通过中间的MPI进行视图变形和叠加合成。与使用许多平行精细切片平面不同,GeLaTO(生成性潜在纹理对象)系统使用少量定向平面(“广告牌”)及其关联的神经纹理。
用于建模薄透明物体,如眼镜(Martin-Brualla,Pandey等,2020)。在渲染时,这些纹理会被扭曲,然后使用U-Net解码并合成,生成最终的RGBA粒子。
虽然所有这些先前的系统都使用多张图像来构建三维神经表示,但SynSin(单图像合成)(Wiles,Gkioxari等,2020)仅从一张彩色图像开始,利用DNN将该图像转化为神经特征F和深度D缓冲区对,如图14.22d所示。在渲染时,根据其关联的深度和相机视图矩阵,神经特征被软权重平铺,并从前向后合成以获得神经渲染帧F,然后解码为最终的颜色新视图IG。在语义视图合成中,Huang,Tseng等(2020)从一个语义标签图开始,使用语义图像合成(第5.5.4节)将其转换为合成的彩色图像和深度图。这些图像随后用于创建一个多平面图像,从中可以渲染出新的视图。Holynski,Curless等(2021)训练了一个深度网络,以静态照片为基础,幻觉出合理的运动场,将图像编码为具有软混合权重的深层特征,这些特征在时间上双向传播,并解码渲染的神经特征帧,生成带有合成随机流体运动的循环视频片段,如第14.5.3节所述。
体素表示。另一种可用于神经渲染的三维表示是三维体素网格。图14.23展示了两篇论文中的建模和渲染流程。DeepVoxels (Sitzmann,Thies等,2019)学习给定三维对象的神经代码的三维嵌入。在渲染时,这些嵌入被投影到二维视图中,通过遮挡网络过滤(类似于从后向前的透明度合成),然后解码成最终图像。neural Volumes (Lombardi,Simon等,2019)使用编码器-解码器将一组多视角彩色图像转换为三维RGBα体积及其相关的体积变形场,可以模拟面部表情的变化。在渲染时,颜色体积被变形,然后使用光线行进法生成最终的二维RGBα前景图像。17在最近的研究中,Weng,Curless和Kemelmacher-Shlizerman(2020)展示了如何从单目视频中构建和动画化可变形的神经体积,例如运动员的动作
基于坐标神经表示。本节讨论的最终表示是使用全连接网络实现的隐式函数,现在这些网络更加

图14.23体素网格神经渲染示例:(a) DeepVoxels (Sitzmann,Thies等人,2019)©2019 IEEE;(b) Neural Volumes (Lombardi,Simon等人,2019)©2019 ACM。
通常称为多层感知器或MLP。我们已经在第13.5.1节中讨论了[0;1]占用率和隐式有符号距离函数在三维形状建模中的应用,其中提到了诸如occupancy Networks (Mescheder,Oechsle等,2019)、IM-NET (Chen和Zhang,2019)、DeepSDF (Park,Florence等,2019)以及Convolutional occupancy Networks (Peng,Niemeyer等,2020)等论文。
为了渲染彩色图像,这些表示还需要编码表面或整个体积的外观(例如颜色、纹理或光场)信息。纹理场(Oechsle,Mescheder等,2019)训练一个基于三维形状和潜在外观(例如汽车颜色)的MLP,以生成可以用于纹理映射3D模型的3D体色彩场,如图14.24a所示。这种表示可以通过微分渲染扩展,直接计算深度梯度,如微分体渲染(DVR)(Niemeyer,Mescheder等,2020)。像素对齐隐式函数(PIFu)网络(Saito,Huang等,2019;Saito,Simon等,2020)也使用MLP来计算
正如Jon Barron和其他人所指出的,只有签名的距离函数才能将“隐式函数”编码为其体积值的水平集。更广泛的技术类别,包括不透明度模型,通常被称为坐标回归网络或基于坐标的多层感知机。

图14.24隐式函数(MLP)神经渲染示例:(a)纹理场(Oechsle,Mescheder等,2019)©2019 IEEE;(b)神经辐射场(Mildenhall,Srinivasan等,2020)©2020 Springer。
体积内外和颜色场的计算,以及仅从单张彩色图像中生成完整的3D模型的能力,如图13.18所示。场景表示网络(Sitzmann、Zollh fer和Wetzstein2019)使用MLP将体积(x;y;z)坐标映射到高维神经
特征,这些特征被用于光线行进LSTM(基于3D视图并输出像素坐标)和1×1颜色像素解码器来生成最终图像。该网络可以插值外观和形状潜在变量。
一个有趣的混合系统是王等人(2021)提出的IBRNet系统,该系统用即时多视角立体匹配和基于图像的渲染替换了训练好的逐对象MLP。与其他体素神经渲染方法一样,网络通过沿光线行进并在每个采样位置计算密度和神经外观特征来评估新视角图像中的每条光线。然而,它不是从预训练的MLP中查找这些值,而是从少量相邻输入图像中采样神经特征,
类似于《非结构化光片》(Buehler,Bosse等,2001;Hedman,Philip等,2018)和《稳定视图合成》(Riegler和Koltun,2020b),这些方法使用预计算的3D表面模型(而IBRNet不使用)。沿光线的不透明度和外观值通过变压器架构进行细化,该架构取代了立体匹配器中传统的胜者通吃模块,随后是对颜色和密度的经典体绘制。
为了模拟视点依赖效应,如塑料物体上的高光效果,即建模完整的光照场(第14.3节),神经辐射场(NeRF)扩展了从(x,y,z)空间位置到包括观察方向(θ,φ)作为输入的隐式映射,如图14.24b所示(Mildenhall,Srinivasan等,2020)。每个(x,y,z)查询首先转换为由八度频率的正弦波组成的位姿编码,然后进入一个256通道的MLP。这些位姿编码还被注入第五层,而观察方向的编码则在第九层注入,这是计算不透明度的地方(Mildenhall,Srinivasan等,2020,图7)。事实证明,这些位姿编码对于使MLP能够表示细微细节至关重要,这一点在Tancik,Srinivasan等(2020)以及Sitzmann,Martel等(2020)的siren(正弦表示网络)论文中得到了更深入的探讨,该论文使用周期性的(正弦)激活函数。
也可以预先训练这些神经网络,即使用元学习,在更广泛的对象类别上加速新图像的优化任务(Sitzmann,Chan等2020;Tancik,Mildenhall等2021),同时结合锥追踪和集成位置编码来减少混叠并处理多分辨率输入和输出(Bar- ron,Mildenhall等2021)。张、Riegler等人(2020)的NeRF++论文通过增加“由内向外”的1/r反向球参数化,扩展了原始的NeRF表示以处理无界3D场景,而神经稀疏体素场则在每个非空单元中构建一个带有隐式神经函数的八叉树(Liu,Gu等2020)。
不是建模不透明度,Yariv、Kasten等人(2020)开发的隐式可微渲染器(IDR)建模了一个带符号的距离函数,这使得他们在渲染时能够提取具有解析法线的水平集表面,这些法线随后传递给神经渲染器,后者建模视点依赖效果。该系统还使用可微渲染自动调整输入相机位置。神经光片渲染利用正弦表示网络生成更紧凑的表示(Kellnhofer、Jebe等人,2021)。它们还可以导出一个3D网格,以实现更快的视点依赖光片渲染。Takikawa、Litalien等人(2021)也构建了隐式带符号距离场,但他们没有使用单一的MLP,而是构建了一个稀疏八叉树结构,该结构在单元格中存储神经特征(类似于神经稀疏体素场),并支持细节层次和快速球体。
追踪。神经隐式曲面(NeuS)也使用带符号距离表示法,但使用了更好的处理表面遮挡的渲染公式(Wang,Liu等,2021)。
虽然NeRF、IDR和NSVF需要大量静态物体在受控(均匀光照)条件下拍摄的图像,但NeRF in the Wild (Martin-Brualla,Radwan等,2021)则从一个地标旅游地点获取一组无结构的图像,不仅能够建模天气和时间变化等外观变化,还能移除如游客等短暂遮挡物。NeRF也可以通过单张或少量图像构建,例如在像素级NeRF (Yu,Ye等,2020)中,通过将特定类别的神经辐射场与这些输入条件化来实现。可变形的神经辐射场或“nerfies”(Park,Sinha等,2020)、神经场景流场(Li,Niklaus等,2021)、动态神经辐射场(Pumarola,Corona等,2021)、时空神经辐照场(Xian,Huang等,2021)以及HyperNeRF (Park,Sinha等,2021)均以手持视频作为输入,这些视频围绕一个人拍摄或在场景中移动。它们不仅建模视角变化,还建模体积非刚性变形,如头部或身体运动及表情变化,要么使用学习到的变形场,要么增加时间作为额外的输入变量,或者将表示嵌入更高维度。
还可以将神经反射场(NeRF)扩展到不仅建模三维坐标中的不透明度和视图依赖的颜色,还建模它们与潜在光源的相互作用。神经反射和可见性场(NeRV)通过为每个查询的三维坐标返回表面法线、参数化BRDF以及该点处出射光线的环境可见性和预期终止深度来实现这一点(Srinivasan,Deng等,2021)。神经反射分解(NeRD)使用隐式MLP建模密度和颜色,并返回一个外观向量,该向量被解码为参数化BRDF(Boss,Braun等,2020)。然后,它利用环境光照,用球面高斯近似,结合密度法线和BRDF,在该体素处渲染最终的颜色样本。PhySG采用类似的方法,使用带符号的距离场表示形状,使用球面高斯混合表示BRDF (Zhang,Luan等,2021)。
大多数包含视图依赖效果的神经渲染技术在渲染时速度较慢,因为它们需要沿每条光线采样体积空间,并使用昂贵的多层感知器来执行每个位置/方向查找。为了在建模视图依赖效果的同时实现实时渲染,近期的一些论文采用了高效的空间数据结构(如八叉树、稀疏网格或多平面图像)来存储不透明度和基础颜色(或潜在的小型多层感知器),然后利用辐射场的分解近似来建模视图依赖效果(Wizadwongsa,Phongthawee等,2021;Garbin,Kowalski等,2021;Reiser,Peng等,2021;Yu,Li等,2021;Hedman,Srinivasan等,2021)。尽管这些论文中各阶段所使用的表示方法的具体细节有所不同,
它们都始于与原始NeRF论文或其扩展相关的高保真视图依赖模型,然后“烘焙”或“提炼”这些模型,以生成更快评估的空间数据结构和简化的(但仍然准确的)视图依赖模型。最终系统产生的高保真渲染效果与完整的神经辐射场相同,而运行速度通常比纯MLP表示快1000倍。
正如本节简要讨论所示,神经渲染是一个极其活跃的研究领域,每隔几个月就会提出新的架构(Dellaert和Yen-Chen 2021)。要了解最新进展的最佳途径,就像计算机视觉领域的其他主题一样,是查看arXiv和领先的计算机视觉、图形学及机器学习会议。
14.7 附加阅读材料
关于基于图像的渲染,康、李等人(2006)和舒姆、陈、康(2007)进行了两项优秀的综述研究。更早的综述可参见康(1999)、麦克米伦和戈特勒(1999)以及德贝韦克(1999)。如今,这一领域常被称为新颖视图合成(NVS),最近在CVPR上发表的一篇教程(加洛、特罗科利等人,2020)对历史和当前技术进行了很好的概述。
基于图像的渲染这一术语由麦克米伦和毕晓普(1995)提出,尽管该领域的开创性论文是陈和威廉姆斯(1993)关于视图插值的研究。德贝韦克、泰勒和马利克(1996)描述了他们的Fac¸ade系统,不仅创建了多种基于图像的建模工具,还引入了广泛使用的视图依赖纹理映射技术。早期关于平面替身和层次的工作由谢德、利辛斯基等人(1996)、伦吉尔和斯奈德(1997)以及托尔博格和卡吉亚(1996)完成,而基于精灵并带有深度的新工作则由谢德、戈特勒等人(1998)描述。使用大量具有RGBA颜色和透明度的平行平面(最初由斯泽利斯基和戈兰德(1999)称为“醋酸盐堆栈”模型)被周、塔克等人(2018)重新发现,现在被称为多平面图像(MPI)。这种表示方法在最近的3D捕捉和渲染管道中广泛使用(米尔登霍尔、斯里尼瓦桑等人2019;崔、加洛等人2019;布罗克顿、弗林等人2020;阿塔尔、林等人2020;林、徐等人2020)。为了准确建模反射,MPI中使用的alpha合成操作需要替换为加法模型,如辛哈、科普夫等人(2012)和科普夫、朗古斯等人(2013)所述。
基于图像的渲染的两篇基础论文是Levoy和Hanrahan(1996)的光场渲染和Gortler、Grzeszczuk等人(1996)的Lumigraph。Buehler、Bose等人(2001)将Lumigraph方法推广到不规则分布的集合.
图像,而莱沃伊(2006)则提供了光场和基于图像的渲染主题的综述及较为温和的介绍。吴、马西亚等人(2017)提供了这一主题的最新综述。最近,神经渲染技术被用于改进无结构光图中使用的混合启发式方法(赫德曼、菲利普等人,2018;里格勒和科尔图恩,2020a)。
表面光场(Wood,Azuma等,2000;Park,Newcombe和Seitz,2018;Yariv,Kasten等,2020)为具有精确已知表面几何的光场提供了替代参数化方法,支持更好的压缩和编辑表面属性的可能性。同心马赛克(Shum和He,1999;Shum,Wang等,2002)和带有深度的全景图(Peleg,Ben-Ezra和Pritch,2001;Li,Shum等,2004;Zheng,Kang等,2007)为使用平移相机捕捉的光场提供了有用的参数化方法。多视角图像(Rademacher和Bishop,1998)和流形投影(Peleg和Herman,1997),虽然不是真正的光场,但与这些概念密切相关。
在光场向更高维结构扩展的可能方法中,环境贴图(Zongker,Werner等人,1999;Chuang,Zongker等人,2000)是最有用的,特别是用于将捕获的对象放入新场景。
基于视频的渲染,即利用视频重新创建新的动画或虚拟体验,始于Szummer和Picard(1996)、Bregler、Covell和Slaney(1997)以及Sch dl、Szeliski等人(2000)的开创性工作。这些基本重定向方法的重要
后续研究包括Sch dl和Essa(2002)、Kwatra、Sch dl等人(2003)、Doretto、Chiuso等人(
2003)、Wang和Zhu(2003
)、Zhong和Sclaroff(2003)、Yuan、Wen等人(2004)、Doretto和Soatto(2006)、Zhao和Pietikinen(2007)、Chan和Vasconcelos(2009)、Joshi
、Mehta等人(2012)、Liao、Joshi和Hoppe(2013)、Liao、Finch和Hoppe(2015)、Yan、Liu和Furukawa(2017)、He、Liao等人(2017)以及Oh、Joo等人(2017)。相关技术也被用于性能驱动的视频动画(Zollh fer、Thies等人2018;Fried、Tewari等人2019;Chan、Ginosar
等人2019;Egger、Smith等人2020)。
允许用户根据多个同步视频流改变其3D视角的系统包括Moezzi、Katkere等人(1996)、Kanade、Rander和Narayanan(1997)、Matusik、Buehler等人(2000)、Matusik、Buehler和McMillan(2001)、Carranza、Theobalt等人(2003)、Zitnick、Kang等人(2004)、Magnor(2005)、Vedula、Baker和Kanade(2005)、Joo、Liu等人(2015)、Anderson、Gallup等人(2016)、Tang、Dou等人(2018)、Serrano、Kim等人(2019)、Parra Pozo、Toksvig等人(2019)、Bansal、Vo等人(2020)、Broxton、Flynn等人(2020)和Tewari、Fried等人(2020)。3D(多视角)视频编码和压缩也是研究的活跃领域(Smolic和Kauff2005;Gotchev和Rosenhahn2009),并用于3D蓝光光盘和多视角视频编码(MVC)扩展到高
高效视频编码(HEVC)标准(Tech,Chen等人,2015)。
整个神经渲染领域是相当新的,最初的出版物集中在
二维图像合成(Zhu,Kr henb hl等,2016
;Isola,Zhu等,2017)和更多
最近,该技术被应用于三维新视图合成(Hedman,Philip等,2018;Martin-Brualla,Pandey等,2018)。Tewari,Fried等(2020)提供了这一领域的优秀综述,包含230篇参考文献和46篇重点论文。其他概述包括CVPR关于神经渲染的教程(Tewari,Zollh等,2020),TUM AI客座讲座
系列中的几场演讲,Bemana,Myszkowski等(2020,表1)的X-Fields论文,以及Dellaert和Yen-Chen(2021)最近的书目。
14.8 练习
例14.1:深度图像渲染。开发一个“视图外推”算法,重新渲染先前计算的立体深度图及其对应的参考颜色图像。
1.使用一个3D图形网格渲染系统,例如OpenGL,每个像素四边形包含两个三角形,并且采用透视(投影)纹理映射(Debevec、Yu和Borshukov,1998)。
2.或者,使用在Exercise3.24中构建的单次或两次前向变形器,并使用(2.68–2.70)将其扩展为从视差或深度转换为位移。
3.(可选)在视图插值或外推过程中引入的直线上的扭结在视觉上是明显的,这是图像变形系统允许您指定线对应关系的原因之一(Beier和Neely1992)。修改您的深度估计算法以匹配和估计直线的几何形状,并将其纳入
示例14.2:查看插值。扩展您在上一个练习中创建的系统,以渲染两个参考视图,然后使用z缓冲区、孔填充和混合(变形)组合来混合图像,以创建最终图像(第14.1节)。
1.(可选)如果两个源图像的曝光度差异很大,那么填充孔洞的区域和混合区域的曝光度也会不同。您能否扩展您的算法来缓解这种情况?
2.(可选)扩展算法,以在相邻视图之间执行三向(三线性)插值。您可以三角化参考摄像机姿态,并使用虚拟摄像机的重心坐标来确定混合权重。
Ex 14.3:查看变形。修改视图插值算法,以在非刚性对象的视图之间执行变形,例如一个人改变表情。
1.不使用纯立体算法,而是使用一般流算法来计算位移,但将其分为由于摄像机运动引起的刚性位移和非刚性变形。
2.在渲染时,使用刚性几何体确定新的像素位置,但同时添加非刚性位移的一部分。
3.(可选)取一张图片,例如《蒙娜丽莎》或朋友的照片,并创建一个动画的三维视图变形(Seitz和Dyer1996)。
(a)在图像中找到垂直对称轴,并反射你的参考图像,以提供一个虚拟的对(假设人的发型是有点对称的)。
(b)利用运动结构来确定这对相机的相对姿态。
(c)使用密集立体匹配来估计三维形状。
示例14.4:查看依赖纹理映射。使用您创建的3D模型以及原始图像来实现一个依赖于视图的纹理映射系统。
1.使用在练习11.10、12.9、12.10或13.8中开发的三维重建技术之一,从多张照片构建基于三维图像的三角化模型。
2.从你的照片中提取每个模型脸的纹理,要么通过执行适当的重采样,要么弄清楚如何使用纹理映射软件直接访问源图像。
3.对于每个新的摄像机视图,选择每个可见模型面的最佳源图像。
4.将此扩展到混合前两三个纹理。这比较棘手,因为它涉及到纹理混合或像素着色(Debevec、Taylor和Malik 1996;Debevec、Yu和Borshukov 1998;Pighin、Hecker等1998)。
例14.5:分层深度图像。扩展你的视图插值算法(练习14.2),以存储每个像素多个深度或颜色值(Shade,Gortler等,1998),即分层深度图像(LDI)。相应地修改渲染算法。对于数据,你可以使用合成光线追踪、分层重建模型或体素重建。
例14.6:从精灵或图层渲染。扩展您的视图插值算法以处理多个平面或精灵(第14.2.1节)(Shade,Gortler等人,1998年)。
1.使用在练习9.7中开发的技术提取图层。
2.或者,使用交互式绘画和三维定位系统提取您的平面图(Kang1998;Oh,Chen等2001;Shum,Sun等2004)。
3.根据预期的可见性确定从后到前的顺序,或者在渲染算法中添加z缓冲区以处理遮挡。
4.渲染并合成所有生成的图层,可选地使用alpha矩阵处理图层和精灵的边缘。
5.尝试一种较新的多平面图像(MPI)技术(Zhou,Tucker等人,2018)。
例14.7:光场变换。推导出将常规图像与四维光场坐标联系起来的方程。
1.确定远平面(u,v)坐标与虚拟摄像机(x,y)坐标之间的映射。
(a)首先,根据其(u,v)坐标参数化uv平面上的三维点。
(b)使用常用的3×4相机矩阵P(2.63),将生成的3D点投影到相机像素(x,y,1)。
(c)推导出与(u,v)和(x,y)坐标相关的二维同构。
2.写出一个类似的变换,将(s,t)坐标转换为(x,y)坐标。
3.证明如果虚拟摄像机实际上位于(s,t)平面上,那么(s,t)值仅取决于摄像机的图像中心,并且与(x,y)无关。
4.证明由常规正射或透视相机拍摄的图像,即在三维点和(x,y)像素之间具有线性投影关系的相机(2.63),采样
沿二维超平面的(s,t,u,v)光场。
Ex 14.8:光场和Lumigraph渲染。实现一个光场或Lumigraph渲染系统:
1.从http://lightfield.stanford.edu或https://lightfield-analysis.uni-konstanz.de下载一个光场数据集。
2.编写一个算法,使用四线性插值法(s、t、u、v)射线样本合成新的视图。
3.尝试改变与您想要的视图相对应的焦平面(Isaksen、McMillan和Gortler2000),看看生成的图像是否更清晰。
4.为场景中的对象确定一个三维代理。您可以通过对其中一个光场运行多视图立体来获得每个图像的深度图。
5.实现Lumigraph渲染算法,该算法根据每个表面元素的三维位置修改光线采样。
6.自己收集一组图像,并使用结构运动来确定它们的姿态。
7.实现Buehler、Bose等人(2001)提出的非结构化Lumigraph渲染算法。
例14.9:表面光场。构建一个表面光场(Wood,Azuma等人,2000年),并观察你能够将其压缩到什么程度。
1.获取一个有趣的镜面场景或物体的光场,或者从http://lightfield.stanford.edu或https://lightfield-analysis.uni-konstanz.de下载一个。
2.使用多视立体算法构建物体的三维模型,该算法对由于镜面反射而产生的异常值具有鲁棒性。
3.估计对象上每个表面点的光球。
4.估计其漫射分量。中值是最佳方法吗?为什么不使用最小颜色值?如果漫射分量上有朗伯阴影会发生什么?
5.使用Wood、Azuma等人(2000)建议的技术之一对Lumisphere的剩余部分进行建模和压缩,或者发明你自己的技术。
6.研究压缩算法的工作效果和产生的伪影。
7.(可选)开发一个系统来编辑和操作你的表面光场。
例14.10:手持同心马赛克。开发一个系统来导航手持同心马赛克。
站在房间中间,把摄像机伸直放在你面前,然后转圈。
2.使用运动结构系统确定每个输入帧的相机姿态和稀疏3D结构。
3.(可选)将图像像素重新组合成更规则的同心马赛克结构。
4.在查看时,根据新相机的视图(应该接近原始拍摄的平面)确定要显示的源像素。您可以简化计算以确定每个输出列的源列(和缩放)。
5.(可选)使用稀疏的三维结构,插值到密集深度图,以改善渲染效果(Zheng,Kang等人,2007)。
Ex 14.11:视频纹理。拍摄一些自然现象的视频,如喷泉、火焰或笑脸,并将视频无缝循环成无限长度的视频(Sch dl,Szeliski等,2000)。
1.使用L2(平方差之和)比较原始片段中的所有帧
度量。(这假设视频是在三脚架上拍摄的,或者已经稳定了。)
2.按时间筛选比较表,以突出匹配良好的时间子序列。
3.通过一些指数分布将相似性表转换为跳跃概率表。务必修改接近末尾的转换,以免在最后一帧中“卡住”。
4.从第一帧开始,使用过渡表来决定是向前跳、向后跳还是继续到下一帧。
5.(可选)将其他扩展添加到原始视频纹理概念中,例如多个移动区域、交互式控制或图割时空纹理接缝。
Ex 14.12:神经渲染。最近的大多数神经渲染论文都附带开源代码以及精心获取的数据集。
尝试下载多个这样的文件,并在不同的数据集上运行不同的算法。比较你获得的渲染质量,并列出你检测到的视觉伪影以及如何改进它们。
如果可行,尝试捕获您自己的数据集,并描述当前算法的其他断点。
Chapter 15 Conclusion
在这本书中,我们涵盖了广泛的计算机视觉主题。我们首先回顾了基础几何学和光学,以及图像和信号处理、连续和离散优化、统计建模和机器学习等数学工具。然后,我们利用这些知识开发了计算机视觉算法,如图像增强和分割、物体检测与分类、运动估计和三维形状重建。这些组件反过来又使我们能够构建更复杂的应用程序,例如大规模图像检索、将图像转换为描述、将多张图像拼接成更宽广和更高动态范围的合成图、跟踪人物和物体、在新环境中导航,以及通过嵌入式3D覆盖增强视频。
自本书第一版出版以来的十年间,计算机视觉领域取得了迅猛发展,不仅在视觉算法的成熟度和可靠性方面有所提升,从业者数量和商业应用也大幅增加。最显著的进步在于深度学习,它现在能够实现远超十年前水平的视觉识别性能。深度学习还广泛应用于基础视觉算法中,如图像增强、运动估计和三维形状恢复。其他进展包括可靠的实时跟踪和重建,使得自主导航和基于手机的增强现实等应用成为可能。而复杂的图像处理技术的进步,则催生了计算摄影算法,这些算法运行在每一部移动电话上,产生的图像质量超过了昂贵的传统摄影设备所能提供的。
你可能会问:为什么我们的领域如此广泛,难道没有可以用来简化我们研究的统一原则吗?部分答案在于计算机视觉的广泛定义,即使用图像捕捉、分析和解释我们的三维环境。
以及视频,还有视觉图像形成中固有的惊人复杂性。在某些方面,我们的领域与汽车工程学一样复杂,后者需要了解内燃机、机械、空气动力学、人体工程学、电路和控制系统等众多主题。计算机视觉同样借鉴了广泛的相关学科,这使得在一学期课程中涵盖所有内容变得困难,甚至在研究生学习期间掌握这些知识也颇具挑战。相反,计算机视觉惊人的广度和技术复杂性正是吸引许多人投身这一研究领域的原因。
由于这种丰富性和在制作和衡量进步方面的困难,我试图在我的学生中,希望在这本书的读者中,灌输一种基于工程、科学、统计学和机器学习原则的学科。
工程解决问题的方法是首先仔细定义要解决的整体问题,并质疑这一过程中固有的基本假设和目标。完成这些后,会实施并仔细测试多种替代方案或方法,关注诸如可靠性和计算成本等问题。最后,在实际环境中部署并评估一个或多个解决方案。因此,本书包含了不同的视觉问题解决方案,许多方案在练习中进行了概述,供学生自行实现和测试。
科学方法建立在对物理原理的基本理解之上。对于计算机视觉而言,这包括自然和人工结构的物理学、图像形成,包括光照和大气效应、光学以及噪声传感器。任务是使用稳定且高效的算法来逆向处理这些信息,以获得场景和其他感兴趣量的可靠描述。科学方法还鼓励我们提出并检验假设,这与工程学科中固有的广泛测试和评估相似。
因为图像形成过程本身存在许多不确定性和模糊性,通常需要采用统计方法来建模这些不确定性、先验分布以及图像形成过程中的退化。贝叶斯推断技术可以用来结合先验模型和测量模型,估计未知参数并建模其不确定性。高效的学习和推理算法,如动态规划、图割和信念传播,在这一过程中往往发挥着关键作用。
最后,机器学习技术在大量训练数据的驱动下——包括有标签(监督)和无标签(非监督)的数据——使得开发能够发现世界中难以描述的规律和模式的模型成为可能,这可以提高推理的可靠性。然而,尽管学习技术带来了惊人的进步,我们
必须对基于学习的方法的固有限制保持谨慎,而不仅仅是因为“训练数据不足或有偏见”而把问题推给别人。
沿着这些思路,我受到了Shree Nayar的在线讲座系列《计算机视觉的基本原理》中一段内容的启发:1
由于深度学习如今非常流行,你可能会想,了解视觉的基本原理是否值得,或者更广泛地说,了解任何领域的基本原理是否值得。对于一个任务,为什么不直接用大量数据训练神经网络来解决这个任务呢?
确实,在某些应用中,这种方法可能已经足够。但有几个理由让我们坚持基础。首先,训练网络去学习可以用第一原理精确简洁地描述的现象是既费力又不必要的。其次,当网络表现不佳时,第一原理是你唯一能理解其原因的方法。第三,收集数据来训练网络可能会很繁琐,有时甚至不切实际。在这种情况下,基于第一原理的模型可以用来合成数据,而不是收集数据。最后,学习任何领域第一原理最令人信服的原因是好奇心。人类的独特之处在于这种天生的好奇心,即想知道事物为何如此运作。
鉴于本书所涵盖的广泛材料,未来我们可能会看到哪些新的发展?从过去十年中机器学习的巨大进步来看,显而易见的是,包括优化连续标准和指标的能力在内的架构和算法微调能力将继续发展并带来显著改进。目前,前馈卷积架构占据主导地位,主要使用加权线性求和和简单的非线性函数,但很可能会演变为包含注意力机制和自上而下反馈等更复杂架构,正如我们已经开始看到的那样。复杂的专用成像传感器可能会越来越多地被使用,取代并增强最初为摄影开发的可见光成像传感器的使用。与额外传感器(如IMU)以及可能的主动感知(在电力允许的情况下)的集成,将使实时定位和三维重建等经典问题更加可靠和普遍。
计算机视觉最具挑战性的应用可能仍将在人工通用智能(AGI)领域,其目标是创建表现出相同特征的系统
在人工智能的许多其他方面取得进展,看看这些不同的AI模式和能力如何相互利用以提高性能将是一件有趣的事情。
无论这些研究努力的结果如何,计算机视觉已经在许多领域产生了巨大影响,包括数字摄影、视觉效果、医学成像、安全与监控、图像搜索、产品推荐以及视障人士辅助。该领域的广泛问题和技术,结合数学的丰富性和由此产生的算法的实用性,将确保这一领域在未来多年内仍是一个令人兴奋的研究方向。
