地理空间视角下的 SIR 传染病模型模拟与可视化

在当今世界，传染病的传播模拟已成为公共卫生领域的重要研究工具。传统的传染病模型往往忽略了空间因素，将整个群体视为一个均质的整体。然而，现实中的疾病传播与地理空间位置密切相关，相邻区域之间的传播风险远高于远距离区域。今天，我们将通过一个结合地理信息系统 (GIS) 和随机模拟算法的案例，深入探讨如何在空间维度上模拟传染病的传播过程。

引言：当传染病模型遇上地理空间

传染病的传播从来都不是抽象的数字游戏，它实实在在地发生在我们生活的城市空间中。想象一下，在伦敦这样的大都市中，不同区域之间的人口流动、空间邻近性如何影响疾病的传播速度和范围？这正是我们今天要探索的主题。

我们将使用经典的 SIR 传染病模型，但会为其添加 "地理空间" 这一重要维度。SIR 模型将人群分为三类：易感者 (Susceptible)、感染者 (Infectious) 和康复者 (Recovered)。通过引入空间权重矩阵，我们可以量化不同区域之间的邻近关系，使模型能够更真实地反映疾病在地理空间上的传播过程。

数据准备：加载伦敦的地理空间数据

首先，我们需要准备地理空间数据。代码中加载了伦敦市 (City of London) 和卡姆登区 (Camden) 的低级统计区 (LSOA) 边界数据。这些数据是英国国家统计数据的一部分，能够帮助我们精确界定不同的地理单元。

# 加载伦敦市和卡姆登区的shapefile
lon = gpd.read_file("LSOA_2011_BFE_City_of_London.shp")
cam = gpd.read_file("LSOA_2011_BFE_Camden.shp")
# 合并两个GeoDataFrame
df = pd.concat([lon, cam], ignore_index=True)

地理数据通常有不同的坐标参考系统 (CRS)。为了确保后续计算的准确性，我们需要进行坐标转换。我们先保留一个 WGS84 (经纬度) 坐标系的副本用于地图绘制，然后将数据转换为等距坐标系 (EPSG:3857) 用于质心计算和距离测量。 

# 保留WGS84副本用于绘制经纬度地图
df_ll = df.to_crs(epsg=4326)# 在进行质心计算前重新投影到等距CRS(EPSG:3857)
df = df_ll.to_crs(epsg=3857)

坐标系统的转换是地理空间分析中非常关键的一步。想象一下，如果我们在经纬度坐标系中直接计算两点之间的距离，由于地球曲率的影响，结果会有很大误差。而转换到等距坐标系后，我们就可以像在平面上一样准确计算距离和面积了 📐。

 

接下来，我们计算每个区域的质心，并获取它们在两种坐标系中的坐标：

# 计算两种CRS下的质心
centroids_3857 = df.geometry.centroid
coords_3857 = np.vstack([centroids_3857.x, centroids_3857.y]).T
centroids_ll = df_ll.geometry.centroid
coords_ll = np.vstack([centroids_ll.x, centroids_ll.y]).T

空间权重矩阵：定义区域间的邻近关系

在空间分析中，"邻近性" 是一个关键概念。如何定义两个区域是否相邻？在代码中，我们使用了 "Queen contiguity" 规则，这是空间统计中常用的一种邻近性定义。Queen contiguity 认为，如果两个区域共享一条边或一个角，则它们是相邻的。

# 使用Queen邻接构建空间权重
w = libpysal.weights.Queen.from_dataframe(df, use_index=True)# 转换为权重矩阵
n = len(df)
W = np.zeros((n, n), dtype=int)
for i, neighbors in w.neighbors.items():for j in neighbors:W[i, j] = 1W[j, i] = 1  # 对称矩阵

这种邻接关系定义很有意思，它模拟了一种 "棋盘式" 的邻近性。想象一下国际象棋中的皇后可以沿对角线移动，Queen contiguity 就是用这种方式定义邻近性的 � chess。与只考虑共享边的 "Rook contiguity" 相比，它考虑了更多的邻近关系。

为了更直观地理解我们构建的权重矩阵，我们可以绘制权重分布的直方图：

# 正权重的直方图
dist = W[W > 0]
plt.figure()
plt.hist(dist, bins=20)
plt.title('Distribution of Weights > 0')
plt.show()

由于我们使用的是二元邻接矩阵 (相邻为 1，不相邻为 0)，这个直方图应该会呈现出明显的双峰分布，其中大部分权重为 0，而相邻区域的权重为 1。不过，在后续步骤中，我们还会引入阈值处理，让邻接关系变得更加 "模糊"。

构建空间网络：阈值化邻接关系

有时候，我们可能需要考虑更灵活的邻近关系定义。例如，不仅考虑直接相邻的区域，还可以根据距离或其他因素定义一个 "影响范围"。在代码中，我们通过设置一个阈值，将权重矩阵转换为一个二元邻接矩阵：

# 阈值邻接
threshold = 0.16
adj = (W > threshold).astype(int)

这里的阈值设置是一个关键参数，它决定了哪些区域会被视为 "相邻"。阈值越高，邻接关系越严格，网络中的连接越少；阈值越低，邻接关系越宽松，网络中的连接越多。这个参数的设置需要根据具体问题和数据特点来调整 🧩。

我们可以将这些邻接关系可视化，看看在地理空间上区域之间是如何连接的：

# 绘制高于阈值的边
g_df = df_ll.copy()
plt.figure(figsize=(6, 6))
g_df.plot(facecolor='none', edgecolor='gray')
plt.scatter(coords_ll[:, 0], coords_ll[:, 1], s=10, color='black')
for i in range(n):for j in range(i + 1, n):if adj[i, j]:plt.plot([coords_ll[i, 0], coords_ll[j, 0]],[coords_ll[i, 1], coords_ll[j, 1]],color='blue', linewidth=0.5)
plt.title('Network Edges (thresholded)')
plt.show()

 

看着这些蓝色的连接线在地图上延伸，我们仿佛看到了疾病可能传播的 "高速公路"。这些连接线构成了一个空间网络，疾病将在这个网络上进行传播 🌐。

SIR 模型：从经典到空间扩展

现在，我们来介绍 SIR 模型的基本原理。SIR 模型是一个经典的传染病模型，它将人群分为三个状态：

• S (Susceptible): 易感者，尚未感染但可能被感染的人
• I (Infectious): 感染者，具有传染性的人
• R (Recovered): 康复者，已经康复并获得免疫力的人

模型的核心是两个速率参数：

• β(beta): 感染率，表示易感者与感染者接触后被感染的概率
• γ(gamma): 康复率，表示感染者康复的概率

在传统的 SIR 模型中，通常假设人群是完全混合的，即每个人与其他人接触的概率是相等的。但在我们的空间扩展版本中，这个假设被打破了。我们考虑了空间邻近性，即一个区域的感染状态会受到其相邻区域感染状态的影响。

在代码中，我们设置了感染率和康复率参数：

# SIR参数
beta = 3.0  # 感染率
gamma = 1.0  # 康复率

这些参数的值会显著影响疾病传播的动态。例如，较高的感染率会导致疾病更快地传播，而较高的康复率会缩短感染期，减缓疾病的传播速度 ⚙️。

初始状态设置：疫情的起点

每个传染病模拟都需要一个起点。在代码中，我们随机选择一个区域作为初始感染区域：

# 初始化状态: 'S', 'I', 'R'
status = np.array(['S'] * n)
i0 = random.randrange(n)
status[i0] = 'I'

这个初始感染点的选择虽然是随机的，但在现实中，疫情的起点可能与人口密度、交通枢纽等因素有关。如果我们有更详细的数据，我们可以根据实际情况选择更合理的初始感染点 🦠。

Gillespie 随机模拟算法：捕捉传染病的随机性

传染病的传播本质上是一个随机过程，因为每个接触事件是否导致感染都是概率性的。为了准确捕捉这种随机性，我们使用了 Gillespie 随机模拟算法，这是一种在分子尺度上模拟随机过程的强大方法。

Gillespie 算法的核心思想是：

1. 计算系统中所有可能事件的发生速率
2. 根据这些速率计算每个事件发生的概率
3. 随机选择一个事件发生
4. 计算到下一个事件发生的时间间隔
5. 重复上述过程

在我们的 SIR 模型中，有两种可能的事件：

1. 感染事件：易感者被感染者感染
2. 康复事件：感染者康复

让我们看看代码中是如何实现这个算法的：

# 存储模拟结果
T_max = 10.0  # 最大模拟时间
times = [0.0]  # 时间点列表
states = [status.copy()]  # 每个时间点的状态列表
adj_list = {i: list(np.where(adj[i] == 1)[0]) for i in range(n)}  # 邻接列表
current_time = 0.0  # 当前时间# Gillespie模拟
i = 0
while current_time < T_max:# 找出所有感染者I_indices = np.where(status == 'I')[0]# 计算每个感染者的康复速率rec_rates = {idx: gamma for idx in I_indices}# 找出所有易感者S_indices = np.where(status == 'S')[0]# 计算每个易感者的感染速率，与相邻感染者数量有关inf_rates = {idx: beta * sum(status[j] == 'I' for j in adj_list[idx]) for idx in S_indices}# 合并所有事件及其速率all_rates = {**rec_rates, **inf_rates}total_rate = sum(all_rates.values())# 如果没有事件发生，结束模拟if total_rate <= 0:break# 提取事件节点和速率nodes, rates = zip(*all_rates.items())# 计算每个事件发生的概率probs = np.array(rates) / total_rate# 随机选择一个事件event_node = np.random.choice(nodes, p=probs)# 更新状态if status[event_node] == 'S':status[event_node] = 'I'  # 易感者被感染else:status[event_node] = 'R'  # 感染者康复# 计算到下一个事件的时间间隔dt = np.random.exponential(1.0 / total_rate)current_time += dt# 存储当前时间和状态times.append(current_time)states.append(status.copy())i += 1

Gillespie 算法的一个重要特点是它精确地模拟了随机过程的时间演化，而不是像欧拉法那样使用固定的时间步长。这使得它在处理具有不同时间尺度的事件时特别有效 ⏳。

在我们的实现中，每个易感者的感染速率不仅取决于感染率 β，还取决于其相邻区域中有多少个感染区域。这正是空间因素被引入模型的关键所在 🌍。

结果分析：传染病的时间动态

模拟结束后，我们可以分析传染病在时间上的传播动态。首先，我们创建一个时间序列数据框，记录每个时间点上易感者、感染者和康复者的数量：

# 时间序列DataFrame
df_counts = [{'time': t,'S': int((st == 'S').sum()),'I': int((st == 'I').sum()),'R': int((st == 'R').sum())}for t, st in zip(times, states)]
df_ts = pd.DataFrame(df_counts)

然后，我们可以绘制这三类人群随时间变化的曲线： 

plt.figure()
for compartment in ['S', 'I', 'R']:plt.plot(df_ts['time'], df_ts[compartment], label=compartment)
plt.xlabel('Time')
plt.ylabel('Count')
plt.legend()
plt.title('SIR Dynamics Over Time')
plt.show()

 

典型的 SIR 模型时间曲线应该呈现出这样的模式：

• 易感者数量 (S) 随时间单调递减
• 感染者数量 (I) 先增加后减少，形成一个峰值
• 康复者数量 (R) 随时间单调递增

看着这些曲线的变化，我们可以直观地理解传染病的传播过程：从少数人感染开始，逐渐扩散到高峰，然后随着越来越多的人康复，感染人数逐渐减少 📈📉。

空间传播动画：疾病在地理空间上的扩散

最令人兴奋的部分莫过于将疾病的空间传播过程可视化。通过创建动画，我们可以直观地看到疾病如何从初始感染点开始，沿着空间网络向周围区域扩散。

首先，我们准备动画所需的数据：

# 准备DataFrame用于动画
records = []
for step, st in enumerate(states):for idx, s in enumerate(st):records.append({'time_step': step,'node': idx,'status': s,'x': coords_ll[idx, 0],'y': coords_ll[idx, 1]})
anim_df = pd.DataFrame(records)

然后，我们实现动画生成函数： 

# 使用PillowWriter生成动画
def animate_sir_map(output_file='london.gif', fps=5):fig, ax = plt.subplots(figsize=(6, 6))def update(frame):ax.clear()df_ll.plot(ax=ax, facecolor='lightgray', edgecolor='white')df_step = anim_df[anim_df['time_step'] == frame]for label, color in zip(['S', 'I', 'R'], ['blue', 'red', 'green']):sub = df_step[df_step['status'] == label]ax.scatter(sub['x'], sub['y'], label=label, s=20)ax.set_title(f"Time step: {frame}")ax.legend(loc='upper right', fontsize='small')ax.set_axis_off()writer = PillowWriter(fps=fps)anim = FuncAnimation(fig, update, frames=len(states), interval=200)anim.save(output_file, writer=writer)print(f"Animation saved as {output_file} using PillowWriter")# 生成动画
animate_sir_map()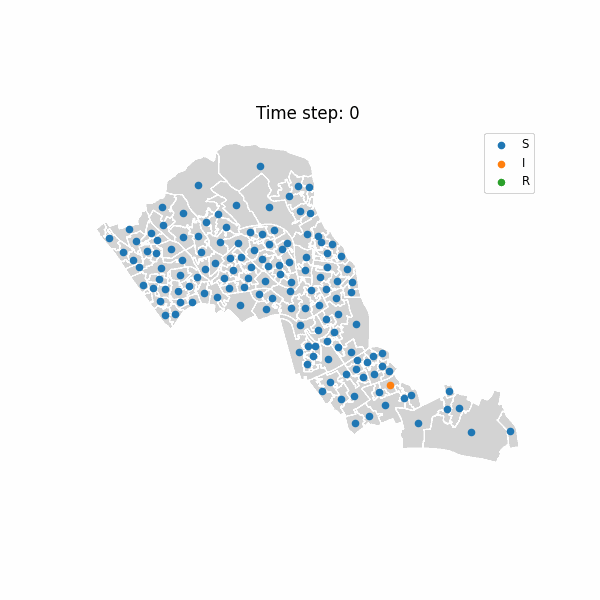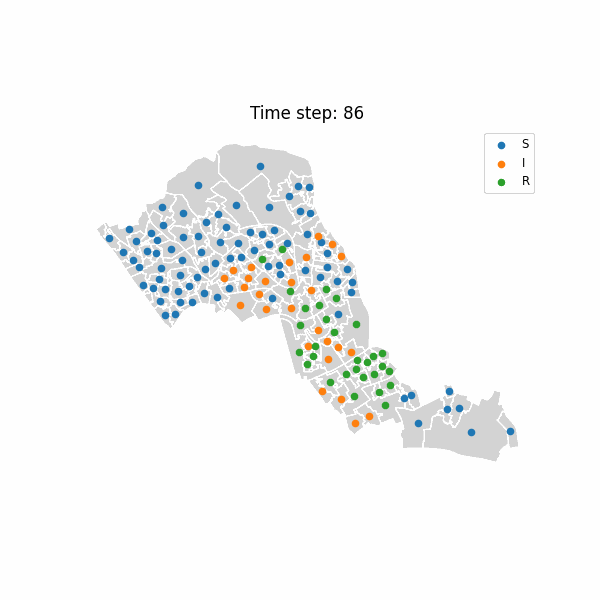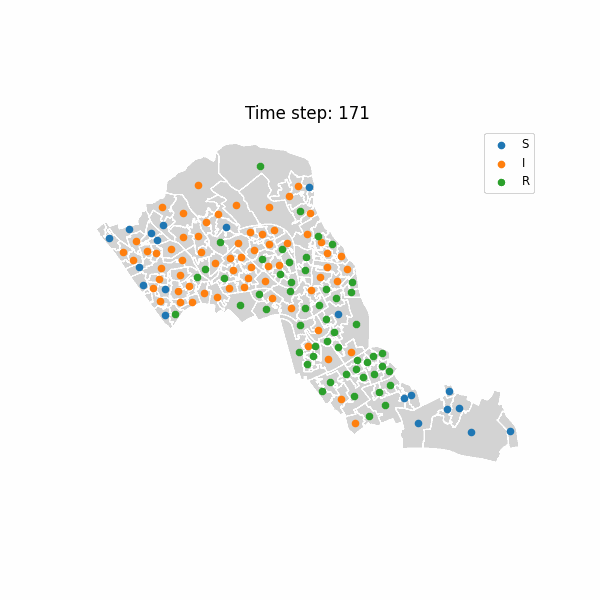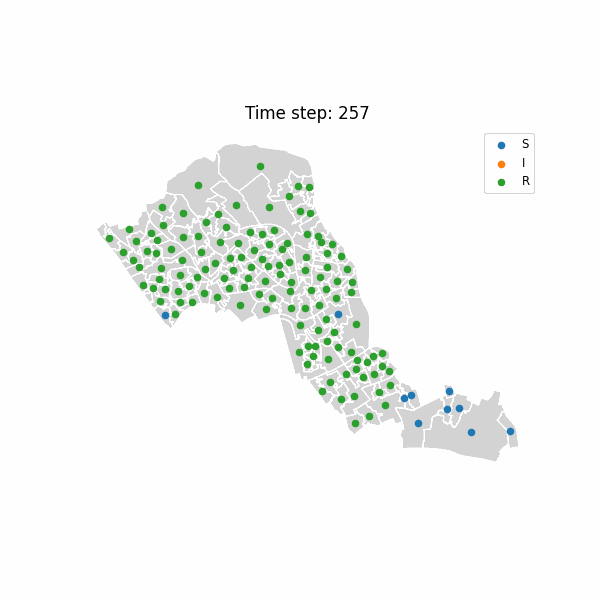

 

当我们播放这个动画时，可以看到红色的感染区域如何从一个点开始，逐渐扩散到周围的蓝色易感区域，然后变成绿色的康复区域。这种时空动态直观地展示了空间邻近性如何影响疾病的传播模式 🌍→🦠→💊。

模型的局限性与改进方向

尽管我们的空间 SIR 模型比传统模型更贴近现实，但它仍然有一些局限性：

1. 空间权重的简化：我们使用了简单的二元邻接矩阵来表示空间关系，而现实中的疾病传播可能受到多种因素影响，如人口流动、交通网络等。

2. 同质性假设：模型假设每个区域的人口特征是相同的，而实际上不同区域的人口密度、年龄结构等可能差异很大。

3. 确定性参数：我们使用了固定的感染率和康复率，而在现实中这些参数可能随时间和空间变化。

针对这些局限性，我们可以考虑以下改进方向：

1. 更复杂的空间权重：可以基于实际交通数据或人口流动数据构建更真实的空间权重矩阵。

2. 异质性建模：可以为不同区域设置不同的人口特征和疾病传播参数。

3. 引入行为干预：可以模拟社交距离、封锁等干预措施对疾病传播的影响 🛡️。

4. 考虑人口流动：可以引入更复杂的人口流动模型，模拟通勤等日常活动对疾病传播的影响。

结语：空间视角下的传染病防控

通过这个案例，我们看到了地理空间视角在传染病建模中的重要性。空间邻近性、区域连接性等因素显著影响着疾病的传播模式和速度。在公共卫生政策制定中，考虑这些空间因素可以帮助我们更精准地分配资源、实施干预措施。

想象一下，当我们能够在地图上实时看到疾病的传播路径和高风险区域时，公共卫生部门就可以更有针对性地部署医疗资源、实施隔离措施，从而最大限度地减少疾病的影响 🏥。

这个模型不仅是一个学术研究工具，也为我们理解现实世界中的传染病传播提供了一个窗口。随着地理信息技术和计算能力的不断发展，我们有理由相信，未来的传染病模型将更加精确、更加贴近现实，为全球公共卫生安全提供更强有力的支持 🌟。

如果你对这个模型感兴趣，不妨尝试调整参数看看会发生什么变化：增加或减少感染率 β，看看疾病传播速度如何变化；调整空间权重的阈值，看看空间网络结构如何影响传播模式。探索不同场景下的疾病传播动态，也许你会有新的发现哦！ 🧪

完整代码（省流版）

import random
import numpy as np
import pandas as pd
import geopandas as gpd
import libpysal
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation, PillowWriter# Reproducibility
random.seed(33333334)
np.random.seed(33333334)# Load shapefiles for City of London and Camden
lon = gpd.read_file("LSOA_2011_BFE_City_of_London.shp")
cam = gpd.read_file("LSOA_2011_BFE_Camden.shp")
# Combine GeoDataFrames
df = pd.concat([lon, cam], ignore_index=True)# Keep a WGS84 copy for plotting maps in lon/lat
df_ll = df.to_crs(epsg=4326)# Re-project to a metric CRS before centroid calculations (EPSG:3857)
df = df_ll.to_crs(epsg=3857)# Compute centroids in both CRS
centroids_3857 = df.geometry.centroid
coords_3857 = np.vstack([centroids_3857.x, centroids_3857.y]).T
centroids_ll = df_ll.geometry.centroid
coords_ll = np.vstack([centroids_ll.x, centroids_ll.y]).T# Build spatial weights using Queen contiguity
w = libpysal.weights.Queen.from_dataframe(df, use_index=True)# Convert to weight matrix
n = len(df)
W = np.zeros((n, n), dtype=int)
for i, neighbors in w.neighbors.items():for j in neighbors:W[i, j] = 1W[j, i] = 1  # symmetric# Plot base map and centroids
plt.figure(figsize=(6, 6))
df_ll.plot(facecolor='none', edgecolor='black')
plt.scatter(coords_ll[:, 0], coords_ll[:, 1], s=10)
plt.title('Polygons and Centroids (WGS84)')
plt.show()# Histogram of positive weights
dist = W[W > 0]
plt.figure()
plt.hist(dist, bins=20)
plt.title('Distribution of Weights > 0')
plt.show()# Threshold adjacency
threshold = 0.16
adj = (W > threshold).astype(int)# Plot edges above threshold
g_df = df_ll.copy()
plt.figure(figsize=(6, 6))
g_df.plot(facecolor='none', edgecolor='gray')
plt.scatter(coords_ll[:, 0], coords_ll[:, 1], s=10, color='black')
for i in range(n):for j in range(i + 1, n):if adj[i, j]:plt.plot([coords_ll[i, 0], coords_ll[j, 0]],[coords_ll[i, 1], coords_ll[j, 1]],color='blue', linewidth=0.5)
plt.title('Network Edges (thresholded)')
plt.show()# SIR parameters
beta = 3.0
gamma = 1.0# Initialize status: 'S', 'I', 'R'
status = np.array(['S'] * n)
i0 = random.randrange(n)
status[i0] = 'I'# Storage
T_max = 10.0
times = [0.0]
states = [status.copy()]
adj_list = {i: list(np.where(adj[i] == 1)[0]) for i in range(n)}
current_time = 0.0# Gillespie simulation
i = 0
while current_time < T_max:I_indices = np.where(status == 'I')[0]rec_rates = {idx: gamma for idx in I_indices}S_indices = np.where(status == 'S')[0]inf_rates = {idx: beta * sum(status[j] == 'I' for j in adj_list[idx]) for idx in S_indices}all_rates = {**rec_rates, **inf_rates}total_rate = sum(all_rates.values())if total_rate <= 0:breaknodes, rates = zip(*all_rates.items())probs = np.array(rates) / total_rateevent_node = np.random.choice(nodes, p=probs)if status[event_node] == 'S':status[event_node] = 'I'else:status[event_node] = 'R'dt = np.random.exponential(1.0 / total_rate)current_time += dttimes.append(current_time)states.append(status.copy())i += 1# Time series DataFrame
df_counts = [{'time': t,'S': int((st == 'S').sum()),'I': int((st == 'I').sum()),'R': int((st == 'R').sum())}for t, st in zip(times, states)]
df_ts = pd.DataFrame(df_counts)plt.figure()
for compartment in ['S', 'I', 'R']:plt.plot(df_ts['time'], df_ts[compartment], label=compartment)
plt.xlabel('Time')
plt.ylabel('Count')
plt.legend()
plt.title('SIR Dynamics Over Time')
plt.show()# Prepare DataFrame for animation
records = []
for step, st in enumerate(states):for idx, s in enumerate(st):records.append({'time_step': step,'node': idx,'status': s,'x': coords_ll[idx, 0],'y': coords_ll[idx, 1]})
anim_df = pd.DataFrame(records)# Animate with PillowWriter
def animate_sir_map(output_file='london.gif', fps=5):fig, ax = plt.subplots(figsize=(6, 6))def update(frame):ax.clear()df_ll.plot(ax=ax, facecolor='lightgray', edgecolor='white')df_step = anim_df[anim_df['time_step'] == frame]for label, color in zip(['S', 'I', 'R'], ['blue', 'red', 'green']):sub = df_step[df_step['status'] == label]ax.scatter(sub['x'], sub['y'], label=label, s=20)ax.set_title(f"Time step: {frame}")ax.legend(loc='upper right', fontsize='small')ax.set_axis_off()writer = PillowWriter(fps=fps)anim = FuncAnimation(fig, update, frames=len(states), interval=200)anim.save(output_file, writer=writer)print(f"Animation saved as {output_file} using PillowWriter")animate_sir_map()