（题目向，随时更新）动态规划算法专题(2) --见识常见的尝试模型

        经过上篇文章的介绍，相信朋友们已经对一道递归的题目，如何采用记忆化搜索来优化空间复杂度，又如何利用引入表结构的思想演化成严格位置依赖的动态规划，最后到一道动态规划题目如何利用滚动数组优化空间有了自己的理解和认识。上篇文章只是通过斐波那契数这样最简单的题目来揭示这个过程，别担心，跟着我，难题好题管够(doge)！从这篇文章开始，我们将大量介入题目实战，分析各种各样经典的，新颖的尝试模型。部分题目会从递归-记忆化搜索-严格位置依赖的动态规划-滚动数组优化整个过程进行一遍梳理，其余题目将着重以尝试模型为重点，只梳理DP解法。同时声明，这篇文章也是我通过学习左程云老师课程笔记的一个复现，旨在进行记录。基于个人刷题习惯，还是采用C++来进行代码的演示，不过在算法学习中语言并没有本质区别。

一维动态规划：

leetcode 983 最低票价 --区间尝试模型+映射构建

         题目描述请看链接。从题目中的信息我们可以提取出这个要点：有三种不同时效(1天，7天，30天)的通行证，对应不同的价格（入参1）。请注意，这个“三种”很重要，也是我个人认为本题目的一个特点，因为由此可以构建出一个定长的cost数组。这里补充一点解题的技巧，如果第一遍看题目描述迷迷糊糊不太明白这是正常现象，不要慌，看看给出的测试用例，对应好入参和出参，代入着再读一遍题目，也许就好理解多了！接下来给出了一个数组days（入参2）代表你在哪些天需要旅行。这里我需要先阐明一点，通行证是本日买次日用的，否则容易陷入理解误区。最终题目要你返回最低的消费。

        首先，如果我们从递归的角度来思考这道题目，那么我们必须清楚递归的含义以及Basecase是什么。探寻递归的含义，大忌就是瞻前顾后，最好的办法永远是选择一个最一般的位置，以结果为导向，看看什么时候这条路“走到头了”，而这个尽头就很大概率是我们常说的Basecase。对于这道题目来说，我们以日期(数组days)作为讨论的出发点，讨论从第i天开始出发到第n天的最低消费。这便是我们这道题的递归含义f(i)，我们需要拿到的结果是从第0天到第n天的最低消费，也就是f(0)。接下来题目中告诉我们这个days数组是有范围的（1~365天），那咱们就假设的极端点来看：如果我在最后一天出发旅行，那还买什么通行证啊，根本没有时间能去旅游了，更不会有开销！假设days数组的长度为n，则当i=n时，最低消费为0！这也就是本题目的Basecase。接下来我们来看从最一般的i位置，具体会发生什么样的事情，这便是尝试模型的讨论。

        我们在这里做一个假设：假设时效为1天，7天，30天的通行证价格分别为2元，7元，15元。而这个价格被整理为数组当作入参，所以我们要构建一个“时效-价格”的映射。即duration数组{1,7,30}，通过数组下标位置的对应来实现这个映射。在当前i位置，我们如何决定使用哪种方案消费最低呢？不难发现，如果非要买一张通行证，可能性只有三种，或者压根不买，关键是什么情况不买呢？如果当前通行证仍能生效，我为什么要买呢，屯着吗？及时行乐不香吗！既然只有这么少的可能性，简单粗暴的枚举想必不会有多大的开销！我们只需要在枚举的过程中取最小值即可。在枚举最小值的时候我们要注意边界要求。由此这道题目的尝试模型也便整理出来了，我们可以写出这道题目的递归解法。

class Solution {
public:vector<int> duration={1,7,30};int f(vector<int>& days, vector<int>& costs,int i){//递归Basecaseif(i==days.size()){return 0;}//由于存在比较逻辑，求的又是最小值，所以答案初始化系统最大int ans=INT_MAX;//枚举可能性for(int k=0,j=i;k<3;k++){//如果当前通行证还能生效，那我肯定不买while(j<days.size()&&days[j] < days[i] + duration[k]){j++;}//比较逻辑ans=min(ans,costs[k]+f(days,costs,j));}return ans;}int mincostTickets(vector<int>& days, vector<int>& costs) {return f(days, costs,0);}
};

        当你满心欢喜的写完这段代码，兴致勃勃的正准备提交，我劝你先等等，冷静一下，不要被眼前的“胜利”冲昏了头脑，别问我是为什么知道的~好了，不卖关子了，如果这样执行的话会导致超时。那怎么优化空间呢？挂个傻缓存降低查询次数不就结了？于是我们引出记忆化搜索的方法：

class Solution {
public:vector<int> duration={1,7,30};int f(vector<int>& days, vector<int>& costs,vector<int>& dp,int i){if(i==days.size()){return 0;}if(dp[i]!=INT_MAX){return dp[i];}int ans=INT_MAX;for(int k=0,j=i;k<3;k++){while(j<days.size()&&days[j] < days[i] + duration[k]){j++;}ans=min(ans,costs[k]+f(days,costs,dp,j));}dp[i]=ans;return ans;}int mincostTickets(vector<int>& days, vector<int>& costs) {//缓存表vector<int> dp(days.size());for(int i=0;i<days.size();i++){dp[i]=INT_MAX;}return f(days, costs,dp,0);}
};

        爽了爽了，但是也请你先从AC的快感中慢慢冷静下来，我们为何不能更进一步呢！我们来看递归函数，传入的四个参数分别是days,costs,dp数组和i位置，不难发现只有i唯一一个可变参数可以完全决定返回值！所以这妥妥一道一维动态规划。上面整理的尝试模型（依赖关系）完全可以整理在一张线性表结构中。从前面递归的求解中我们不难看出，我们的Basecase位置是dp[n]，目标位置是dp[0]，也就是说我们这道题的动态规划表是从右向左填的！这个决定了填dp表时的循环控制逻辑。由以上分析我们可以很容易得到下面的dp版本解法：

class Solution {
public:vector<int> duration = {1, 7, 30};int mincostTickets(vector<int>& days, vector<int>& costs) {int n = days.size();vector<int> dp(n + 1, INT_MAX);  // dp[i] 表示从 days[i] 开始的最小花费dp[n] = 0;  // 最后一天之后的花费为 0// 自底向上计算 dpfor (int i = n - 1; i >= 0; i--) {for (int k = 0, j = i; k < 3; k++) {while (j < n && days[j] < days[i] + duration[k]) {j++;}dp[i] = min(dp[i], costs[k] + dp[j]);}}return dp[0];}
};

二维动态规划：

leetcode 1143 最长公共子序列--区间尝试模型

         题目描述请看链接。本来想把子序列，子数组问题全部都归结到一个专题里来作为介绍，但是奈何这道题实在太过经典，忍不住放在本文中直接向大家介绍了。不过接下来也会更新子数组，子序列相关的专题，这里先挖个坑后续会填。给定了两个字符串text1和text2（两个入参），返回最长公共子序列的长度。

        首先我们需要区分一个很重要的概念，因为这直接关系到对于这道题目的理解。我们必须区分子数组和子序列的区别：子数组必须是连续的，而子序列可以不连续。鉴于这道题确实比较抽象，我们来举个实例来介绍这道题目，请看下图：

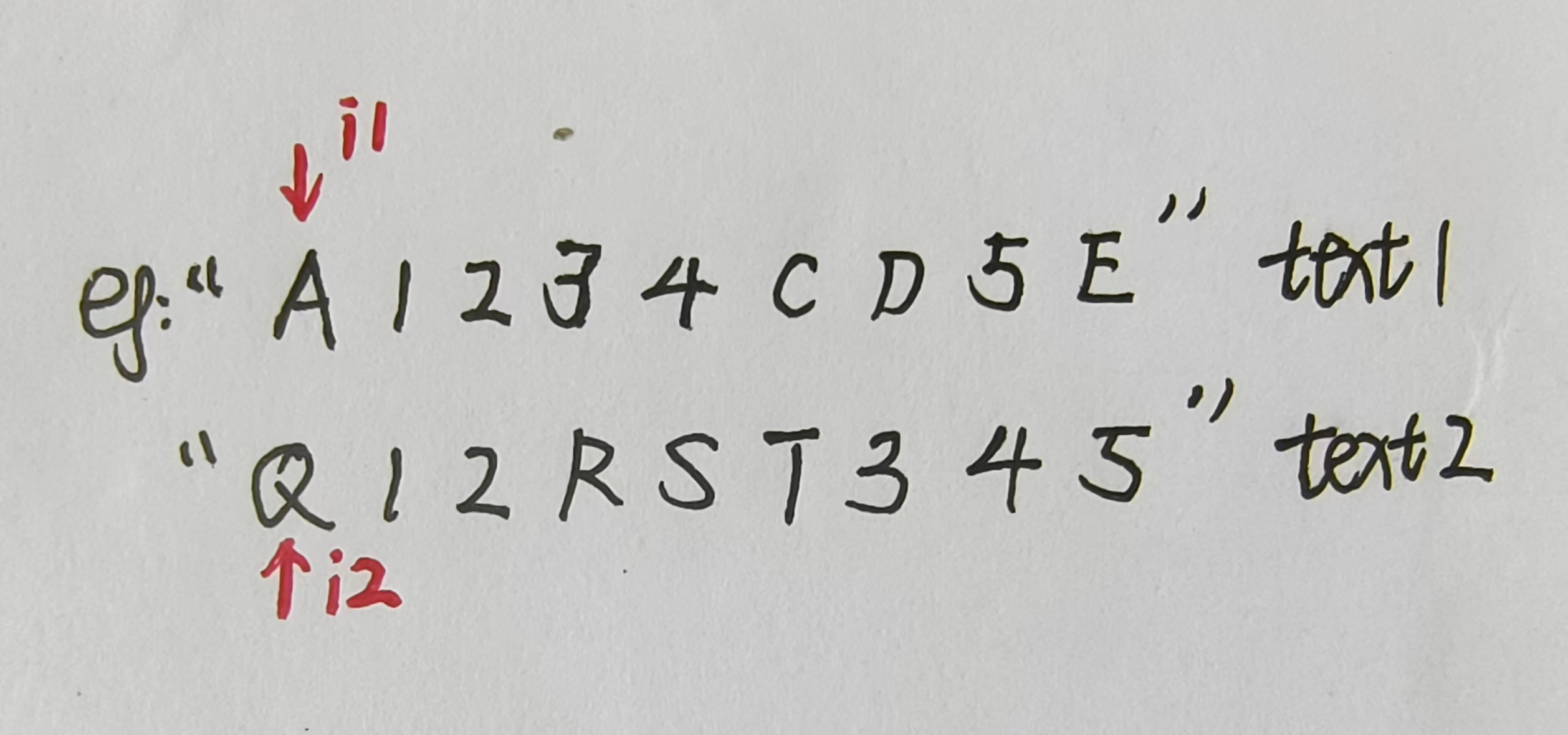
        由上图我们很容易看出text1和text2的最长公共子序列为"12345" ，长度为5。之前介绍过，在探索尝试模型的时候，通常是以结果为导向的。我们要求的是最长公共子序列的长度，我们的递归函数f的返回值就应该是这个长度（int整型值）。接下来我们分别需要i1,i2两个变量来标识text1,text2的位置，并针对这些位置进行讨论。当i1,i2处于最一般的位置时，f（i1,i2）代表的就是在text1，text2中分别以i1，i2为结尾的最长公共子序列的长度。假设text1串长度为n，text2长度为m，我们要求的最终答案就是f(n,m)。当i1或者i2为负值，这纯粹是捣蛋，直接返回0，这就是这道题目的Basecase。接下来讨论最一般的以i1,i2为两串结尾的情况，为了达到子序列长度最长的目的，有四种可能情况需要考虑：即i1和i2位置所代表的字符都不要，只要i1位置对应的字符，只要i2位置对应的字符和两者都要。

        如果i1和i2位置代表的字符都不要，那么也就意味着原来的字符串无法通过分别加上i1,i2位置的字符达到延长公共子序列长度的目的，我们便讨论以i1-1,i2-1位置为结尾的字符串中最长公共子序列的长度f(i1-1,i2-1)；如果i1位置处的字符不要，而要i2位置处的字符，我们便讨论以i1-1,i2位置为结尾的字符串中最长公共子序列的长度f(i1-1,i2)；要i1而不要i2同理(f(i1,i2-1))。最后如果我们同时要i1和i2位置的字符时，如果text1[i1]=text2[i2]，则发现了公共部分，最长公共子序列长度+1！如果不相同则返回0，我们在这四种可能性之间取最大值即可。通过上述分析我们可以很容易的整理出下面的递归解法，不过别高兴的太早，因为还是超时！

class Solution {
public:int f(string s1,string s2,int i,int j){if(i<0||j<0){return 0;}int p1=f(s1,s2,i-1,j-1);int p2=f(s1,s2,i,j-1);int p3=f(s1,s2,i-1,j);int p4=s1[i]==s2[j]?(p1+1):0;return max(max(p1,p2),max(p3,p4));}int longestCommonSubsequence(string text1, string text2) {int n=text1.size();int m=text2.size();return f(text1,text2,n-1,m-1); }
};

        现在理清楚了思路，那就接着往下干呗！别急，我们不妨换个思路，一题多解才能更有助于我们的思维扩展。在大多数子数组/子序列问题中，我们可以根据是否要结尾处的字符来进行讨论。同时，我们还可以根据字符串的长度进行讨论，其实和前一种方法原理上是大同小异的。拿这道题目来说，递归函数f的含义就变成了在text1，text2中长度分别为len1,len2的子串构成的最长公共子序列的长度。情况的讨论大同小异，此处便不再赘述，由此按照上篇文章所介绍的方法，挂个傻缓存，就能得到记忆化搜索的版本了：

class Solution {
public:int f(string s1, string s2, int len1, int len2, vector<vector<int>>& dp) {if (len1 == 0 || len2 == 0) {return 0;}if (dp[len1][len2] != -1) {return dp[len1][len2];}int ans = 0;if (s1[len1 - 1] == s2[len2 - 1]) {ans = f(s1, s2, len1 - 1, len2 - 1, dp) + 1;} else {ans = max(f(s1, s2, len1, len2 - 1, dp), f(s1, s2, len1 - 1, len2, dp));}dp[len1][len2] = ans;return ans;}int longestCommonSubsequence(string text1, string text2) {int n = text1.size();int m = text2.size();vector<vector<int>> dp(n + 1, vector<int>(m + 1, -1));return f(text1, text2, n, m, dp);}
};

        接下来重头戏来了：我们如何整理上面的这些依赖关系，通过迭代更新动态规划表来解决这个问题而不是采用传统的递归方式。首先在这道题目中，通过看上面的递归函数我们不难发现只有len1,len2两个可变参数完全决定了递归函数的返回值，所以这是一道二维动态规划题目，需要用一张二维表来整理依赖关系。还有，我们并不知道这张动态规划表开多大(两串的长度是传入的参数，不确定)。我们在填写动态规划表时，先讨论最特殊的取值，找到目标点，再从任意一个一般格子出发来整理依赖关系。可能看我这段描述会感到云里雾里，没关系，我们结合下面这张图来完整讲述填表的过程！

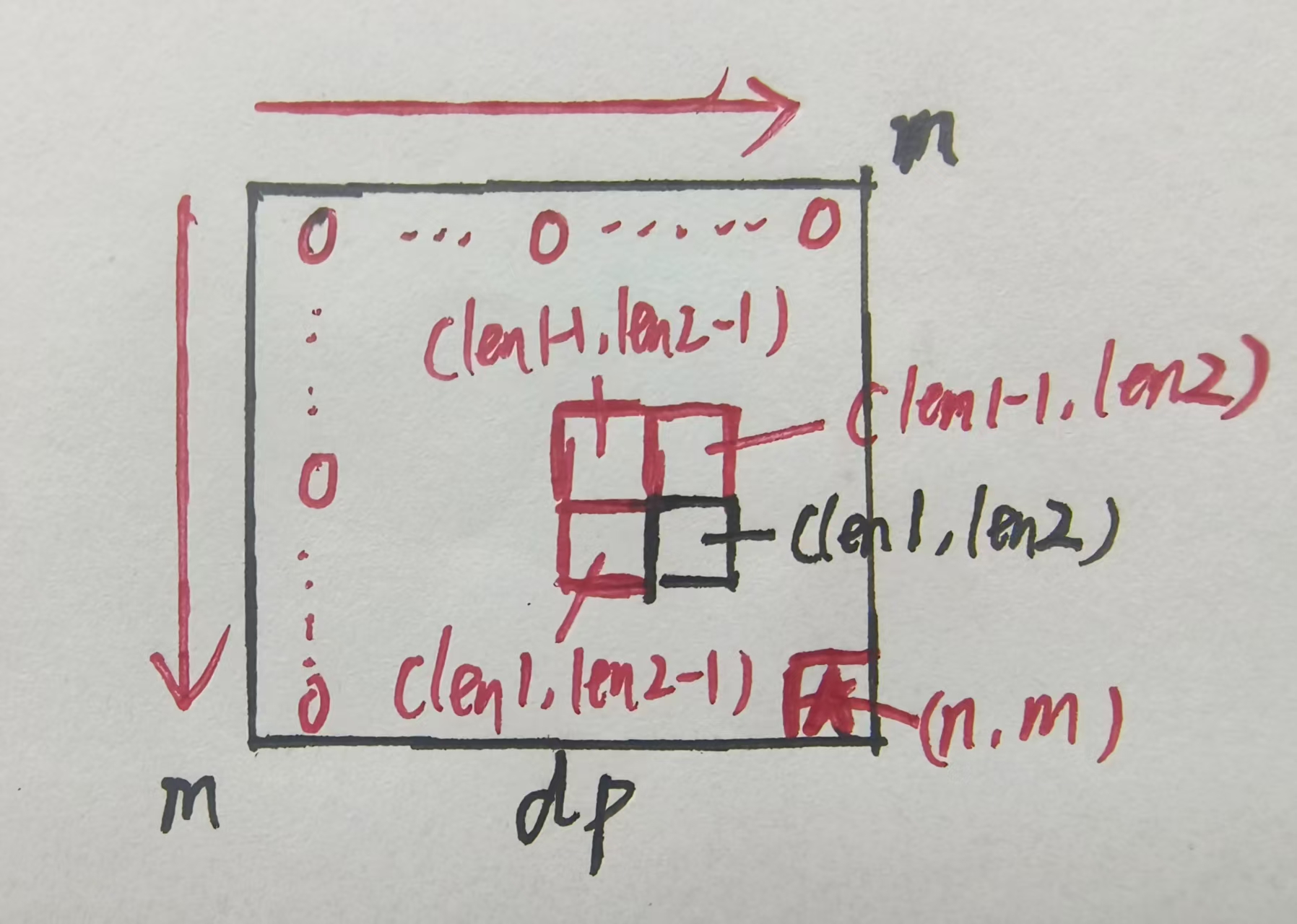
        首先，当len1或者len2为0的时候，长度都为0了，那最长公共子序列的长度肯定也就是0了，所以dp表的第0行和第0列全部填0。当len1=n,len2=m，代表的是text1,text2整个字符串范围上的最长公共子序列的长度，也就是我们所求（表中五角星标出的(n,m)位置），即为这个动态规划表中的目标点。接下来我们取出一个最一般的位置(len1,len2) ，结合上面整理的依赖关系，我们不难发现(len1,len2)位置的值依赖于(len1-1,len2-1),(len1,len2-1),(len1-1,len2)这三个方向的格子(图中以标红)，红色箭头标出了迭代的方向，由此我们便可以填写完这张dp表并且获得结果：

class Solution {
public:int longestCommonSubsequence(string text1, string text2) {int n = text1.size();int m = text2.size();vector<vector<int>> dp(n + 1, vector<int>(m + 1));for(int len1=1;len1<=n;len1++){for(int len2=1;len2<=m;len2++){if(text1[len1-1]==text2[len2-1]){dp[len1][len2]=1+dp[len1-1][len2-1];}else{dp[len1][len2]=max(dp[len1-1][len2],dp[len1][len2-1]);}  }}return dp[n][m];}
};

        以上便是本篇文章的全部内容了。选取比较经典的题目来介绍经典的尝试模型，通过大量刷题建立题感。本篇文章会持续更新，加入新的题目，带大家获取更多的新灵感，还请大家多多关注和支持，我们一起成长！